基于能量原理的岩爆倾向性判据

孙飞跃，范俊奇，郭佳奇,3，石晓燕，刘希亮,3，朱斌忠，张恒源

（1.河南理工大学土木工程学院，河南 焦作 454000；2.军事科学院国防工程研究院，河南 洛阳 471023；3.河南省地下工程与灾变防控重点实验室，河南 焦作 454000）

岩爆是地下工程开挖过程中，积聚的弹性变形能瞬间释放而产生突然爆裂的动力失稳现象，常伴有岩石弹射或抛出、强烈震动、巨大的声响和气浪等现象[1]。自1738年英国South Stafford 锡矿发生首次岩爆以来，世界范围内已有南非、印度、日本、中国以及欧美等国家和地区相继发生过岩爆[2–4]。岩爆具有很强的突发性、局部性、隐蔽性和危害性，极大地威胁着现场施工人员和设备的安全，同时给深地工程设计和施工安全带来了严重挑战[5]。因此，确切认清岩爆发生机制、准确掌握岩爆孕育演化规律以及岩爆发生的可能性、精准预测岩爆活动的强弱，是目前亟待开展的工作。

迄今为止，国内外岩石力学工作者和工程技术人员以深部岩体力学和非线性动力科学理论为指导，从理论分析、数值模拟、现场监测以及试验等方面，针对岩爆判据与岩爆分级开展了深入研究，并基于各自的假设提出了相应的预测评价指标。在岩爆判据与岩爆分级理论研究方面，国内外专家学者从不同角度相继提出了数十种经典岩爆判据和烈度分级，如E. Hoek 判据、Russenes判据、Turchaninov 判据、Kidybinski 能量判据、Motycaka 能量比法、Barton 判据、二郎山公路隧道判据以及谷-陶判据等[6–13]。在现场监测研究方面，学者们开展了大量工作，取得了一些卓有成效的研究成果，如微震监测法、声发射监测法、微重力法、声波探测法、红外热像法等[14–18]。在岩爆判据的试验和数值模拟方面，岩石工程领域的专家与学者也开展了深入、系统的研究工作，并取得了长足进展。吴枋胤等[19]基于现场岩样点荷载试验，提出了岩爆烈度分级，并成功应用于拉林铁路典型岩爆隧道工程。李子运等[20]开展了页岩在不同围压作用下的三轴循环荷载试验研究，提出了基于能量突变的岩石强度失效判据。杨凡杰等[21]通过室内试验对岩体裂纹动态扩展问题进行了研究，提出了一个新的岩爆能量判别指标，并将该指标成功应用于实际工程案例模拟中。李夕兵等[22]针对深部硬岩矿山岩爆的动静组合力学机制问题，综合采用室内试验与数值模拟相结合的方法，提出了基于动静能量指数的岩爆动力判据。Gong 等[23]提出了一种基于室内试验测试岩石试样破坏结果和现象的岩爆倾向性分级标准。Karchevsky[24]通过试验研究提出了一种计算数量算法，并将该算法作为判别煤层中岩石发生破裂可能性的标准。随着计算机技术的快速发展，数值分析法应运而生并日趋完善，学者们基于能量理论提出了不同的岩爆判据数值指标，如能量释放率（Energy release rate，ERR）、超剪应力（Excessshear stress，ESS）、岩爆倾向指数（Burst potential index，BPI）、局部能量释放密度（Local energy release density，LERD）、局部能量释放率（Local energy releaserate，LERR）、相对能量释放指数（Relative energy releaseindex，RERI）、单位时间相对能量释放率（Unit time relative local energy release index，URLERI）等[25–31]。

上述成果极大地推动了岩爆判据研究的发展，但目前对于工程应用较广的岩爆能量判据（或指标）研究还鲜有文献报道，此外，岩爆发生的影响因素众多，而以上关于岩爆判据的研究仅考虑了其中一种或两种影响因素，导致其理论研究远落后于工程实践，且在工程适用性方面还存在不足。如果能够提出一套可准确反映岩爆孕育发生过程的多因素（力学因素、脆性因素、储能因素与完整性因素）岩爆能量判据，对深埋地下工程围岩的稳定性评价和安全施工将具有重要的指导意义。鉴于此，本研究在充分搜集、总结以及深入系统剖析国内外已有的岩爆判据与岩爆分级的基础上，试图建立一个基于能量原理的岩爆倾向性判据与岩爆分级模型，以期为岩爆的预测预报提供基本的科学依据和理论支持。

1 岩石受力变形过程的能量转化机制

岩石发生变形破坏主要是能量驱动的结果。从能量角度出发，当岩石在外力作用下产生变形，假设该物理过程与外界没有热交换，外力功产生的总输入能量为U，根据能量守恒原理得[32]

式中：Ud为岩石耗散能，用于形成材料内部损伤和塑性变形，如图1中曲线围成的空白区域所示；Ue为岩石可释放弹性应变能，如图1中曲线围成的阴影区域所示，表达式为

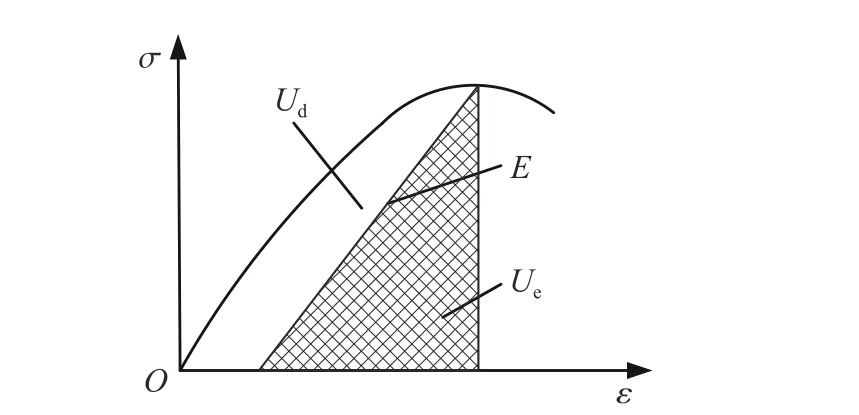
图1 岩石应力-应变关系曲线Fig.1 Stress-strain curve of rock

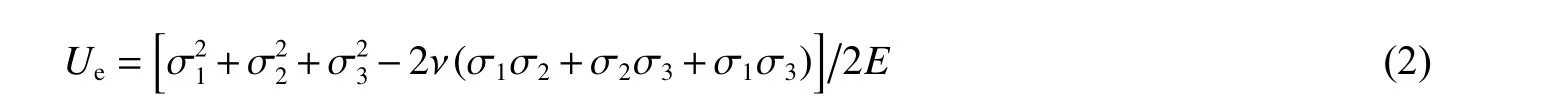
式中： σ1、σ2、σ3分 别为单元应变能最大值对应的3个主应力，E为弹性模量， ν为泊松比。

基于岩石受力变形过程中的能量转化对岩石动态与静态破坏的差别进行解释。由于受到动力荷载扰动产生的高应力作用，部分岩石单元体在极短时间内损伤加剧，强度逐渐降低，而大部分岩石储存的弹性应变能迅速达到极限值。当Ue达 到岩体破坏所需的能量U0，即Ue=U0时，Ue完全释放，岩体发生静态破坏；当Ue＞U0时，岩体发生动态破坏，能量差额∆U=Ue−U0构成分裂岩体的动能，诱发岩爆发生。

2 基于能量原理的岩爆判据

2.1 岩爆烈度分级

现有的岩爆工程案例表明，岩爆多发生于岩质中硬到坚硬、岩体完整性介于较好到完整性好之间、干燥、高地应力条件下的脆性岩体内。目前，地下工程岩爆判据主要考虑以下指标：洞室最大主应力 σ1、洞室最大切向应力 σθ、洞室径向应力 σr、岩石单轴抗压强度 σc、岩石抗拉强度 σt、岩石弹性能指数Wet、岩体完整性系数Kv及 侧压力系数 λ等。

通过对已有岩爆判据与岩爆等级进行深入剖析可知：（1）大部分岩爆判据以径向应力和切向应力或最大切向应力来表示，在使用数值模拟软件对地下工程开挖过程进行岩爆风险预测评估时，需进行坐标变换，因而应用相当繁琐[33–34]；（2）岩爆判据评价指标单一，或仅考虑其中一种或两种因素，如力学因素或脆性因素等，未全面考虑岩爆影响因素；（3）由岩爆定义可知，围岩应力是诱发岩爆的必要条件之一[35]，且岩爆区围岩大多处于三向应力状态，但已有的岩爆判据多以最大主应力或最大切向应力及两向应力状态来表示；（4）岩爆等级大多分为3级（无、中等和强烈岩爆）或4级（无、轻微、中等和强烈岩爆），且采用的判别指标也存在差异。

2.2 岩爆倾向性判据的建立

建立基于能量原理的岩爆判据，首先需要厘清岩石变形与破坏过程中的能量演化规律。本研究以谢和平等[32]提出的岩石强度与整体破坏准则为基准，分别给出岩体单元受压与受拉时的岩爆倾向性判据（Rockburst proneness criteria，RPC）与岩爆分级。

2.2.1受压情况（σ1＞σ2＞σ3≥0，压应力为正）

大量地下工程实践表明，地下洞室开挖前，围岩体的应力状态多为三向受压，如图2(a)所示。岩体发生整体破坏时，在主应力σi(i=1,2,3)方向，弹性应变能与能量释放率成正比，并依据最小压应力差分配弹性应变能，假设能量释放率的表达式为

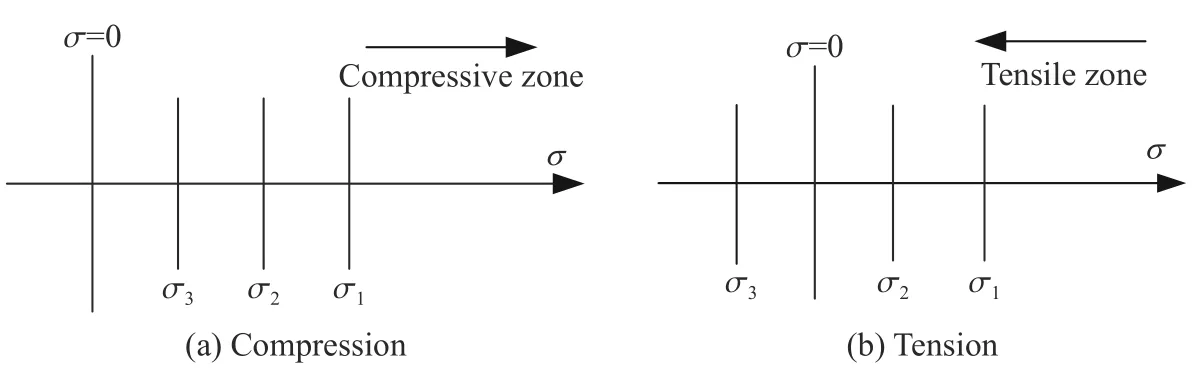
图2 受力情况[32]Fig.2 Loading cases[32]

式中：Gi为能量释放率，K为材料常数。

由式（3）可知，最大能量释放率发生在最小压应力 σ3方向，即

这也进一步说明静水压力状态不会导致岩体发生整体破坏。

由上述分析可知，岩体发生岩爆的能量释放率满足

式中：Gc为岩体在受压状态时的岩爆临界应变能释放率，为材料常数，可由室内岩石力学试验（单向压缩试验）确定。令σ1=σc， σ2=σ3=0，代入式（5），并联立式（2）可得

进一步考虑岩体完整性系数Kv对诱发岩爆的影响，联立式（3）～式（6），建立基于能量原理、岩体三向受压状态的岩爆倾向性判据Rc

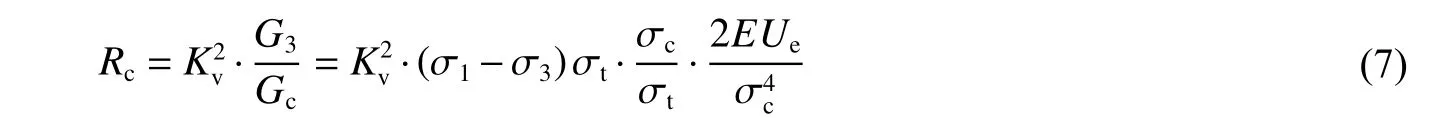
由式（7）可知：（1）基于能量原理的岩爆倾向性判据分析模型反映了岩爆孕育发生过程的完整性因素Kv、力学因素(σ1−σ3)σt、脆性因素σc/σt与储能因素Ue/σ4c；（2）该判据在数学表达形式上为主应力的乘积，便于理解、运用与操作；（3）该判据不仅考虑了围岩应力状态(σ1,σ2,σ3)与岩体完整性，还反映了岩石力学参数(σt,σc)与 变形参数(E,ν)的影响。

2.2.2受拉情况（σ3＜0）

地下工程开挖卸荷时，围岩体经常出现拉应力，这也是一种导致岩体发生整体破坏的应力状态。当岩石单元主应力至少出现一个拉应力（见图2(b)）、岩体发生整体破坏时，在主应力 σi方向的弹性应变能与能量释放率成正比，并依据主应力的大小来分配弹性应变能，假设能量释放率Gi的表达式为

类比受压情况，由式（8）可知，最大能量释放率发生在最大拉应力 σ3方向，即

岩体发生岩爆的能量释放率满足

式中：Gt为岩体在受拉状态的岩爆临界应变能释放率，为材料常数，可由室内岩石力学试验（单向拉伸试验）确定，令σ3=σt， σ1=σ2=0，代入式（10），并联立式（2）可得

进一步考虑岩体完整性系数Kv对诱发岩爆的影响，联立式（8）～式（11），建立基于能量原理、岩体受拉状态的岩爆倾向性判据Rt

类比受压情况，由式（12）可知，岩体在受拉状态时，岩爆倾向性判据也反映了岩爆孕育发生过程的完整性因素Kv、力学因素σ3/σc、 脆性因素 σc/σt与储能因素Ue/σ2t。

为确定基于能量原理的岩爆倾向性判据的界限值，在结合Zhang等[36]、尚彦军等[37]给出的弹性能指数界限值和岩爆势界限值划分的基础上，以表1所示的天台山隧道岩爆实测数据资料为模拟样本进行分析，所得结果如表2所示，其中：L为测点距离，Ku为变形脆性系数，σmax为围岩最大主应力，σc/σmax为围岩强度比。考虑到不同因素界限指标同时达到最大值的概率较小，为便于实际应用，岩爆判据R的界限指标取为2、11和110。因此，基于能量原理，并考虑围岩力学因素、脆性因素、储能因素与完整性因素的岩爆判据及烈度分级如下

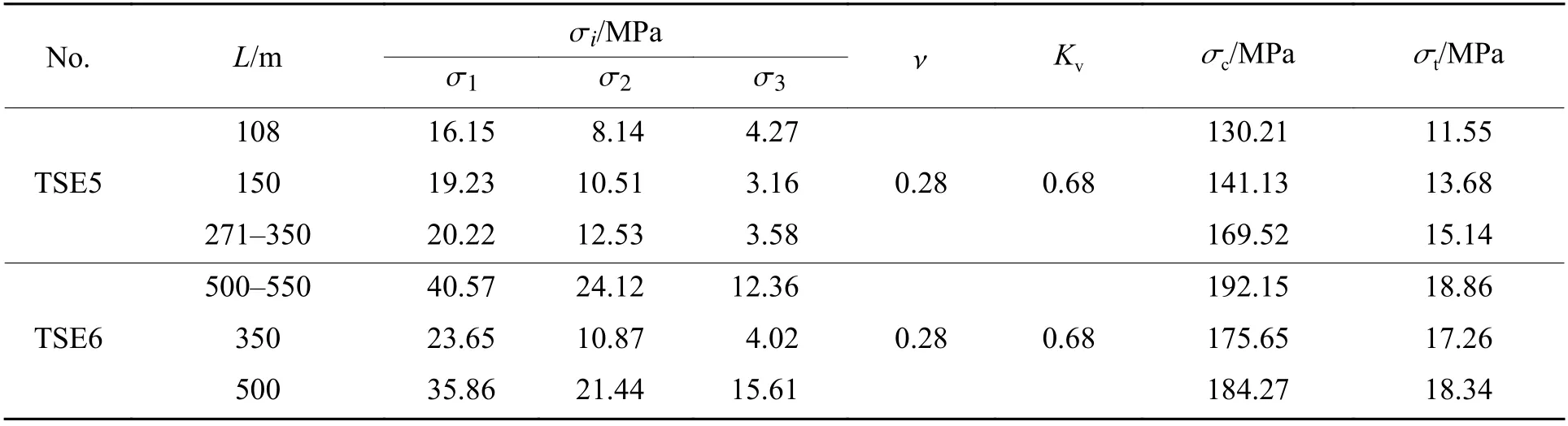
表1 天台山隧道岩爆实测数据[34]Table1 Measured data for rockburst at Tiantaishan tunnel[34]

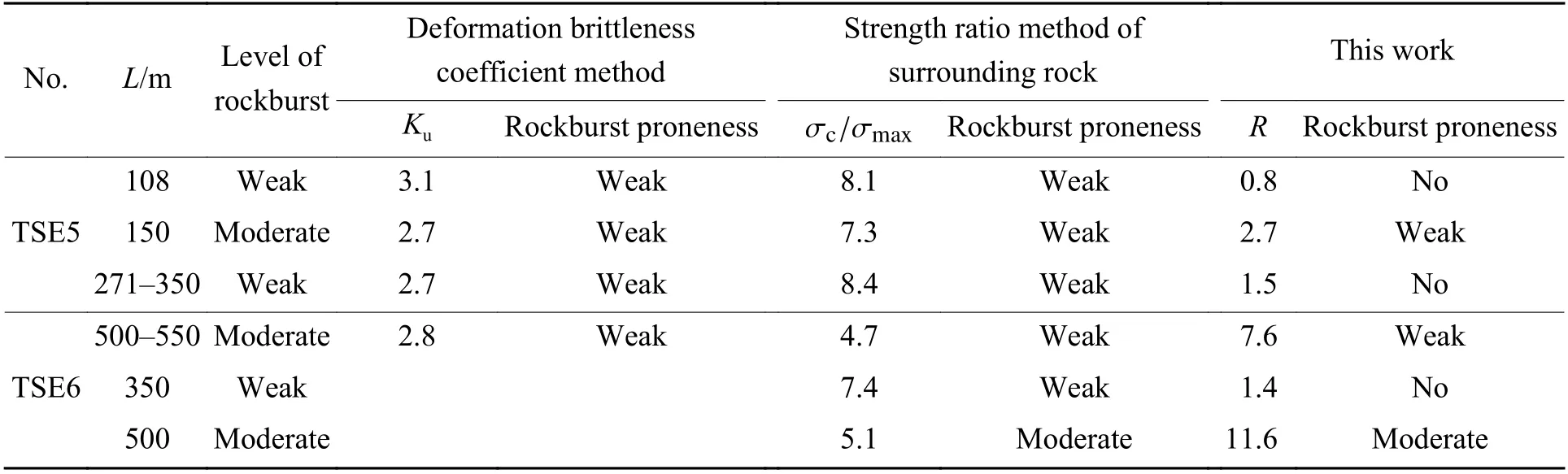
表2 天台山隧道模拟结果[34,38]Table 2 Simulated results for rockburst at Tiantaishan tunnel[34,38]

2.3 分析与评价

为进一步验证基于能量原理的岩爆倾向性判据的准确性、合理性、有效性以及可靠性，分别采用部分经典岩爆判据：E.Hoek 判据、Russenes判据、二郎山公路隧道判据、谷-陶判据以及本研究中提出的岩爆倾向性判据，对一些典型岩爆工程实例进行准确性和适用性检验，并与现场实际岩爆烈度等级进行对比分析，其中Ⅰ级表示少量片帮，Ⅱ级表示严重片帮，Ⅲ级表示需重型支护，Ⅳ级表示发生严重岩爆。分析结果如表3、图3及表4所示。其中 σ2、 σ3取值参照我国地应力分布规律[39]，并结合地应力测试成果而补充。

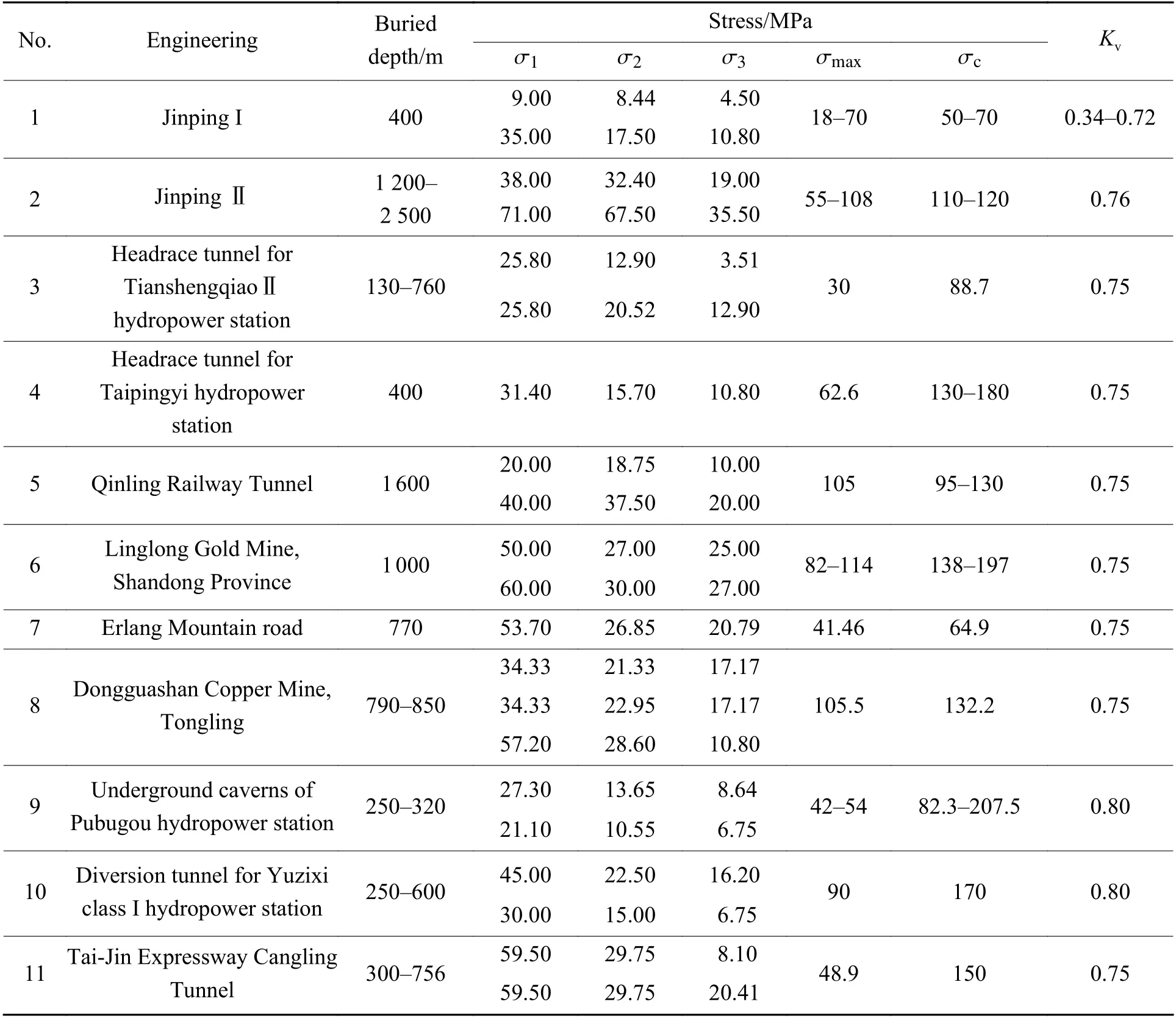
表3 工程岩爆分析初始数据[34,37]Table3 Initial data for rockburst analysis in someengineering[34,37]

（1）E.Hoek 判据

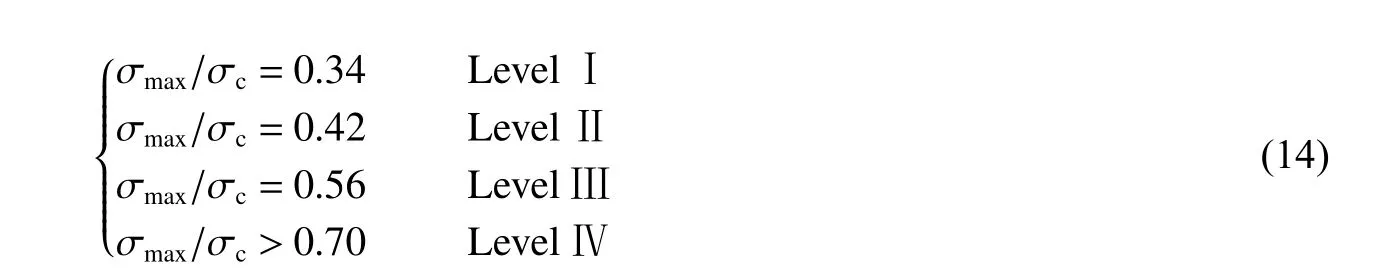
（2）Russenes判据

（3）二郎山公路隧道判据

徐林生和王兰生对Russenes判据进行了改进，得出以下岩爆判据

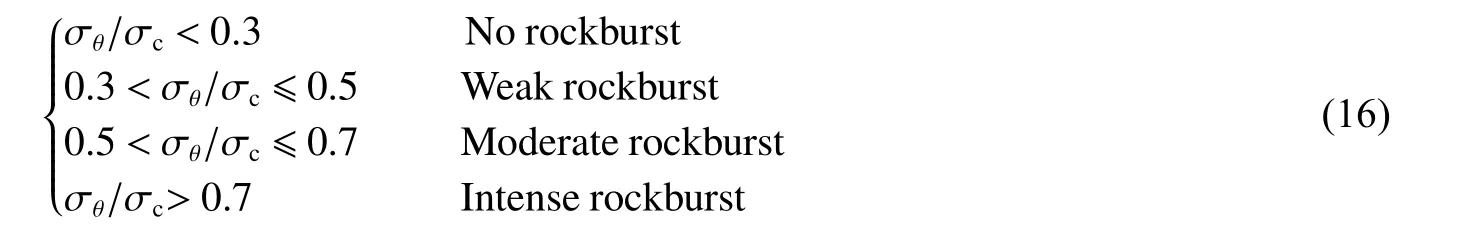
（4）谷-陶判据

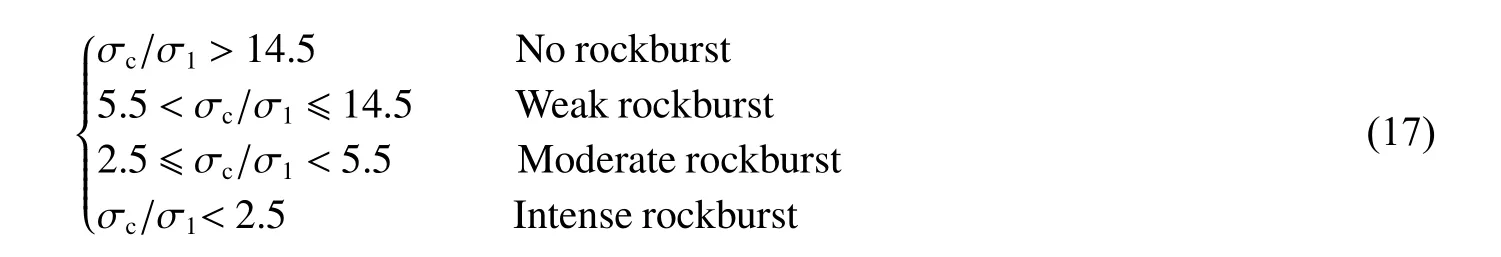
由图3和表4可知：（1）采用E.Hoek 判据、Russenes判据和二郎山公路隧道判据所判定的轻微、中等与强烈岩爆的总次数较接近，但E.Hoek 判据所判定的轻微岩爆次数略高于Russenes判据和二郎山公路隧道判据；（2）采用谷-陶判据所判定的岩爆等级主要集中在中等岩爆，轻微、强烈岩爆总次数较接近，说明其判定准确率略低于E.Hoek 判据、Russenes判据和二郎山公路隧道判据；（3）采用本研究提出的岩爆倾向性判据所判定的轻微、中等岩爆总次数与实际发生的轻微、中等岩爆总次数均接近，但其在强烈岩爆等级中的判定表现较弱。综合比较，本研究判据的正确判定次数与正确率明显高于其他4种判据，且总体上与岩爆发生实际情况基本一致，具有更好的有效性和工程适用性。

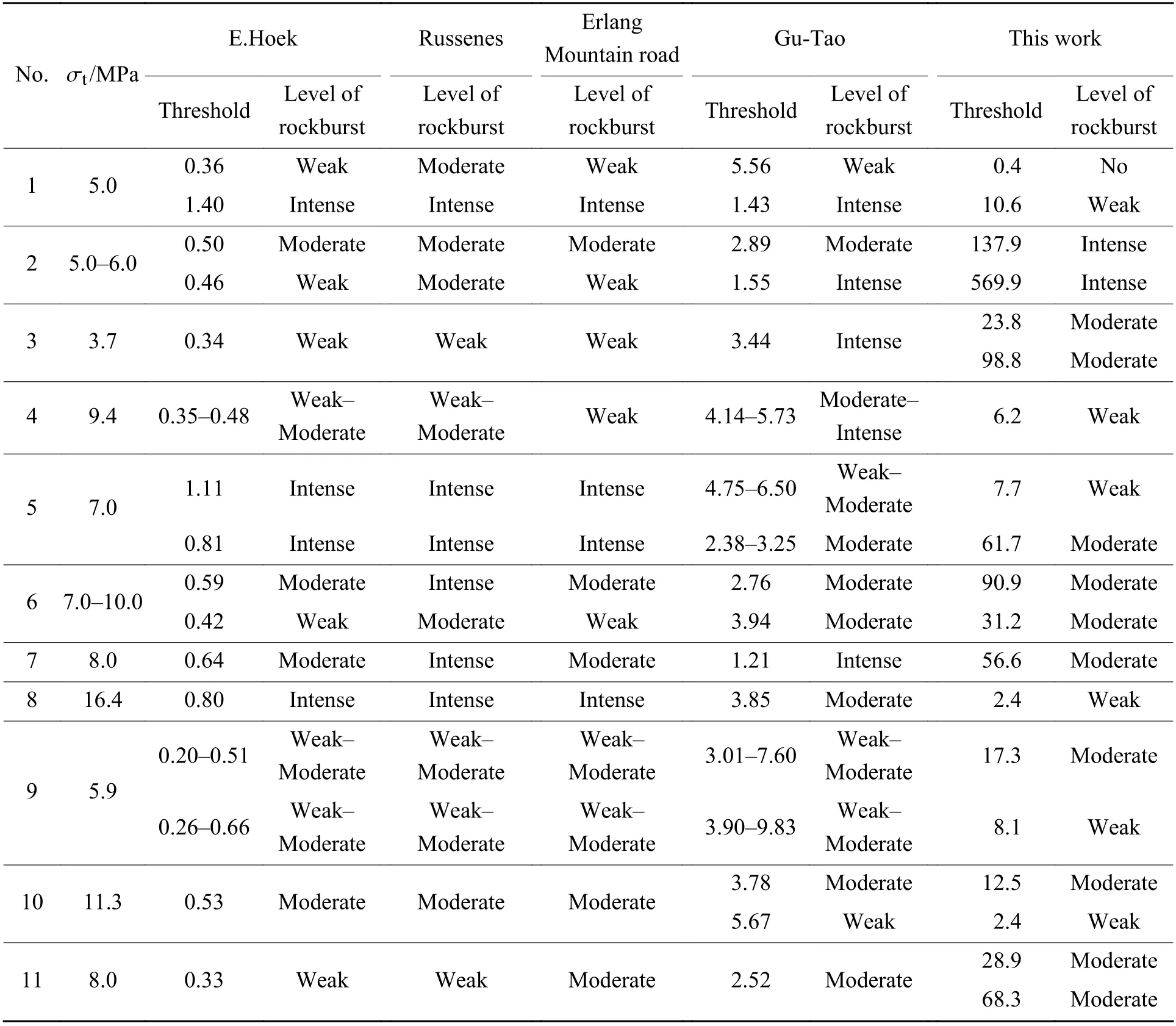
表4 典型岩爆实例预测结果验证[34]Table 4 Verification of prediction results of typical rockburst[34]

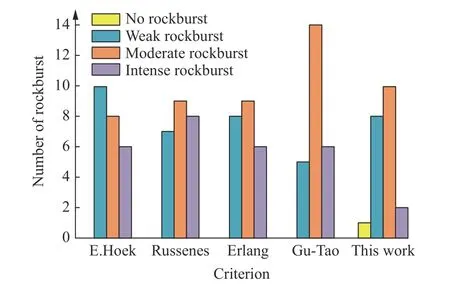
图3 不同岩爆判定结果对比[4]Fig.3 Comparison of rockburst results with different criteria[4]

由以上分析可知，本研究建立的岩爆倾向性判据意义明确，简单实用，能够较合理地定量判别深部地下工程施工过程中岩爆地质灾害的发生情况、烈度等级及位置范围。更重要的是，该判据全面考虑了围岩单元体受力的各种状态，反映了岩爆孕育发生过程的完整性因素、力学因素、脆性因素与储能因素，对岩爆预测评估更具有针对性和良好的工程适用性，对采用数值模拟软件进行深地下工程岩爆灾害的模拟预测分析具有十分重要的意义。

3 岩爆倾向性判据的数值分析

数值模拟方法已越来越广泛地应用于岩土工程研究领域，与现场或室内试验相比，数值模拟方法具有定量性、可重复性和经济性等优势，是理论分析或现场监测的有益补充和完善，同时若再辅以相关监测数据，则能较好地反映工程实际情况。

本节以锦屏Ⅱ级水电站4#引水隧洞为依托，通过三维离散元数值模拟软件3DEC对比验证岩爆过程数值模拟的可行性，并对本研究中提出的岩爆倾向性判据进行准确性和适用性检验；然后进行三维应力条件下深地下工程岩爆地质灾害孕育机理与演化规律数值模拟分析，研究深地下工程在开挖扰动作用下围岩的动态响应规律。

3.1 计算模型及边界约束条件

锦屏Ⅱ级水电站4#引水隧洞由东往西开挖，当开挖至K9+728标段时，K9+742～K9+766标段南侧边墙至拱脚部位发生了极强岩爆[40]（图4），岩爆坑深度大于2 m。通过现场勘查未发现此标段有控制性结构面，且围岩新鲜完整，该洞段围岩体主要为T2b大理岩，4#引水隧洞断面尺寸如图5所示。依据现场监测的地应力反演结果[40]，该洞段地应力水平较高，具体地应力状态见表5，其中： σx、 σy、 σz表示作用于x、y、z面且分别沿x、y、z方向的正应力， τxy、 τyz、 τzx表示作用于x、y、z面且分别沿y、z、x方向的切应力。

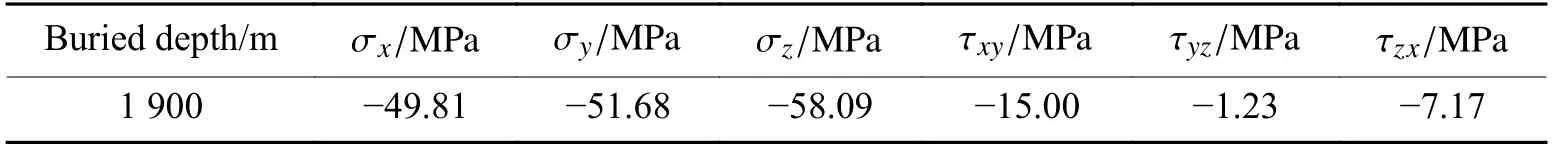
表5 4#引水隧洞岩爆段地应力状态Table5 In-situ stress state of rockburst section of 4# headracetunnel

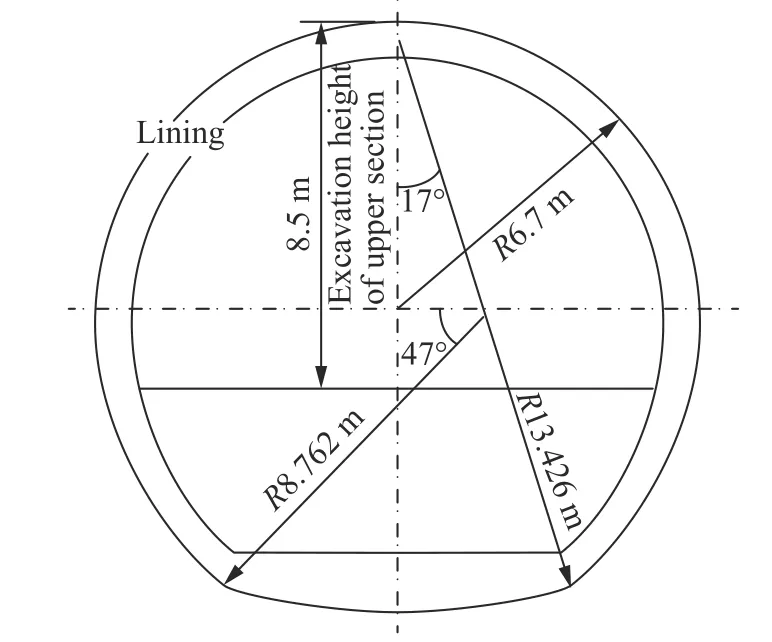
图5 4#引水隧洞断面尺寸[21]Fig.5 Dimension of 4# headrace tunnel[21]

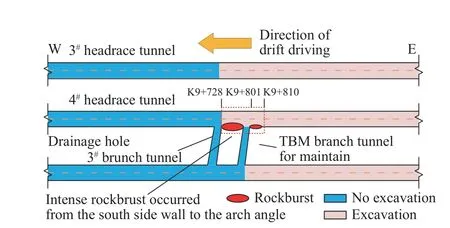
图 4 4#引水隧洞岩爆发生位置示意图Fig.4 Rockburst location of 4# headrace tunnel

采用三维离散元数值分析方法求解动力学问题时，为了保证模拟结果真实可靠，能够真实反映围岩的受力情况，依据圣维南原理和隧洞开挖的影响范围，同时充分考虑锦屏Ⅱ级水电站现场围岩地质条件，以及消除模拟计算所产生的边界效应，建立的计算模型横向长100 m，竖向高80 m，纵向宽60 m，数值模型如图6所示，监测点的布置如图7所示。

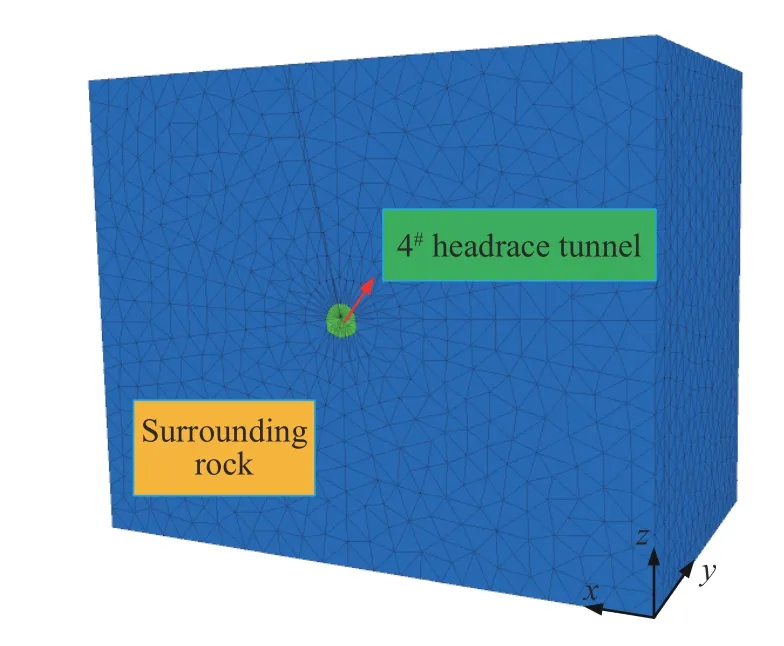
图6 数值模型Fig.6 Numerical model

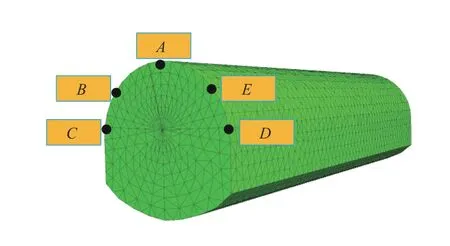
图7 4#引水隧洞监测点位置Fig.7 Monitoring points position of 4# headracetunnel

动力计算时，为使系统的动能快速吸收从而达到收敛，采用Rayleigh 阻尼，最小临界阻尼比取0.05，最小中心频率取500 Hz；该计算模型的上边界为应力约束边界，施加58.09 MPa（现场实测）垂直载荷，计算模型的下边界、前后和左右边界均为位移约束边界条件，模型外围边界设定为静态边界，在模型法向、切向设置阻尼器以减小或消除模拟计算所产生的弹性波反射，为计算模型提供等同于无限场地的约束效果，如图8所示。

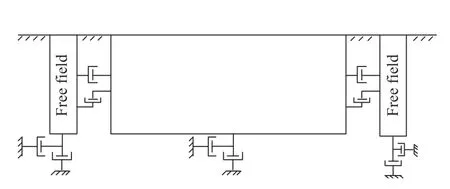
图8 自由场边界示意Fig.8 Free field boundary

3.2 爆破荷载作用形式

岩体爆破是瞬时产生的复杂过程，在洞室中引爆预埋炸药，将瞬间产生不可阻挡的高温高压气体，在洞室内部急剧膨胀，产生的爆炸冲击波作用于洞室内壁，并迅速衰减为应力波，整个过程的持续时间仅数毫秒。由于爆炸机理及影响因素极其复杂，使爆炸过程的细节很难定量确定，在数值分析中爆破荷载常假定为一个三角形冲击波[41–42]，如图9所示。三角形函数爆炸荷载历程曲线表达式如式(18)。通过对三维离散元软件进行二次开发，采用FISH 编写程序语言施加动荷载，并利用APPLY命令施加到隧道开挖轮廓面。

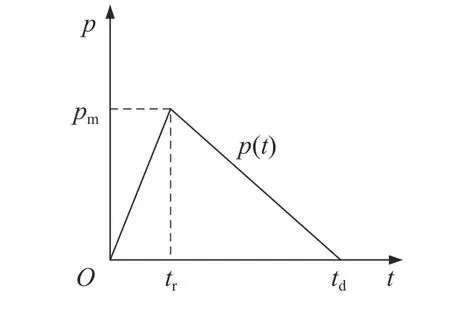
图9 爆破荷载曲线Fig.9 Blasting load curve

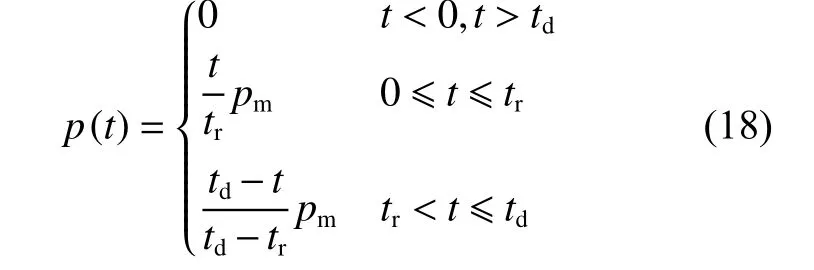
式中：p(t)为 任一时刻的爆破荷载压力值；pm为爆破荷载峰值，pm=60 MPa；tr为爆破荷载上升至峰值的时间，tr= 0.3 ms；td为爆炸荷载的正压作用时间，td= 1 ms。

3.3 本构关系及屈服准则

在数值模拟中，本构模型的选取需要与工程材料力学特性有很高的契合度。为真实反映围岩受力状况，结合2.3节中6个评价指标的定义，模型本构关系采用描述硬岩力学行为的Mohr-Coulomb屈服准则[43]

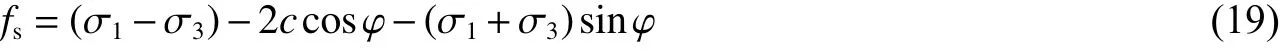
式中：c为黏聚力， φ为摩擦角。

该准则的破坏包络线与剪切屈服函数以及拉应力屈服函数相对应，是一个与拉伸破坏相关的流动法则，当fs＜0时，岩体将会发生剪切破坏。围岩的物理力学参数参照中国科学院武汉岩土力学研究所锦屏项目组地应力及岩体力学参数的反演结果[4]，如表6所示，其中：cm为黏聚力峰值，cr为黏聚力残余值， φ0为摩擦角初始值， φm为摩擦角峰值， ψ为剪胀角。在数值模拟时对岩石岩性作出假设：岩石为均质、各向同性的连续体，符合Mohr-Coulomb强度准则，材料参数满足Mohr-Coulomb本构模型关系。

表6 岩体的物理力学参数Table 6 Physical and mechanical parametersof rock

3.4 隧洞岩爆分析

由图4可知，4#引水隧洞岩爆发生在洞室掌子面后方约80 m 范围内。该隧洞开挖采用上下台阶法，仅对洞室进行上台阶开挖时（开挖高度8.5 m，见图5）就发生了岩爆，因而选取岩爆区域的中间位置（K9+765附近）进行分析。

在数值模拟中，通过对3DEC软件进行二次开发，采用FISH 编程编写计算函数来实现式（2）、式（7）和式（12）的表达，并监测所有计算块体单元的变化过程。本节将依据数值模拟结果并运用预测评价指标对岩爆倾向性进行评价，如图10～图18所示，其中：图10、图11、图14与图16是隧洞在爆破作用1 ms后的分布云图。

（1）能量释放演化过程分析

由图10、图11和图12可知，洞室开挖后，主应力差最小值多集中在洞室右侧拱肩、拱腰及拱底处，而现场实际情况为隧洞掌子面右侧边墙及拱腰部位的混凝土喷层也出现了膨胀开裂，如图13所示。主应力差最大值多集中在洞室左侧拱肩、拱腰及拱脚处，进一步依据岩石力学理论可知，位于主应力差最大值处的岩体储能极限也会显著增加。结合弹性应变能密度分布云图发现，在动力开挖扰动下，靠近洞室临空面的围岩体均出现了不同程度的弹性应变能释放现象，并且随着与隧洞中心距离的增加，弹性应变能释放量逐渐减小，其中洞室两侧拱顶、拱肩、边墙以及拱底处围岩弹性应变能释放量最大，进一步表明洞室周围岩体破裂演化的平缓加速历程也是围岩内部能量不断积聚、耗散的过程，围岩应力高度集中，使得能量积聚增加，当围岩体储存能量超过岩体储能极限时，多余的能量以动能形式迅速释放，导致岩体出现岩爆、片帮、板裂或大变形破坏。

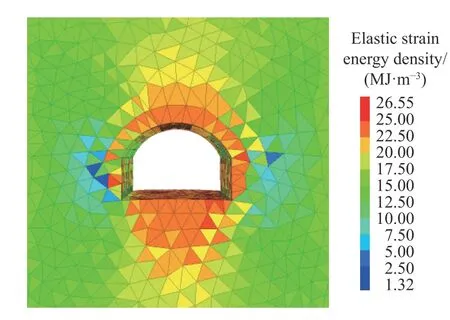
图10 弹性应变能密度分布Fig.10 Distribution of elastic strain energy density

图11 主应力差等值线云图Fig.11 Contour maps of principal stresses difference

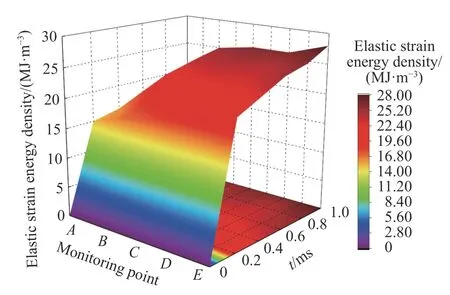
图12 弹性应变能密度时空分布Fig.12 Spatial and temporal distribution of elastic strain energy density

图 13 4#引水隧洞右拱肩喷层鼓胀开裂[44]Fig.13 Bulging cracksat right spandrel of 4# headrace tunnel[44]

图14 岩爆模拟示意图Fig.14 Schematic of rockburst simulation

由图14可知，隧洞左侧岩爆坑位于左拱肩、左拱腰偏下处，爆坑深度为3 m 左右；隧洞右侧岩爆坑位于右拱肩、右拱腰偏上处，爆坑深度为2 m 左右；隧洞最大岩爆坑位于掌子面左侧边墙及拱底处，与现场情况接近，最大岩爆坑深度约为5.4 m；由隧洞破坏形状可知，数值模拟结果与实际岩爆坑的形状（见图15）基本吻合，验证了本研究中建立的岩爆判据预测评价的合理性，同时也能满足对岩爆发生过程进行动态追踪的要求。

图15 现场岩爆坑示意图[21]Fig.15 Schematic of on-site rockburst areas[21]

（2）岩爆能量指标分布特征

由图16可知，洞室断面不同位置处岩爆判据R界限值表现出截然不同的变化规律：在洞室拱顶处，R界限值达到最大值114.54，在距洞室拱顶较远处开始慢慢降低，并一直维持在较低水平；在洞室两侧拱腰以及边墙处，R界限值多集中在25～86之间，可释放部分弹性应变能，有发生中等岩爆的可能；在洞室拱底处，R界限值多集中在90～115之间，有发生强烈岩爆的可能。这也说明围岩在高应力的影响下积聚大量的弹性应变能，当围岩强度超过岩体所承受的极限强度时，围岩发生脆性破坏并瞬间释放大量的弹性应变能，进而发生剥落、弹射甚至抛掷等岩爆现象。

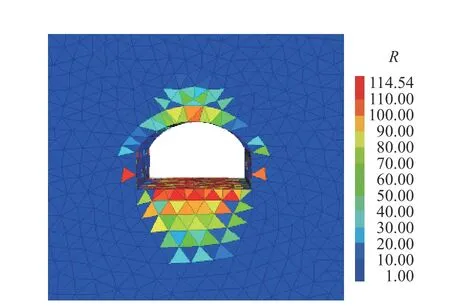
图16 岩爆判别R界限值分布云图Fig.16 Contour maps of rockburst criterion threshold

以洞室右侧拱脚为0°，逆时针旋转一周，得到K9+765标段洞室断面（0°～360°）R界限值，如图17所示。分析图17可知，R界限值的最大值出现在洞室拱顶围岩表面（90°左右）；在角度为0°～90°时，R界限值为5～20，有发生轻微岩爆到中等岩爆的可能；在角度为90°～180°时，R界限值为26～90，有发生中等岩爆的可能；在角度为180°～240°时，R界限值为20～50，也有发生中等岩爆的可能；在角度为240°～360°时，R界限值为80～100，有发生中等岩爆到强烈岩爆的可能。由以上分析可知，数值模拟所得的R界限值与实际工程中发生强烈岩爆的情况较吻合。

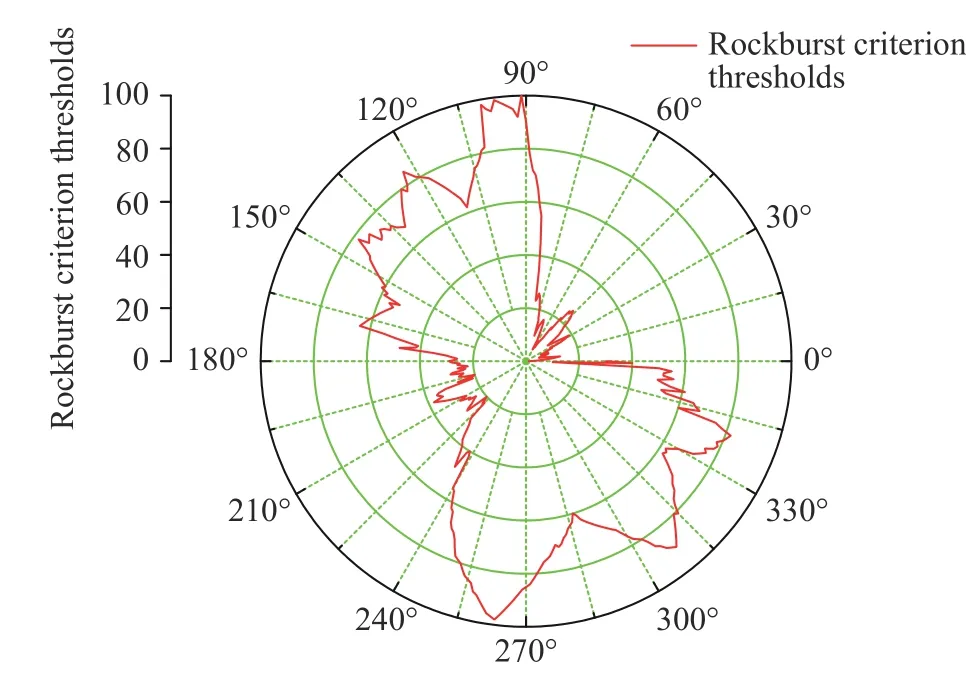
图17 K9+765标段洞室断面（0°～360°）R界限值Fig.17 Rockburst criterion thresholds of K9+765 section

图18为洞室岩爆块体弹射情况，通过分析可知，岩爆破坏主要发生在拱顶、拱肩及拱脚与底板交界处，岩爆倾向性判别指标R基本反映了可能出现岩爆破坏的区域，在R值较大的拱顶、拱肩及拱脚与底板交界位置均出现了岩块的弹射现象，与实际岩爆坑的形状（见图15）较吻合。

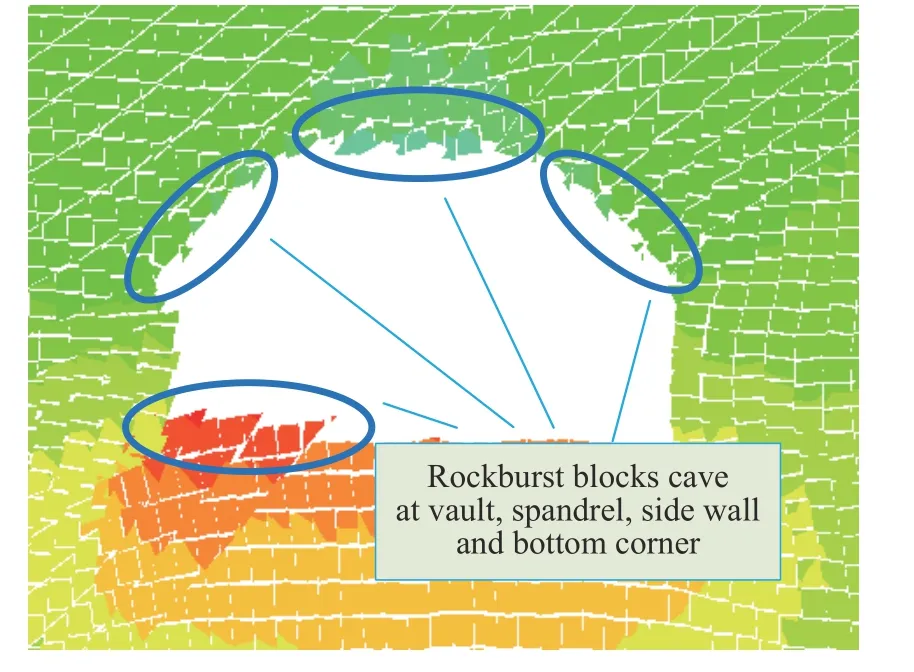
图18 岩爆块体弹射示意图Fig.18 Schematic of rockburst block ejection

综上所述，基于能量原理，建立了一个全面考虑单元体受力的各种状态和4个岩爆主要控制因素的岩爆判据或评价系统。采用数值模拟方法，对相关研究成果进行了系统的综合应用，以锦屏Ⅱ级水电站4#引水隧洞发生的典型岩爆案例为依托，对其进行了数值模拟，所得计算结果与实际情况基本一致，从而验证了所提理论判据及计算方法的合理性。尽管本研究中建立的判据还有待通过其他典型岩爆案例进行进一步验证，以体现该判据的普遍适用性，但该判据为准确预测深部地下工程岩爆倾向性提供了一种新的思路。

4 结 论

以能量原理为基础，以岩爆重要控制因素（力学因素、脆性因素、储能因素与完整性因素）作为岩爆倾向性评估控制因子，全面考虑了单元体受力的各种状态，在已有研究基础上建立了一个新的岩爆倾向性判据，阐述了该判据的构建思想和基本原理，并对部分典型岩爆工程实例进行了验证和数值模拟，得到如下结论。

（1）基于能量原理的岩石动力破坏机制，以岩石强度与整体破坏准则为基准，建立了岩体单元受压与受拉时的岩爆判据与岩爆分级评价系统。

（2）基于能量原理的岩爆倾向性判据意义明确，简单实用，且仅需测定围岩应力、岩石抗拉强度、抗压强度、弹性模量和泊松比，避免了对复杂围岩切向应力和径向应力的计算。

（3）基于能量原理的岩爆倾向性判据全面考虑了围岩单元体受力的各种状态，反映了岩爆孕育发生过程的完整性因素、力学因素、脆性因素与储能因素。其数学表达形式为主应力的乘积，在数值模拟时不需要进行坐标变换，便于运用和操作。

（4）典型岩爆工程实例的计算分析表明，基于能量原理的岩爆倾向性判据对岩爆的预测评估与岩爆发生的实际情况基本一致，具有良好的有效性和工程适用性，可为类似地下工程的岩爆预测提供参考。

感谢贵州大学郭建强教授对本研究工作给予的指导和帮助。