防弹衣抗小钨球侵彻性能的数值模拟

唐昌州，智小琦，郝春杰，范兴华

（1.中北大学机电工程学院，山西 太原 030051；2.晋西工业集团，山西 太原 030027）

防弹衣是士兵生命安全的重要保障。近年来，随着现代武器装备的高速发展，反步兵武器毁伤能力大大增强，士兵面临的生命威胁日益严重，因此对防弹衣的抗侵彻性能提出了更高要求。

迄今为止，针对防弹材料的抗侵彻性能研究，学者们已开展了大量的工作。例如：Flanagan 等[1]研究了凯夫拉（Kevlar）层合板在12 g 圆柱弹侵彻下的失效模式，发现层合板的失效模式与弹丸侵彻速度相关；Sikarwar 等[2]利用7.5 g 圆锥形弹丸侵彻玻璃/环氧复合材料层合板，研究了纤维方向对抗侵彻性能的影响，发现当采用[0°/90°]铺层顺序时，纤维层合板的抗弹性能最好；Naik 等[3]研究了E-玻璃纤维/环氧树脂层合板抗2.8 g 圆柱弹的侵彻性能，结果表明，随着厚度的增加，层合板的抗弹性能大致呈线性增加趋势。Majzoobi等[4]、Jordan 等[5]以及邓云飞等[6]分别研究了3.5、2.85和34.5 g 弹丸的头部形状对纤维层合板抗侵彻性能的影响，发现层合板的抗弹性能与弹丸头部形状相关，弹丸头部越尖，层合板的抗弹性能越差。谢文波等[7]研究了碳纤维层合板在不同侵彻角度下抗1.72 g 钢球的侵彻性能，结果表明，低速时，正侵彻下的靶板能量吸收率高于斜侵彻，层合板抗侵彻性能随侵彻角度的增大而降低，高速时结论则相反。秦建兵等[8]利用数值模拟方法研究了同一厚度、不同层数的纤维层合板抗5.2 g弹丸的侵彻性能，发现当初速远低于或远高于弹道极限时，层合板的抗弹性能几乎不受纤维层数的影响；当初速接近弹道极限时，纤维层数对层合板的抗弹性能影响显著，可以通过适当增加纤维层数的方式来提高层合板的抗弹性能。此外，针对纤维层的层间混杂效应对纤维复合材料抗5.78 g 锥形弹[9]、7.62 mm[10]和12.7 mm[11]穿甲弹侵彻性能的影响问题也作了相应研究。

从上述研究现状不难看出，防弹纤维的抗侵彻研究大多围绕大质量弹丸或标准枪弹展开，而关于抗小质量破片的侵彻研究相对较少。根据美国陆军军医局对第二次世界大战后历次现代战争的战伤数据统计，80%以上的士兵伤亡是由手榴弹、迫击弹和其他爆炸物的破片所致。美军纳蒂克研究所对不同弹种爆炸后形成破片的质量分布统计则表明，不同弹丸爆炸后形成的破片质量以1 g 以下居多[12]。因此针对防弹纤维开展抗小质量破片侵彻研究具有一定的现实意义和实用价值。

由于钨合金球形破片材料密度大、强度高、存速高，可有效提高杀伤威力，而Kevlar 目前广泛应用于防弹产品领域，因此，拟针对小钨球侵彻Kevlar 软质防弹衣开展试验研究，在此基础上，利用数值模拟方法对侵彻过程及小钨球侵彻作用下防弹衣的破坏机理进行研究，并探讨不同防弹材料的层间混杂配比对防弹衣抗小钨球侵彻性能的影响，以期为提高防护装备的防护性能提供参考。

1 试 验

1.1 试验布置

试验所用小钨球的质量为0.16 g，直径为2.8 mm，靶板为FDY3R-01型三级软质防弹衣，防弹层材料为Kevlar，共45层，总厚度为9 mm。试验利用12.7 mm 滑膛弹道枪发射置于尼龙弹托中的小钨球。发射后，在空气阻力作用下，钨球与弹托分离。为防止弹托上靶，在靶板前设置挡板，挡板上有比弹托小的孔。为测量小钨球的着靶速度和剩余速度，在靶前及靶后分别设置梳妆通断靶，测速装置采用南京理工大学机械工程学院设计的NLG202-Z型六路测速仪，精度为0.1µs。图1为试验所用的破片及弹托，图2为试验布置示意图。本次试验中的侵彻均为正侵彻。

图1 破片及弹托Fig.1 Fragments and sabots

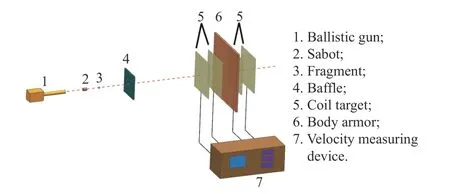
图2 试验布置示意图Fig.2 Schematic diagram of experimental set-up

1.2 试验结果及分析

表1给出了小钨球侵彻防弹衣的试验数据。由表1可知，小钨球侵彻防弹衣的弹道极限在725.3～732.7 m/s之间。由于两者速度差在15 m/s以内，弹道极限可取平均值[13]，故0.16 g 小钨球侵彻三级Kevlar 软质防弹衣的弹道极限为729 m/s。

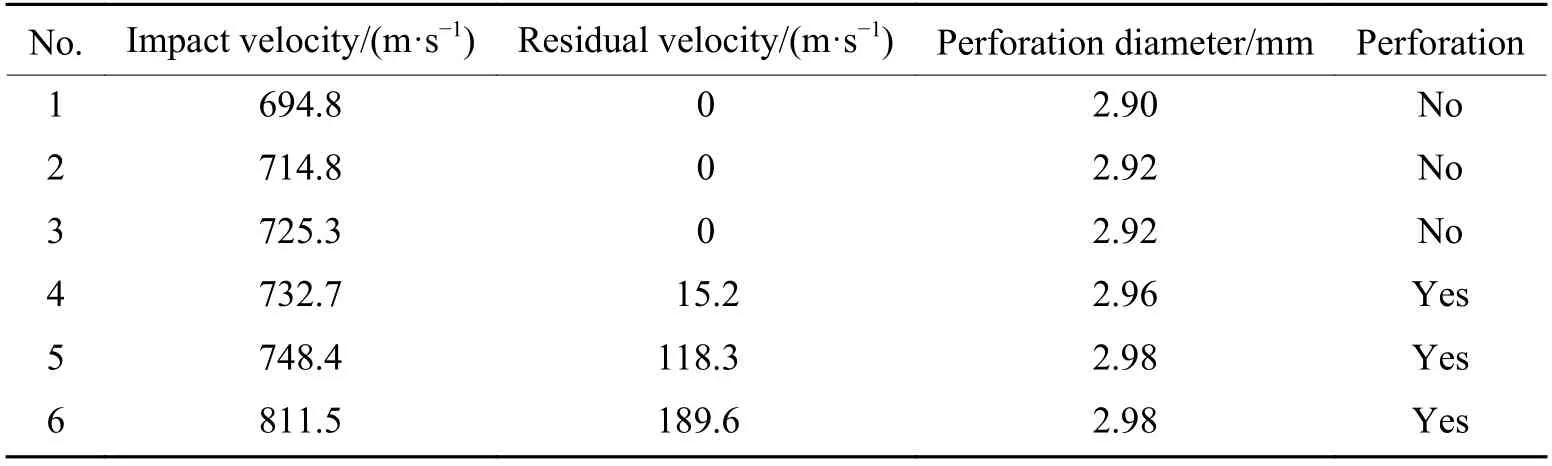
表1 试验数据Table 1 Experimental data

图3给出了防弹纤维的典型破坏状态。由图3(a)可知，在小钨球侵彻作用下，防弹衣的迎弹面纤维发生剪切破坏，并产生一个比钨球稍大的弹孔，弹孔周围存在一定的烧焦痕迹。这是由于在剪切过程中，小钨球受到剧烈摩擦作用，温度急剧上升导致弹孔附近发生一定的烧蚀，因而弹孔直径比钨球直径稍大。而防弹衣的背弹面纤维则在小钨球侵彻作用下发生拉伸断裂破坏。这是由于在侵彻过程中，纤维将小钨球的部分动能吸收并转化为自身的弹性势能，宏观表现为纤维的拉伸变形。当拉伸强度超过纤维的弹性极限时，纤维发生塑性变形，背弹面局部区域发生鼓包现象，如图3(b)、图3(c)所示。随着小钨球的继续深入，当拉伸强度达到纤维的断裂强度时，纤维发生断裂破坏，小钨球逐步完成穿孔，背弹面纤维与树脂发生脱粘现象，如图3(c)所示。

图3 防弹纤维的典型破坏状态Fig.3 Typical failure states of bulletproof fiber

2 数值模拟

为进一步分析防弹衣在小钨球侵彻作用下的损伤破坏机理，并探讨不同防弹材料的层间混杂配比对防弹衣抗侵彻性能的影响，采用数值模拟方法对防弹衣抗小钨球侵彻性能进行研究。

2.1 有限元模型的建立

通过TrueGrid 软件进行建模和网格划分，钨球尺寸和防弹衣厚度与试验参数保持一致。防弹衣选用圆形靶并采用分层建模，每层0.2 mm，共45层，模型均采用8节点6面体单元。为减小边界效应对侵彻结果的影响，靶板直径定为60 mm（大于钨球直径20倍以上）。为保证计算的时长与精度，网格采用渐进式。弹靶相互作用的主要区域进行网格加密，网格尺寸控制在0.10～0.15 mm；其他区域网格向四周逐渐稀疏过渡，网格尺寸控制在0.15～1.27 mm；钨球最小网格尺寸为0.01 mm。为节省计算时间，考虑到模型的对称性，模型截取1/4，如图4所示。

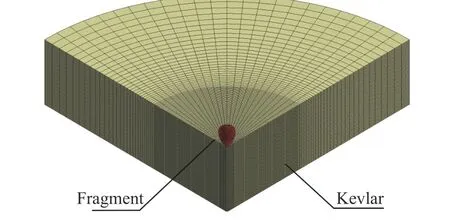
图4 有限元模型Fig.4 Finite element model

利用LS-DYNA 软件进行数值模拟，采用Lagrange 算法，系统单位制设定为cm-g-µs。根据模型结构的对称性，在对称截面采用对称边界条件。为忽略边界反射的影响，在靶板边缘添加非反射边界条件。弹靶之间的接触定义为面面侵蚀接触。防弹衣纤维层与层之间采用固连失效接触，其失效准则为

式中： σn为 法向应力， σs为 切向应力，σNL为层间法向强度， σSL为层间切向强度。参考文献[14]，σNL设为25 MPa， σSL设为20 MPa。

钨球采用双线性弹塑性本构模型PLASTIC_KINEMATIC进行描述，该模型利用Cowper-Symonds模型考虑了材料的应变率效应，表达式为

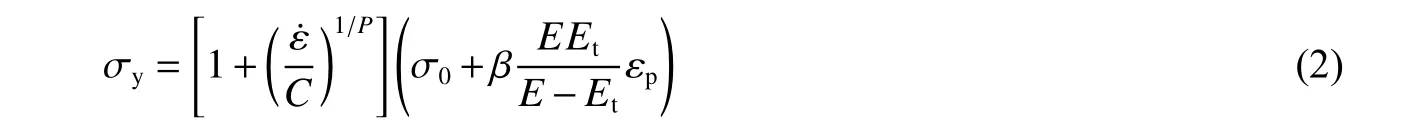
式中： σy为动态屈服强度； ε˙为有效应变率；C、P为应变率参数； σ0为静态屈服强度； β为硬化参数；E为弹性模量；Et为切线模量； εp为有效塑性应变，模型采用最大塑性应变失效准则。本次模拟使用的钨球材料模型参数[15]见表2，其中： ρ为密度， µ为泊松比， εf为失效应变。

表2 钨球材料模型参数Table 2 Material model parameters of tungsten sphere

由于防弹衣属层合结构且具有正交各向异性的特点，故防弹衣采用基于经典层合理论和Chang-Chang失效准则[16–17]的复合材料损伤本构模型COMPOSITE_DAMAGE进行描述。该模型能较好地模拟正交复合材料的失效，其应力-应变关系为

式中： ε和 γ为应变， σ和 τ为应力，G为剪切模量，下标1、2、3表示材料的弹性主方向。

Chang-Chang 失效准则将纤维的失效形式分为以下4种。

（1）纤维的拉伸失效

式中：XT为纵向拉伸强度，SC为面内剪切强度， δ为失效参数。

（2）纤维的压缩失效

式中：XC为纵向压缩强度。

（3）基体的拉伸失效

式中：YT为横向拉伸强度。

（4）基体的压缩失效

式中：YC为横向压缩强度。

参考文献[18]，根据试验结果对材料参数进行微调，Kevlar 的材料模型参数如表3所示。其中：Kf为损坏材料的体积模量，α为非线性剪切应力修正系数，SN为法向拉伸强度，S13和S23为横向剪切强度。

表3 Kevlar 材料模型参数Table 3 Material model parameters of Kevlar

2.2 有限元模型的验证

利用上述有限元模型对各试验工况进行数值模拟，结果如表4所示。由表4可知，数值模拟得到的剩余速度及弹孔尺寸与试验结果相近，且弹道极限的相对误差仅为0.41%，表明该有限元模型及其参数可靠。不过值得注意的是，模拟得到的弹孔尺寸均小于试验值。这是由于在数值模拟中并未考虑温度对烧蚀的影响。

表4 仿真值与试验值的比较Table 4 Comparison between simulation results and experimental results

2.3 侵彻过程及破坏机理分析

图5给出了不同着靶速度下防弹衣的破坏情况。由图5可知，当着靶速度v低于弹道极限时，防弹衣的破坏模式主要表现为迎弹面纤维的剪切破坏和背弹面纤维的拉伸断裂破坏，并伴随着一定程度的层间分层破坏，如图5(a)、图5(b)所示；当着靶速度在弹道极限附近时，纤维的层间分层破坏显著，如图5(c)所示；当着靶速度高于弹道极限时，随着着靶速度的提高，纤维的拉伸和层间分层破坏程度下降，如图5(d)、图5(e)和图5(f)所示。

图5 不同着靶速度下防弹衣的破坏情况Fig.5 Failure modes of body armor at different impact velocities

以工况5为例，详细分析弹靶相互作用机制，图6给出了小钨球侵彻防弹衣过程中的von-Mises应力变化。由图6可知：t= 1µs时，钨球开始侵彻防弹衣，此时由于撞击产生沿防弹衣厚度方向传播的压缩波，弹靶接触区域的纤维层在压缩波作用下发生压缩变形，并获得一定的速度，如图6(a)所示。与此同时，由于弹靶接触区域与非接触区域的纤维存在较大的速度梯度，纤维层面内产生面内剪切波，当剪切波强度超过应力极限时，纤维发生剪切破坏，如图6(b)所示。t=5µs时，压缩波传递至纤维层背面，由于背面无约束，纤维层背面产生微小拉伸变形，如图6(c)所示，并且压缩波会在纤维层背面反射形成拉伸波，拉伸波沿侵彻方向相反的方向传播。随着侵彻的进行，未被侵彻的纤维层拉伸变形加剧，纤维层的破坏模式逐渐由剪切破坏向拉伸变形破坏转变，在此过程中，当拉伸波强度超过纤维层间结合强度时，部分纤维发生分层破坏，如图6(d)所示。t=20µs时，弹靶接触区域的纤维层速度与钨球速度基本相同，未被侵彻的纤维层在钨球推动作用下形成动态变形锥，如图6(e)所示。随着钨球的深入，变形锥锥角逐渐变大。t=26µs时，变形锥运动到极限位置，此时的纤维处于极限拉伸状态，如图6(f)所示。当钨球进一步侵彻时，纤维开始逐层发生拉伸断裂破坏，并且纤维的层间分层破坏也不断加重，如图6(g)所示。t= 64µs 时，钨球贯穿纤维层，侵彻过程结束，如图6(h)所示。

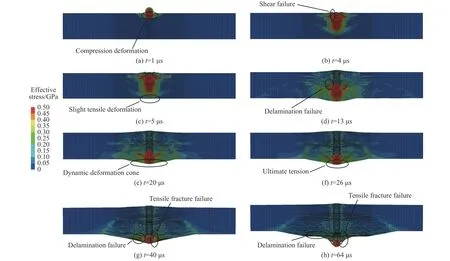
图6 小钨球侵彻防弹衣过程中的von-Mises 应力变化（v =748.4 m/s）Fig.6 Von-Mises stressvariation of small tungsten sphere penetrating into body armor (v = 748.4 m/s)

图7给出了纤维层面内的von-Mises应力变化。由图7可知，纤维轴向上的波阵面形状类似双扭线，层面内的剪切波在弹着点以“十”字形向四周扩散。

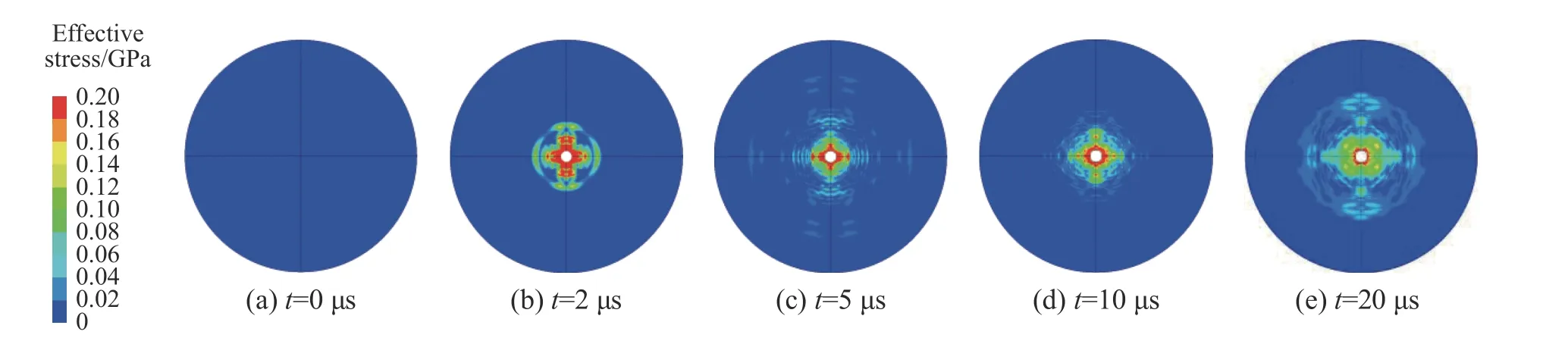
图7 纤维层面内的von-Mises应力变化（v = 748.4 m/s）Fig.7 Von-Misesstress variation on fiber layer (v = 748.4 m/s)

2.4 纤维混杂配比对防弹衣抗侵彻性能的影响

由2.3节中对破坏机理的分析可知，在小钨球侵彻作用下，防弹衣的迎弹面发生纤维剪切破坏，背弹面发生纤维的拉伸断裂和层间分层破坏。因此，为了提高防弹衣的抗侵彻性能，可以从提高迎弹面纤维材料的抗剪强度和背弹面纤维材料的抗拉强度两方面考虑。目前，软质防弹衣大多采用Kevlar 或超高分子量聚乙烯（Ultra-high molecular weight polyethylene,UHMWPE）作为单一防弹材料，虽然后者的防弹性能相对较好，但价格相对昂贵，不如前者应用广泛。由文献[19]可知，与Kevlar 相比，UHMWPE的密度较小，比强度和比模量较大，具有较高的延伸率和冲击韧性，但抗剪切性能和耐高温性能较差。因此，防弹衣迎弹面采用Kevlar、背弹面采用UHMWPE的设计既能提高抗侵彻性能，又能减轻防弹衣的重量。为研究在同一厚度下Kevlar 和UHMWPE的混杂效应对防弹衣抗侵彻性能的影响，本研究对面板为Kevlar、背板为UHMWPE 的不同配比（厚度方向上不同纤维体积分数的比值）的防弹衣抗小钨球侵彻性能进行数值模拟。

数值模拟中UHMWPE仍选用COMPOSITE_DAMAGE 本构模型进行描述，其具体材料模型参数[18]如表5所示。

表5 UHMWPE材料模型参数[18]Table5 Material model parameters of UHMWPE[18]

2.4.1混杂配比对弹道极限的影响

对小钨球侵彻结构分别为K1U1、K1U2和K1U4的防弹衣进行数值模拟，结果如表6所示，其中：K 1U1表示面板Kevlar 与背板UHMWPE的体积配比为1∶1，K 1U2表示面板Kevlar 与背板UHMWPE 的体积配比为1∶2，K1U4表示面板Kevlar 与背板UHMWPE的体积配比为1∶4。

表6 小钨球侵彻不同结构防弹衣弹道极限的仿真结果Table 6 Simulation results of ballistic limit of small tungsten sphere penetrating into body armor with different structures

图8给出了小钨球侵彻不同结构防弹衣时的弹道极限。由图8可知，与侵彻由单一Kevlar 制作的防弹衣（用K1U0表示）相比，小钨球侵彻Kevlar/UHMWPE混杂结构的防弹衣所需的弹道极限更大。当Kevlar/UHMWPE 的体积配比分别为1∶1、1∶2和1∶4时，防弹衣的抗侵彻性能分别提升3.7%、5.3%和4.4%，质量分别减少14.1%、18.8%和22.5%。从提高抗侵彻性能和减轻重量两方面考虑，防弹衣采用Kevlar/UHMWPE纤维体积配比为1∶2的混杂结构时，抗侵彻性能最佳。

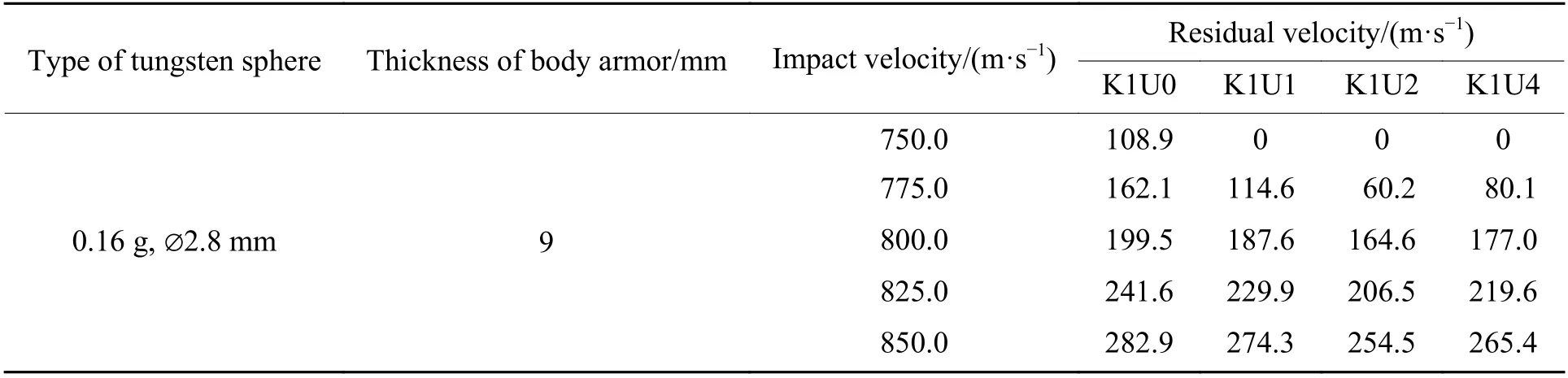
表 7 小钨球侵彻不同结构防弹衣的仿真结果Table 7 Simulation results of small tungsten sphere penetrating into body armor with different structures

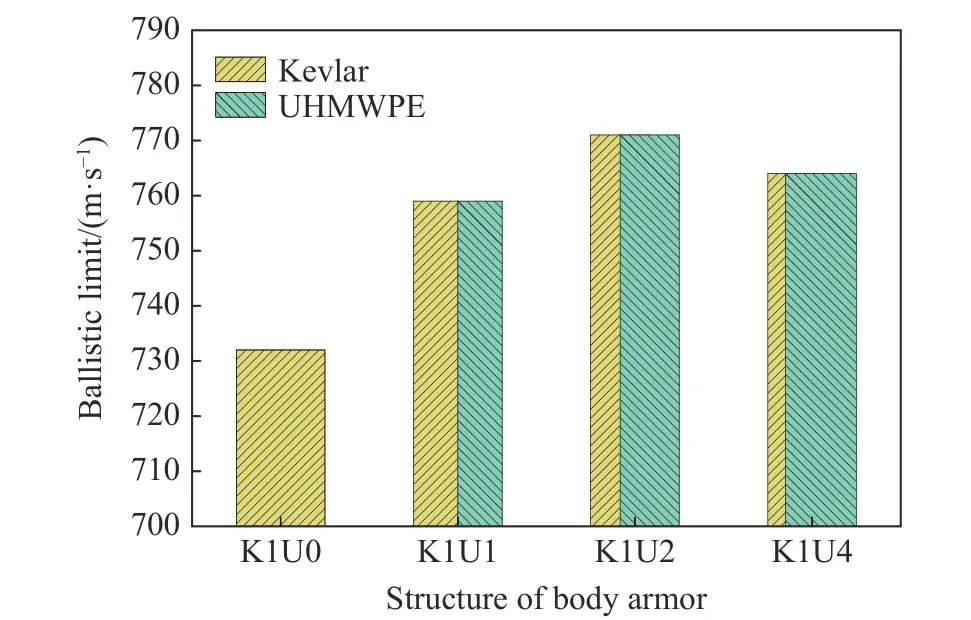
图8 小钨球侵彻不同结构防弹衣的弹道极限Fig.8 Ballistic limit of small tungsten sphere penetrating into body armor with different structures

2.4.2混杂配比对剩余速度的影响

从图9(b)中可以看出，小钨球侵彻K1U0结构防弹衣的负加速峰值最大，即阻力峰值最大。这是由于在0＜t＜7µs阶段，纤维层主要以剪切破坏为主，纤维层的剪切强度对小钨球侵彻阻力影响较大。由于K1U0、K1U1、K1U2、K1U4结构中Kevlar 的体积分数依次减小，因此对应的防弹衣迎弹面的抗剪性能依次减弱，因而在该阶段小钨球侵彻上述4种结构防弹衣的负加速度依次减小，即阻力依次减小。t＞7µs时，纤维层主要发生纤维断裂和分层破坏，小钨球的侵彻阻力受纤维拉伸强度影响较大。由于该阶段纤维层的损伤破坏模式较复杂，且纤维层逐层破坏明显，因而小钨球的加速度曲线波动较大。但从总体来看，K1U0、K1U1、K1U2和K1U4结构中的UHMWPE数量依次增加，K1U0、K1U1、K1U2和K1U4结构防弹衣的背弹面的抗拉性能依次增强，在该阶段小钨球侵彻上述4种结构防弹衣的负加速度大致呈递增趋势，即阻力依次增大。

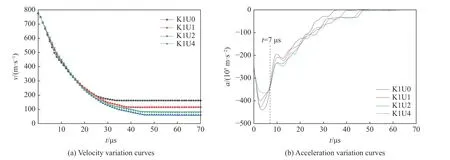
图9 小钨球侵彻不同结构防弹衣的速度和加速度变化曲线（v = 775.0 m/s）Fig.9 Velocity and acceleration variation curves of small tungsten sphere penetrating into body armor with different structures (v = 775.0 m/s)

图10给出了t=7µs时，小钨球侵彻不同结构防弹衣的仿真结果。由图10可以看出，t=7µs时，对于K1U1结构的防弹衣，小钨球还未开始侵彻UHMWPE；对于K1U4结构的防弹衣，小钨球已经开始侵彻UHMWPE；而对于K1U2结构的防弹衣，小钨球刚开始侵彻UHMWPE。t=7µs时，K1U2结构中Kevlar 的抗剪性能得到充分发挥，此后UHMWPE的抗拉性能也能得到充分发挥。因此在K 1U1、K1U2和K1U4结构中，K1U2结构的防弹衣能够最有效地发挥Kevlar 和UHMWPE的协同作用，使得防弹衣的能量吸收最高，体现在钨球剩余速度最小。

图10 小钨球侵彻不同结构防弹衣的仿真结果（v =775.0 m/s,t = 7µs）Fig.10 Simulation results of small tungsten sphere penetrating into body armor with different structures(v = 775.0 m/s,t = 7µs)

图11对比了小钨球侵彻不同结构防弹衣的剩余速度。由图11可以看出，在弹道极限附近时，Kevlar/UHMWPE混杂结构比单一Kevlar 结构的防弹衣的剩余速度要低，吸能效果较好。但随着着靶速度的提高，两种结构剩余速度的差异逐渐减小，这主要与靶板的失效模式有关。当着靶速度逐渐提高时，背部纤维的失效模式会逐渐从拉伸失效向剪切失效转变。由此可以推测，在破片高速侵彻时，纤维混杂结构与单一纤维结构的防弹衣在抗侵彻方面并无太大差异。

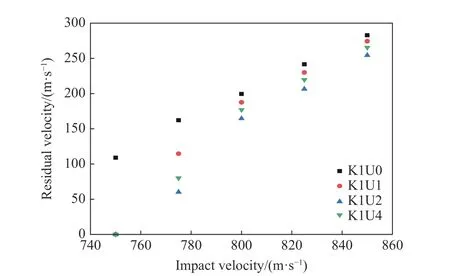
图11 小钨球侵彻不同结构防弹衣的剩余速度Fig.11 Residual velocity of small tungsten sphere penetrating into body armor with different structures

3 结 论

结合试验，利用数值模拟对0.16 g 小钨球侵彻三级Kevlar 软质防弹衣的侵彻过程及破坏机理进行了研究，并探讨了Kevlar/UHMWPE混杂配比对防弹衣抗小钨球侵彻性能的影响，得到以下结论。

（1）在小钨球侵彻作用下，防弹衣迎弹面主要发生纤维的剪切破坏，而背弹面主要发生纤维的拉伸断裂破坏，并伴随着一定的纤维层间分层破坏。而且随着着靶速度的提高，纤维的拉伸及分层破坏程度下降。

（2）与单一Kevlar 制作的防弹衣相比，采用面板Kevlar、背板UHMWPE混杂结构的防弹衣抗侵彻性能更好。当Kevlar/UHMWPE 的体积配比分别为1∶1、1∶2和1∶4时，防弹衣的抗侵彻性能分别提高3.7%、5.3%和4.4%，质量分别减少14.1%、18.8%和22.5%。从提高抗侵彻性能和减轻重量两方面考虑，防弹衣采用纤维配比为1∶2的Kevlar/UHMWPE 混杂结构最佳。

（3）在弹道极限附近时，采用Kevlar/UHMWPE混杂结构防弹衣的吸能效果优于单一Kevlar 结构。而随着着靶速度的提高，两者的吸能差异逐渐减小。