长白山北坡云冷杉阔叶混交林的物种多度格局*

郭跃东 张会儒 卢 军 王卓晖

(1.中国林业科学研究院资源信息研究所 北京 100091； 2.山西农业大学 太谷 030801； 3.国家林业和草原局森林经营与生长 模拟重点实验室 北京 100091； 4.吉林省汪清林业局 汪清 133200)

群落格局与动态过程的关系是群落构建研究的关键内容(Vellend， 2010； Roughgarden， 2009)，森林植物群落的空间格局往往是过去生态过程作用的结果，由格局反演过程已成为当前群落生态学研究的主要手段(McGilletal.， 2007； Matthewsetal., 2014)。但群落装配的生态学格局和过程并不是一一对应的，相同的格局可能由不同的生态过程导致(Huetal., 2006； Stanleyetal.， 2006), 且这些过程也并非是相互排斥的(周淑荣等， 2006； 牛克昌等， 2009)。物种多度格局是群落装配理论的重要结构指标(McGilletal.， 2007)，通过物种多度关系模型的比较，可以指示群落的演替状态(施建敏等， 2015)、检测生态系统的干扰与破坏(Hilletal.， 2002)、解释物种的资源分配和种间关联(Chase， 2005； Sugiharaetal.， 2003)、阐明物种分布的环境筛选机制(石培礼等， 2000； 韩大勇等， 2014; 张姗等， 2015)以及充实生态位模型、群落中性模型及其连续体理论体系(Hubbell， 2006)，为生物多样性和稳定性评价(张立敏等， 2010)及能流、进化、生产力等功能特性关系(Legovic， 1991)研究提供思路。物种多度关系模型主要包括经验统计模型、生态位模型和群落中性理论模型(Pootetal.， 2003； 马克平等， 1997)，其中Hubbell(2001)提出的中性理论模型引发广泛争议(Chisholmetal.， 2010； 周淑荣等， 2006； Volkovetal.， 2003)，争议的焦点是对经验数据格局的模拟哪种模型最佳(Alonsoetal.， 2006； McGilletal.， 2006)，且在争议中不断繁衍出新的模型(McGilletal.， 2007)，朝着联合理论的方向发展(王绪高等， 2008)。目前，国内群落多度格局的报道较多，森林生态系统因其复杂性成为群落多度格局研究的重要方面(冯云等， 2007)，且有关长白山典型森林的群落多度格局研究也较多(王绪高等， 2008； 张姗等， 2015； 闫琰等， 2012)，但大多数研究仍是经验统计模型、生态位模型和群落中性理论模型的对比分析，复合模型以及过伐林群落多度格局的研究尚未见报道。

鉴于此，本研究以长白山北坡云冷杉阔叶混交过伐林为研究对象，通过经验统计模型、生态位模型和群落中性理论模型的对比分析，构建过伐林乔木层物种多度格局生态位复合模型，阐明过伐林群落冠层结构维持的生态过程，探讨生境异质性、密度依赖、种间关联、扩散限制、更新限制和物种分化在针阔混交林群落装配中的作用，以期为揭示过伐林恢复过程中的物种多度分布机制提供理论指导。

1 研究区概况

研究区位于吉林省汪清林业局金沟岭林场，属长白山系老爷岭山脉雪岭支脉，地理坐标为130°05′—130°20′E，43°17′—43°25′N。林区地貌属低山丘陵，海拔 300～1 200 m，坡度主要集中在5°～25°，个别陡坡在35°以上。研究区属季风性气候，1月最低平均气温-32 ℃，7月最高平均气温32 ℃，全年平均气温4 ℃； 年降水量 600～700 mm，多集中在7月。土壤多为灰棕壤土。主要树种有鱼鳞云杉(Piceajezoensisvar.microsperma)、红皮云杉(P.koraiensis)、臭冷杉(Abiesnephrolepis)、沙松(A.holophylla)、黄花落叶松(Larixolgensis)、红松(Pinuskoraiensis)、枫桦(Betulacostata)、白桦(B.platyphylla)、紫椴(Tiliaamurensis)、白榆 (Ulmuspumila)、裂叶榆(U.laciniata)、大青杨(Populusussuriensis)、水曲柳 (Fraxinusmandshurica)、东北红豆杉(Taxuscuspidata)、色木槭(Acermono)、青楷槭(A.tegmentosum)、花楷槭(A.ukurunduense)、朝鲜槐(Maackiaamurensis)等。

2 研究方法

2.1 样地设置与调查

2013年，在研究区设置 12 块面积为1 hm2(100 m×100 m)的固定样地，检尺所有胸径 1 cm 以上林木的特征值，包括树种、胸径、树高、枝下高和冠幅等。按相邻格子法将样地划分成 100 个 10 m×10 m 的小样方，用皮尺定位每株林木的横纵坐标，并于2016和2018年进行复测调查。本研究采用2013年样地初始调查数据，根据主林层优势树种(组)林木生长情况及对应树种的生长过程得知，研究区样地内林分处于中龄林到近熟林阶段，样地基本概况见表 1。研究区林分在中华人民共和国成立前后经过多次采伐干扰，森林蓄积量明显下降， 1998年禁伐后进入次生林恢复经营阶段，此后未采取任何经营措施， 2016年开展目标树抚育间伐，抚育强度为5%～20%。

表1 样地基本概况①Tab.1 Basic characteristics of the twelve sample plots

2.2 物种多度模型拟合与检验

对12块样地乔木层树种多度数据分别构建对数级数模型、对数正态模型、泊松对数正态模型等经验统计模型，几何级数模型、断棍模型、Zipf模型、Zipf-Mandelbrot模型、生态位重叠模型、优势优先模型、随机分配模型等生态位模型，集合群落零和多项式模型和Volkov模型等群落中性理论模型以及复合模型, 拟合物种多度格局。

2.2.1 经验统计模型拟合 采用对数级数模型(logarithm series distribution，ls)(马克平等， 1997)、对数正态模型(logarithm normal distribution，ln)(石培礼等， 2000)和泊松对数正态模型(Poission logarithm normal distribution， pl)对12块样地物种多度分布进行拟合，泊松对数正态模型认为集合(或样本)中1个种包含r个个体的概率为：

(1)

式中： 假设lnλ遵从均值和方差分别为M和V的正态分布；r=1，2，…；λ为泊松分布均值，即物种出现的平均多度(Bulmer， 1974)。

2.2.2 生态位模型拟合 采用几何级数模型(geometrical series model，GS)、断棍模型(random broken sticks model， RBS)、Zipf模型(Zipf)、Zipf-Mandelbrot模型(Mand)、生态位重叠模型(overlapping niche model，ONM)、优势优先模型(dominance preemption model， DPM)和随机分配模型(random assortment model， RAM)对12块样地物种多度分布进行拟合，具体公式见参考文献(马克平等， 1997； 任萍等， 2009； 赵天启等， 2017)。

2.2.3 中性理论模型拟合 1) 集合群落零和多项式模型(metacommunity zero sum polynomial model，MZSM) 该模型假定某一样点的物种多度分布来自于中性复合群落的随机漂变(Alonsoetal.， 2010)，复合群落中任一取样点内多度为n的物种数S可表示为：

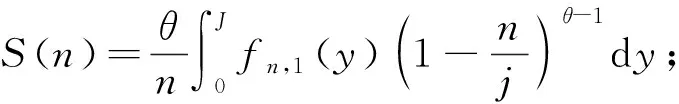
(2)

式中：J为取样点内的个体数；θ为基本生物多样性指数。对数级数模型是该模型的一个特例(Hubbell， 2001)，二者拟合效果非常相似。

2) Volkov模型 该模型在拟合群落物种多度分布时，相较于MZSM模型增加了迁移系数(immigration rate,m)(Volkovetal.， 2003)，并假定此迁移系数在物种从复合群落到局域群落的过程中是不变的(张姗等， 2015)。根据该模型，局域群落内多度为n的物种数S可表示为:

(3)

式中：γ为迁移到局域群落的个体数(Volkovetal.， 2003； 张姗等， 2015);m为迁移系数。

2.2.4 复合模型拟合 群落是指特定生境中共同生活的许多生物种群的集合，复合模型源于1个群落存在2种或多种构建规律，可能最合理的情形是，优势度最前面几个丰富种(常见种)符合生态位模型，后面几个稀有种符合随机分配模型，需要组合生态位分割或重叠和随机生态位分配等模型。Tokeshi(1990)在进行摇蚊(Polypedilum)群落的多度分析时就采用了复合模型。

2.2.5 断面积广义多度模型拟合 由于多度格局仅代表物种多寡的分布，而与森林测定密切相关的胸高断面积更能反映出物种生态位或资源占据状况(Picardetal.， 2002)，因此本研究以胸高断面积作为广义多度指标进行物种广义多度格局分析。目前，物种多度格局研究主要限于以物种个体数作为物种多度指标而忽略了物种个体特征(刘梦雪等， 2010)，如生物量、高度、盖度等，已有研究证明生物量作为物种多度指标的分布不同于以群落物种个体数为指标的分布(Morlonetal.， 2009)。本研究通过上述几种多度模型拟合对比断面积广义多度与传统多度指标的差异。

2.2.6 物种多度模型检验 1) 统计检验 McGill(2003)认为，采用1种模型拟合度检验不能很好判定模型拟合效果好坏，并提出了几种在统计上证明曲线拟合优于零假设的检验方法。本研究采用 Kolmogorov-Smirnov(K-S)检验统计量(D)和卡方检验统计量(χ2)进行物种多度模型检验。

2) 赤池信息准则 赤池信息准则(Akaike information criterion，AIC)是在假设模型误差服从独立正态分布的情况下，为避免过拟合，在模型对数据拟合的优良性与模型的复杂性之间进行权衡，选择AIC最小的模型为最优模型的一种信息标准(Kennethetal.， 2002)。公式如下：

(4)

式中：L为估计模型的似然函数最大值； RSS为剩余平方和；n为样本数；p为参数个数。AIC兼顾模型的简约性和预测的最优性，可避免模型参数冗余。

3) 包络线检验 群落中性理论模型采用随机生成的多次模拟数据进行包络线检验。具体步骤如下： 首先，运用R语言sads包获得群落中性理论模型的基本参数； 然后，运用untb包进行600次多度随机模拟预测分布，计算各排序物种的多度期望值和95%置信区间，取第 2.5%(第 15个)和第 97.5%(585个)作为 95%置信区间的上下限； 最后，通过对比实际观察多度与模拟多度包络线的关系，分析群落中性理论模型的拟合状况(Walkeretal.， 2007)。

2.2.7 数据处理 本研究所有统计分析与模型拟合、检验均采用R-3.4.1中的sads和untb包完成。Shannon-Wiener多样性指数、Marglef丰富度指数、Simpson优势度指数和Pielou均匀度指数计算采用vegan包完成，计算公式见参考文献(马克平等， 1997)。

3 结果与分析

3.1 经验统计模型拟合

采用对数级数模型(ls)、对数正态模型(ln)和泊松对数正态模型(pl)对12块云冷杉阔叶混交过伐林样地乔木层物种多度分布进行拟合，其拟合检验统计量见表2。

表2 物种多度格局拟合的经验统计模型检验统计量①Tab.2 Empirical statistical model test of species abundance pattern

由表2可知，从拟合检验统计量χ2通过比例看，对数级数模型好于对数正态模型和泊松对数正态模型，而从D和AIC指标看，对数正态模型和泊松对数正态模型好于对数级数模型。样地1、3、4未通过χ2显著性检验，样地2未通过K-S检验，表明这些群落采用经验统计模型拟合效果不佳。图1中样地7和1物种多度分布的经验统计模型拟合对比也得到相似结论，样地7拟合效果较好，样地1较样地7拟合效果差一些。表2还表明，D和AIC统计量在群落多度格局拟合检验中表现一致，而χ2检验相对较差。

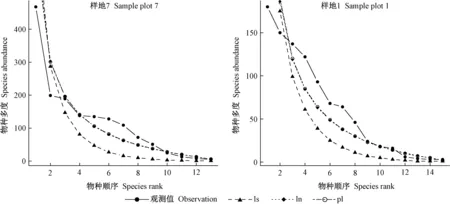
图1 物种多度格局的经验统计模型拟合Fig. 1 Fitting curve of empirical statistical model of species abundance pattern

3.2 群落多样性参数

对数级数模型参数T和对数正态模型参数λ可作为表征群落多样性的重要参数，以个体数和胸高断面积为指标的Shannon-Wiener多样性指数、Marglef丰富度指数、Simpson优势度指数和Pielou均匀度指数计算结果见表3，经验统计模型参数与群落多样性参数之间的相关性分析见表4。

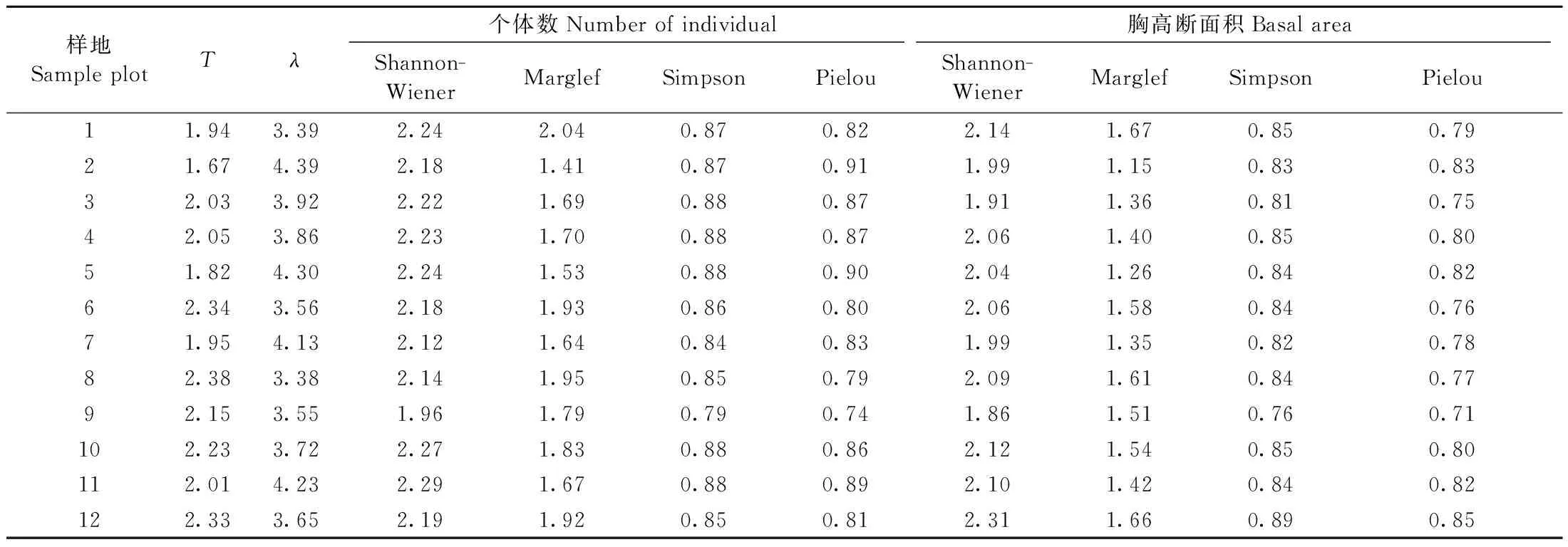
表3 物种多度分布拟合的经验统计模型多样性参数与群落α多样性参数Tab.3 Biodiversity parameters of fitting species abundance model and alpha biodiversity parameters

表4 物种多度分布拟合的经验统计模型多样性参数与群落多样性参数相关性分析①Tab.4 Correlation analysis between biodiversity parameters and fitting parameters from empirical statistical models

由表3可知，除样地12外，以胸高断面积为指标的群落多样性参数明显高于以个体数为指标的群落多样性参数，表明群落中稀有种胸径较大，且大多为优势林冠层的重要伴生种，也可能是过伐林残留林冠层的组分。由表4可知，参数T与λ呈显著负相关，参数T与Marglef丰富度指数呈显著正相关、与Pielou均匀度指数呈显著负相关、与Shannon-Wiener多样性指数和Simpson优势度指数无显著相关性。参数λ与群落多样性参数的关系类似于参数T，但符号相反。Shannon-Wiener多样性指数与Simpson优势度指数、Pielou均匀度指数呈显著正相关，Marglef丰富度指数与多度的Pielou均匀度指数呈显著负相关、与断面积的Pielou均匀度指数不相关，Simpson优势度指数与Pielou均匀度指数呈显著正相关。

3.3 生态位模型拟合

采用几何级数模型(GS)、断棍模型(RBS)、Zipf模型(Zipf)、Zipf-Mandelbrot模型(Mand)、生态位重叠模型(ONM)、优势优先模型(DPM)和随机分配模型(RAM)对12块云冷杉阔叶混交过伐林样地乔木层物种多度分布进行拟合，其拟合检验统计量见表5。各模型对群落物种多度分布的拟合及实际观测数据见图2。

表5 物种多度格局的生态位模型检验统计量Tab.5 Niche model test of species abundance pattern

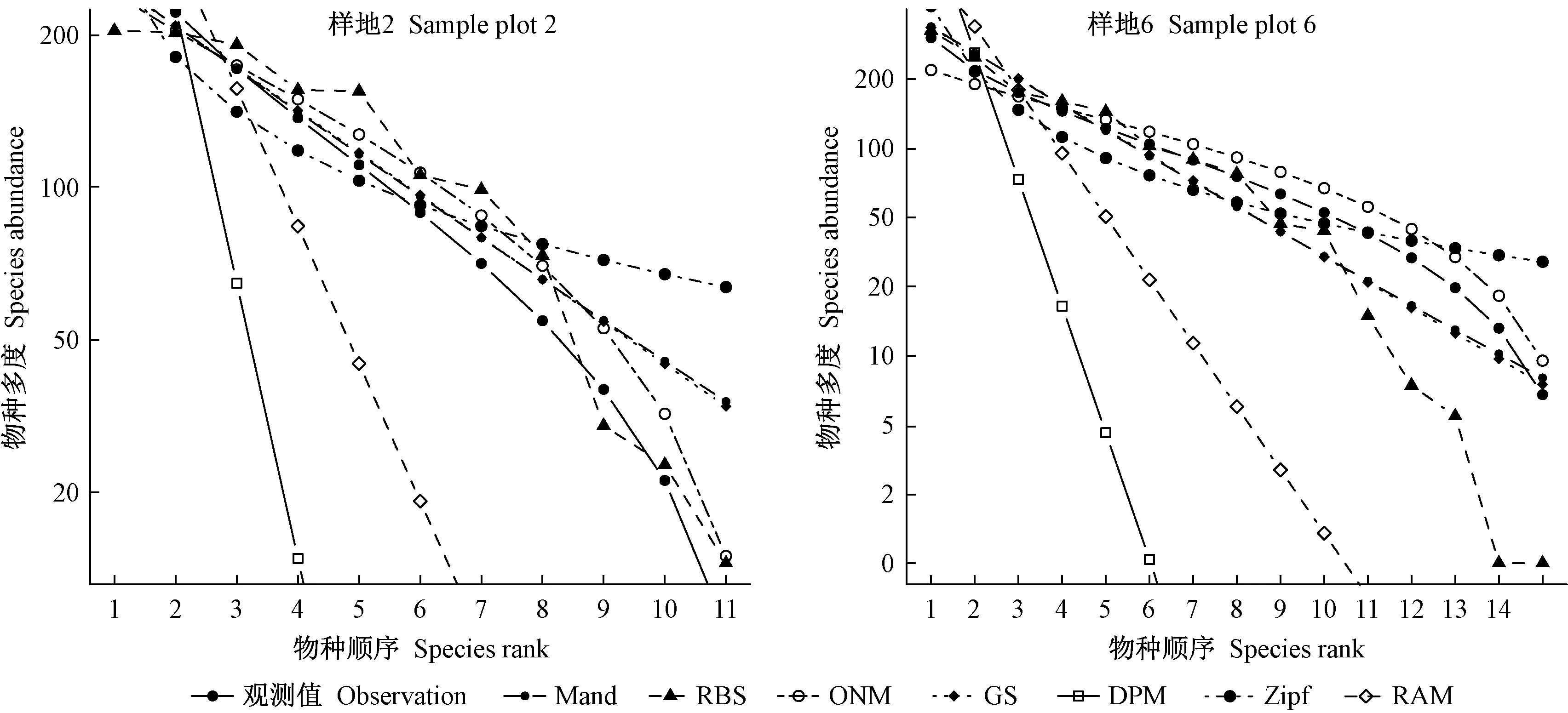
图2 物种多度格局的生态位模型拟合Fig. 2 Fitting curve of niche model of species abundance pattern

由表5可知，不同生态位模型对群落物种多度分布的拟合存在较大差异，按照拟合优良性表现指标，断棍模型拟合效果最佳，其次是生态位重叠模型和几何级数模型，再次为Zipf模型和Zipf-Mandelbrot模型，最后为随机分配模型和优势优先模型(图2)。采用断棍模型、生态位重叠模型和几何级数模型，所有群落优势度多度曲线均具有一个明显的拟合陡变点，在重要性排序轴的前半段，表征群落多度均匀性的曲线陡度较缓，3种模型的拟合效果均较好，尤其是生态位重叠模型，而在重要性排序轴的后半段，曲线急剧下降，3种模型的拟合效果均较差(图2)，表明群落是由5～8个明显的优势种(丰富种)组成的群落，群落物种多度格局可能存在2种规律，丰富种和稀有种多度呈2个明显的竞争等级，采用复合模型可能具有更高的拟合优良性。

3.4 中性理论模型拟合

采用零和多项式模型(MZSM)和Volkov模型(Volkov)对12块云冷杉阔叶混交过伐林样地乔木层物种多度分布进行拟合，其拟合检验统计量见表6。群落物种多度分析的Volkov模型包络线检验见图3。

表6 物种多度格局的中性理论模型检验统计量①Tab.6 Neutral theory model test of species abundance pattern

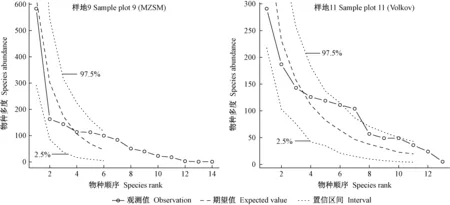
图3 物种多度格局的中性理论模型包络线检验Fig. 3 Envelop test of synthetic data from different neutral theory model

由表6 可知，所有样地零和多项式模型的χ2统计量均大于15，除样地4、9、11外，其他样地的零和多项式模型均未通过显著性检验，而所有样地的Volkov模型均通过统计检验，表明Volkov模型可用于拟合群落的物种多度格局，但其χ2明显高于生态位模型，即Volkov模型拟合并不是最佳的。图3群落中性理论模型包络线检验结果也表明Volkov模型优于MZSM模型。样地9和11的大多数物种多度观测值明显偏离中性理论期望值，重要性排序居中的物种多度甚至达到或超出600次随机模拟的97.5%包络线(群落11表现尤甚)，少数物种的多度也达到或超出2.5%置信区间(图3)，且少数稀有种或伴生种的多度预测为0，无法体现群落生物多样性状况，尤其是MZSM模型。这表明群落中性理论模型用于物种优势度多样性曲线拟合相对较差，换言之，群落中各物种的多度分布并不是独立、随机的，而是受某种特定的生态位过程机制制约。

3.5 复合模型拟合

由上述分析可知，经验统计模型中对数正态模型和泊松对数正态模型较对数级数模型拟合效果好，可能与群落中中间倍程的物种数较多、优势种或稀有种的物种数较少有关(图1)。生态位模型拟合效果较经验统计模型好，可能是因为群落中存在明确的生态位过程，制约群落资源分配，影响物种多度，但观测值具有明显的拐点特征，表明群落物种多度格局存在2种或2种以上规律。本研究采取以下步骤进行复合模型拟合： 首先，从物种多度观测曲线上(图2)找出陡度明显变化陡变点的物种序号，将多度数据分为前后2个数据集进行分段拟合，所有群落陡变点前物种数据趋向于各物种多度分配均衡状态，采用断棍模型和生态位重叠模型可能更能反映该情况，而陡变点后物种数据趋向于多度分配明显失衡状态，采用随机分配模型、优势优先模型和断棍模型可能更能反映该情况； 其次，对2个数据集分别采用前述参试模型组成6种复合模型进行群落物种分布拟合，得到最佳复合模型拟合方法。在分段拟合时，涉及最优陡变点的问题，观察记录明显陡变点的物种序号，前后推移各3个序号，采用Lai等(2013)的最大似然法确定最佳临界值。本研究利用AIC最小值获得复合模型拟合陡变点最佳序号，以方便比较各复合模型的表现。表7所示为物种多度分布数据的复合模型拟合结果，图4所示为群落物种序列-多度格局实例。

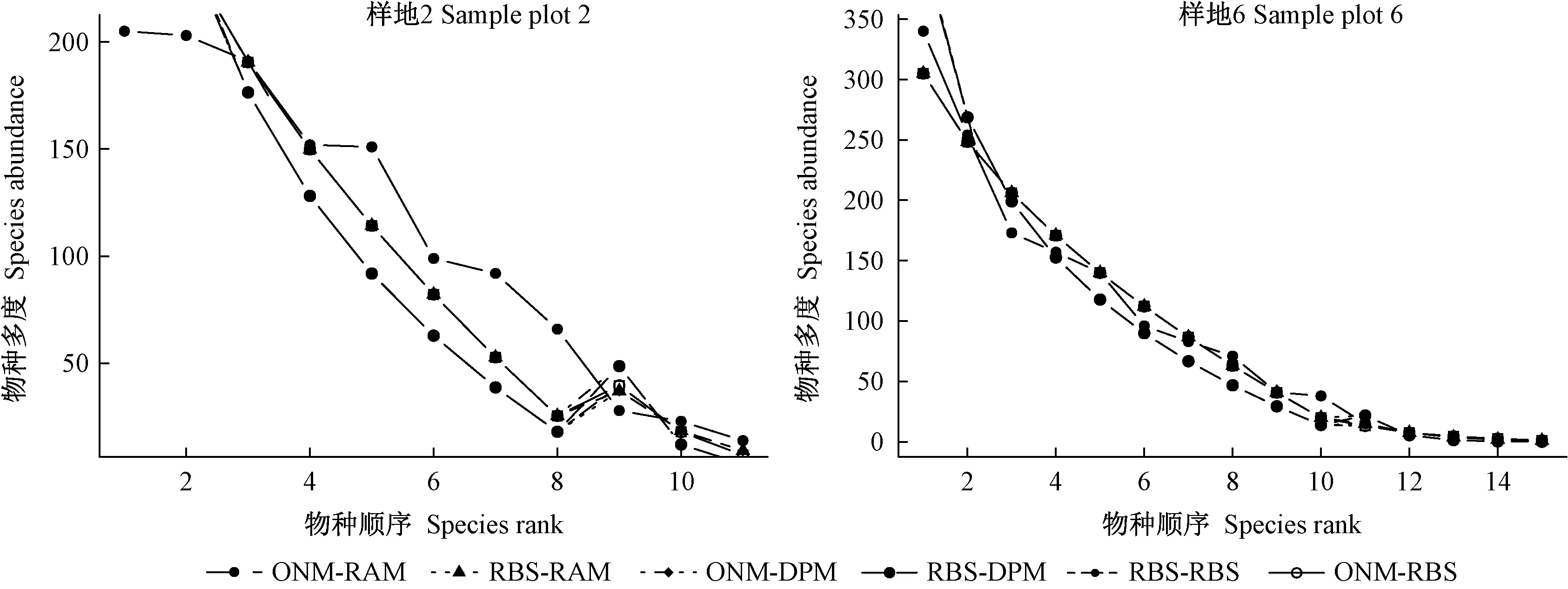
图4 6种复合模型拟合物种多度格局实例Fig. 4 Examples from the six kinds of composite model fitting to species abundance pattern

由表7可知，大多数群落陡变点的物种序号为8～10，表明云冷杉阔叶混交林是由7～10个物种组成的多优群落，这从表1中样地树种组成也可明显看到，优势种多度占整个群落多度的87%～99%，且多度分配较为均衡。不同数据集都以生态位重叠模型、随机分配模型、断棍模型和优势优先模型组合的复合模型拟合效果最佳，可见生态位重叠模型、随机分配模型、断棍模型和优势优先模型组合可能是云冷杉阔叶混交过伐林物种多度分布拟合的最佳复合模型。另外，复合模型检验指标除样地8外均通过拟合优度卡方和K-S检验，但χ2和D较生态位模型没有明显变化，AIC明显下降，表明复合模型拟合效果更好。由图4可知，复合模型的预测值与观测值更加接近，模型拟合的优良性有较大提高。2种模型的衔接部位可能会出现违背物种序列-多度关系曲线的现象(图4右图)，但由于陡变点前物种多度占总多度的87%～99%，因此这种拟合不会严重违背多度分布曲线。

表7 物种多度分布数据的复合模型拟合①Tab.7 Composite model fitting of species abundance distribution

3.6 断面积广义多度模型拟合

以胸高断面积作为广义多度指标进行群落物种多度格局拟合的结果如图5所示(以样地1为例)。

图5 断面积广义多度物种多度格局的经验统计模型、生态位模型、中性理论模型包络线检验和复合模型拟合(样地1)Fig. 5 Fitting of species abundance pattern for sample plot 1 basal area as abundance indices of different models

由图5可知，采用胸高断面积广义多度指标与采用数量多度指标进行群落物种多度格局拟合的经验统计模型、生态位模型拟合结果基本一致，但中性理论模型Volkov包络线检验拟合、复合模型表现与采用数量多度指标的相应模型截然不同，群落胸高断面积的多度分布更多表现为随机中性理论模型，复合模型的表现较单一模型差，尤其在陡变点附近，这可能是因为稀有种的数量多度所占比例虽然较低，但稀有种多数情况下在林分中为优势木或亚优势木，胸高断面积所占比例较高，胸高断面积的分配在各物种之间更加均匀，因此采用胸高断面积作为广义多度指标的复合模型拟合不能严格区分丰富种和稀有种，会导致竞争等级层次的模糊化或缺失化。

4 讨论

4.1 经验统计模型拟合情况

研究区云冷杉阔叶混交过伐林生境优越，种源丰富，林分异质性和多样性较高，为物种的抽彩式竞争奠定了基础，各物种多度分配较为均衡，优势种和稀有种数量均较少，大多数物种多度处于平均水平，采用对数正态模型拟合效果最佳，与赵志模等(1990)的研究结论一致。在拟合物种多度格局方面，泊松对数正态模型和对数正态模型拟合度一致，可采用对数正态分布去近似泊松对数正态分布(Blissetal.， 1953)。在参数相关性方面，对数级数模型参数T和对数正态模型参数λ与群落Marglef丰富度指数和Pielou均匀度指数具有明显相关性，表明这2个参数能较好反映群落物种丰富度和物种多样性(马克平等， 1997； 任萍等， 2009)。

4.2 机制模型拟合情况

相较于经验统计模型，生态位模型更能反映生境优越度(高利霞等， 2011)、异质性(刘梦雪等， 2010)、群落演化历史、物种组成的丰富程度、物种资源占据能力(彭少麟等， 2003)、生态位空间动态及其等级多度分布(Tokeshi， 1990)，可能是反映群落多度与资源分布正、负或无相关的更好模型(韩大勇等， 2014)。复合生态位模型认为群落物种多度格局不止遵循1种规律，最可能出现的情况是几个多度最大的种符合生态位分割模型，而其余多度较小的种符合随机分配模型(Tokeshi， 1990)。长白山云冷杉阔叶混交林资源丰富，丰富种多度配置较为均衡，采用断棍模型和生态位重叠模型拟合效果最佳，复合模型中生态位重叠模型在丰富种多度拟合时也表现最佳，稀有种所占比例较少，且多度分配是随机的，采用随机分配模型、断棍模型和优势优先模型拟合效果较好，其中尤以随机分配模型最佳，与Tokeshi(1990)预测基本一致。

复合生态位模型对丰富种(数据集1)和稀有种(数据集2)2个多度等级的分段拟合效果较单一模型好，表明丰富种和稀有种2个竞争等级在群落结构构建机制方面存在差异。前者更加符合重叠生态位理论，后者更加符合随机生态位分配理论，说明丰富种和稀有种在群落装配中属于2种机制，前者体现了生态位模型的确定性机制，后者体现了随机性机制，2种机制在过伐林群落构建中是共存的。物种相对频次分布曲线由丰富种和稀有种2部分组成(Frontier， 1985)，Magurran等(2003)在研究鱼类群落时也发现丰富种和稀有种(文中称为持久种或核心种和机会种)的群落构建经验统计模型存在差异，证明了群落构建的等级机制。随机分配模型认为物种生态位分配是非等级物种多度分布格局的动态变化(Tokeshi， 1990)，这可能是其在群落整体拟合中表现较差(图2)、在稀有种拟合中表现较佳(图4)的原因之一。另外，采用群落中性理论Volkov模型对过伐林物种多度格局进行拟合虽然通过检验，但其拟合表现稍逊于生态位模型，可见生态位过程在群落构建中的重要作用，而稀有种的生态位随机分配可能成为群落中性理论的弱化表现，中性理论被认为是当种间适应性无差异且无稳定生态位分化时的特例(Bar-Massadaetal.， 2014； Matthewsetal.， 2014)，Hubbell(2001)采用数学理论证明对数级数分布是零和多项式模型的一个特例，这些研究表明经验统计模型和机制模型并不是孤立的，任何群落都是群落连续体理论的一个“点”，采用复合模型分析可能阐释群落构建的生态位和中性理论机制过程在群落多度格局方面的体现，成为揭示各模型连续性的数学途径。

胸高断面积广义多度拟合实际上是传统物种多度格局的加权拟合方法，其权重为各物种平均胸径的平方，即将林木大小指标作为权重实现对物种多度格局的量化分析，拟合结果与传统物种多度格局拟合虽存在差异，但未能总体改变物种多度格局的分配情况。胸高断面积作为森林生产的功能指标(Picardetal.， 2002)，可能更加有利于进行森林功能多样性分析，扩展物种多度格局的功能特性阐释。

本研究的复合模型组成机制可能略有违背物种序列-多度原则，尤其是陡变点之后1～2个物种的多度可能超过陡变点物种的多度(图5)，这可能与随机分配、优势优先和断棍3种模型在稀有种拟合方面给第一物种优先分配更多多度有关，其改善可能需要提出更为恰当的机制模型。

4.3 过伐林物种多度分布成因分析

干扰是塑造群落结构、影响群落装配过程的重要因子(Podlaski， 2017)，林分过伐干扰后形成断层，先锋物种随机侵入，萌生物种原位更新，二者很快进入主林层，并与残留林冠层形成共优群落，随机干扰采伐事件的空间多尺度性和时间离散性增加了群落异质性和多样性(Podlaski， 2010)，种源扩散、物种竞争、森林采伐、随机干扰等多种机制共同构建了过伐林群落。研究区云冷杉阔叶混交过伐林目前处于恢复演替阶段，林分异质性为多物种侵入和生态位占据能力奠定了基础，各物种多度均衡的生态位模型如生态位重叠模型更能较好拟合当前群落状态，而到达演替顶极阶段，群落物种组成和数量比例趋于稳定，种间竞争等生态位过程并不明显(闫琰等， 2012； 张姗等， 2015)，物种多度差异较大的随机生态位模型或中性随机理论模型则可能占据主导(施建敏等， 2015； 任萍等， 2009； 徐国瑞等， 2017)，有利于群落定向演替的发生发展。姚兰等(2016)研究发现，干扰机制下萌生物种是影响群落物种多度格局的重要因素，过伐状态下萌生树种的大量出现(如紫椴、色木槭等)可能也是导致群落物种多度分布均衡的机制。先锋物种迅速侵占采伐迹地和快速生长进入主林层的本领(张会儒等， 2008)，是当前林分物种多度分配较为均衡的重要原因。残留林冠层的衰老、枯立、风倒机制和更新层的替代占位、竞争机制也是决定过伐林群落物种装配状态的重要生态过程(Kraftetal.， 2008)，2种以上的生态位过程机制在决定群落装配中发挥重要作用(Hollingsworthetal.， 2013)。

关于长白山温带森林群落的多数研究认为，群落生境优良，同质性高，环境因子的过滤筛选作用较低，种间作用并不强烈，表现为随机生态过程占据主导，扩散限制作用较高(Zhangetal.， 2009； Yuanetal.， 2011； Wangetal.， 2011)，而生态位作用较低(张姗等， 2015)。本研究对过伐林群落多度格局过程的分析表明，云冷杉阔叶混交过伐林群落处于恢复演替阶段，高生境异质性和干扰事件随机性分别决定了生态位理论和中性理论2种机制在过伐林群落构建中的作用，同时受扩散机制、生态位竞争、干扰过程等影响，过伐林多优群落处于均衡多度分布格局中，演替后期云杉、冷杉和顶极伴生种的物种比例与演替前期阔叶树种的比例相当，演替顶极针叶树种红松受种源限制很少出现，东北红豆杉、黄蘗(Phellodendronamurense)、胡桃楸(Juglansmandshurica)、花楸(Sorbuspohuashanensis)、朝鲜槐等稀有种的物种多度较少，这可能是由于过伐林与长白山温带森林处于2个不同的发育阶段，过伐林处于演替恢复期，生态位过程占据主导，稀有种的多度和频度均较少，而长白山温带森林处于原始演替顶极状态，中性随机理论模型占据主导(Wangetal.， 2011)，演替后期的稀有种和伴生种比例较高。在过伐林群落次生演替中，喜寒凉气候的暗针叶树种与喜温凉湿润气候的阔叶树种因资源利用、环境适应、干扰应变等方面的差异而在群落中同时存在，且表现出普遍生态位重叠(伏捷等， 2018)，但重叠程度较低(邹春静等， 2001)，这也可能是塑造过伐林物种多度均衡的重要机制。

多数研究表明，物种多度格局受尺度(张忠华等， 2012； 程佳佳等， 2011)、物种空间分布格局(王绪高等， 2008)等的影响。Wang等(2018)对吉林蛟河温带林的研究发现，大树周围总是被异种的大树所围绕，这也可能是制约物种多度格局均衡分配的主要因素。中性理论模型在大尺度(程佳佳等， 2011； 闫琰等， 2012； Fisheretal.， 2014； Chengetal.， 2012)和物种多样性较高群落(Chisholmetal.， 2010)拟合方面往往较生态位模型表现更好，本研究并未发现该规律。下一步将开展物种空间分布格局与物种多度格局的尺度关联研究，建立空间明确的多尺度物种多度格局模型，阐明不同尺度上控制格局的生态过程和机制，揭示物种空间分布与多度格局之间的关系。

4.4 过伐林经营意见

上述群落物种多度格局分析表明，长白山云冷杉阔叶混交过伐林群落处于恢复演替阶段，通过经营干预可有效减少其演替发育时间。针对林分特点，在过伐林经营中要注意以下几点： 1) 减少先锋软木阔叶树种比例，增加伴生硬木阔叶树种比例； 2) 通过林下补植提高红松比例，间伐林冠上层减少云冷杉比例，提高目标树单木生长量，减弱风倒危害，影响云冷杉更新层，降低云冷杉聚集规模； 3) 保留部分上层霸王木、老狼木，保留和促进珍贵树种如东北红豆杉和三大硬阔的更新； 4) 采用近自然经营方法(陆元昌等， 2011)、森林生态系统采伐技术体系(张会儒等， 2008)、可变绿树保持法(Maríaetal., 2011； Laurenetal.， 2013)，使云冷杉阔叶混交林林分逐步向红松云冷杉林过渡，促进结构发育的多层性、异质性和复杂性，稳定和提高林分多样性和生产力，提升林分的健康稳定性。

5 结论

1) 经验统计模型中对数正态模型和泊松对数正态模型拟合效果最佳，对数级数模型拟合效果较差，对数级数模型参数T和对数正态模型参数λ可作为表征群落多样性的重要参数。

2) 生态位模型中断棍模型拟合效果最佳，其次是生态位重叠模型和几何级数模型，再次为Zipf模型和Zipf-Mandelbrot模型，最后为随机分配模型和优势优先模型。

3) 复合生态位模型在物种多度分析中拟合效果较传统生态位模型有较大提高，复合模型可能在群落丰富种和稀有种呈现竞争等级多度分布时拟合效果最佳。

4) 复合模型可能成为连接经验模型、生态位模型和中性理论模型的纽带，为研究物种多度格局提供数学途径和思路。

5) 以胸高断面积为指标的物种多度分布拟合与以个体数为指标的经验统计模型和生态位模型物种多度分布拟合表现基本一致，而在群落中性理论模型和复合模型拟合表现方面有一定差异，可能与稀有种断面积比重较大有关。

6) 云冷杉阔叶混交过伐林群落物种等级多度分布某种程度上是生态位过程和随机干扰生态过程共同作用的结果。