一种航空发动机压气机喘振检测方法

申世才，雷 杰，郝晓乐

(中国飞行试验研究院发动机所，西安，710089)

喘振是一种危害性极大的发动机压缩系统气动失稳现象，轻则造成发动机工况急剧恶化,重则导致发动机机械损伤，进而引发严重飞行事故，引起人员和财产的巨大损失[1]。因此，寻求一种快速、准确检测发动机喘振故障的方法是发动机稳定性研究领域的热点问题，对于保障航空器飞行安全具有重要的现实意义和价值。

当前，国内外的喘振检测方法基本是以压气机出口流场压力为对象，根据压力信号时域或频域特征进行喘振算法研究。其中基于压力信号时域特征的喘振检测算法主要有：自相关函数法[2]、短时能量法[3]、变化率法[4-5]、压差法[6]、方差分析法[7]、统计特征法[8]等，基于压力信号频域特征的喘振检测算法主要有：频谱分析法[9-11]、小波分析法[12-13]、频域幅值法[14-15]等。上述时域和频域特征喘振检测算法多数是以压气机部件级试验为支撑，取得了很多较好的喘振检测效果，但由于受到试验对象和条件限制，应用在发动机整机喘振检测的算法相对较少，有必要寻求一种简单、可靠、准确的发动机整机喘振检测方法。

1 压气机出口脉动压力统计特征分析

发动机压气机出口动态压力p31包含平均压力成分p31.a和脉动压力成分Δp31，在发动机稳定状态下，压力机内部流场稳定，其出口脉动压力Δp31相对稳定，而在发动机出现喘振时，压气机出口流场Δp31呈不稳定状态[4]。所以当发动机稳定工作时，如果Δp31服从某种概率分布规律，根据其概率分布函数，就可以通过Δp31的统计特征设置阈值来检测发动机喘振故障的发生。

正态分布是统计学中最重要的一种分布规律，大量随机现象可以用正态分布规律来描述或近似，同时正态分布具有很多优良的性质，所以不论是在理论研究还是工程实践中，正态分布具有广泛的应用。这里首先假设Δp31测量数值服从正态分布，下面采用某发动机实测数据检验压气机出口脉动压力时间序列数据是否符合正态概率分布规律。

某发动机试飞期间，测量了不同飞行高度、速度条件下发动机稳态及瞬态的p31时间序列数据，获取了相应的Δp31时间序列数据。将这些不同飞行条件下发动机稳态和瞬态Δp31时间序列数据作为总体统计量，采用简单随机抽样原则从总体统计量中抽取发动机稳态和瞬态Δp31时间序列数据作为检验样本，进行Δp31时间序列正态符合性检验分析。

样本数据x的正态性检验方法有很多，主要分为统计图法和统计指标法。统计图法包括直方图、P-P图、箱式图、概率图、分位数图等，均能为样本正态性提供一个粗略估计，本文采用分位数图对样本Δp31正态性进行初步估计；统计指标法可对样本正态性进行定量检验，主要包括偏度峰度联合检验、S-W(Shapiro-Wilk)检验、A-D(Anderson-Darling)检验、K-S(Kolmogorov-Smirnov)检验等，本文选择K-S检验作为样本Δp31的正态性定量检验方法。

图1为高压转速为n2时发动机稳态过程Δp31时间序列随机样本分位数图，可见该发动机稳态输入样本散点不完全分布在直线附近，故而不能完全为正态分布提供粗略支持，进一步采用K-S检验。

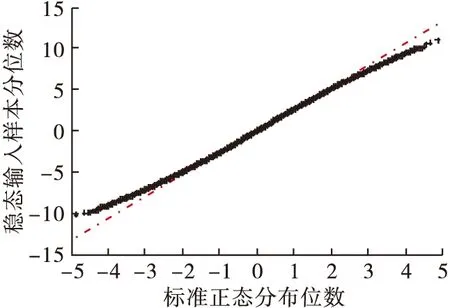
图1 稳态过程时间序列样本数据分位数图

K-S检验统计量为：

Dn=max{|Fn(xi)-F0(xi)|,|Fn(xi+1)-F0(xi)|}

(1)

式中：Fn(x)为样本的概率分布函数；F0(x)为标准正态分布函数。如果检验统计量Dn大于给定显著水平α和样本容量n确定的检验临界值Dn(α)，则拒绝零假设，否则接受零假设，认为Δp31符合正态分布。

对图1中发动机稳态过程时间序列样本Δp31进行计算，得到Dn=0.008 3，取显著性水平α为0.01时，查表得到临界值Dn(α)=0.002 5，Dn>Dn(α)，故拒绝零假设，所以发动机稳态过程Δp31不服从正态分布。

进一步分析发动机瞬态过程Δp31是否服从正态分布，图2为发动机瞬态过程Δp31随机样本分位数图，显然发动机瞬态过程Δp31输入样本散点同样不完全分布在直线附近，进一步进行K-S检验：Dn等于0.014 7，取显著性水平α为0.01时，查表Dn(α)为0.004，Dn>Dn(α)，拒绝零假设，故发动机瞬态过程Δp31同样也不服从正态分布。

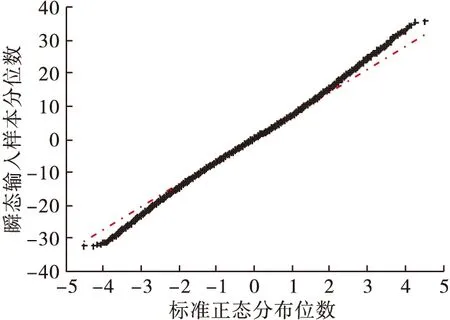
图2 瞬态过程时间序列样本数据分位数图

进行全部Δp31时间序列样本正态符合性检验后，发现Δp31不服从正态分布，这是因为发动机压气机是高温、高速旋转机械部件，其Δp31信号包含了发动机转子频率、叶片频率的基频和倍频成分及受发动机瞬态过程影响，其测量数据随时间统计序列不服从正态分布，所以对于Δp31这种未知分布规律，难以根据其统计特征设置喘振检测阈值，想要Δp31按正态分布设置喘振检测阈值，必须将Δp31时间序列样本数据进行正态转换。

2 压气机出口脉动压力正态转换

2.1 Johnson正态转换方法

常用的非正态数据正态转换方法主要包括：倒数转换、对数转换、平方根转换、平方根反正旋转换、平方根后取倒数转换、Johnson转换等，其中前5种方法对样本数据的要求较高，要求样本x为正值，由于Δp31存在负值数据，故难以采用前5种转换方法对Δp31数据进行正态转换。

Johnson转换条件相对宽松，允许样本x存在负数的情况，具有良好适应性且Johnson转换可将随机样本x直接转换为标准正态分布N(0,1)。本文采用Johnson转换方法对Δp31时间序列样本数据进行正态变换。样本x进行Johnson正态转换时，其基本转换公式为：

z=γ+ηf(x,ε,λ)

(2)

式(2)中f(x,ε,λ)为特定Johnson分布曲线函数，具体为SB(有界)、SL(对数正态)、SU(无界)3种类型，η、γ、λ、ε等通过对应转化类型计算公式得到，3种类型函数及参数约束条件见表1。

确定Johnson转换函数的方法有很多，其中样本百分位数法得到了广泛应用，本文采用百分位数法进行正态转换。

首先选择一个合适的r,在标准正态分布表中查找(-sr，-r，r，sr)的分布概率P-sr、P-r、Pr、Psr，通过样本获取对应分位数x-sr，x-r，xr，xsr后，计算m=xsr-xr、k=x-r-x-sr、l=xr-x-r，得到分位数比mn/l2。

当mk/l2<1时为SB分布，mk/l2=1时为SL分布，mk/l2>1时为SU分布。由于分位数比与s和r取值有关，需要确定合适的s和r，研究表明s取值为3及r取值范围为(0.25，0.26，…，1.25)时，可获得较好的转换效果[16-17]。

本文取r值为1.2(在0.25～1.25范围内，r取值1.2时正态转换效率最高)，对于图1和图2中发动机稳态和瞬态过程随机样本，计算得到mk/l2值分别为0.721和0.921 5，即mk/l2<1，Δp31的Johnson转换函数为SB型，对应的η、γ、λ、ε计算公式为:

(3)

(4)

(5)

(6)

2.2 Johnson正态转换结果

采用K-S方法对正态转换后的脉动压力时间序列样本Δp31.norm正态性符合性进行检验。其中图1所示发动机稳态过程Δp31.norm检测结果为：Dn=0.001 1，Dn(α)=0.002 5，DnDn(α)，拒绝了零假设，故Johnson正态转换后的瞬态Δp31.norm不服从正态分布。

对其他随机样本采用Johnson转换并检测转换后Δp31.norm的正态性，发现Johnson转换方法对于稳态过程具有较高的转换效率，稳态过程Δp31.norm正态转化成功率P可达到90%以上，但是对于瞬态过程随机样本正态转换效果较差，瞬态过程Δp31.norm正态转化成功率P不足50%。

进一步分析瞬态过程Δp31正态转化率不足的原因：样本Δp31是时间序列的统计量，其受发动机状态变化影响很大，当发动机稳态工作时，Δp31幅值范围基本稳定在同一量级，而不同转速时Δp31幅值范围差异较大，且在瞬态变化过程中，随着发动机转速的提高，Δp31幅值变化范围也逐渐升高(具体如图3所示)，这种Δp31幅值随转速变化的特性是导致瞬态过程Δp31随机样本Johnson正态转化成功率P过低的主要原因。

为解决发动机瞬态过程Δp31正态转换成功率P过低问题，必须降低瞬态过程转速变化对于Δp31幅值变化范围的影响，考虑到样本Δp31是时间序列的高频采集信号，其采样频率为5 kHz，减小Δp31样本容量n就可以直接削弱转速变化对于Δp31幅值变化范围的影响，当样本容量n减小到一定程度时(如几十毫秒量级)，可假设认为发动机瞬态过程时间序列Δp31相当于一个准稳态变化过程。按照上述方法，逐步减小随机样本容量n，从总体样本抽取几十组发动机瞬态过程随机样本进行Johnson正态转换，正态转化成功率P统计情况见表2所示，可见减小样本容量n可有效提高瞬态过程Δp31的正态转化成功率，当随机样本量n降低至500及以下，随机样本Δp31的Johnson正态转换成功率达到90%以上，因此要实现瞬态过程Δp31有效正态转换，可将样本容量n确定为100。

表2 瞬态过程正态转化成功率统计表

3 喘振检测阈值和方法

3.1 喘振检测量

正态转换后的Δp31.norm～N(0,1)，根据其概率分布函数可知，Δp31.norm时间序列落在±3.5范围内的概率为99.95%，即Δp31.norm有99.95%概率分布在-3.5≤Δp31.norm≤3.5范围内，那么根据表1中SB型Johnson转换函数的反函数z-1，可以得到正态转换前Δp31的99.95%概率分布范围为：

(7)

由于瞬态过程Δp31样本容量n不宜过大，当n过大时将不能有效实现Δp31正态转换，所以也就不能通过Johnson转换函数的反函数z-1获取Δp31的99.95%概率分布范围。此外，不同发动机状态下Δp31幅值范围存在较大差异，导致其99.95%概率分布范围不同，进而不能根据Δp31分布范围使用固定喘振检测阈值。为解决这一问题，本文采用一种基于滑动窗口的Johnson转换方法，具体如下。

假设滑动窗口长度为d，将测取的发动机时间序列Δp31第1点数据x1作为滑动窗口起始点，向后截取d个Δp31数据。对窗口内d个Δp31数据进行Johnson正态转化，得到SB型Johnson正态转换函数反函数的η、γ、λ、ε等参数，根据公式(7)计算窗口内Δp31数据99.95%概率分布上界Δp31.max和下界Δp31.min。将Δp31.max、Δp31.min作为第xd点时间序列Δp31的99.95%概率分布上界Δp31.max(xd)和下界Δp31.min(xd)。按照Δp31时间序列顺序滑动计算窗口，重复上述计算方法，可以得到Δp31的99.95%概率分布的自适应上界Δp31.max和下界Δp31.min，实际等效于Δp31上下“包络线”。

样本容量n为100时正态转换成功率最高，取滑动窗口d=100，对于图3所示Δp31时间序列样本数据，其99.95%概率的Δp31.max、Δp31.min分布情况见图4所示，局部放大情况见图5，可见采用滑动窗口的Johnson正态转换方法，能够获取时间序列Δp31的99.95%概率分布自适应上界Δp31.max和下界Δp31.min。

上文所述Δp31等效“包络线”反映了其幅值变化范围，可以根据Δp31上下“包络线”间距D检测发动机喘振，为消除D受发动机转速变化的影响，定义一种无量纲的发动机喘振检测量T31为：

(8)

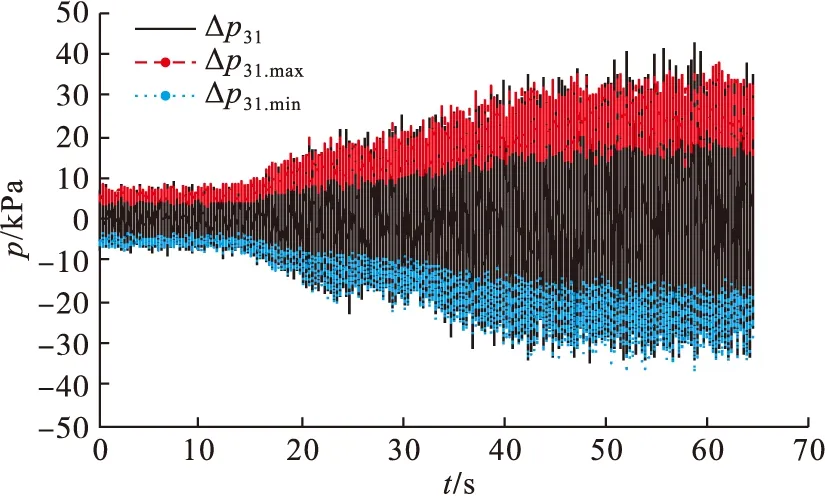
图4 脉动压力概率边界时间序列

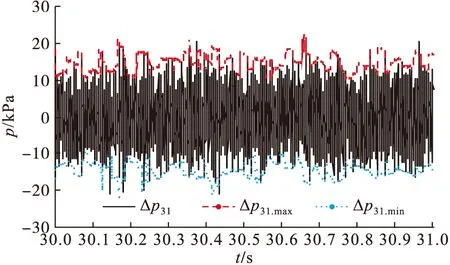
图5 脉动压力概率边界时间序列局部放大图

式(8)等效于对Δp31.max和Δp31.min间距D进行归一化处理，可以消除发动机不同转速时D幅值范围的差异，便于设置固定的喘振检测阈值。如对于图4中所示的Δp31时间序列，其对应的喘振检测量T31计算结果如图6所示。

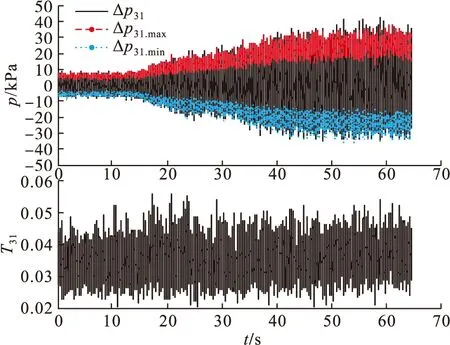
图6 发动机无量纲喘振检测量时间序列

3.2 喘振检测阈值及方法

设置发动机喘振检测阈值时，将上文不同飞行条件下发动机稳定工作时测取的稳态和瞬态时间序列Δp31作为总体统计量，采用滑动窗口的Johnson转换方法计算对应的喘振检测量T31，将获取的T31作为设置喘振检测阈值A的总体样本。

采用K-S方法检验总体样本T31正态性，表明其并不服从正态分布。对总体样本T31进行Johnson转换，即T31.norm～N(0,1)。对于转换后的T31.norm，其同样有99.95%概率分布在±3.5范围内，由公式(7)计算发动机稳定工作时T31变化范围为：

0.018 5≤T31≤0.079 8

(9)

因为当发动机喘振时，Δp31脉动幅值会迅速增大，其概率意义“包络线”间距D必然会出现剧增，那么T31将不可避免超出0.079 8的范围，可以设置固定喘振检测阈值A=0.079 8。但是发动机稳定工作时，T31还存在0.025%概率小幅超过0.079 8，所以综合考虑喘振检测灵敏度和误报率，引入一个优化参数t(1≤t≤2)，设置保守的固定喘振检测阈值为：A=0.079 8t，t根据实际喘振检测效果设定，以最低喘振误报率作为t取值依据。

综上所述，根据发动机固定喘振检测阈值A，本文设计的喘振检测方法为：当喘振检测量T31大于A时，认为发动机出现喘振；当T31小于等于A时，认为发动机工作稳定。

4 喘振检测方法试验验证

某发动机试飞期间先后发生3起喘振故障，其中地面发生喘振1次，空中发生喘振2次(记为空中喘振1、空中喘振2)，地面发动机喘振发生在稳态过程中，空中2起喘振分别发生在加速、减速过程中，使用该型发动机喘振试飞数据对喘振检测方法的实际效果进行试验验证。

图7～9为该发动机3次喘振检测验证结果，3次喘振检测均发出了喘振信号。当发动机稳定工作时，不管是稳态过程还是瞬态过程，喘振检测量T31变化幅值均相对稳定，不受发动机转速变化影响，T31没有超过检测阈值A的范围，而当发动机出现喘振时，喘振检测量T31值会出现剧增并超过检测阈值A。图7所示发动机稳态过程，喘振时，从脉动压力Δp31出现波动到发出喘振信号用时约为12 ms，喘振期间T31最大值增长至1.748；喘振消失时，从脉动压力Δp31停止波动到喘振信号消失用时约为14 ms。图8、图9所示发动机瞬态过程，喘振时从脉动压力Δp31出现大幅波动到发出喘振信号用时分别约为16 ms、15 ms，喘振期间T31最高增长到1.653和1.689；喘振消失时从脉动压力Δp31停止波动到喘振信号消失用时分别约为17 ms、14 ms。

综上所述，本文发动机喘振检测方法成功检测出3次喘振故障，其识别发动机喘振及退出喘振所需时间均小于20 ms，未出现虚警、漏报等异常情况，验证了检测方法的有效性和准确性，表明方法具有识别率高、报警迟滞小等优点。

图7 发动机地面喘振检测结果

图8 发动机空中喘振1检测结果

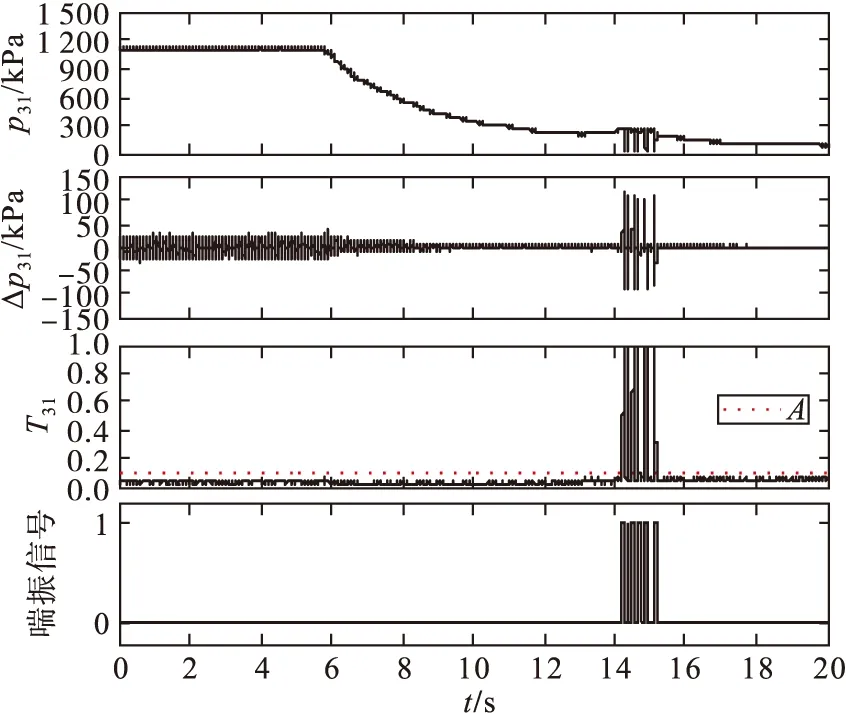
图9 发动机空中喘振2检测结果

5 结论

1)在地面及空中发动机稳定工作时，压气机出口脉动压力不服从正态分布。对于稳态过程脉动压力，采用Johnson方法的正态转换成功率较高，可达90%以上，但是对于瞬态过程正态转换效果较差，当样本容量n降低至500以下时，瞬态过程脉动压力正态转化成功率可达到90%以上。

2)采用滑动窗口的Johnson转换方法，可以获取压气机出口脉动压力99.95%概率分布的自适应上边界和下边界。在不同发动机转速下，该上、下边界距离的幅值范围差异较大，且随发动机转速增大而增大。

3)在地面及空中发动机稳定工作时，提出的喘振检测量消除了发动机状态变化带来的影响，在稳态及瞬态过程中变化范围差异很小，即喘振检测量不受发动机工作状态变化的影响。

4)根据喘振检测量能够设置适应发动机任意状态的固定喘振检测阈值，通过3次喘振试飞数据的验证，其识别发动机喘振及退出喘振所需时间均小于20 ms，表明喘振检测方法具有识别率高、报警迟滞小等优点。