软扩频多址信号盲分离

张丹娜, 闻年成, 刘中飞, 杨晓静

(国防科技大学电子对抗学院,合肥，230037)

Walsh码软扩频技术是直接序列扩频技术和编码技术的结合[1]。对于(n,k)Walsh码软扩频信号而言，实质是将k比特信息按照某种对应关系映射到一组n比特伪随机码中的一个，其中伪随机码采用Walsh码。现今，Walsh码软扩频技术在外军Mark Ⅶ Mode 5敌我识别系统[2]、挪威新一代战地通信网[3]、无线通信[4]等通信领域中广泛应用。信号在传输过程中，不可避免地会叠加其它用户发射的软扩频信号，接收端接收的软扩频信号会受到多址信号干扰，所以须将多用户信号分离并对分离后的信号进行解扩才能获取接收信号中有用的信息。因此，研究Walsh码软扩频多址信号盲分离具有重要意义。

文献[5]采用主分量分析结合独立分量分析算法实现多径多址直扩信号盲分离，然后采用三阶相关函数提取直扩信号的伪码序列，该算法最多实现3位用户盲分离以及伪码序列估计。文献[6]对多址多径DS-CDMA信号采用特征值分解，获取用户特征向量子空间，通过二维Givens矩阵对特征向量矩阵构成的矩阵进行旋转，当旋转矩阵方差最小时，得到最佳估计伪码序列。现有文献大多是针对直接序列扩频多址信号盲分离的。同一用户传输的软扩频信号每比特信息对应不同的伪码序列，不同用户传输的软扩频信号每比特信息也对应不同的伪码序列。但对于直扩信号而言，同一用户传输每比特信息对应相同的伪码序列，一般直扩多址信号盲分离算法难以估计软扩频多址信号采用的多个伪码序列。因此，上述直接序列扩频多址信号盲分离算法难以实现软扩频多址信号盲分离。现有文献尚未发现对Walsh码软扩频多址信号盲分离的研究。

本文根据多用户之间信号相互独立的特点，建立了适合软扩频多址信号盲分离的模型，实现软扩频多址信号盲分离以及伪码序列估计。采用多接收端接收软扩频多址信号的方法。在暂不考虑多径效应的前提下，首先根据已知伪码速率和伪码周期对接收数据进行采样分组，然后利用主分量分析(Principal Component Analysis, PCA)算法对分组信号进行降维白化，最后采用Fast-ICA算法实现多址信号盲分离，并估计被分离信号的伪码序列。Matlab仿真结果表明，本文算法能够在一定信噪比范围内实现不多于5位用户的Walsh码软扩频信号盲分离并估计出被分离信号的伪码序列。

1 Walsh码软扩频建模

1.1 单用户Walsh码软扩频模型

(n,k)Walsh码软扩频发射端模型见图1。

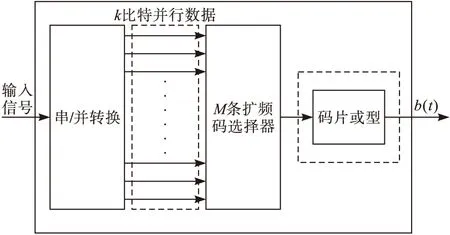
图1 单用户软扩频信号发射端模型

将输入信号记为d(t)，信息码d(t)经过串并转换后得到多组并行数据，每组并行数据含有k比特信息。并行数据共有M=2k个状态，每组并行数据根据自身的状态从n条Walsh码序列中选取M条伪码序列传输信息。

M条扩频码选择器输出多组并行数据，每组并行数据含有n比特传输信息。由图1可以看出，软扩频系统进行了(n,k)编码，将k比特信息映射到n比特传输数据。和直扩信号相比，软扩频系统的伪码序列有M=2k种，直扩系统的伪码序列仅有M=1种。若采用直接序列扩频多址信号盲分离算法，仅能估计一种伪码序列。因此，直接序列扩频多址信号盲分离算法不适用于软扩频多址信号盲分离。

设传输的信息数据为：

(1)

式中：an=±1；Tb为信息码元宽度；gb(t)是幅度为1且长度为1的矩形波。

将信息码元按k比特分组，则分组信息码可以表示为：

(2)

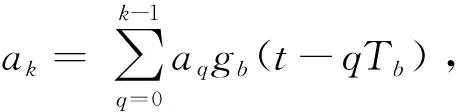
k比特信息码权值为：

(3)

k比特信息码元根据计算的权值j从n条Walsh码序列中选取M条伪码序列传输信息。软扩频接收系统可以表示为：

(4)

式中：Cj是由信息码的权值j确定。信息数据通过高斯白噪声信道后，接收到的软扩频信号可以表示为：

(5)

式中：w(t)是均值为0，方差为1的高斯白噪声，并且与b(t)相互统计独立.

1.2 多用户Walsh码软扩频模型

图2为多用户(n,k)Walsh码软扩频信号传输模型。图2中单用户软扩频发射端为图1所示的单用户(n,k)Walsh码软扩频发射端模型，每位用户选用的扩频码序列选择器为Walsh码产生器。

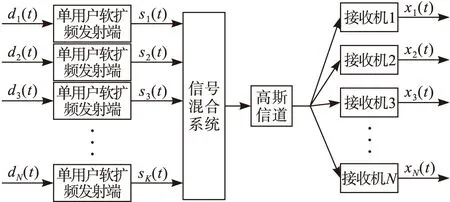
图2 多用户软扩频信号传输模型

K位用户需要传输的信息经过(n,k)软扩频编码处理后发射到空中，信号在传输过程中不可避免地叠加了其他用户信息。图2中信号混合系统表示多用户信号按照某种规则叠加，用N×K维矩阵A表示信号混合矩阵，Z=AS表示叠加后的混合信号。接收端接收的信号被多址信号和高斯白噪声干扰，数学表达如式(6)所示：

X=AS+w(t)

(6)

式中：X=[x1(t),x2(t),…,xN(t)]T；S=[s1(t),s2(t),…,sK(t)]T；N表示观察端总数；K表示用户总数；AN×K表示信号混合矩阵；w(t)表示信道传输中叠加的高斯白噪声。

2 软扩频盲分离算法

2.1 软扩频多址信号预处理

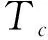
(7)

将式(7)写成矩阵形式，如式(8)所示：

(8)

其中：

rji(m)=[r(ij),r(ij+1),…,r(ij+n-1)]T

(9)

式中：j表示第j个接收端接收的数据，i表示每个接收端的第i个分组。

取每个接收端第i组数据为观测向量，记为：

(10)

计算观察向量的相关函数为：

(11)

对观测向量进行特征值分解：

(12)

式中：Us为n×n的信号子空间；Un为(N-n)×(N-n)噪声子空间；σ2是高斯白噪声的方差。对采样得到的向量进行降维白化，以消除信号之间的相关性。

根据文献[7]可知，白化矩阵为：

(13)

数据经过降维白化后，得到观察向量如式(14)所示：

(14)

2.2 Fast-ICA算法

Fast-ICA算法是由Hyvärinen及其合作者[8-12]提出的一种基于负熵最大化的固定点批处理ICA算法。算法具有计算简单，收敛速度快等特点，在实际工程中被广泛使用[13-20]。

该算法从中心极限定理出发，认为多个独立随机变量的混合信号趋近于高斯分布。接收的软扩频多址信号是多个独立信号的线性组合，因此接收信号中任一分量的高斯性都比源信号强，通过极小化接收信号的高斯性可以分离出多用户信号。Fast-ICA算法采用负熵作为混合信号非高斯性的度量，负熵越大，其非高斯性越强。信息最大化准则是Fast-ICA算法另一个重要的独立性判据。该准则认为每个非高斯局部极大值对应着一个独立分量，求解独立分量可以理解为寻找极大非高斯变换。当接收混合信号的负熵取得极大值时，标明完成独立信号的分离。但每次分离出的源信号无法预先确定，为避免重复分离同一源信号，在下次分离源信号需要将之前把已经提取的独立分量去掉。

Fast-ICA算法虽能实现信号的盲分离，但分离出的信号具有幅度不确定性和次序不确定性。幅度的不确定性主要体现在分离信号的幅度发生改变，使得估计的伪码序列幅度和实际伪码序列幅度不符；次序的不确定性主要体现在多次盲分离后，相同用户发射信号的位置不一致。幅度的不确定性可以通过设定合适的阈值进行数值判断来消除。次序的不确定性可以根据本次提取的独立分量与上次提取独立分量的互相关系数大小重新排列分离后的各个分量[21]。或者比较处理后的各独立分量的概率分布，将分布最为相似的独立分量归为同一个源信号发出的信号[22]，由此对分离后的各独立分量进行重新排序[23]。

基于Fast-ICA算法，软扩频多址信号盲分离问题转化为寻找正交矩阵W，使得WTX非高斯性最大,即负熵最大，然后逐个分离出多个独立信号，其中X为观测数据。

由于本文篇幅有限，这里对Fast-ICA算法的推导过程不做赘述，仅给出算法的基本步骤：

步骤1观测数据X中心化处理，Xi=Xi-E(Xi)，使得观测数据的均值为0。

步骤2X→Z，观测数据降维白化。

步骤3初始化wp为一单位长度的随机向量。

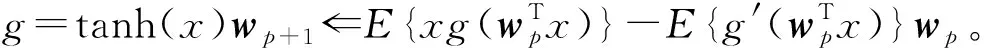
步骤5wp⟸wp/‖wp‖，正交化处理。

步骤7利用得到的正交矩阵获得源信号，Y=WTZ。

2.3 算法步骤

根据2.1节和2.2节对Walsh码软扩频多址信号预处理以及Fast-ICA算法的描述，本文建立适用于软扩频多址信号盲分离的模型，采用多个接收端接收数据并用主分量分析算法消除信号的相关性，然后采用Fast-ICA算法实现Walsh码软扩频多址信号盲分离。Walsh码软扩频多址信号盲分离算法步骤如下所示：

输入：接收的Walsh码软扩频多址信号。

输出：混合信号中用户数量以及多址信号采用的伪码序列。

步骤1根据已知伪码周期和码片速率对接收数据进行采样分段，生成分段矩阵X(n)。

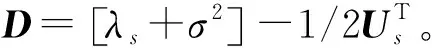
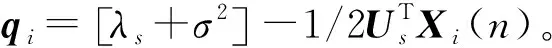
步骤4对观察向量进行中心化处理，qi=qi-E(qi)，使得观察向量的均值为0，便于后续正交矩阵的计算。

步骤5令p=1，初始化wp为一单位长度的随机向量。

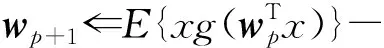
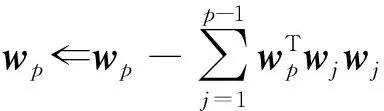
步骤8对wp做归一化处理，wp⟸wp/‖wp‖。

步骤10利用得到的正交矩阵W获取软扩频多址信号用户数目以及每位用户使用的伪码序列，Y=WTq。

3 仿真结果

为了验证上述算法能够实现软扩频多址信号盲分离，本文采用Matlab软件进行仿真实验，验证本文算法实现软扩频多址信号盲分离以及伪码序列估计，仿真研究软扩频多址信号盲分离性能以及用户数目对盲分离性能的影响。

3.1 实验1：Fast-ICA算法实现软扩频信号分离伪码序列估计

仿真参数：每个用户采用(8，3)Walsh码软扩频编码，用户数为4，观察端数目为4，信噪比SNR=10 dB，接收信号比特数为1 600 bit。仿真结果见图3～5。

图3 接收端接收的观察向量

图4 Fast-ICA算法多径信号分离和伪码序列估计

图5 实际多径信号数目以及伪码序列

图3为接收端接收信号经过采样分组之后的数据。图4为分组信号经过Fast-ICA算法分离出的信号数目以及估计的伪码序列。为便于观察，分离后的信号以0为阈值，大于0的记为1，小于0的记为0。图5为实际多用户采用的伪码序列。由图4和图5对比可知，Fast-ICA算法能够估计出信号源的数目为3。通过一一对比分离后的信号序列和实际信号序列可知，分离之后信号的次序被打乱，与接收信号源的次序不对应，后续可利用同一信号源发射信号具有相关性对分离信号重新排序。同时，由于Fast-ICA盲分离算法具有分离信号幅度不确定性，图4中分离信号2、3和4与实际信号4、1和2相比，幅度完全相反，与Walsh码矩阵比对，可以将幅度取反的信号恢复，恢复后的信号与实际信号一致。由分析可知，Fast-ICA算法在SNR=10 dB时，可以实现(8，3)Walsh码软扩频多用户信号盲分离，并且估计出用户采用的伪码序列。

3.2 实验2：Fast-ICA实现Walsh码软扩频多址信号盲分离性能

仿真参数：每位用户采用(8，3)Walsh码软扩频编码，用户总数为2，信噪比取值范围在11～20 dB之间，接收信号比特数为1 600 bit，每个信噪比环境下进行500次实验。图6为Fast-ICA算法实现Walsh码软扩频多址信号盲分离性能曲线图。由分析可知，随着信噪比的提高，算法对于Walsh码软扩频多址信号的分离性能有所提升。在信噪比为20 dB时，算法准确分离信号的概率达到97%，在信噪比为11 dB时，算法准确分离多址信号的概率接近62%。由Matlab仿真结果可知，Fast-ICA算法实现Walsh码软扩频多址信号盲分离的性能随着信噪比的升高有所提高，且变化较为显著。

图6 Fast-ICA软扩频多址信号盲分离性能

3.3 实验3：用户数目对Fast-ICA实现多址信号分离性能影响

仿真参数：每位用户采用(8，3)Walsh码软扩频编码，信噪比取值范围在15～20 dB之间，接收信号比特数位1 600 bit，每个信噪比环境下进行500次实验。图7为用户数目对算法性能的影响。

图7 用户数目对算法盲分离性能影响

图7中用不同的符号标识算法实现不同用户数目盲分离的性能曲线。由于Fast-ICA算法中采用牛顿迭代法，随着信号源数目的增加，算法的迭代次数增加，收敛速度降低，Walsh码软扩频多址信号分离性能降低。由图7可知，随着用户数目的增加，改进Fast-ICA算法对Walsh码软扩频多址信号盲分离的准确概率下降，实验结果与理论分析一致。用户数目少于4位时，在一定信噪比范围内，算法盲分离性能最佳，当用户数目大于等于4位时，算法盲分离性能随着用户数目的增加而降低，当用户数目为6，SNR≤11 dB时，算法难以实现软扩频多址信号盲分离，无法准确估计用户数量以及伪码序列。分析可知，Fast-ICA算法在一定范围内实现不多于5位用户信号的盲分离。

4 结语

本文采用Fast-ICA算法实现软扩频多址信号盲分离，并估计用户数量以及用户使用的伪码序列。算法首先根据已知伪码周期和伪码速率对接收端的信号进行采样分组，得到观察向量，然后采用主分量分析算法对观察向量降维白化以消除信号的相关性，最后使用Fast-ICA算法分离Walsh码软扩频多址信号，估计用户数目以及每位用户的伪码序列。仿真实验和分析表明，在一定信噪比范围内，算法能实现Walsh码软扩频多址信号盲分离且分离不多于5条(8，3)Walsh码软扩频信号。