基于模糊逻辑和机动检测的AGIMM跟踪算法

邵 堃, 雷迎科

(国防科技大学电子对抗学院, 合肥,230037)

随着信号处理技术研究的日益深入和成熟，目标跟踪在导弹防御、战场监视、港口避碰、交通管制、车辆导航和机器视觉等许多军事和民用领域都扮演着重要的角色，而目标模型的选择又是上述技术中不可或缺的重要组成部分。目前卡尔曼滤波算法、扩展卡尔曼滤波(Extended Kalman Filter，EKF)算法和无迹卡尔曼滤波(Unsented Kalman Filter，UKF)算法等经典的跟踪算法[1-2]只适用于单一数学模型描述的目标机动形式，在实际应用中，由于目标具有多阶段机动特性且机动参数很难获得，因此传统的单模型算法很难完整地描述目标的机动特性。为了解决该问题，Blom和Bar-Shalom[3]提出了一种具有Markov切换系数的交互式多模型(Interacting Multiple Model，IMM)算法，并在目标跟踪领域得到了广泛应用和发展[4-10]。

但是IMM算法的跟踪性能在很大程度上依赖所选取的模型集[11-12]，为了提高算法的跟踪精度，就要使模型尽可能地覆盖目标运动的全过程，但较多的模型不但会增加计算量而且可能产生模型竞争使算法跟踪效果下降。为了解决这个问题，变结构交互多模型算法(Variable Structure Interacting Multiple Model，VSIMM)[13-17]被提出，文献[18]提出的基于协同转弯(Coordinate Turn，CT)模型的自适应网格交互多模型(Adaptive Grid Interacting Multiple Model，AGIMM)算法是VSIMM 算法的一种，AGIMM算法克服了传统IMM算法运用协同转弯模型(Coordinate Turn,CT)[19]时必须知道真实转弯率这一难点，因此AGIMM算法可以用较少的运动模型完成对机动形式复杂目标的有效跟踪，目前以协同转弯模型为基础模型集的AGIMM算法[20]已经发展成为最有效的跟踪算法之一。

但目前AGIMM系列算法仍存在下列问题：一是AGIMM算法在其网格结构调整时过多地依赖上一时刻的网格模型，导致在目标不进行机动的阶段算法的模型集收敛较慢；二是目前机动检测的方式非常依赖模型的后验概率和单个模型的残差信息[21]。由于目标机动、存在观测误差和模型不准确等原因，目标的真实运动模式不总出现在最接近最大模型概率对应的模型处，因此容易产生错误的机动检测结果。本文针对上述存在的问题提出基于模糊逻辑和机动检测的AGIMM(AGIMM Tracking Algorithm Based on Fuzzy Logic and Maneuvering Detection，FLMD-AGIMM)跟踪算法，首先通过模糊逻辑算法自适应地得到机动检测可信度，然后利用机动检测可信度信息、目标的机动信息和模型后验概率信息重新给出网格结构调整方式，提高模型的收敛速度。仿真表明，改进的算法相对于AGIMM算法加快了模型集的收敛速度，提高了目标跟踪精度。

1 协同转弯跟踪模型

X(k+1)=FX(k)+GW(k)

(1)

式中：

2 AGIMM 算法

ωC(k+1)=μL(k)ωL(k)+μC(k)ωC(k)+

μR(k)ωR(k)

(2)

每次循环后算法中模型的角速度都会得到更新，左边模型和右边模型是在中间模型的基础上根据模型的后验概率、最小网格间距以及探测阈值来更新的，具体的AGIMM算法网络调整方式见文献[20]。

3 FLMD-AGIMM算法

由于AGIMM算法对模型进行调整时过分依赖前一时刻的网格结构，导致模型集收敛速度较慢。本文提出的FLMD-AGIMM算法是通过模糊逻辑算法自适应地将机动检测信息引入AGIMM算法的模型调整过程中，即利用机动检测可信度信息、模型后验概率和目标的机动信息重新给出模型的网格结构调整方法。

3.1 基于模糊逻辑的机动检测

传统的机动检测方法是根据预测的残差信息对目标是否机动进行检测，因为残差作为滤波算法中的后验信息充分反映了目标当前时刻的状态变化。AGIMM算法中有3个子模型，k时刻滤波得到的残差分别为v1(k)、v2(k)和v3(k)，求k时刻最大后验概率max(μk)对应的残差的范数。

(3)

式中：S(k)为残差的协方差。

S(k)=H(k)P(k|k-1)HT(k)+R(k)

(4)

Dj(k)服从量测维数值的χ2分布，根据χ2分布性质，设置门限值M，若Dj(k)>M，则目标发生机动，反之目标不发生机动。目标发生机动的典型概率值取0.01时，M=7；目标发生机动的典型概率值取0.1时，M=3。

但上述机动检测方法非常依赖模型的后验概率和单个模型的残差信息。当目标运动状态改变和存在误差时，每次滤波得到的最大模型概率对应的模型并不总是最接近目标真实运动模式的模型，若根据最大后验概率对应模型的残差信息进行机动检测容易产生错误的结果，因此引入模糊逻辑理论对机动检测可信度进行计算，在模型的网格结构调整过程中加入机动检测可信度信息。

模糊逻辑算法[23-24]的基本思想是通过原始的逻辑语言形式，通过一组模糊规则模拟人的经验和逻辑，在提出的FLMD-AGIMM算法中采用模糊控制器的目的是计算单模型残差信息的机动检测可信度，首先确定模糊输入变量：最大后验概率μmax(k)和模型网络间距Δω，Δω计算方式见式(5)：

(5)

μmax(k)属于模糊集{小，中，大}；Δω属于模糊集{很小，小，中，大}，由大量实验积累的经验得到各输入变量对应的隶属度函数如图1所示。

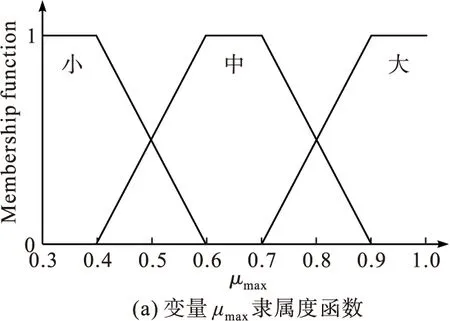
图1 输入变量的隶属度函数

FLMD-AGIMM算法中包含3个模型，最大后验概率μmax(k)对应的是该时刻最接近目标真实运动状态的模型，当存在观测误差、模型不准确和模型竞争等情况时，该对应方式可能出现偏差。Δω表示FLMD-AGIMM算法3个模型的离散程度，即网格大小，若Δω很小时，3个网络模型参数很接近，此时3个模型的残差信息相差不大，因此利用最大后验概率对应的模型的残差信息进行机动检测结果是可信的。根据经验制定模糊规则，模糊控制器的推理过程可以采用Takagi-Sugeno (TS)模型具体表述为：

Ifμmax(k)is A anddis B, thenP(k) is C，

k=1,2,…,l

根据输入输出变量的含义以及经验知识可得到如下结论: 若最大后验概率μmax(k)很小且模型网络间距Δω很大，则根据最大后验概率μmax(k)对应模型的残差信息得到的机动判决结果可信度很小，P(k)可以视为0，以此类推可得到其他模糊逻辑规则，具体见表1，输出变量对应的隶属度见图2。在对模糊控制器的输出进行解模糊化时，采用中位数法进行解模糊化，得到机动检测的具体可信度。

当模糊匹配输出的机动检测可信度P(k)为[0，0.4)时不进行机动检测；当输出概率为(0.4，0.6]可能进行机动检测；当输出概率为(0.6，1]进行机动检测。

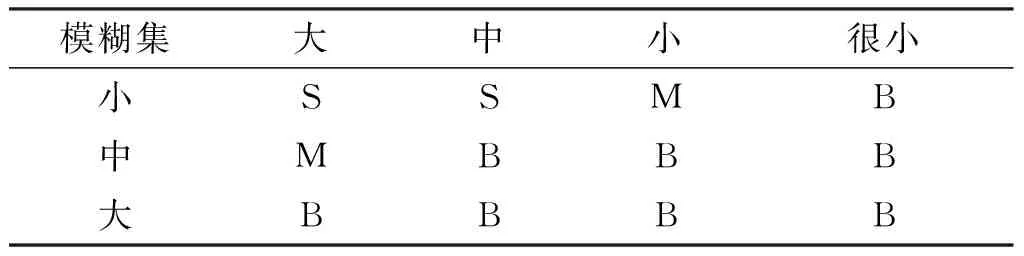
表1 系统模糊逻辑规则

图2 输出变量的隶属度函数

3.2 网格模型调整

首先设定一个阈值T，若P(k)≤T，说明机动检测信息的可信度较低，此时根据后验概率μ(k)在原网格模型的基础上调整网格中心。

ωC(k+1)=μL(k)ωL(k)+μC(k)·

ωC(k)+μR(k)ωR(k)

(6)

根据后验概率、设定模型探测阈值t1、t2和最小网格间距δ1调整左边模型和右边模型，其中t1∈[0,1]、t2∈[0,1]。

1)当max(μk)=μC(k)时:

(7)

(8)

式中：λ1=max{ωC(k)-ωL(k),δ1}；λ2=max{ωR(k)-

ωC(k),δ1}；t1取一个很小的值。

2)当max(μk)=μL(k)时:

(9)

式中:t2取一个较大的值。

ωR(k+1)=ωC(k+1)+λ2

(10)

3)当max(μk)=μR(k)时:

(11)

ωL(k+1)=ωC(k+1)-λ2

(12)

若P(k)>T，说明机动检测信息的可信度较高，此时将机动检测信息加入模型调整过程，加快模型收敛速度。

1)当μmax(k)=μC(k)时，即最大概率是中心模型。

若DC(k)>M，则认定目标进行了机动。根据后验概率μ(k)在原网格模型的基础上调整网格中心。

ωC(k+1)=μL(k)ωL(k)+μC(k)ωC(k)+

μR(k)ωR(k)

(13)

在调整左右两边的模型时加入目标的机动信息，若模型残差值大，则说明目标进行了较强的机动，则增加网格探测范围，反之减小网格探测范围。

(14)

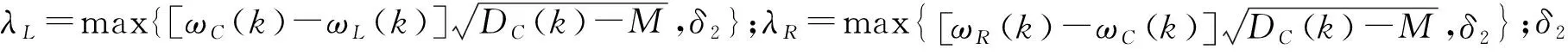
若DC(k)≤M，则认定目标不发生机动，证明目标的运动较稳定，所以此时充分相信后验概率μ(k)，加快模型集的收敛速度。

ωC(k+1)=ωC(k)

(15)

在调整左右两边的模型时，依据各自模型对应的后验概率值的大小，在原有网格间距的基础上，若左边模型概率小则减小左边探测区域，反之增加网格探测区域。

ωL(k+1)=ωC(k+1)-γL[1-μR(k)]

(16)

若右边模型概率小则减小网格右边探测区域，反之增加网格探测区域。

ωR(k+1)=ωC(k+1)+γR[1-μL(k)]

(17)

式中：γL=max{ωC(k)-ωL(k),δ3}；γR=max{ωR(k)-ωC(k),δ3}，δ3为最小网格间隔。

2)μmax(k)=μL(k)时，即最大概率是左边模型。

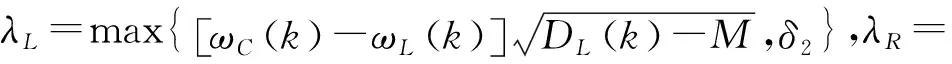
若DL(k)≤M，则认定目标不发生机动。根据后验概率重新调整模型中心点:

ωC(k+1)=ωL(k)

(18)

在调整左边的模型时，在原有网格间距的基础上，若左边模型后验概率大则增加左边探测区域，反之减小网格探测区域。

ωL(k+1)=ωC(k+1)-γL[1-μR(k)]

(19)

右边模型网格间距如式(20)所示：

ωR(k+1)=ωC(k+1)+γR

(20)

3)当μmax(k)=μR(k)时，即最大概率是右边模型。

若DR(k)≤M，则认定目标不发生机动。根据后验概率重新调整模型中心点:

ωC(k+1)=ωR(k)

(21)

左边模型网格间距为：

ωL(k+1)=ωC(k+1)-γL

(22)

计算右边模型时，在原有网格间距的基础上，若右边模型后验概率大则增加右边探测区域，反之减小网格探测区域。

ωR(k+1)=ωC(k+1)+γR[1-μL(k)]

(23)

4 仿真实验及结果分析

系统的量测方程可以建立在目标与观测站径向距离r、目标相对观测站的俯仰角β、方位角α可以测量的基础上。

Z(k+1)=H[X(k+1)，k+1]+V(k+1)

(24)

式中：H[X(k+1)，k+1]=[r(k+1)α(k+1)β(k+1)]T。

(25)

式中：V(k+1)为量测噪声，其协方差矩阵为：

(26)

4.1 目标运动轨迹

4.1.1 轨迹1

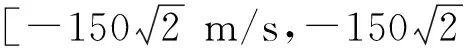
图3 目标运动轨迹1

4.1.2 轨迹2

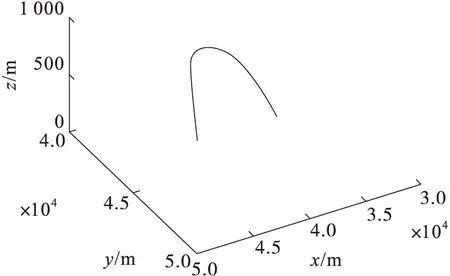
图4 目标运动轨迹2

4.1.3 轨迹3

为验证算法对高速运动目标的跟踪性能，以文献[20]中的X-51A导弹轨迹为例，目标的初始位置为[600 km,30 km,1 km]，初始速度[-1 800 m/s,0 m/s,0 m/s]，第1阶段t=0～20 s，目标做直线运动，x轴方向机动加速度为0 m/s2，y轴方向机动加速度为9.8 m/s2；第2阶段t=21～380 s，目标做匀速转弯运动，角速度为5.6°/s；第3阶段t=381～400 s目标在x方向机动加速度为0，y方向机动加速度为-9.8 m/s2。

4.2 算法性能对比

用目标状态估计值的均方根误差(Root Mean Square Error, RMSE)[25]为性能指标来衡量本文提出算法的性能。

(26)

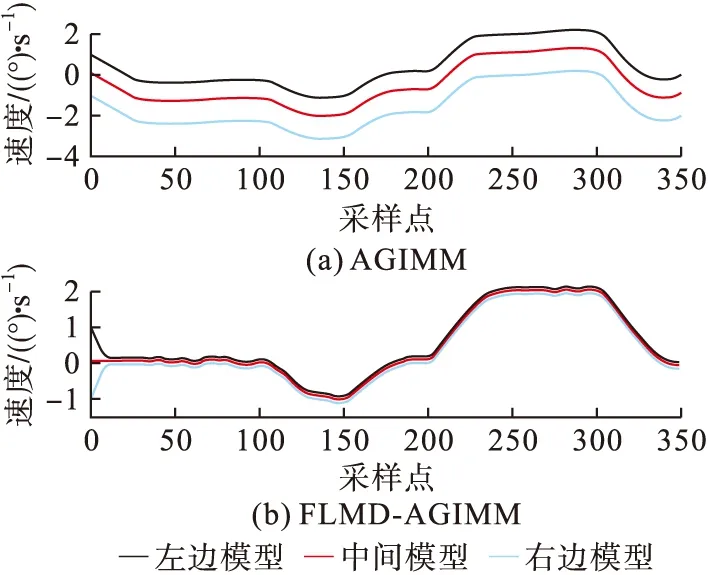
图5 模型角速度变化对比

图5仿真结果表明，FLMD-AGIMM算法模型角速度的收敛速度明显快于AGIMM算法，当目标运动状态稳定时，FLMD-AGIMM算法可以快速调整模型网格中心点，并且根据模型后验概率使左边模型和右边模型迅速收敛。

2)仿真2：分别将轨迹1、轨迹2和轨迹3作为实验的目标运动轨迹，比较IMM算法和AGIMM算法和FLMD-AGIMM算法的跟踪性能，其中IMM算法包括匀速直线运动(Constant Velocity, CV)模型、匀加速运动(Constant Acceleration, CA)模型和CT模型。实验量测噪声的标准差为σr=100 m，σα=σβ=0.2°，对目标2跟踪时采样间隔为0.5 s，对目标1和目标3采样间隔为1 s，其余实验参数同实验1。仿真结果见图6～8。

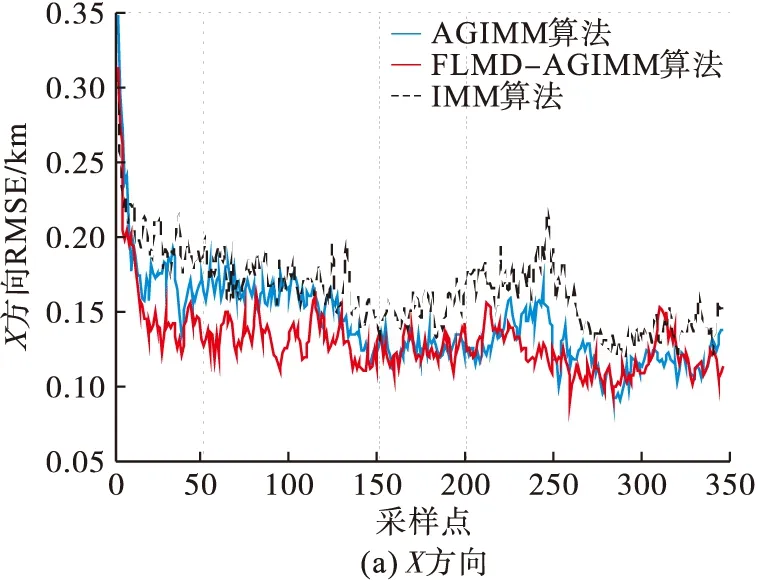
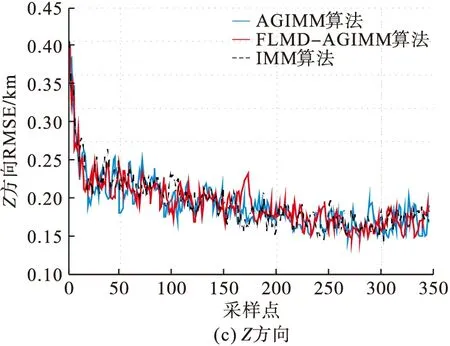
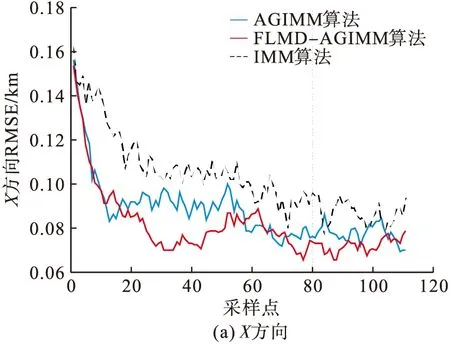
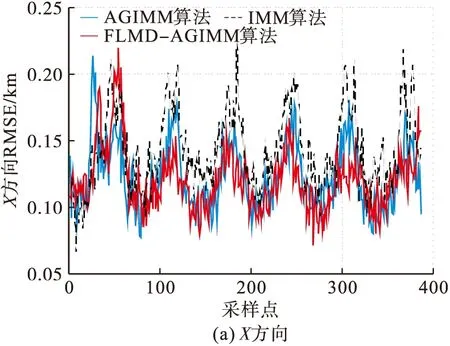
如图所示，当目标在机动状态发生改变时，IMM算法由于其模型参数固定导致算法跟踪精度变低，如图6中的第120个采样点附近、第180个采样点附近，图7中第40个采样点附近。而AGIMM算法和FLMD-AGIMM算法的网络结构可以自适应地改变，因此能保持较好的跟踪精度，但由于AGIMM算法的网络模型调节效率较慢限制了其跟踪精度。由图6～8可以看出，无论是对目标1、目标2还是目标3进行跟踪，FLMD-AGIMM算法的跟踪性能都优于IMM算法和AGIMM算法。

3)仿真3：选择轨迹1作为实验的目标运动轨迹，在不同量测条件下，比较IMM算法和AGIMM算法和FLMD-AGIMM算法的跟踪性能，条件如表2所示，其他参数同实验2，结果如表3所示。

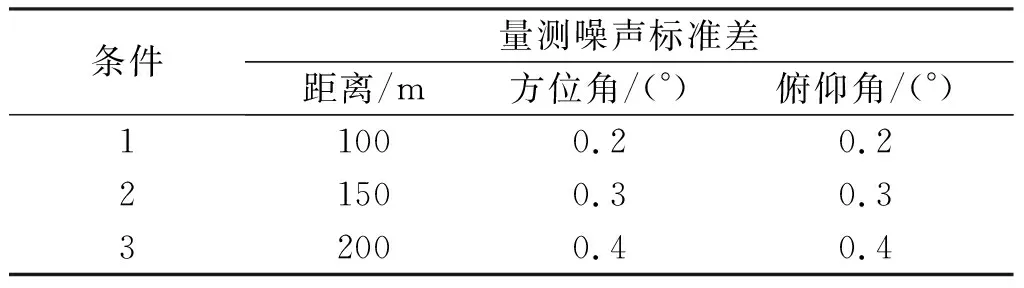
表2 量测噪声标准差

表3 3种算法的平均位置RMSE比较

4)仿真4：选择轨迹1作为实验的目标运动轨迹，在不同初始模型条件下，比较FLMD-AGIMM算法和AGIMM算法的跟踪性能，初始模型集参数如表4所示，量测噪声的标准差为σr=100 m，σα=σβ=0.2°，其他条件与仿真1相同。

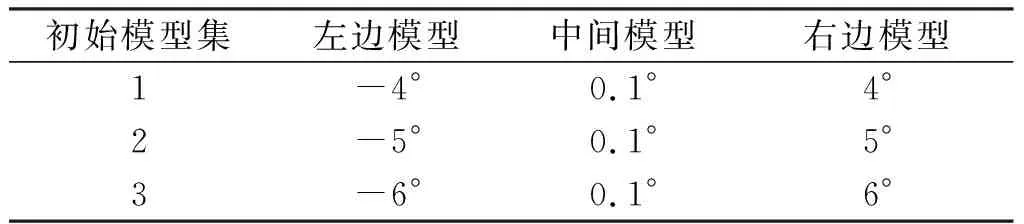
表4 不同初始模型集参数

由表5结果可以看出随着初始模型集的网格间距变大AGIMM算法的跟踪性能随之降低，而FLMD-AGIMM算法的跟踪性能仍能保持在较好的水平，这得益于FLMD-AGIMM算法中改进的模型网格调整方式，当目标在非机动情况下模型集可以快速与真实目标运动模式匹配，使算法可以较少地受初始模型集的影响。

表5 2种算法在不同模型集下的平均位置RMSE比较

5 结语

针对AGIMM算法网格模型收敛速度慢和机动检测方法过于依赖单个模型后验概率的问题，本文提出了FLMD-AGIMM算法。该算法首先通过模糊逻辑算法对单模型机动检测可信度进行检测，然后利用机动检测可信度信息调整网络结构，克服了机动检测方法受观测误差、模型竞争和模型不准确等因素的影响；当机动检测可信时通过目标的机动信息和模型的后验概率重新给出了在机动检测时模型网格的调整方法，解决了AGIMM算法网格模型收敛速度慢的问题。仿真结果表明，相对于AGIMM算法，本文所提出的算法具有更快的模型收敛速度和更高的目标跟踪精度。