基于多重测量矢量的含旋转部件目标ISAR成像方法

张 群, 蒋国建, 康 乐, 李开明

(空军工程大学信息与导航学院，西安，710077)

在逆合成孔径雷达(Inverse Synthetic Aperture Radar，ISAR)成像中[1]，为简化处理，一般假设目标为刚体目标，此时目标上所有散射点都具有相同的运动参数。然而在实际成像时，目标往往不满足刚体模型，目标中部分散射点的运动状态较为复杂，存在机械振动、旋转运动等运动形式，对雷达回波信号产生频率调制，这种调制称之为“微多普勒(Micro-Doppler)效应”[2-4]。微多普勒效应广泛存在于实际目标中，如螺旋桨飞机、直升机、弹道导弹、大型舰船等。当采用传统的距离-多普勒(Range-Doppler，R-D)算法对此类目标进行成像时，微多普勒效应会对目标主体信号产生干扰，表现为在ISAR图像中附加的干扰条带，降低了目标的ISAR图像质量。解决这一问题，主要有两种思路，一是从目标回波中剔除旋转部件信号以实现对目标主体成像，二是通过分离目标主体和旋转部件的信号，分别进行成像处理。基于前一种思路，文献[5]利用Chirplet分解剔除了活动部件的成像干扰分量，并对成像图进行轮廓特征提取。但是，这类方法注重微动信号的分离和抑制，仅能获得目标主体部分的ISAR图像，损失了目标旋转部件的信息。而基于后一种思路，文献[6]利用Hough变换在谱图域分离了目标主体信号和旋转部件信号，实现了具有大旋翼的空中目标ISAR成像；文献[7]在双基地ISAR系统中对含旋转部件目标进行了研究，提出了一种修正的扩展Hough方法，成功分离了目标的微多普勒信号。然而，文献[6～7]均属于图像域处理的方法，当微动散射点较多时，在距离慢时间像中剔除微动信号会导致主体信号的严重缺损，从而影响成像质量。由于这一问题在图像域处理难以避免，因此需要考虑基于信号域处理的旋转部件信号分离方法。

压缩感知(Compressed Sensing, CS)理论是由数学家Donoho于2006年提出的一种新的信号获取与处理理论[8]。2007年，Baraniuk等人首次将CS理论应用到雷达成像中，证明了压缩感知雷达成像的可行性[9]。CS理论中的基本模型就是从单重测量信号中恢复未知的稀疏信号，称之为单重测量矢量(SMV)模型。多重测量矢量(MMV)模型是在SMV模型的基础上被提出的，即从多重测量信号中恢复具有相同稀疏结构的未知稀疏信号。目前基于MMV模型的重建算法主要有凸优化算法、贪婪算法和基于时序结构的稀疏贝叶斯算法三类[10]。文献[11]对MMV模型在ISAR成像中的应用进行了研究，将ISAR成像过程中的所有一维距离像作为一个整体，而后将ISAR成像问题转化为MMV模型的稀疏重构问题并对其优化求解。

本文主要将MMV模型应用到含旋转部件目标ISAR成像中。首先建立了含旋转部件目标的ISAR成像转台模型，分别对目标主体信号和旋转部件信号的多普勒进行分析，得出目标主体信号在方位向的稀疏性和旋转部件信号在方位向的非稀疏性；而后建立目标主体信号的线性模型，找到目标主体信号在方位向的固定支撑集。通过低维观测信号与恢复矩阵，利用MMV-OMP算法即可获得目标主体信号的成像结果。在此基础上，从回波信号分离得到旋转部件信号，并利用逆Radon变换对其进行成像。

本文组织结构如下：第1节简单介绍了压缩感知基本理论与MMV模型，第2节建立了含旋转部件目标信号模型，第3节提出了含旋转部件目标ISAR成像方法,第4节通过仿真实验来验证本文方法的有效性，最后一节是结论。

1 压缩感知基本理论与MMV模型

假设一个未知的N维信号x可以被线性表示，即：x=Ψs，Ψ为基矩阵。如果系数向量s中存在k(k≪N)个非零元素，则称s为信号x在基矩阵Ψ上的k稀疏表示。

如果利用低维观测矩阵Φ对信号x进行观测，则得到M维的观测信号y，可以表示为：

y=Φx=ΦΨs=Acss

(1)

其中Acs=ΦΨ。对于上式的求解，如果Acs满足约束等距特性(Restricted Isometry Property, RIP)，可将其转化为最小l1范数凸优化问题[12]：

min‖s‖1, s.ty=Acss

(2)

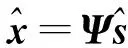
(3)

对于M个N维信号x来说，如果每个信号的稀疏结构相同，那么可以利用观测矩阵Φ对M个信号同时进行观测，得到M个观测结果，即：

Y=ΦX

(4)

式中：X=[x1,x2,…,xM]，Y=[y1,y2,…,yM]。这种利用信号稀疏结构特性的CS观测模型称为多重测量矢量(MMV)模型[13]。

2 含旋转部件目标信号模型

假设目标的平动补偿已经完成，则ISAR成像模型可以用转台模型表示，如图1所示。图中O点为目标成像中心，成像投影平面由坐标系XOY构成，雷达到目标成像中心的距离为Rref。在成像时间内，主体散射点P的坐标为(x,y)，以角速度ω匀速转动，到成像中心的距离为Rp，初相为θ0。坐标系UO′V中，旋转散射点Q以角速度ωQ绕O′作半径为rQ的匀速圆周运动，初相为θQ。

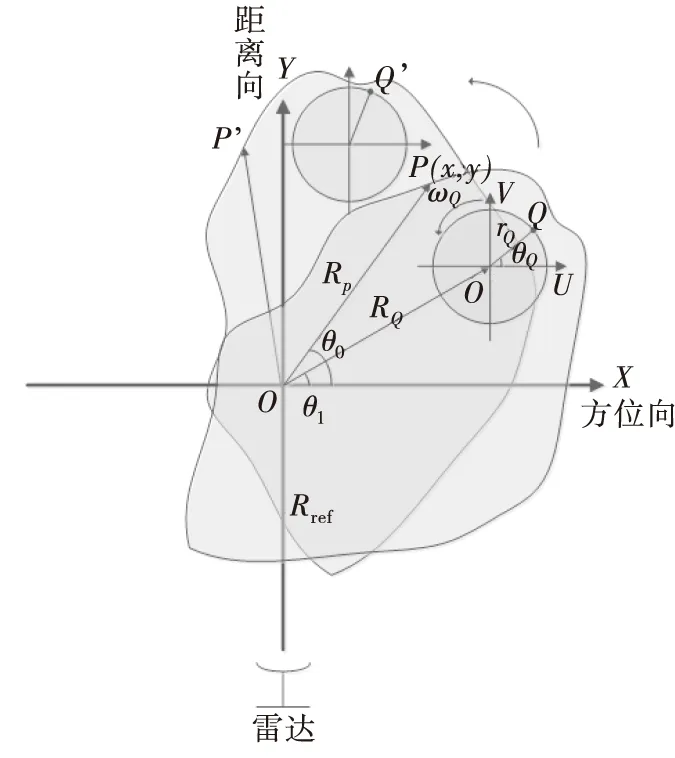
图1 含旋转部件目标转台模型

雷达发射线性调频信号：

(5)

(6)

式中：σPi、σQk分别为第i个主体散射点和第k个旋转散射点的散射系数；c为光速；λ=c/fc为波长；RΔi(tm)=Ri-Rref，RΔk(tm)=Rk-Rref，Ri、Rk分别表示主体散射点与旋转散射点到雷达的距离。

对式(6)进行距离压缩后，得到距离压缩信号为：

(7)

式中：B为带宽。

由图1可得，主体散射点P对应的RΔP为：

RΔP(tm)=RPsin(ωtm+θ0)

(8)

在小角度观测条件下，sinωtm≈ωtm，cosωtm≈1，则P点的多普勒为：

(9)

而对于旋转散射点Q，其对应的RΔQ为：

RΔQ(tm)=RQsin(ωtm+θ1)+rQsin(ωQtm+θQ)

(10)

同理可以推出Q点的多普勒为：

(11)

由式(9)、(11)可得主体散射点的多普勒为恒定值，因此对目标主体信号在方位向做傅里叶变换就可以实现方位向聚焦。而旋转散射点的多普勒附加了一个正弦调频信号，直接在方位向做傅里叶变换将导致散焦，产生宽度与旋转半径为正比的干扰条带。

3 含旋转部件目标ISAR成像方法

3.1 目标主体回波分离与成像

在小角度观测条件下，RΔP(tm)≈xωtm+y，由此可将目标主体的基频回波信号重新表示为[14]：

(12)

式中：σ(x,y)表示目标主体的散射系数。

(13)

将式(13)代入式(12)得到目标主体的ISAR观测信号离散模型为：

(14)

式中：n=0,1,…,N-1；m=0,1,…,M-1；l=0,1,…,L-1；h=0,1,…,H-1。上式可以表示为：

S1=FσΦ

(15)

对主体回波信号S1进行距离压缩，可将主体回波距离压缩信号Sr1表示为：

Sr1=S1Φ-1=Fσ

(16)

此时将目标回波距离压缩信号重新表示为：

Sr=Sr1+Sr2=Fσ+Sr2

(17)

式中：Sr2为旋转散射点的回波信号S2进行距离压缩后得到的信号，具体表示为：

(18)

在ISAR成像中，单个脉冲信号进行距离压缩后可以得到目标强散射点在距离向上的信息，对于多个脉冲信号形成的回波矩阵来说，距离压缩以后就可以得到目标的距离-慢时间谱图，在目标不越距离单元徙动时，则对于目标主体散射点来说，目标主体散射中心回波距离压缩后的能量聚集于固定的某个距离单元内，多个脉冲中包含的距离向信息相同，其距离-慢时间谱图由直线谱构成。因此可以将MMV模型应用到ISAR成像中，如图2所示。

图2 MMV模型

在CS理论中，Acs需满足RIP性质，文献[15]已证明当观测矩阵Φ和基矩阵Ψ不相干时，Acs高概率满足RIP性质。本文选择广义单位阵Φ=[φk,m]作为观测矩阵，其中(k=1,2,…,K;m=1,2,…,M)。满足与傅里叶基F不相干。在Φ中的任意行向量Φk中，随机选取一个元素为1，其他元素均为0。对距离压缩后的回波信号Sr进行观测得到：

(19)

在得到观测结果后，可由恢复矩阵Acs通过求解凸优化问题来求解。由于取得的支撑集中只包含有目标主体回波的信息，因此利用此恢复矩阵求解的解中不包含有旋转部件回波的信息，从而剔除旋转部件对目标主体信号的干扰。本文利用MMV-OMP重构算法对信号进行求解，具体流程如表1所示。

表1 多重观测矢量模型-正交匹配追踪算法

3.2 基于逆Radon变换的旋转部件成像

在得到目标主体ISAR像以后，就可以利用其主体散射点分布来生成主体回波信号，从而在回波信号中减去主体回波信号，即可得到旋转部件回波信号，对旋转部件回波信号利用逆Radon变换进行成像。

由式(7)可得旋转散射点Q的距离压缩回波信号为：

(20)

将式(10)代入上式，并在小角度观测条件下进行化简得散射点Q的距离压缩回波信号包络为：

mag{sQ(r,tm)}=σQB·

(21)

由上式可得旋转散射点Q在距离-慢时间的谱图为一条以RQsinθ1为中心的正弦曲线，幅度为rQ，周期与旋转散射点Q相同。

逆Radon变换可以实现正弦曲线到参数空间的映射[16]。将旋转散射点Q的距离-慢时间包络写为如下形式：

f(r,θ)=δ(r-rQsin(θ+θQ))

(22)

其逆Radon变换后图像为：

g(x,y)=

drdkxdky=δ(x-rQsinθQ)δ(y-rQcosθQ)

(23)

式中：kx=vcosθ，ky=vsinθ。因此，利用逆Radon变换就可以实现旋转散射点在成像平面的重建。

4 仿真分析

4.1 点目标仿真实验

首先进行点目标仿真实验。仿真参数设置如下：雷达载频fc为10 GHz，带宽B为600 MHz，发射线性调频信号，脉冲宽度Tp为10-6s，PRF为256 Hz，目标运动速度为300 m/s。假设目标由5个非旋转散射点和2个旋转散射点组成，如图3(a)所示。其中2个旋转点(图中用“*”标出)的初始坐标分别为(3 m,0 m)和(0 m,3 m)，旋转中心为成像中心，旋转半径为3 m，旋转频率为12 Hz。

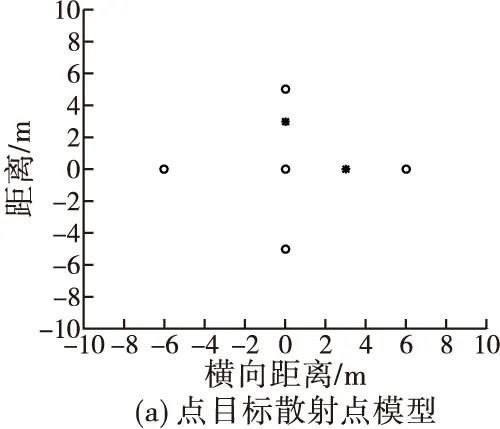
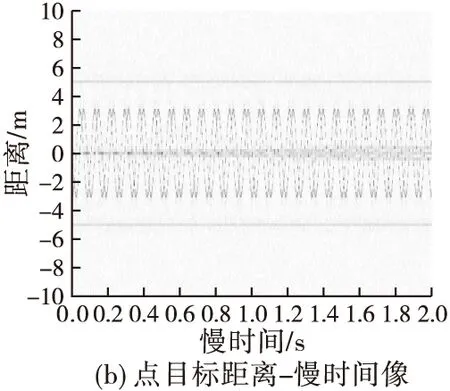
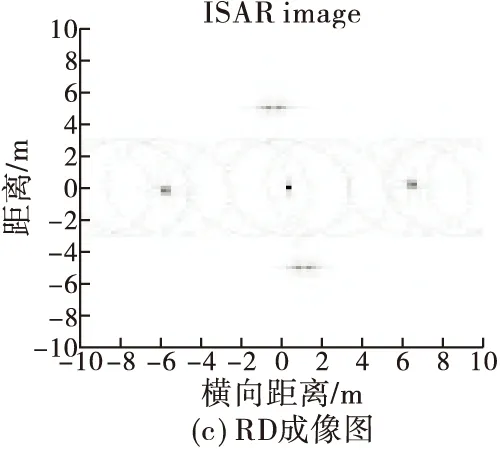
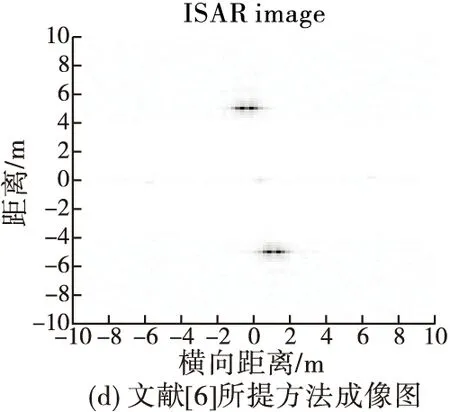
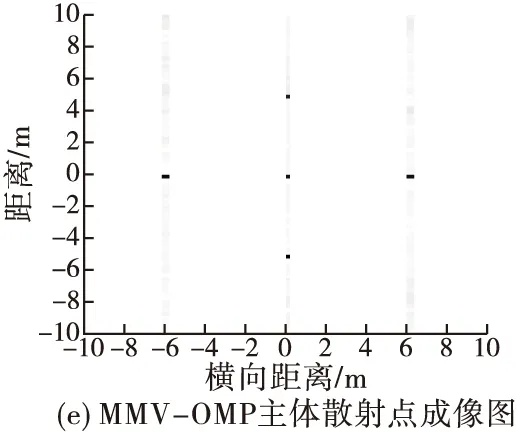
图3 点目标仿真结果

在回波信号中加入了高斯白噪声，信噪比SNR为-13 dB。图3(b)是点目标的距离-慢时间像，从图中可以看出目标的距离-慢时间像由非旋转散射点的直线谱和旋转散射点的正弦曲线谱构成。对回波信号利用传统的距离多普勒(RD)算法直接成像，得到的结果如图3(c)所示：由于旋转散射点的存在，ISAR图像中附加了沿多普勒方向的调制干扰带，成像结果受到了污染。图3(d)是利用文献[6]所提图像域处理方法成像结果，由于旋转散射点旋转频率较高，由图3(b)可以看出旋转散射点的正弦曲线谱较为密集，而利用文献[6]所提方法不仅仅会去掉距离慢时间谱图中的正弦曲线谱，也会使旋转散射点谱图和主体散射点谱图相交处均置0，从而导致主体信号严重缺损，从图中可以看出，处于旋转散射点覆盖距离单元内的3个主体散射点成像效果较差。图3(e)是利用本文所提方法成像结果，可以看出得到的目标主体像已基本消除了旋转散射点的影响，对比图像域处理方法也不会丢失主体散射点的信息，ISAR图像的质量得到了提高。图3(f)为利用逆Radon变换对旋转散射点回波进行成像结果。为进一步比较RD成像图与本文所提方法成像图的成像质量，分别计算点目标原图(不包含2个旋转散射点)、文献[6]所提方法成像图、RD成像图、和本文所提方法成像图的图像熵，如表2所示，可以看出RD成像图的图像熵值和文献[6]所提方法成像图的图像熵值相比原图熵值较大，本文所提方法成像图的图像熵值较低，聚焦效果较好，同时相比其他两种成像方法成像图更接近原图图像熵值，成像质量较高。

表2 图像熵值比较

4.2 直升机模型仿真实验

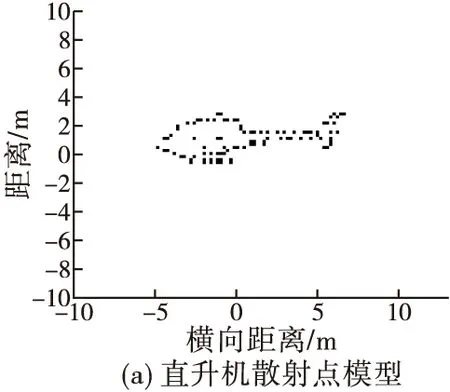
为进一步验证本文所提方法的有效性，采用64个散射点构成的直升机仿真模型进行仿真实验。仿真参数设置如下：雷达载频fc为10 GHz，带宽B为600 MHz，发射线性调频信号，脉冲宽度Tp为10-6s,PRF为300 Hz，目标运动速度为100 m/s。设置3个旋转散射点模拟直升机水平旋翼的旋转，旋转半径均为2 m，旋转频率为6.566 7 Hz。

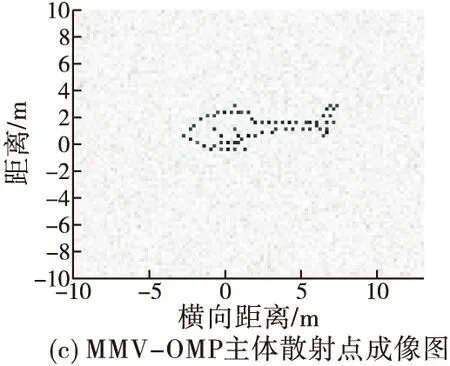
在回波信号中加入了信噪比SNR为-13 dB的高斯白噪声，图4(a)为直升机散射点模型。首先对回波信号利用传统的距离多普勒(RD)算法直接成像，得到的结果如图4(b)所示。由于旋转部件产生的微多普勒效应，对ISAR主体像产生了污染，成像效果不佳。而后利用本文所提方法首先对ISAR主体部分进行成像，由图4(c)可以看出，目标的固定散射点基本被重构出来，成像效果较佳。图4(d)为利用逆Radon变换对旋转散射点回波进行成像的结果，通过此图像可以得到3个旋转散射点相对旋转中心的初始位置。

在回波信号中分别加入信噪比SNR为-8 dB，-13 dB，-18 dB的高斯白噪声，同时使用本文所提方法和文献[6]所提方法分别进行成像，得到的成像结果如图5、6所示。利用成像结果和原图计算均方误差(MSE)来衡量图像重建质量，结果如表3所示。通过对比本文所提方法在不同信噪比下的成像结果和MSE可以发现，随着SNR的降低，图像重建误差逐渐增大，成像质量逐渐下降。这是由于噪声的增大，干扰了距离压缩信号和恢复矩阵的相关性，使得成像质量下降。同时比较同一信噪比下不同成像算法的成像结果和MSE可以发现，利用本文方法所得ISAR像重建误差均小于文献[6]所提方法得到的ISAR像重建误差，因此本文所提方法的成像效果优于文献[6]所提方法。

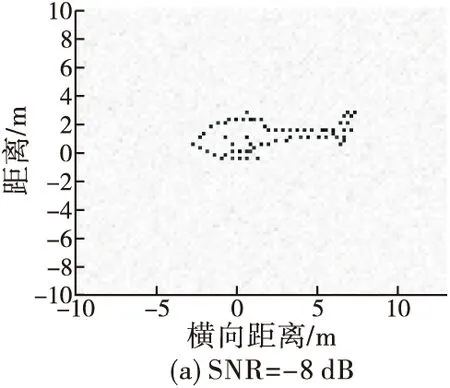
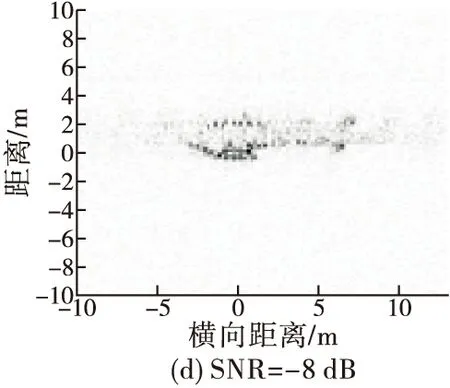
表3 不同信噪比下图像重建误差

综上所述，本文所提方法可以在信噪比较高的条件下利用含旋转部件目标的回波信号分别得到目标主体的ISAR像和旋转部件的ISAR像，避免了图像域处理方法中主体回波信息丢失的缺陷，有效提高了目标主体的ISAR像质量。

5 结语

本文针对含旋转部件目标的ISAR成像问题，提出了一种基于多重测量矢量的含旋转部件目标ISAR成像新方法，利用主体信号和旋转部件信号在方位向的稀疏性差异，通过寻找主体信号在方位向的固定支撑集，对距离压缩信号进行重构求解，得到了目标主体的ISAR像。而后利用目标主体像来生成主体回波信号，以此得到旋转部件回波信号，并利用逆Radon变换对旋转部件进行成像。仿真实验验证了该方法的有效性。