星-弹双基SAR建模及成像特性分析

郭 苹, 焦晓阳, 王安义, 王 静

(西安科技大学通信与信息工程学院，西安，710054)

随着低成本火箭发射技术、微小卫星平台技术和载荷技术的迅猛发展，实现全球信息，特别是天基信息共享的“天地一体化”体系正在全世界范围内引发广泛研究[1]。双基地合成孔径雷达(BiSAR)将收发站放置在2个不同平台上，结合了双基雷达和SAR的特点，具有隐蔽性强、抗干扰、信息获取丰富、可前视成像等诸多优点[2-5]。与传统的BiSAR[6-9]不同，SMB-BiSAR的接收机安装在距离战场较近的导弹上，而发射机位于距离战场较远的空间卫星上，将卫星平台独特的空间特性与导弹的机动灵活优势相结合，使得弹载SAR可以有效获取包含背景在内的目标景象进行图像匹配处理，实现精确定位、制导等功能，提高打击能力。另外，导弹作为接收端无需发射大功率信号其被检测概率大大降低，从而增强了系统的抗干扰、抗侦察能力[10]。在“天地一体化”体系的背景下，研究SMB-BiSAR成像很有意义。然而SMB-BiSAR的优势是以结构复杂性为代价的，卫星如何协助导弹成像将成为新的挑战。

在SAR成像研究中，成像机理、成像性能以及信号特性，可从理论上反映场景目标的成像可能性和分辨能力，且与后期成像算法的研究和系统参数的设计密切相关[10-11]。关于传统BiSAR，例如机载BiSAR，星载BiSAR的研究起步较早，成像处理技术也相对比较成熟。在传统的BiSAR系统中，飞行平台通常要求做匀速直线飞行。无论对于发射平台还是接收平台，经典的双曲线模型假设都可以很好地直接应用[5-6]。由于不同平台结合带来的优势，近年来，关于混合BiSAR，例如星-机级联SAR的成像特性及成像算法的研究也逐渐增多[12-13]。但是，考虑到收发平台的复杂几何结构及飞行特性，对于曲线飞行的卫星、飞机及导弹平台而言，直接应用经典的双曲线模型将会带来较大的相位误差，在文献[14]和[15]中提出了利用切比雪夫多项展开式代替泰勒级数展开式的方法提高距离模型的精度。在文献[8]中对星-机双基地SAR的空间几何关系及信号模型进行了研究。孙稚超等人对地球同步轨道星-机双基SAR的性能以及构型设计进行分析，明确了在空间分辨率和成像信噪比约束下机载接收站的路径规划[12]。文献[16]从模糊函数的角度，推导了通用双基SAR的分辨率表达式。然而，与机载SAR相比，导弹运动存在较大空间三维速度和加速度，尤其在末端俯冲下降段，以导弹作为接收机的成像几何构型会更加复杂[17-18]，但目前关于SMB-BiSAR这一双基构型的研究较少。只有文献[19]进行了简单的研究。

本文针对SMB-BiSAR这一特殊成像体制，分别在地心固定坐标系和参考点本地坐标系中，构建空间几何模型，对收发平台的成像模型进行矢量描述，得到目标的距离历程以及回波信号模型。然后，利用距离等值线与多普勒等值线的正交关系，对接收站的飞行路径约束条件进行分析。最后，根据距离分辨率与多普勒分辨率及两者梯度的关系，得到SMB-BiSAR距离和方位分辨率的计算公式，并进行仿真验证。

1 空间几何关系及信号模型

考虑卫星轨道差异、导弹机动飞行等复杂情形，相比于常规单、双基模式，星/弹SAR几何模型发生较大的变化，首先在地心固定坐标系中对SMB-BiSAR的空间几何进行分析，得到卫星的位置矢量和运动矢量，然后选取在更适合成像处理的参考点本地坐标系中建立信号模型进行特性分析。图1为SMB-BiSAR空间几何关系。

图1 SMB-BiSAR空间几何关系

由于在地心固定坐标系中进行距离历程和回波相位的分析比较复杂，所以我们建立了参考点本地坐标系，如图1(b)所示。在参考点本地坐标系中，波束中心点P0变为坐标原点，Z轴由地心指向参考点方向。

利用坐标系转换，首先将地心固定坐标系绕Z轴逆时针旋转θa，然后再绕Y轴顺时针旋转π/2-θe，最后沿Z轴将坐标系平移地球半径长度Re，得到以波束中心为坐标原点的参考点本地坐标系。在该坐标系中，卫星的位置矢量Rt0和运动矢量(Vt,At)可以分别表示为：

(1)

式中：旋转矩阵M0和M1分别可以表示为：

(2)

(3)

在合成孔径时间内，卫星和导弹分别沿轨迹lt和lr运动。Pt是任意点目标P的位置矢量。点E和点F分别为参考时刻(η=0)发射站和接收站的位置。在任意方位η时刻，发射站和接收站的位置矢量分别为Rt(η)和Rr(η)，即:

(4)

式中：Rr0为接收站即导弹的初始位置矢量；Vr和Ar分别是导弹的速度矢量和加速度矢量。从物理学运动的角度出发，斜距模型是对雷达平台与观测目标之间相对运动的准确描述，因此，斜距建模是开展后续信号模型、多普勒参数分析、图像几何分辨率评估和成像方法等研究的必要条件。基于上述分析，在参考点本地坐标系中，任意点目标P的距离历程可以表示为:

r(η)=|RT(η)|+|RR(η)|=

|Rt(η)-Pt|+|Rr(η)-Pt|

(5)

式中:|·|为取模操作符。

假设发射信号是线性调频信号(LFM)，则目标的回波信号可以表示为：

(6)

式中：t为快时间；c为光速；λ为波长；ωr(·)和ωa(·)分别是距离和方位窗函数。

根据文献[20]可知，利用泰勒级数展开对距离历程进行矢量分析，其物理含义更明确，为了便于特性分析，将式(5)在η=η0时刻进行泰勒级数展开：

(7)

式中：κn是展开系数，κn(Pt)=μn(Rr0,Pt)+μn(Rt0,Pt)，则展开式可表示为：

(8)

式中：R是距离矢量。当R代表发射站距离矢量时，V和A指的是η0时刻发射站的运动参数；当R代表接收站距离矢量时，V和A表示为η0时刻接收站的运动参数。

如图2所示，式(7)带来的相位误差的最大值远小于π/4，这表示对距离模型采取三阶泰勒级数近似带来的相位误差对最终成像质量造成的影响可以忽略。

图2 三阶泰勒级数展开相位误差

2 飞行路径约束分析

在SMB-BiSAR系统中，卫星的运行轨道固定，但导弹的运动方式相对比较灵活，从而保证了系统的灵活性。作为SMB-BiSAR系统成像指标中重要参数之一，空间分辨率与收发平台的相对位置、运动状态都息息相关。文献[9]中通过将无人机路径规划问题建模为多目标优化问题，获得最适合的无人机路径实现GEO-UAV星机双基SAR成像任务。因此，为了保证在待成像区域获得高分辨的二维成像，导弹的飞行路径显然也必须满足一定的约束条件以获得更好的空间分辨率。这里我们从双基几何构型的角度对导弹的飞行路径约束条件进行简单的分析。由于距离等值线和多普勒等值线在成像场景中的分隔特性可以反映在不同区域的成像能力，我们首先对距离等值线与多普勒等值线进行分析。在方位η时刻，场景中双站距离和为Rη的距离等值线与多普勒频率和为fdη的多普勒等值线可以表示为:

(9)

如果希望在待成像区域获得高分辨的二维成像，要遵循的直观构型设计原则是使得距离等值线与多普勒等值线正交或准正交[2]。由于梯度方向即距离等值线和多普勒等值线的法向量方向，所以我们首先分析两者梯度的正交性。距离梯度和多普勒梯度可以表示为：

Rη=[|RT(η)|+|RR(η)|]=

UT(η)+UR(η)=U∑(η)

(10)

(11)

(12)

(13)

式中：0≤Ω≤π/2，可以利用式(13)设计BiSAR的几何构型。当探测区域的Ω接近90°时，聚焦结果较好，反之聚焦性能降低。与单基SAR相比，BiSAR具有更为灵活的设计优势，通过合理选择系统几何构型，使探测区域的Ω接近90°，获得更好的等距线与等多普勒线的正交性。因此，可以根据Ω对导弹的飞行路径进行简单的约束限制。

3 空间分辨率分析

分辨率特性是BiSAR系统的重要理论基础，该体制雷达的核心就是要获取目标的高分辨率图像。由于SMB-BiSAR与传统的BiSAR模式不同，我们有必要对该新构型的距离和方位分辨率的计算公式进行新的推导。根据文献[21]和[22]可知，距离分辨率与多普勒分辨率与两者梯度有关，则距离分辨率可以表示为：

(14)

式中：Br是发射信号带宽。将式(10)代入到式(14)可得：

(15)

式中：β是UT和UR之间的双基地角。距离分辨率反映了2个点目标在距离方向上的分辨能力。当Br一定，ρr与双基地角β有关。由于卫星和导弹的相对运动，在整个成像场景中的双基地角是变化的，因此距离分辨率随目标位置而变化。

SAR的方位分辨率是衡量多普勒频率差异的能力。因此，多普勒频率差对于方位分辨率的推导是重要的。由于方位分辨率与多普勒频率的梯度有关[17]，可以表示为：

(16)

式中：Ta为合成孔径时间。将式(11)代入式(16)，方位分辨率可表示为：

(17)

根据半角公式，可以得到：

|UT(Ta/2)-UT(-Ta/2)|=2sin(θT/2)≈θT

(18)

|UR(Ta/2)-UR(-Ta/2)|=2sin(θR/2)≈θR

(19)

式中：θT和θR分别是发射站和接收站的方位合成角或者相干积累角，分别与发射站和接收站的方位分辨率有关，则方位分辨率可表示为：

(20)

式中：eT和eR分别是发射站和接收站在方位方向上的单位矢量；α为eT和eR夹角。可以看出，方位分辨率由发射站和接收站的分辨率以及发射站和接收站的运动方向共同决定，我们可以通过设置合理的导弹运动方向，得到高分辨的SMB-BiSAR构型。

4 仿真分析

在SMB-BiSAR系统中，如果正确规划了接收站的运动路径，则可以构造多种成像模式。除了采用这种新型双基地构型的传统宽带成像模式外，还可以实现前视和大斜视模式成像。这里首先对本文中飞行路径约束的分析进行验证，然后对SMB-BiSAR的前视分辨能力进行仿真，参考点本地坐标系中的收发平台的参数信息由表1给出。

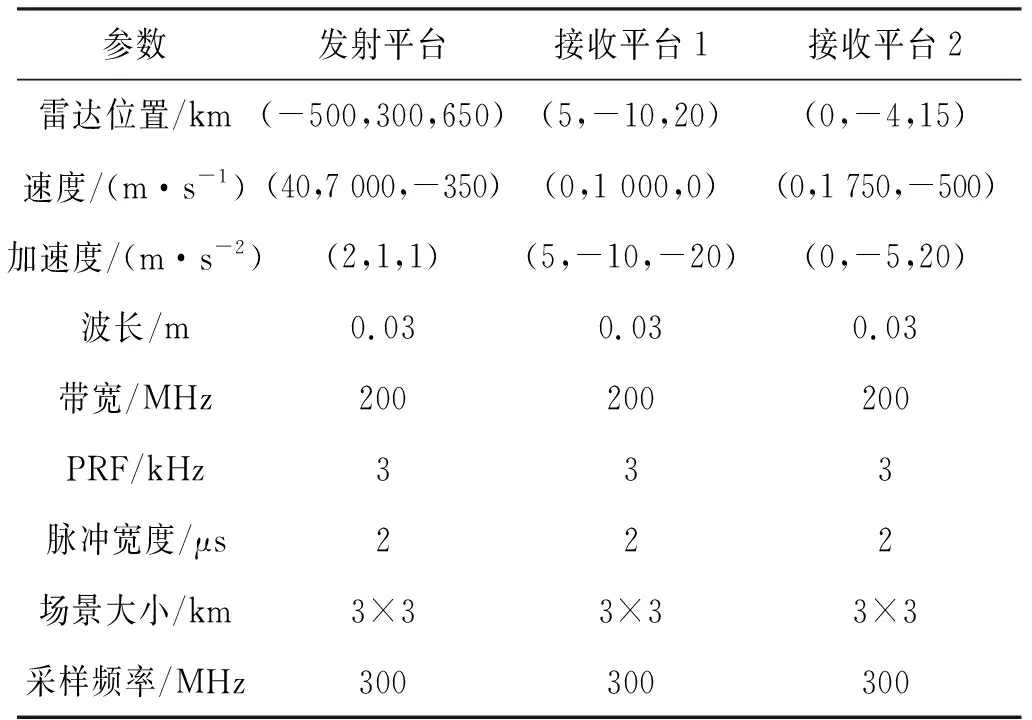
表1 仿真参数收发平台参数信息

图3表示利用表1中的参数进行仿真得到的SMB-BiSAR等距离/等多普勒线示意图，图中紫色五角星表示接收站，场景中心点位于坐标原点(0,0)位置。红色虚线和黑色实线分别是距离等值线和多普勒等值线。在图3(a)中可以看到，绿色条带状区域的距离等值线与多普勒等值线夹角Ω都相对较小，甚至接近零，这意味着该区域的距离方位耦合严重，对于回波数据的处理较难。而位于接收站大前斜方向的椭圆区域中，红色和黑色线条构成的矩形或近似矩形区域表示距离等值线和多普勒等值线正交或者近似正交，这说明通过调整接收站的位置，SMB-BiSAR可以实现对成像区域的大前斜视成像。同理，由图3(b)中可以看到，绿色条带状区域的距离等值线与多普勒等值线夹角Ω都相对较大，甚至接近180°，同样说明该区域的距离方位耦合严重，难以实现二维成像处理。而位于接收站正前方的椭圆区域中，距离等值线和多普勒等值线正交或者近似正交，这说明SMB-BiSAR在前视模式下具有二维成像分辨率的能力。

图3 SMB-BiSAR等距离等多普勒线

为了验证分辨率分析的正确性，利用表1中接收站1的参数，对距离分辨率和方位分辨率的计算进行仿真。由于距离分辨率与传统双基模式计算方法相同，这里只对距离分辨率与目标位置及双基夹角的变化关系进行分析，如图4所示。

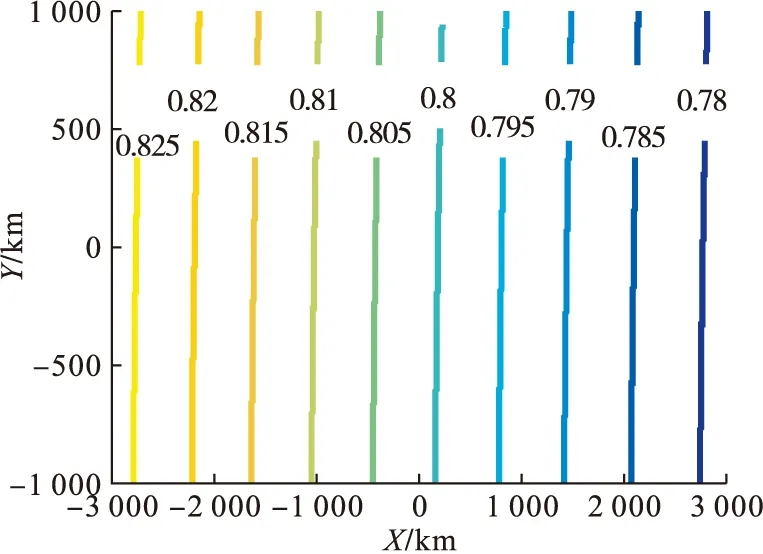
图4 SMB-BiSAR距离分辨率

距离分辨率随目标位置而变化，沿距离向变化大而沿方位向的变化小；另外，当发射站和接收站之间的夹角β越大时，距离分辨的效果越差，而当夹角β=0时，收发站位置重合，变为单基情况，距离分辨率效果最佳。

图5给出了方位分辨率的计算结果，并利用后向投影算法(Back Projection Algorithm, BPA)聚焦结果进行对比。如图5(a)所示,利用式(17)计算得到场景中心点目标(0,0)的分辨率数值为1.312 m，而根据3 dB波束宽度计算得到的方位分辨率理论值为1.311 m，如图5(b)所示。通过对比可知，利用本文推导方法计算得到方位分辨率误差为0.076%，满足误差要求。

图5 SMB-BiSAR方位分辨率

图6给出了方位分辨率随接收站和双基角的变化示意图，Y轴表示单基情况下导弹的方位分辨率，X轴表示夹角α。给定接收站的方位分辨率，当α小于某一数值时，SMB-BiSAR可以实现优于单基情况的分辨率。

例如，假设单基情况下导弹的方位分辨率为0.5 m，当α小于120°时，SMB-BiSAR的方位分辨率优于单基情况的导弹方位分辨率。当单基方位分辨率大于1 m时，大部分情况SMB-BiSAR的方位分辨率是更优于单基导弹的方位分辨率。另外，由单基情况下导弹的方位分辨率ρα=1.14 m的方位分辨率图可知，发射站和接收站运动方向的夹角越大，方位分辨率越差。当α=0时，发射站和接收站运动方向相同，方位分辨率效果最佳。

5 结语

SMB-BiSAR作为一种特殊的成像模型，将卫星平台独特的空间特性与导弹的机动灵活优势相结合，可以实现对目标区域的精确定位、制导等功能。本文针对SMB-BiSAR这一特殊成像体制，分别在地心固定坐标系和参考点本地坐标系中，构建空间几何模型，对收发平台的成像模型进行矢量描述，得到目标的距离历程以及回波信号模型。然后，利用距离等值线与多普勒等值线的正交关系，对接收站的飞行路径约束条件进行分析，根据距离分辨率与多普勒分辨率与两者梯度的关系，得到SMB-BiSAR距离和方位分辨率的计算公式。最后，通过仿真实验对SMB-BiSAR的大前斜和前视成像能力进行验证。仿真结果验证了本文分析方法的有效性。