基于优化的卷积神经网络的蛋白质二级结构预测

赵亚武 刘毅慧

(齐鲁工业大学(山东省科学院)计算机科学与技术学院 山东 济南 250353)

0 引 言

蛋白质是生命活动的物质基础，是构成细胞的基本有机物，是生命活动的主要承担者。蛋白质的结构决定了它的功能，因此对蛋白质结构的预测，具有非常大的研究价值。在生物信息学领域，很难从初级结构预测出蛋白质的空间结构，因此蛋白质二级结构[1]预测研究受到很多人的重视。

目前，有很多根据蛋白质的初级结构预测其二级结构的基本方法。近年来，大数据、深度学习等技术应用十分广泛，结合深度学习模型预测蛋白质的二级结构成为研究的一种趋势。张蕾等[2]融合了基于递归神经网络和前馈神经网络的深度学习模型来预测8类蛋白质二级结构。Wang等[3]利用支持向量机(SVM)的策略在CB513数据集上得到了76.11%的Q3准确率，但是该模型只适用于小数据集，在大数据集上精度难以提高。Liu等[4]在ASTRAL数据集上利用小波提取PSSM矩阵特征并结合卷积神经网络，在三折交叉验证后，得到76.9%的Q3准确率。Patel等[5]提出了神经网络预测蛋白质二级结构方法，在RS126和CB396数据集测试中，Q3的精度分别达到了90%和82%。Spencer等[6]组合特定位置打分矩阵信息和深度学习网络架构,得到的预测准确率为80.7%。Ma等[7]提出了GTPC方法，测试在CASP9和CASP10数据集上正确率为83.92%和83.07%。Ma等[8]还提出一种基于数据分割和半随机子空间方法，在25PDB和CB513数据集上测试3态准确率为86.38%和84.53%。文献[9]融合卷积神经网络和长短时记忆神经网络模型，应用到蛋白质8类二级结构预测中。

上述模型大都是对深度网络结构的改进，靠增加特征来提高预测精度，但对网络模型参数的选择基本是手工调节，这些模型的参数并没有达到最优化。为了解决这一问题，本文融合贝叶斯优化和卷积神经网络模型用于蛋白质二级结构的预测。首先对数据集进行处理，将数据分成训练集、验证集和测试集三个部分，并构建初始的卷积神经网络模型；然后将卷积神经网络的层数、学习率、梯度冲量和正则化系数四种超参数配合训练集和验证集构建贝叶斯优化算法，通过训练网络，不断优化得到最优的网络参数；最后通过测试集数据得到准确率。实验结果表明，本文所提出的模型能够取得较好的效果。

1 蛋白质二级结构预测模型

蛋白质3类二级结构预测问题是在给定蛋白质序列的基础上来预测每一个氨基酸残基所对应的二级结构类型，氨基酸残基之间的相互作用决定了蛋白质序列二级结构。因此本文采用贝叶斯优化卷积神经网络的模型提取氨基酸之间的局部作用和位置信息进行蛋白质二级结构预测。

1.1 模型结构

为了确定最佳的卷积神经网络结构，本文选择使用贝叶斯优化的方法优化相关参数。首先对数据进行处理，选取PSSM矩阵的前20列,采用滑动窗口的方式对PSSM矩阵处理，在滑动窗口为13时，在蛋白质序列前后补上6个0，依次对蛋白质序列从前往后选取数据，得到大小为20×13的二维PSSM矩阵，其次，将PSSM矩阵作为卷积神经网络的输入。本文模型结构如图1所示。

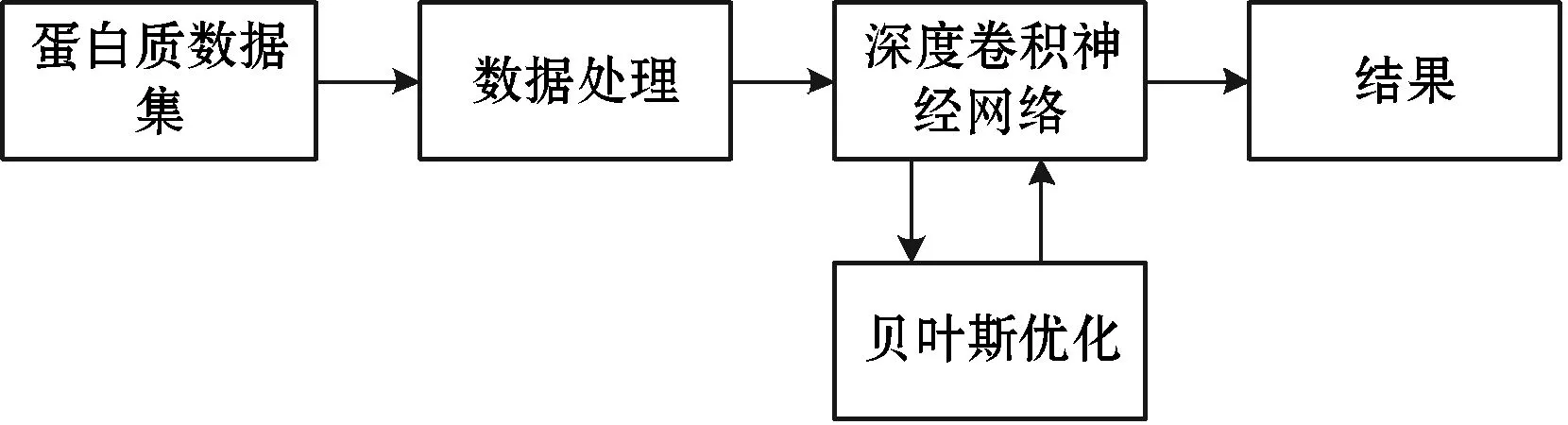
图1 模型结构图

1.2 蛋白质数据集

ASTRAL数据集[10]是2013年发布的版本scope2.03，共包含59 514条蛋白质，包含蛋白质数据库中65%以上的蛋白质结构。本文所用到的ASTRAL数据集有6 892条蛋白质，序列同一性低于25%，CullPDB[11]数据集含有12 288条蛋白质。将ASTRAL和CullPDB作为训练集，去除ASTRAL和CullPDB数据集中的重复蛋白质后，一共有15 696条蛋白质。

本文从CASP数据集[12-14]中收集了几个用于测试网络的数据集，CASP9中包含68条蛋白质,CASP10中包含有51条蛋白质,CASP11中包含36条蛋白质,CASP12中含有9条蛋白质，CASP数据集中的蛋白质在训练集中去除。CB513数据集[14]和25PDB数据集[15]也用于评估本文模型，CB513数据集包含513条蛋白质序列，任何两种蛋白质彼此的序列同源性均小于25%。25PDB数据集的低序列相似性不超过25%，有1 672条蛋白质。除去与训练集相同的蛋白质序列，CB513和25PDB剩余411条和999条蛋白质用于测试。本文用CASP11数据集作为验证集。

基于PSI-BLAST的位置特异性评分矩阵(PSSM)含有丰富的生物进化信息[16]，可以对蛋白质库中的蛋白质序列进行比对并打分，得到相对完整的蛋白质残基序列信息，能够改善蛋白质二级结构的预测精度。本文采用的PSSM进化矩阵是在nr数据库上进行多序列比对且PSI-BLAST参数设置为阈值是0.001和3次迭代得到的PSSM矩阵是20×N矩阵，其中N是氨基酸序列的长度，20是氨基酸类型的数目，因此PSSM矩阵对蛋白质序列中的每一个残基都有20个特征。文献[2]和文献[6]都将PSSM矩阵作为特征矩阵输入来预测蛋白质二级结构。在广泛使用的蛋白质结构定义DSSP中包含有8种二级结构[17]，分别为H(α螺旋)、B(β转角)、E(折叠)、G(3-螺旋)、I(5-螺旋)、T(转角)、S(卷曲)和L(环)。

本文实验将G、H、I替换为H，B、E替换为E，其他都采用C的划分方式。

1.3 卷积神经网络模型

近年来，卷积神经网络作为流行的深度学习算法，它的结构主要包含输入层、隐含层和输出层。隐含层又包含了多个卷积层和池化层，通过卷积层和池化层特征提取，通过输出层进行分类。伴随着深度学习理论的提出和计算速度的提高，卷积神经网络得到了快速发展，被广泛应用于计算机视觉[18]、图像分割[19]和自然语言处理[20]等方面，卷积神经网络基本框架如图2所示。

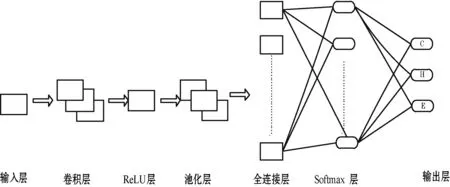
图2 卷积神经网络结构

图2中卷积层、ReLU层以及池化层能够充分学习数据特征，防止过拟合，提高模型的泛化能力。

1.3.1卷积层

卷积层是通过卷积核对输入的数据利用局部连接和权值共享进行局部特征提取。卷积层每个神经元的输入来自上一层特征图的特定区域的神经元，这个特定区域的大小由卷积核来决定。卷积的过程就是卷积核按照一定的步长在输入矩阵的感受野上做卷积运算，并产生和卷积核个数相等的特征图。每一个区域都要通过输入矩阵和权重相乘，然后再加上偏置参数b，可以得到特征图。令：

(1)

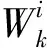
(2)

式中：bk为偏置参数;f为激活函数，激活函数选取ReLU函数。

激活函数的作用是对卷积层输出做非线性操作，使得网络模型的表达能力，选用ReLU函数作为激活函数。

1.3.2池化层

池化方法作为卷积神经网络的超参数，主要包括最大池化和平均池化两种。最大池化层并不执行任何的学习，它通常也被称为一种非线性的下采样形式。最大池化处理的结果是使特征维度下降、参数减少来减少计算量，提高计算速度，并且还能有效地减少过拟合，同时还有平移不变的特性，增加了鲁棒性。通过设置池化层来划分特征图的区域，在每个区域进行最大池化运算来输出区域的最大值。平均池化和最大池化的区别在于平均池化是对区域内的点求平均。

1.3.3全连接层和Softmax层

全连接层每个神经元都要和前面一层的神经元连接起来，并且全连接层的神经元之间互不连接，从而可以把卷积层和池化层提取到的局部特征综合起来，得到全局特征。

Softmax层就是输出层，输出层是由三个神经元组成，该层的输出满足：

(3)

式中：j为类别，对应蛋白质的H、E、G，使用Softmax函数输出3类蛋白质二级结构的概率Pj(j=1,2,3)。

1.4 贝叶斯优化

近年来，伴随着计算机科学技术的发展，催生了各个行业和领域的兴起，这些行业产生的较大的数据量也需要用到较为复杂的决策算法。针对以上复杂的问题，贝叶斯优化(Bayesian optimization, BO)是一种有效的解决方法[21]。伴随着蛋白质序列的不断增多，将卷积神经网络模型应用到蛋白质二级结构预测中，调节卷积神经网络的超参数需要花费很长时间，因此本文使用了贝叶斯优化算法优化卷积神经网络的超参数。贝叶斯优化算法只需要经过几次目标函数评估就可以获得较好的结果，并且贝叶斯优化算法已经广泛应用于游戏[22]、推荐系统[23]和导航[24]等领域。

本文所提出的模型指定了卷积神经网络的架构和要优化的变量。要优化的变量包括学习率、梯度冲量、正则化系数和网络层数，把这些变量作为训练算法的选项。使用训练数据和验证数据作为输入为贝叶斯优化器创建目标函数，该函数把将要优化的变量作为输入来训练、验证网络，并保存网络用于测试集上。

对于卷积神经网络超参数的优化可以看作对未知的黑盒函数的优化，贝叶斯优化是在有界的集合D上找到损失函数f(x)最小值，它可以为函数f(x)构造概率模型并利用该模型判断集合D怎么去评估函数。首先假设高斯核函数为被优化的黑盒函数，再选择一个采集函数来确定下一个采样点。超参数的贝叶斯优化是超参数对损失函数f(x)进行高斯先验建模：

(4)

由于在验证集上观测是带有噪声的，所以给每一个观测值加上一个高斯噪声，即：

f(x)=L(mx,Vh)+θ

(5)

1.4.1优化超参数

在使用高斯过程回归时，不需要声明具体的函数形式。任意有限个超参数引起了多变量的高斯分布，由协方差函数K和均值函数μX所决定。即：

L～GP(μX,K)

(6)

式中：K*=[k(x*,x1),k(x*,x2),…,k(x*,xn)]T，x*代表超参数。

假设输入超参数Xi=(x1,x2,…,xn)在验证集上得到输出Y=L(xi,Vh)(i=1,2，…，n)，在每一次实验中，高斯函数根据超参数X和验证集输出Y来评估f(x)，然后再通过采集函数选择下一组超参数。超参数Xi的预测分布表示为：

(7)

式中：f(xi)表示超参数的预测分布；K表示协方差函数。

1.4.2采集函数

在贝叶斯优化卷积神经网络参数的过程之中，在每一次迭代过程中，用来采样下一组超参数，采集函数观察f(x)，再对下一次采样的超参数进行比较，在最大程度上找到最优解。Expected Improvement(EI)[26]定义如下：

a(x|D)=E[max(0,fx-fbest)]

(8)

式中：fbest是基于验证集最优解。EI使用标准的black-box优化算法进行优化。

在最优提取函数条件下，贝叶斯优化算法在理论上一定可以收敛[21]，目标函数在迭代过程中会选择最优的样本点进行评估，在保证迭代次数的前提下，算法一定可以收敛到最优。贝叶斯优化注重于减少评估的代价，可以大大减少优化的时间，在经过几次目标函数的评估就可以得到卷积神经网络的最优参数和网络结构。

2 实验与结果分析

本文实验环境如下：采用MATLAB R2018b软件运行模型程序，集群硬件由4台NF5280M5、1台NF5288M5、两台千兆交换机组成，NF5280M5配置tesla V100 GPU(16 GB显存)计算卡，NF5288M5配置tesla V100 GPU(32 GB显存)计算卡，集群所有节点安装Centos7.4 X64标准系统。

通过贝叶斯优化卷积神经网络的超参数，可以发现网络层数、学习率、梯度冲量和正则化系数对测试集的准确率有一定影响，调节超参数过程如表1和表2所示(网络层数包括：输入层、卷积层、ReLU层、池化层、全连接层和Softmax层)。

表1 13窗口超参数

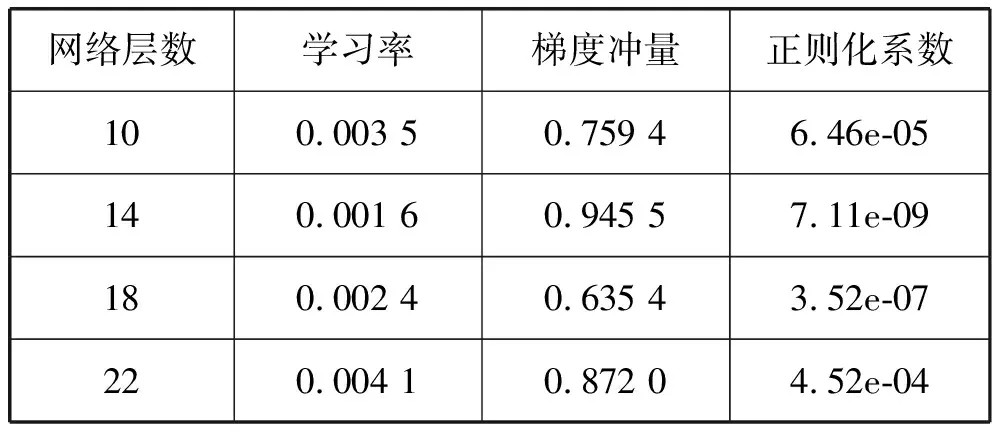
表2 19窗口超参数

通过调节超参数可以得到不同的预测正确率，和最好准确率下的网络模型结构，如表3和表4所示。

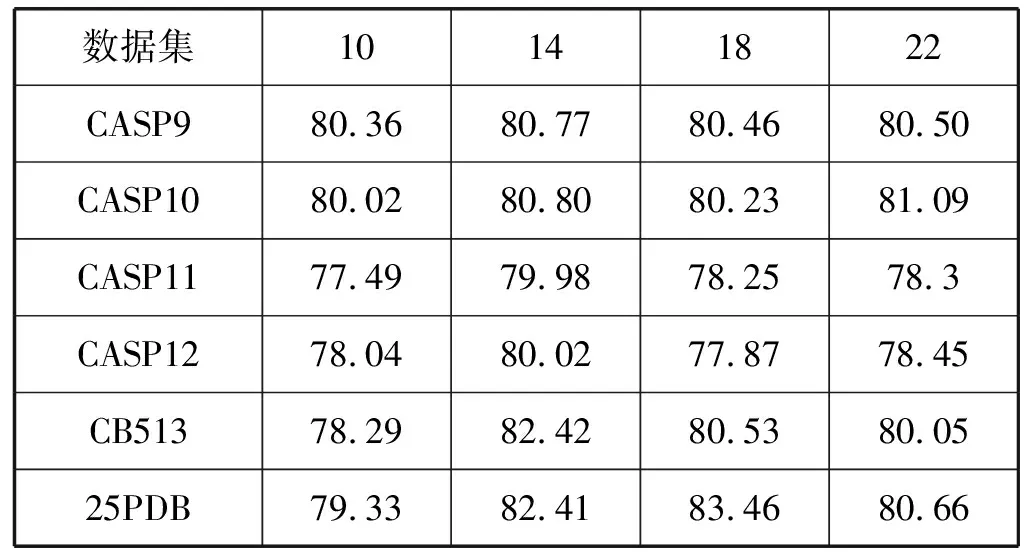
表3 13窗口准确率

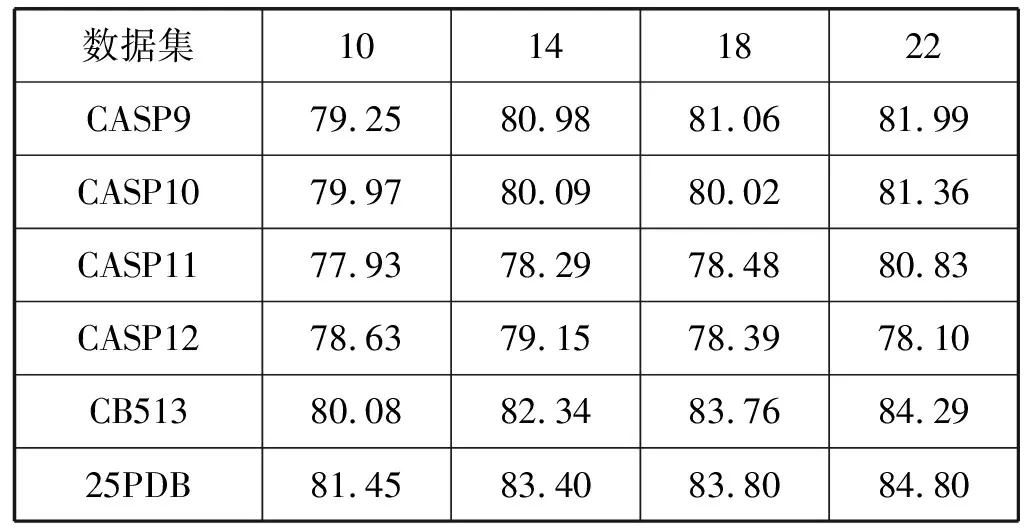
表4 19窗口准确率

池化方法也是卷积神经网络的超参数，表3和表4所示的准确率所采用的池化方法为最大池化，为了得到最佳网络超参数，将平均池化方法和最大池化方法进行对比。平均池化方法的准确率如表5和表6所示。

表6 19窗口下平均池化准确率

通过表3、表4和表5、表6对比可以得到最优的网络结构模型，滑动窗口为13时，网络模型结构为：4个卷积层，前两个卷积层卷积核大小11，个数91，后两个卷积层卷积核大小2，个数182，每一个卷积层后都加上ReLU层并且每隔两个卷积层后有一个池化大小为2,步长为2的最大池化层。滑动窗口为19时，网络模型结构为8个卷积层，前四个卷积层卷积核大小19，个数64，后四个卷积层卷积核大小8，个数128，每一个卷积层后都加上ReLU层并且每隔四个卷积层后有一个池化大小为2步长为2的最大池化层。在滑动窗口为19时，网络模型结构如表7所示。

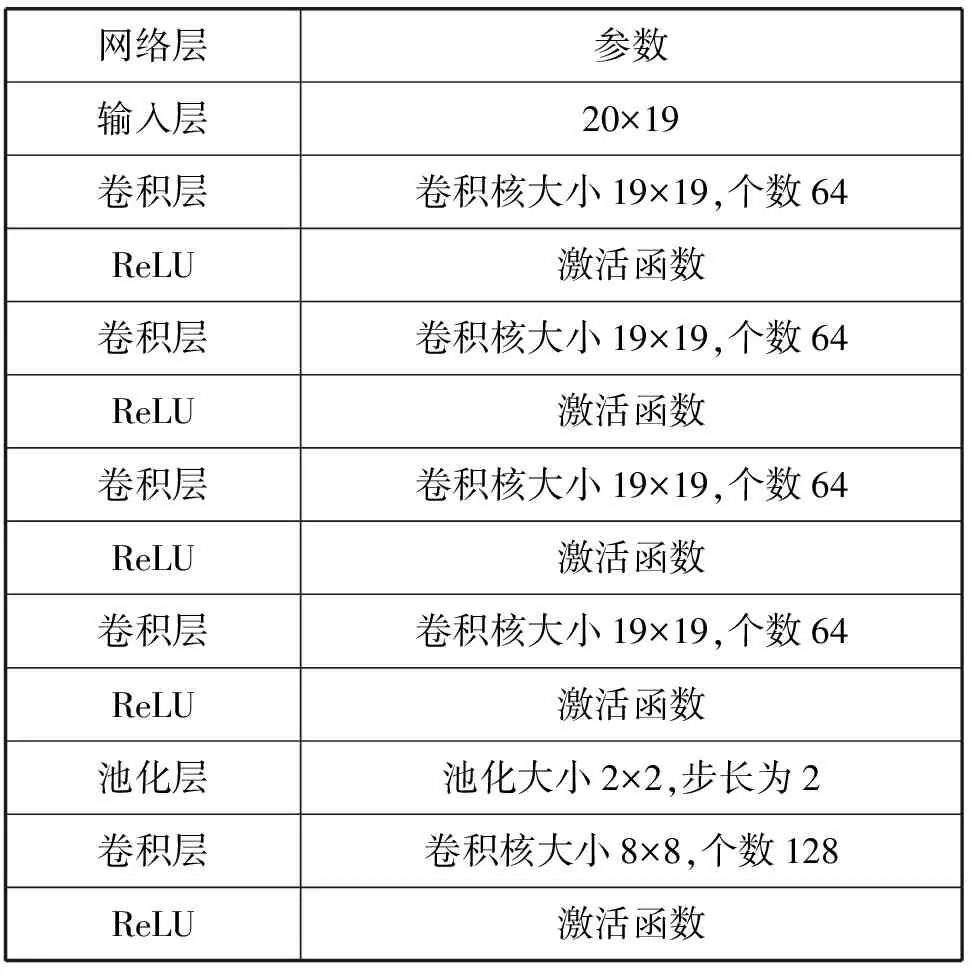
表7 19窗口下的网络模型

续表7

为了评估本文模型的准确率，采用六种公开的测试集(CASP9、CASP10、CASP11、CASP12、CB513和25PDB)进行测试。本文模型与SPINE-X[26]、SSpro[27]、PSIPRED[28]、RaptorX-SS8[29]和DeepCNF[30]模型一样(其中SPINE-X、SSpro、PSIPRED、RaptorX-SS8和DeepCNF方法在测试集上的结果均摘自文献[30])，采用3类蛋白质二级结构预测准确率作为评价本文模型的指标，在数据集CASP10、CASP11、CB513上进行对比，结果如表8所示。SPINE-X使用多步神经网络，SSpro采用双向朴素递归神经网络，PSIPRED使用两层前馈神经网络，RaptorX-SS8使用条件神经场，DeepCNF是深度神经网络和条件神经场相结合。

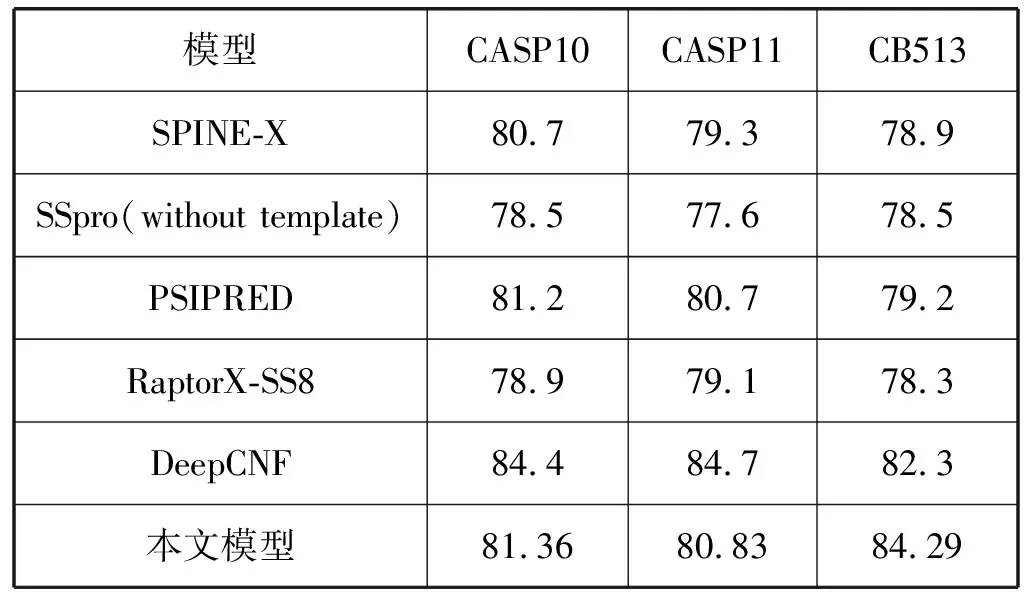
表8 3个数据集上各模型预测准确率对比

由表8可以看出，相比SPINE-X、SSpro、PSIPRE和RaptorX-SS8模型，本文模型在3组蛋白质数据集上的3类蛋白质二级结构预测准确率有了提高，可以证明通过贝叶斯自动优化的卷积神经网络能够很好地提取蛋白质序列的特征，提高了蛋白质二级结构预测性能。本文模型在CB513数据集上准确率均要高于其他方法，但是在CASP10、CASP11数据集上要低于DeepCNF模型，主要原因可能是DeepCNF结合条件随机场，考虑氨基酸残基与标签的关系来得到全局的最优解。

3 结 语

蛋白质二级结构预测是生物信息学中的一项重要工作，对研究蛋白质的结构和功能有着极其深远的意义。本文融合了卷积神经网络和贝叶斯优化模型，自动优化卷积神经网络的网络层数、学习率、梯度冲量和正则化系数，并应用到蛋白质3类二级结构预测中。通过优化后的卷积神经网络提取氨基酸残基之间的局部特征进行蛋白质二级结构预测。实验结果表明，本文模型能够提高蛋白质3类二级结构预测准确率。在未来的工作中，将会结合氨基酸局部和远程特征来进行蛋白质二级结构预测。