一种基于进化博弈理论的虚拟机部署算法
乐 艺
(南京城市职业学院 江苏 南京 210002)
0 引 言
对于云供应商而言,部署应用使其维持相应的资源利用率(CPU资源和带宽资源)和功耗的同时,满足期望的性能等级(响应时间)是当前在云端部署应用任务必须解决的问题[1]。为了确保上述需求,需要通过考虑多个不同的条件,如负载和资源可用性等,调整应用的部署目标和资源分配方案,进而动态地对应用进行重部署。本文将重点关注云端应用部署的适应性和稳定性。适应性即根据给定目标的上下文环境,调整应用的部署位置和资源分配;稳定性指对于应用的部署方案和资源分配方案,应尽量最小化方案决策的波动。
为了实现云端应用的自适应和稳定性的部署策略,本文提出一种基于进化博弈理论的云应用部署算法。本文算法的每个应用维持一个应用部署策略集合(即一个种群),其中每个策略表示应用的部署位置和资源分配。可以确保通过部署策略间的一系列进化博弈过程[2],种群状态(策略分布)可以收敛至一种与初始状态无关的进化稳定均衡上。进化稳定种群状态中的占优策略称为进化稳定策略。在该状态下,除了进化稳定策略之外,没有任一其他策略可以占优整个种群。在给定该理论性质前提下,算法可以以稳定的方式利用进化稳定策略将云应用部署策略运行于稳定状态。
1 相关工作
许多研究工作已经在云计算应用部署方面展开,其多数工作所考虑的应用为单层次的应用体系结构,大多考虑单目标优化,例如文献[3-6]均只考虑了能耗节省一个目标。相比而言,本文算法考虑的是一种多层次的应用体系,考虑了多目标的同步优化,且可以在多个冲突目标间寻找平衡。
目前,博弈论方法已经被用于云计算的诸多方面,如应用部署[7-9]、任务分配[10]及数据副本调度[11]等。文献[7-9]将基于贪婪思想的算法用于寻找应用部署问题的均衡解,但贪婪思想并不能确保所达到的部署均衡解具有好的稳定性。而本文算法将通过进化博弈中的复制动态机制确保得到的均衡解是具有渐近稳定性的。
遗传算法[12-13]和其他随机式优化算法[14-15]也可用于求解云计算中的应用部署问题。这些算法虽然可以寻找最优部署解,但也无法保证其稳定性。相比而言,本文算法将寻找进化稳定解,并验证其解可以收敛在均衡解上。
文献[16]的工作与本文有些类似,但本文在问题形式化上对其进行了扩充。本文在其基础上另外加入了带宽分配和功耗两个目标优化,同时在每个部署策略中考虑了带宽分配参数,这与实际的云计算环境中需要考虑的问题也更加贴近。同时,本文在仿真环境中进行大量实际应用负载的仿真实验,可以更加准确地评估与测试算法的性能。
2 问题描述
本节对云应用部署问题做形式化描述。假设现有M台主机用于部署N个云应用,每个应用设计为三层服务器模型,即每个应用的执行需要按序通过外层的Web服务器、中间的应用服务器及后台的数据库服务器,然后通过后台服务器返回至外层的Web前台显示应用执行结果,该模型如图1所示。其中:Web服务器接收应用任务的HTTP消息,验证消息中的数据并向提交应用的用户提供Web用户接口;APP应用服务器执行相应功能的应用逻辑并处理用户提交的数据;Database数据库服务器则进行数据访问与存储。每条消息顺序地从Web服务器通过应用服务器到数据库服务器进行处理,响应消息则反向从数据库服务器返回。本文假设不同的云应用利用不同的服务器集合,且服务器在不同应用间不进行共享。每台服务器假设运行于一台主机的虚拟机上,且一台主机可以运行多台虚拟机,它们可以共享本地主机上的可用资源。
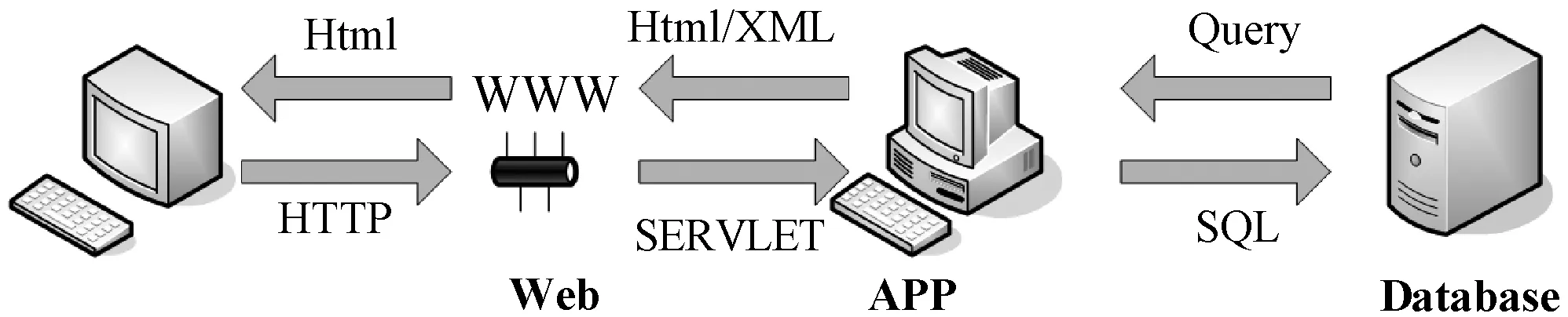
图1 应用执行的三层模型
云应用部署问题的目标是寻找一种进化稳定策略,该策略将N个应用(即N×3台虚拟机)部署于M台主机上,使得对于给定的负载条件和可用资源下,应用能够适应其部署位置和资源分配,并实现以下相关目标的最小化。
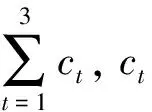

3) 响应时间表示消息从Web服务器传输至数据库服务器间所需要的时间,表示为Tp+Tw+Tc,其中:Tp表示应用在三台服务器上处理用户发出消息的总时间,Tw表示消息在服务器上等待处理的时间,Tc表示消息在服务器传输的总延时。Tp、Tw和Tc三者通过M/M/1队列模型估算,应用的消息到达服从泊松分布,服务器的消息处理时间按指数分布。
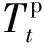
(1)
Tw计算方法如下:
(2)
(3)
式中:λ表示一个应用的消息到达率,即在单位时间内应用接收来自于用户的消息数量;ρt表示第t层服务器的CPU利用率;fmax表示主机的最大CPU频率;ft表示第t层服务器寄宿的主机的CPU频率。
Tc计算方法如下:
(4)
t′=t+1
4) 功耗表示应用执行过程中主机运行三台虚拟机时的总体功耗,单位为W,定义为:
(5)
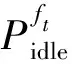
将CPU能力约束考虑为:对于所有M台主机,wi≤1,wi表示分配给第i台主机的总CPU时间份额。该约束的违例条件可计算为:
(6)
若wi>1,则Ii=1;否则,Ii=0。
考虑的带宽能力约束为:对于所有的M台主机,yi≤1,yi表示分配给第i台主机的总带宽量(百分比形式表示)。该约束的违例条件可计算为:
(7)
若yi>1,则Ii=1;否则,Ii=0。
3 进化博弈理论
对于传统的博弈论而言,博弈者的目标是选择一个使其收益最大化的策略。相比而言,进化博弈是种群中博弈者随机式重复的博弈过程。本节介绍进化博弈的两个关键要素:进化稳定策略ESS和复制动态。
3.1 进化稳定策略ESS
假设初始种群中所有博弈者的博弈策略为k,有一小部分种群的博弈者比例为x,x∈(0,1),其出现策略变异,执行不同的变异策略l。当一个博弈者参与到博弈过程中时,其对手执行策略k和l的比例分别为1-x和x。因此,执行策略k和l的博弈者的期望收益分别为U(k,xl+(1-x)k)和U(l,xl+(1-x)k)。
定义1一个策略k为进化稳定策略,若对于每个策略l≠k,存在一个确定的x′∈(0,1),使得对于所有的x∈(0,x′),如式(8)所示的不等式恒成立。
U(k,xl+(1-x)k)>U(l,xl+(1-x)k)
(8)
如果支付函数为线性,则由式(8)可推出:
(1-x)U(k,k)+xU(k,l)>(1-x)U(l,k)+xU(l,l)
(9)
如果x接近于0,则由式(9)可推导出:
U(k,k)>U(k,l)或U(k,k)=U(l,k)且U(k,l)>U(l,l)
(10)
这表明采用策略k的博弈者会得到比采用其他策略的博弈者更高的收益。因此,没有任一博弈者可以通过从策略k改变至其他策略上而获得更高的收益,这表明进化稳定策略是处于纳什均衡的一个解。而进化稳定策略也是拥有更低种群份额的任意变异策略无法入侵的策略。
3.2 复制动态
复制动态用于描述采用不同策略的种群随时间发生变化的情况。令λk(t)≥0为采用策略k∈K的博弈者数量,K表示可行策略集合。博弈者的总的种群数量可表示为:
(11)
令xk(t)=λk(t)/λ(t)表示在时间t时采用策略k的博弈者的种群份额。种群状态定义为X(t)={x1(t),x2(t),…,xk(t),…,xK(t)}。给定X,采用策略k的期望收益定义为U(k,X)。种群的平均收益表示为:
(12)
在复制动态中,种群份额xk的动态可作如下描述:
(13)
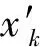
定理1若策略k为严格占优策略,则xk(t)t→∞→0。
若策略得到的收益严格高于任一博弈对手的收益,则认为该策略是严格占优策略。随着占优策略的种群份额增加,最后将占优整个种群。相反地,若策略收益严格低于采用严格占优策略的博弈者,则该策略被称为严格被占优策略。因此,严格被占优策略在种群中会随着时间逐渐消失。
纳什均衡与复制动态的稳定状态间联系密切,其稳定状态下的种群份额将不会随着时间而发生改变。由于处于纳什均衡时没有博弈者会改变其策略,复制动态中的每一个纳什均衡都将是一种稳定状态。如前文所述,一个进化稳定策略是一个纳什均衡处的一个解,因此,进化稳定策略即为复制动态中处于稳定状态的一个解。换言之,进化稳定策略是种群中处于稳定状态的严格占优策略。
本文算法目标就是对每个应用维持一个部署策略的种群,每个种群中策略被随机选取,博弈者间进行重复博弈直到种群状态达到一种稳定状态,即部署算法可以找到种群的严格占优策略,并根据该策略(进化稳定策略ESS)完成虚拟机部署。
4 算法设计
将N个云应用定义为N个种群,表示为{P1,P2,…,PN},每个种群在策略间进行博弈。将策略s定义为应用中三台虚拟机的部署位置和资源分配解,表示为:
(14)
式中:ai表示第i个应用;hi,t表示执行应用ai的第t层虚拟机的主机ID;ci,t表示应用ai的第t层虚拟机的CPU份额分配;bi,t表示应用ai的第t层虚拟机的带宽分配;fi,t表示主机hi,t的CPU频率。图2所示为两个应用a1和a2的两种示例策略,N=2,M=3,图中:应用a1的策略s(a1)将第一层虚拟机VM部署于主机1上,即h1,1=1,其运行于1 GHz的CPU频率,虚拟机消耗30%的CPU份额和80 Kbit/s带宽,即c1,1=30,b1,1=80;第二层虚拟机部署于主机1,即h1,2=1,其消耗了30%的CPU份额和85 Kbit/s带宽,即c1,2=30,b1,2=85;第三层虚拟机部署于主机2,即h1,3=2,其运行于2 GHz的CPU频率,虚拟机消耗45%的CPU份额和120 Kbit/s带宽,即c1,3=45,b1,3=120。给定s(a1),应用a1在CPU分配和带宽分配上的目标值为105%和285 Kbit/s。

图2 部署策略示例
算法1所示为本文算法通过进化博弈使每个应用寻找进化稳定策略的过程。
算法1基于进化博弈的虚拟机部署算法
1.g=0
2. randomly generate the initialNpopulations forNapplications:P={P1,P2,…,PN}
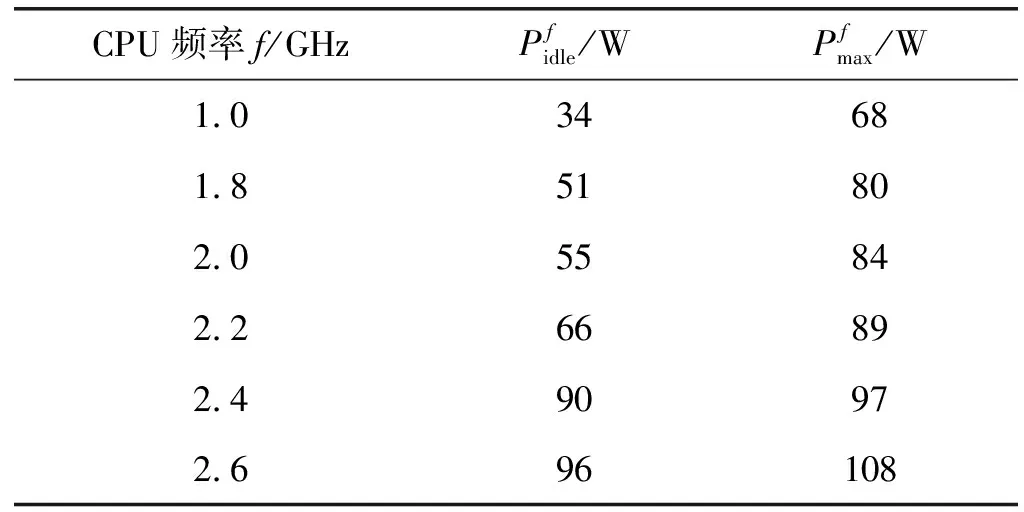
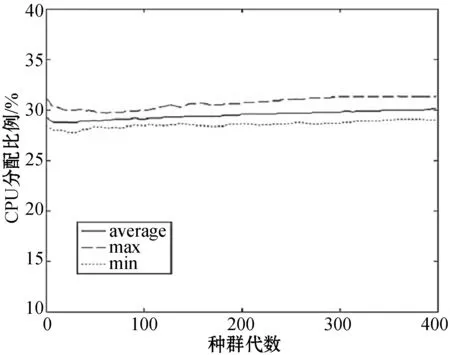
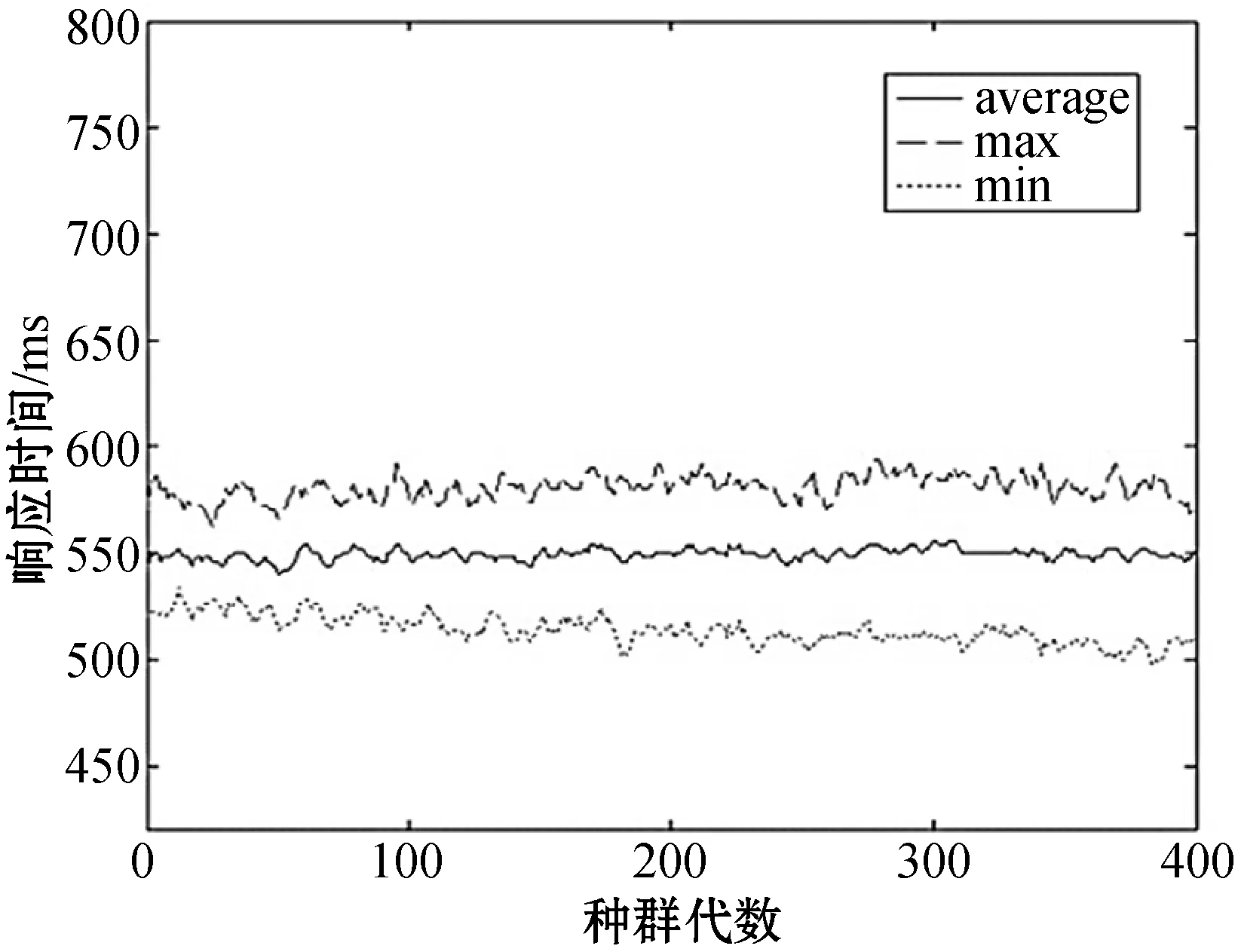
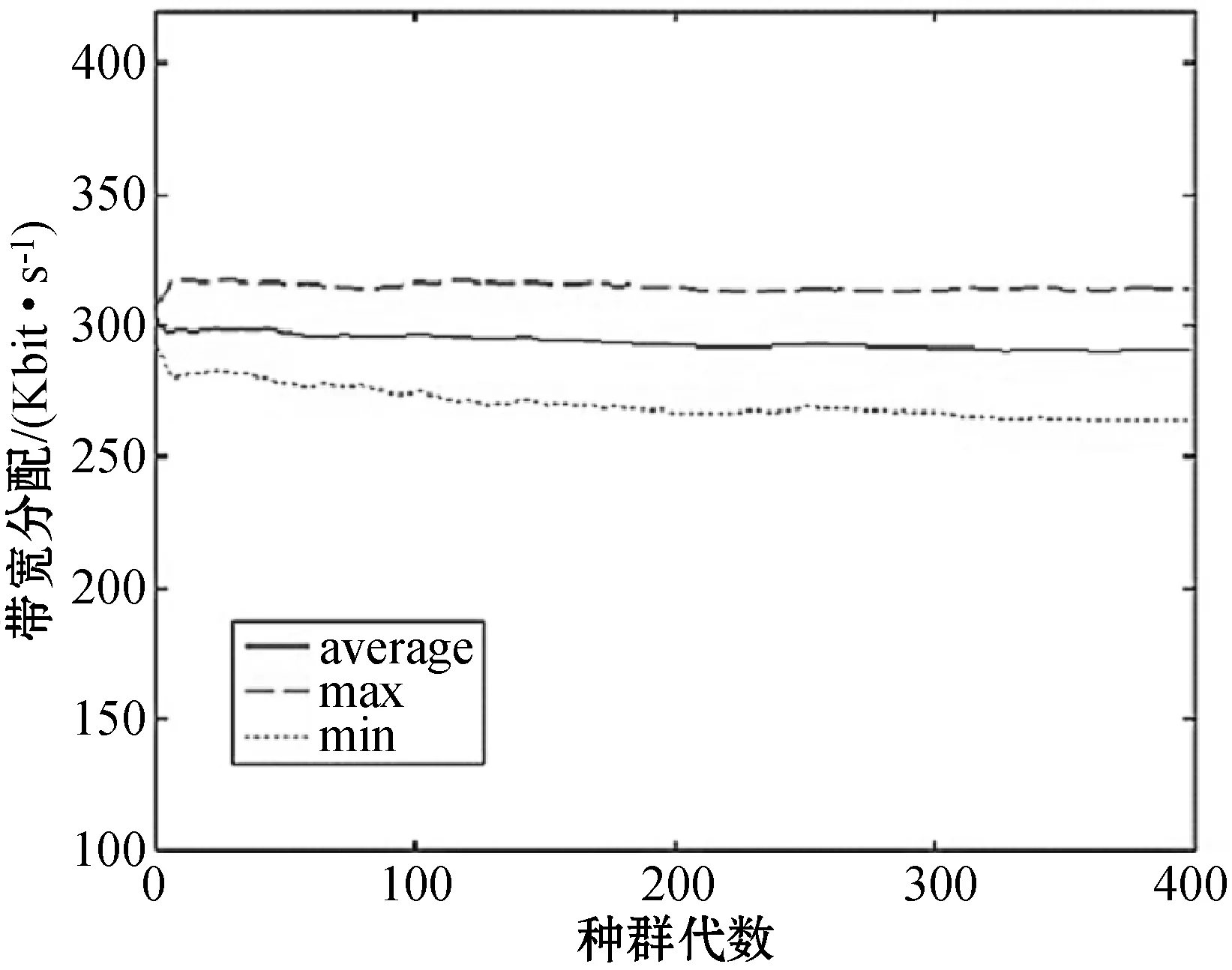
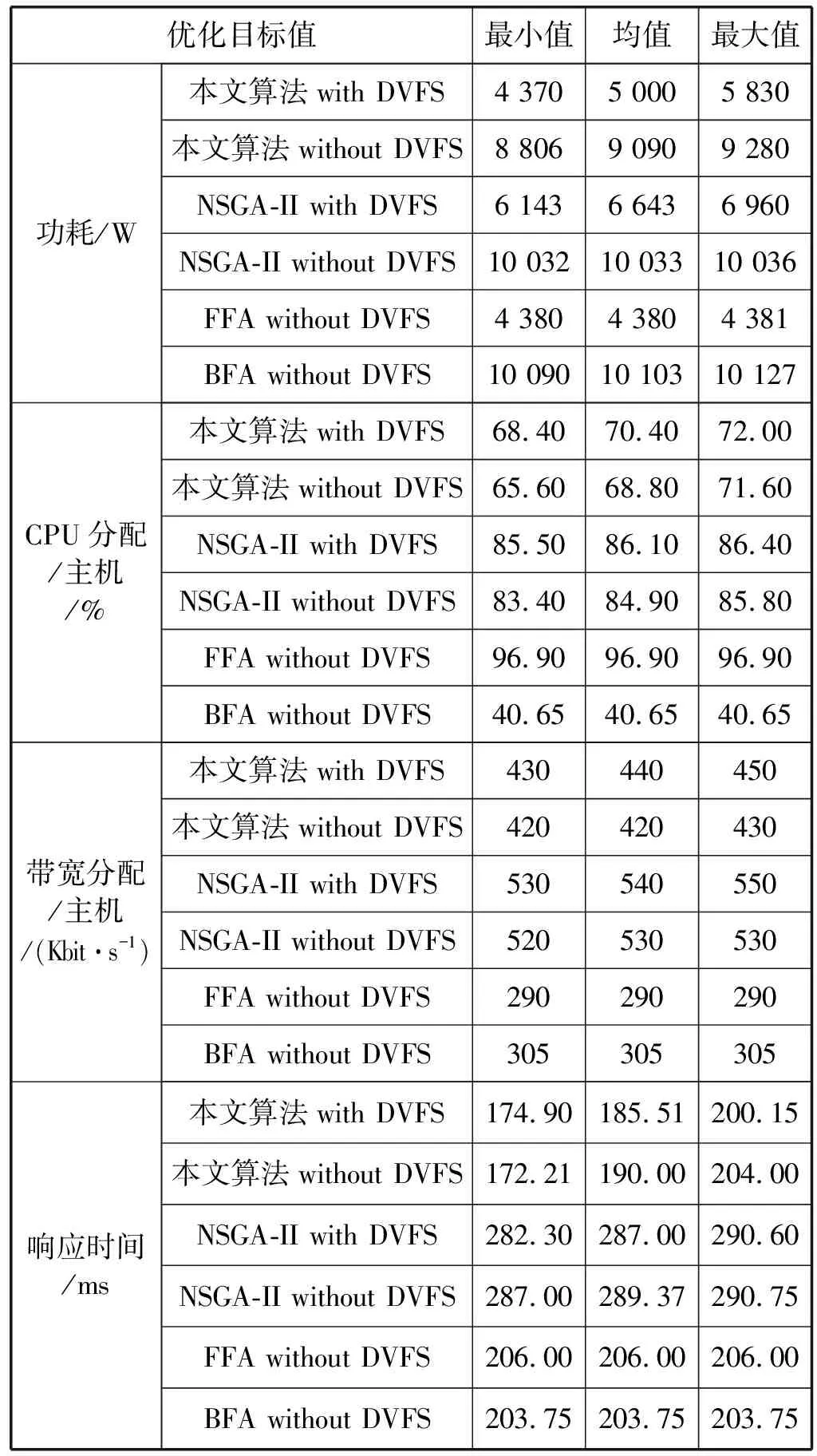
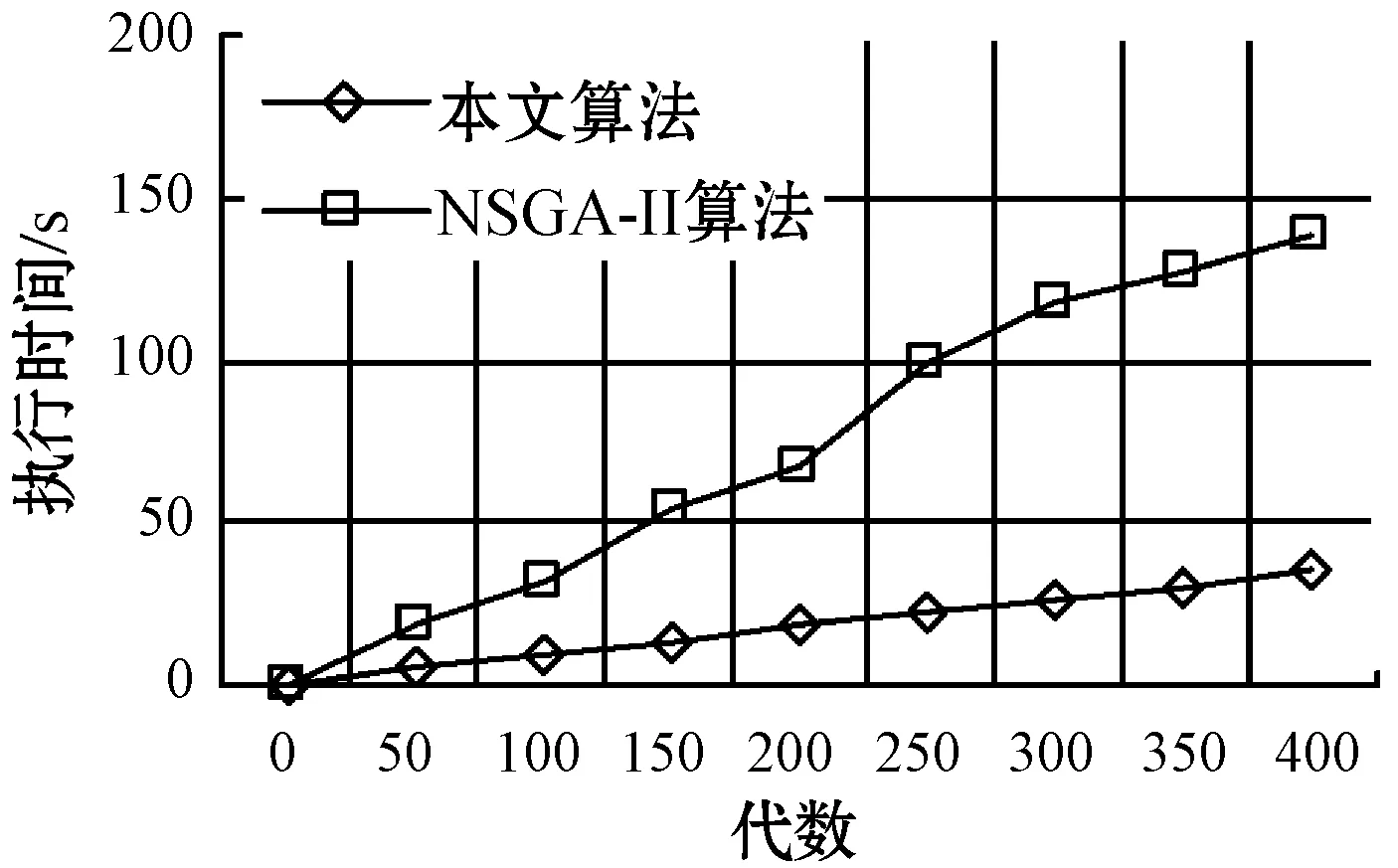
3.whileg 4.foreach populationPirandomly selected fromPdo 6.forj=1 to |Pi|/2do 7.s1←randomlySelect(Pi) 8.s2←randomlySelect(Pi) 9.winner←performGame(s1,s2) 10.replica←replicate(winner) 11.ifrandom()≤Pmthen 12.replica←mutate(winner) 13.endif 14.Pi{s1,s2} 16.endfor 19.whilediis infeasibledo 20.Pi{di} 22.endwhile 23.deploy VMs for the current application based ondi 24.endfor 25.g=g+1 26.endwhile 算法1在初始第0代种群时,针对N个应用随机方式生成N个种群,即N个策略,即步骤1-步骤2。在第g代种群中,每个种群实施系列博弈,即步骤4-步骤24。单次博弈随机选择策略对s1和s2,根据前文中描述的目标函数,得到两个策略间的胜者策略和败者策略,即步骤7-步骤9。将败者策略从种群中移除,胜者策略被复制以增加其种群份额,并以概率Pm进行变异,即步骤10-步骤15。变异操作随机从胜者种群中选择三台虚拟机中的一台,并随机变换其h值,即步骤12。 一旦种群中的所有策略参与博弈,算法即识别可行策略,其种群份额xs为最高,并将其作为一个占优策略di,即步骤18-步骤22。若策略从不违背CPU和带宽能力的约束,则可认为该策略为可行策略。算法根据占优策略部署应用的三台虚拟机。 算法1步骤9的performGame()中,博弈胜者的选择取决于给定的两个策略的占优关系及其可行性。定义一个策略s1占优另一个策略s2,表示为s1>s2,当且仅当:(1)s1的目标值优于或等于s2的所有目标值;(2)s1的目标值优于s2的至少一个目标值。 本节分析算法的稳定性,即通过证明每个种群的状态是否收敛至一个进化稳定均衡上分析算法是否能够达到至少一个纳什均衡上。稳定性分析包括三个步骤:1) 设计描述种群状态动态的差分等式;2) 证明策略选择过程存在均衡;3) 证明均衡是渐近稳定或进化稳定的。先对稳定性分析中使用的符号含义作出如下说明: S代表可行策略集合,S*代表种群中出现的一个策略集合。 X(t)={x1(t),x2(t),…,x|S*|(t)}代表时间t时的种群状态,其中xs(t)表示采用策略s∈S的种群份额,且: (15) Fs代表策略s的适应度值,该值是根据不同博弈者之间的占优关系决定的相对值,博弈胜者比败者拥有更高的适应度值。 (16) 注意:若策略s为严格占优策略,则xs(t)t→∞→0。 定理2种群状态收敛于均衡上。 证明:不同的策略拥有不同的适应度值,换言之,所有策略中仅有一个策略拥有最高适应度值。根据定理1,假设F1>F2>…>F|S*|,则种群状态将收敛于均衡,即:X(t)t→∞={x1(t),x2(t),…,x|S*|(t)}t→∞={1,0,…,0}。证毕。 定理3定理2中得到的均衡是渐近稳定的。 证明:在均衡X={1,0,…,0}处,差分等式集合可通过替换x1=1-x2-…-x|S*|进行缩小: (17) 式中:csk≡Φ(Fs-Fk)-Φ(Fk-Fs),且Z(t)={z2(t),z3(t),…,z|S*|(t)},表示缩小后的对应种群状态。根据定理1,在(|S*|-1)维度下,Zt→∞(t)=Zeq={0,0,…,0}。 如果所有Z(t)的雅可比矩阵的特征值拥有负的实数值部分,则Zeq是渐近稳定的。雅可比矩阵J的元素为: (18) 因此,J可以作如下定义: (19) 对于所有s,cs1=-Φ(F1-Fs),Zeq={0,0,…,0}是渐近稳定的。证毕。 本节通过仿真实验验证算法的适应性和稳定性。利用CLOUDSIM构建云计算环境,建立的云数据中心仿真环境由100台主机组成,即M=100,主机分布于10×10的网格拓扑结构中。假设执行5种类型的云应用,表1给出了5种应用的消息到达率(即每秒到达的消息数)和消息在不同服务器上的处理时间(单位为秒)。仿真实验中针对每种应用类型执行40个实用实例,即一共执行200个应用实例,N=200。 表1 应用类型及其属性 假设每台主机配置AMD皓龙2218型CPU,该CPU拥有6种运行频率/电压组合,表2给出了在CPU利用率为0%和100%时每种频率/电压组合下的功耗,该参数配置可用于计算功耗目标值。 表2 CPU可运行的频率状态及功耗 算法设置每个种群的策略数为100,算法1中的变异概率Pm设置为0.01,算法的最大种群代数Gmax设置为400,每个仿真结果选取独立的20次仿真结果的平均值。 图3所示为四个优化目标同步考虑时得到的目标值的性能表现情况,图中统计了单个目标值的最大值、最小值和平均值随着种群代数增加的变化情况。可见,本文算法较好地均衡了不同目标值,使得算法在CPU的分配、响应时间、带宽分配及功耗方面取得了较好的性能均衡。 (a) CPU分配 (b) 响应时间 (c) 带宽分配 (d) 功耗 表3所示为本文算法与经典进化多目标遗传算法NSGA-II、首次适应算法FFA、最佳适应算法BFA的比较结果。表3给出了最后一个种群代数中优化目标值的最小值、平均值和最大值。在所有的目标中,本文算法均优于NSGA-II算法,性能的最大差异出现在CPU未使用DVFS时的最小带宽分配结果上,性能差异约为40%,而性能的最小差异则出现在CPU使用DVFS时的最大响应时间上,性能差异约为16.6%。平均来说,本文算法的性能优于NSGA-II算法为24.19%。若CPU不使用DVFS技术,FFA算法拥有最低的功耗,由于该算法的设计宗旨是以最小化利用主机数量部署虚拟机为目标的,因此在其他目标上表现不佳。BFA算法在CPU分配方面是最优的,但在功耗方面表现最差,原因在于该算法在主机上部署虚拟机是寻找最适宜的主机,使得剩余资源具有更高的可用性。本文算法兼顾考虑了四个目标值,获得了处于FFA和BFA之间更为均衡的目标值,并在响应时间和带宽分配上获得了最优的性能表现。 表3 性能比较 表4所示为20次不同的仿真实验中在最后一代种群中本文算法和NSGA-II算法在目标值上的方差,越低的方差表明在目标值上更好的稳定性(即不同仿真实验下目标值上更小的波动)。显然,本文算法比NSGA-II算法维持了更连续和更高的稳定性,其平均稳定性为29.32%,高于NSGA-II算法。该结果表明,本文算法相较NSGA-II算法具有稳定属性,因为本文算法可以找到部署方案的进化稳定策略ESS。 表4 两种算法在目标值上的稳定性 图4是本文算法与NSGA-II算法在不同种群代数下算法执行时间的性能表现。可以看到,本文算法的执行比NSGA-II算法快约74.1%,可见本文的进化博弈方法不仅可以在目标值的同步优化取得较好的效果,而且算法的执行效率也较高。 图4 计算代价比较 为了实现云环境中自适应性和稳定性的应用执行与部署,本文提出了一种基于进化博弈理论的多目标虚拟机部署算法。该算法可以确保每个云应用找到一种进化稳定部署策略,在该策略下,对于给定的系统负载和资源可用性,应用可确定其部署位置和相应资源分配,证明了种群状态可收敛于部署策略的进化稳定策略ESS上,且得到的均衡解是渐近稳定的。结果表明,在响应时间、资源利用率、功耗等指标上,该算法均表现出较好的性能。

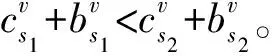
5 稳定性分析
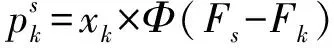
6 仿真实验



7 结 语

