形状因子及复杂结构井拟稳态流动阶段井底压力渐近解的计算方法

徐有杰 刘启国 李晓平 杨思涵 张 楷 谭晓华

1.“油气藏地质及开发工程”国家重点实验室·西南石油大学 2.中国石油西南油气田公司勘探开发研究院

0 引言

油气藏形状位置因子（以下简称形状因子）是影响油气井拟稳态流动阶段井底压力渐近解及产能指数的重要参数，从而会对油气井生产动态预测结果产生直接影响。1954年，Matthews等[1]基于压力恢复试井解释方法，得到了矩形封闭油藏平均地层压力随时间的变化曲线。基于该方法，Dietz[2]推导出不同边界形状因子计算式，并且确定了拟稳态流动开始的时间。上述两位学者在计算形状因子时，都是假定油气井以定产量进行生产。Ozkan等[3]针对常规直井、水平井和无限导流压裂直井，采用解析解的方法，得到了圆形和矩形封闭形状因子计算式。然而，上述学者仅仅给出了油气井定产量生产条件下形状因子的计算方法。1998年，Helmy等[4]推导出油气井定压生产条件下的形状因子计算方法，并与Dietz[2]计算的形状因子（以下简称Dietz形状因子）进行对比，发现在油气井定产量生产条件下的形状因子大于定压生产条件下的形状因子。2005年，Haryanto[5]采用数值模拟方法计算了有限导流压裂直井定压生产条件下的形状因子，并且分析了形状因子与导流能力的关系。

对于一些简单井型，采用解析解的方法求取拟稳态流动阶段井底压力渐近解较容易，但是对于一些复杂结构井（多段压裂水平井、多分支水平井等）[6]，则难度较大。因此，寻求一种实用、有效的形状因子计算方法，对于准确获取复杂结构井拟稳态流动阶段井底压力渐近解及产能指数具有重要意义。为此，笔者针对不同形状封闭边界油气藏中直井，根据试井分析曲线——压力及压力导数曲线之间的关系，重新计算形状因子，并且与Dietz形状因子进行对比；在此基础上，推导出复杂结构井拟稳态流动阶段井底压力渐近解，并且进行验证，进而绘制Blasingame递减曲线典型图版。

1 矩形封闭边界油气藏直井井底压力解

假设矩形封闭边界油气藏中有一口定产量生产的直井，该井所处位置如图1所示，图中L1、L2、L3、L4分别表示井距离矩形封闭油气藏上、左、下、右边界的距离，xe、ye分别表示矩形封闭边界油气藏长度与宽度；流体在储层中的流动满足达西渗流规律，流体温度保持恒定；忽略毛细管力和重力的影响。

基于点源函数法，Ozkan等[7]推导出无限大外边界油气藏在Laplace空间任意位置的压力解，即

其中

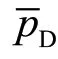
根据镜像反映法，得到矩形封闭边界油气藏所有镜像井的井底压力解，即

其中

矩形封闭边界油气藏中直井井底压力解为式（1）、（2）之和，即

通过Stehfest数值反演，计算得到矩形封闭边界油气藏中直井在实空间的井底压力解，进而绘制井底压力与压力导数曲线。

2 形状因子计算及验证

对于圆形封闭边界油气藏，处于拟稳态流动阶段的直井井底压力渐近解为[4]：

式中pwD表示实空间无因次井底压力或拟压力；tDA表示基于油气藏面积定义的无因次时间；A表示油气藏面积，cm2；γ表示欧拉常数；CA表示形状因子，无量纲；rw表示井筒半径，cm。

根据试井分析曲线——压力及压力导数曲线可以进行流动阶段划分。而由式（4）看出，可以将等式右边第2项看作油气井拟稳态流动阶段pwD和p'wDtDA之差，因此，对式（4）关于lntDA求导，pwD和p'wDtDA之差即是拟稳态流动阶段井底压力渐近解系数，即

式中bDpss表示拟稳态流动阶段井底压力渐近解系数，该数值与井结构、边界大小及形状等因素有关。

可以看出，通过计算拟稳态流动阶段pwD和p'wDtDA之差，可以反求圆形封闭边界形状因子。若井位于矩形封闭边界油气藏中，可以采取同样的方法求得形状因子。

下面以圆形封闭边界油气藏为例，验证笔者提出的形状因子计算方法的准确性。假设一口直井处于油气藏中心位置，外边界半径为5 000 m，井筒半径为0.1 m。

如图2所示，图中蓝色线对应拟稳态流动阶段，该阶段直井pwD和p'wDtDA的差值为10.070，则bDpss为10.070。对于圆形封闭边界油藏，Dietz形状因子为31.600。基于本文方法，计算形状因子（CA），有

可以看出，对于圆形封闭边界油气藏中心的一口直井，采用本文方法计算得到的形状因子与Dietz形状因子的相对误差在1%以内。然后，针对不同形状封闭边界油气藏中直井，将采用本文方法计算的形状因子与Dietz形状因子对比，结果非常接近（表1），进一步验证了本文方法的准确性，同时计算出拟稳态流动阶段开始的无因次时间（tDpss），其计算式为：

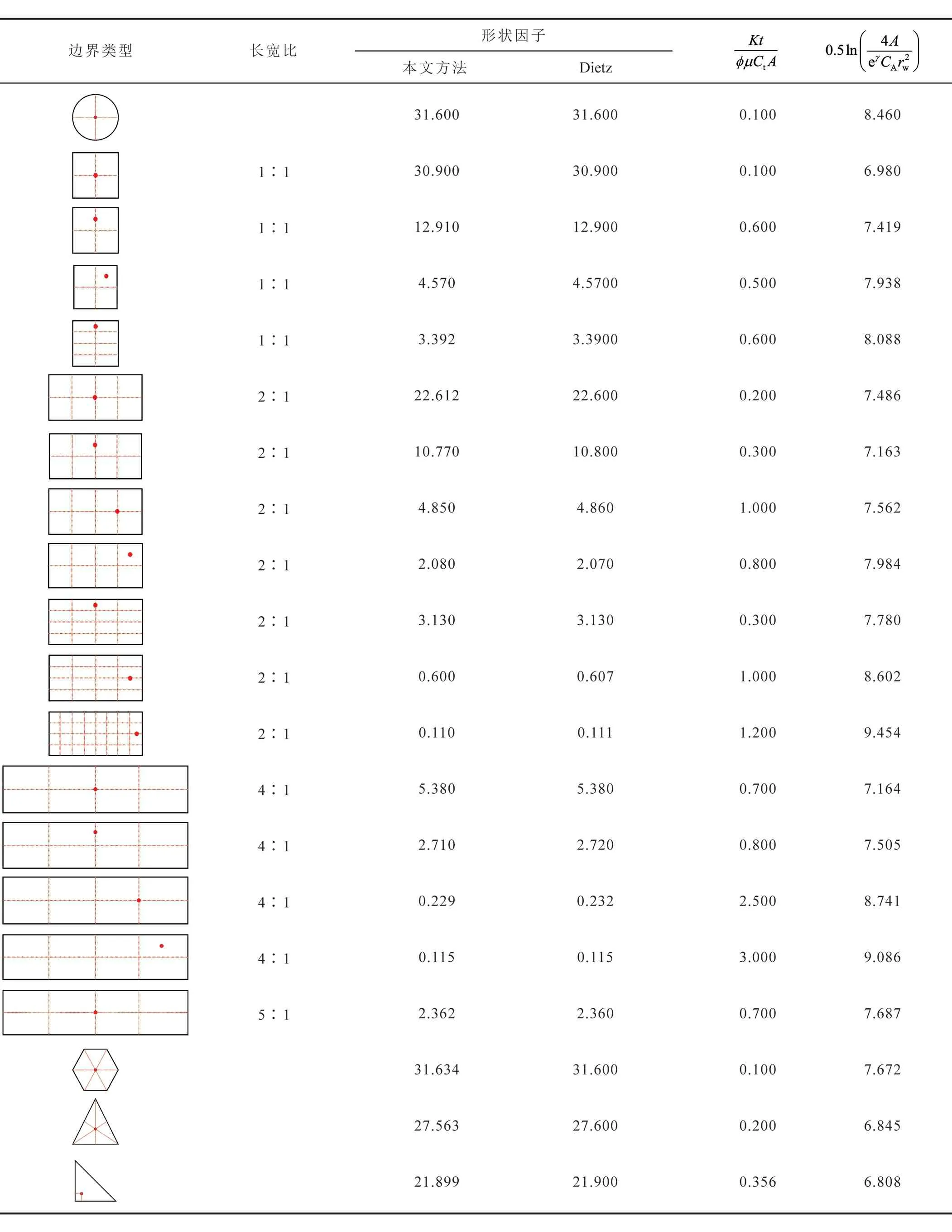
表1 不同形状封闭边界条件下形状因子计算结果对比表

式中K表示储层渗透率，D；t表示生产时间，s；表示储层孔隙度；μ表示流体黏度，mPa·s；Ct表示综合压缩系数，10MPa－1。

3 复杂结构井拟稳态流动阶段井底压力渐近解及其验证

计算形状因子的主要目的是为了计算拟稳态流动阶段井底压力渐近解，那么，既然利用pwD和p'wDtDA之差可以计算形状因子，那么就可以利用pwD和p'wDtDA之差计算拟稳态流动阶段井底压力渐近解。对于常规直井（含压裂直井）、水平井，可以通过公式简化，得到实空间井底压力渐近解，但是对于复杂结构井（如多段压裂水平井、多分支井等），则无

法通过解析反演的方法直接得到拟稳态流动阶段井底压力渐近解，从而无法对Blasingame递减分析方法的物质平衡时间进行准确计算，进而无法准确计算复杂结构井的单井控制储量。

基于前面直井拟稳态流动阶段井底压力渐近解结构，对于复杂结构井，可以采用同样的方法计算复杂结构井拟稳态流动阶段井底压力渐近解。因此，通过求取复杂结构井拟稳态流动阶段pwD和p'wDtDA之差，即求得复杂结构井的bDpss，从而可以获得复杂结构井拟稳态流动阶段井底压力渐近解，即

式中pwDps表示拟稳态流动阶段无因次井底压力。

下面分别对不同边界油气藏中复杂结构井井底压力渐近解进行验证。

3.1 圆形封闭边界油气藏＋大斜度井

Cinco-Ley等[8]、Ozkan等[9]分别给出了均质油气藏中大斜度井在实空间和Laplace空间的井底压力计算式。姜瑞忠等[10]考虑储层渗透率应力敏感和启动压力梯度等因素，建立双重介质大斜度井试井数学模型并分析各参数对试井曲线的影响。任俊杰等[11]建立三重介质油气藏大斜度井试井数学模型并且给出了对应的井底压力响应曲线。借鉴前人的研究成果，笔者此次计算得到均质、圆形封闭边界油气藏中大斜度井井底压力及其导数，求得两者之差，然后，通过拟稳态流动阶段无因次井底压力与压力导数差来验证本文方法的准确性，其中无因次变量的定义见本文参考文献[9]，此处不再赘述。

图3分别绘制出圆形封闭边界油气藏大斜度井（pwD－p'wDtDA）—tDA和（pwD－pwDps）—tDA曲线，图中hD表示无因次储层厚度。可以看出，在压力波未到达封闭边界之前，（pwD－p'wDtD）随tDA增大而增大，当压力波到达封闭边界以后，（pwDp'wDtD）为一定值，该数值即对应式（8）中bDpss的数值。求得bDpss，即得到了大斜度井拟稳态流动阶段井底压力渐近解。绘制（pwD－pwDps）—tDA曲线，如图3所示，在压力波未到达封闭边界之前，（pwDpwDps）随tDA增大而减小，当压力波到达封闭边界以后，（pwD－pwDps）为0，从而证实利用本文方法计算的拟稳态流动阶段井底压力渐近解（pwDps）是正确的。

另外，基于本文方法还可以计算大斜度井拟表皮因子。关于大斜度井拟表皮因子的计算，参见本文参考文献[12-14]。根据Rogers等[15]的研究，大斜度井拟稳态流动阶段井底压力解与完全射开的直井拟稳态流动阶段井底压力解的差即为大斜度井拟表皮因子。基于本文方法，分别计算井斜角为50°、60°、75°，hD为100、200、500、1 000、2 000、5 000条件下大斜度井拟表皮因子（图4红点），然后将计算结果与Ozkan等[9]计算的大斜度井拟表皮因子（图4实线）相比，相对误差在1%以内，验证了本文方法的准确性。

3.2 圆形封闭边界油气藏＋有限导流压裂直井

Pratikno等[16]推导出圆形封闭边界油气藏中有限导流压裂直井拟稳态流动阶段井底压力渐近解，有限导流压裂直井的bDpss计算式为：

其中

u=lnCfD

a1=0.936 268 00

a2=－1.004 890 00

a3=0.319 733 00

a4=－0.042 353 20

a5=0.002 217 99

b1=－0.385 539 00

b2=－0.069 886 50

b3=－0.048 465 30

b4=－0.008 135 58

式中ReD表示无因次圆形封闭边界的半径；CfD表示无因次裂缝导流能力。

图5分别绘制出圆形封闭边界油气藏有限导流压裂直井（pwD－p'wDtDA）—tDA和（pwD－pwDps）—tDA曲线，可以看出，在压力波未到达封闭边界以前，（pwD－p'wDtDA）随tDA增大而增大，当压力波到达封闭边界以后，（pwD－p'wDtDA）为一定值，该数值即对应式（8）中bDpss的数值。求得bDpss，即得到了有限导流压裂直井拟稳态流动阶段井底压力渐近解。绘制（pwD－pwDps）—tDA曲线，如图5所示，在压力波未到达封闭边界之前，（pwD－pwDps）随tDA增大而减小，当压力波到达封闭边界以后，（pwDpwDps）为0，从而证实利用本文方法计算的拟稳态流动阶段井底压力渐近解（pwDps）是正确的。

再利用Pratikno等[16]计算的bDpss与采用本文方法计算的bDpss进行对比，发现裂缝导流能力无论如何变化，两种方法计算的bDpss相对误差都很小（表2），完全能够满足工程需求，同时也验证了本文方法的准确性。

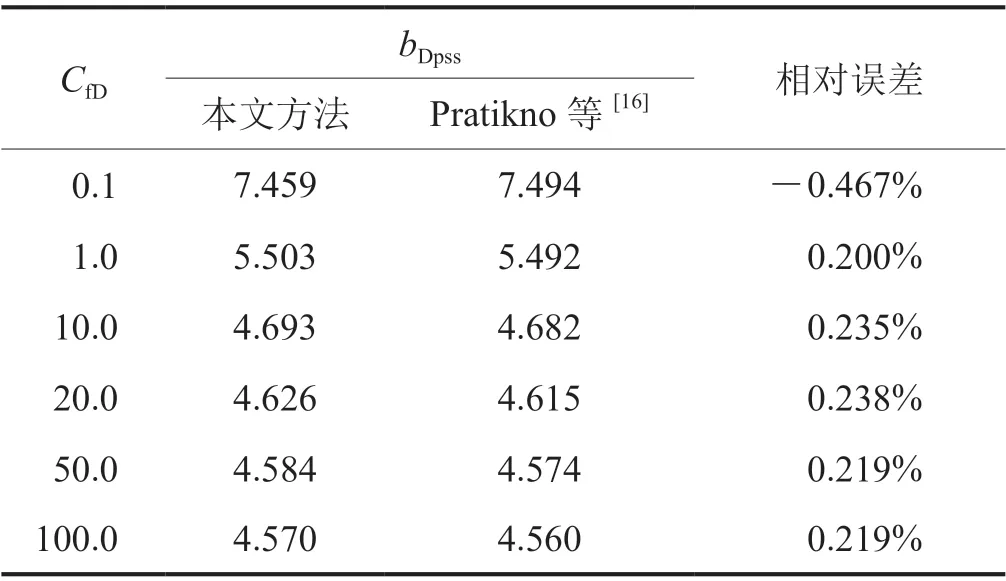
表2 圆形封闭边界油气藏有限导流压裂直井bDpss结果对比表

3.3 矩形封闭边界油气藏＋有限导流压裂直井

王晓冬等[17]推导出矩形封闭边界油藏有限导流多段压裂水平井井底压力解。之后，Xing等[18]基于圆形封闭边界油气藏有限导流压裂直井井底压力解，得到矩形封闭边界油气藏有限导流压裂直井的bDpss，其计算式为：

其中

u=lnCfD

式中xeD、yeD分别表示矩形封闭边界油气藏无因次宽度与长度；xwD、ywD分别表示压裂井所在位置无因次横、纵坐标；xD、yD分别表示计算点所在位置无因次横、纵坐标。

图6分别绘制出矩形封闭边界油气藏有限导流压裂直井（pwD－p'wDtDA）—tDA和（pwD－pwDps）—tDA曲线，可以看出，在压力波未到达封闭边界以前，（pwD－p'wDtDA）随tDA增大而增大，当压力波到达封闭边界以后，（pwD－p'wDtDA）为一定值，该数值即对应式（8）中bDpss的数值。求得bDpss，即得到了有限导流压裂直井拟稳态流动阶段井底压力渐近解。绘制（pwD－pwDps）—tDA曲线，如图6所示，在压力波未到达封闭边界之前，（pwD－pwDps）随tDA增大而减小，当压力波到达封闭边界以后，（pwDpwDps）为0，从而证实利用本文方法计算的拟稳态流动阶段井底压力渐近解（pwDps）是正确的。

再利用Xing等[18]计算的bDpss与采用本文方法计算的bDpss进行对比，发现裂缝导流能力无论如何变化，两种方法计算的bDpss相对误差都很小（表3），完全能够满足工程需求，同时也验证了本文方法的准确性。

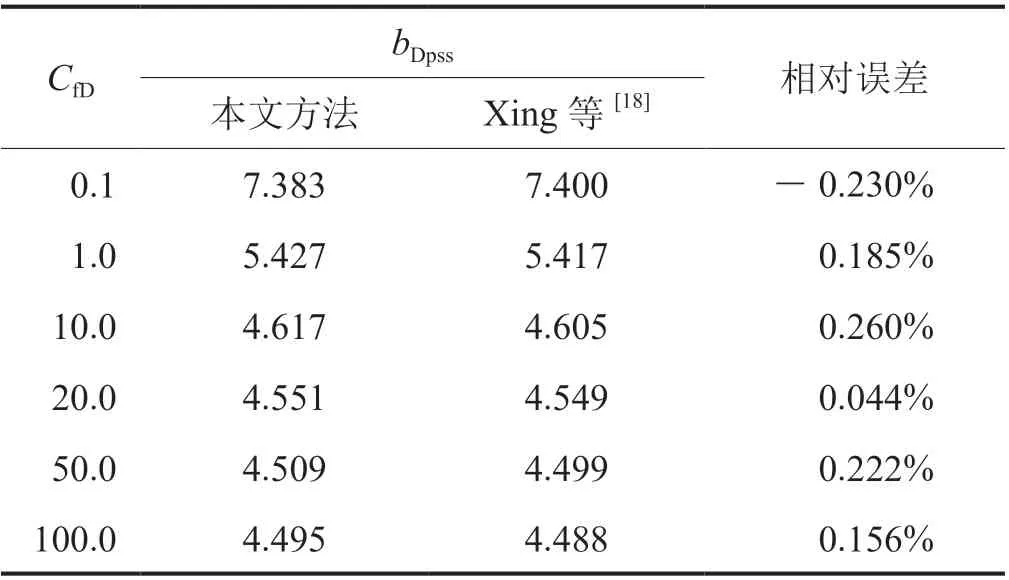
表3 矩形封闭边界油气藏有限导流压裂直井bDpss结果对比表（考虑CfD变化）

通过大量计算后发现，对于矩形封闭边界油气藏而言，长宽比不仅影响bDpss，还影响拟稳态流动阶段开始的时间。如图7所示，图中蓝色点则对应拟稳态流动阶段开始的数据点，其横坐标对应拟稳态流动阶段开始的时间，纵坐标则对应bDpss。在不同长宽比条件下，将采用本文方法计算的bDpss与Xing等[18]计算的bDpss相比，相对误差维持在0.5%左右（表4），满足工程需求，再一次验证本文方法的准确性。

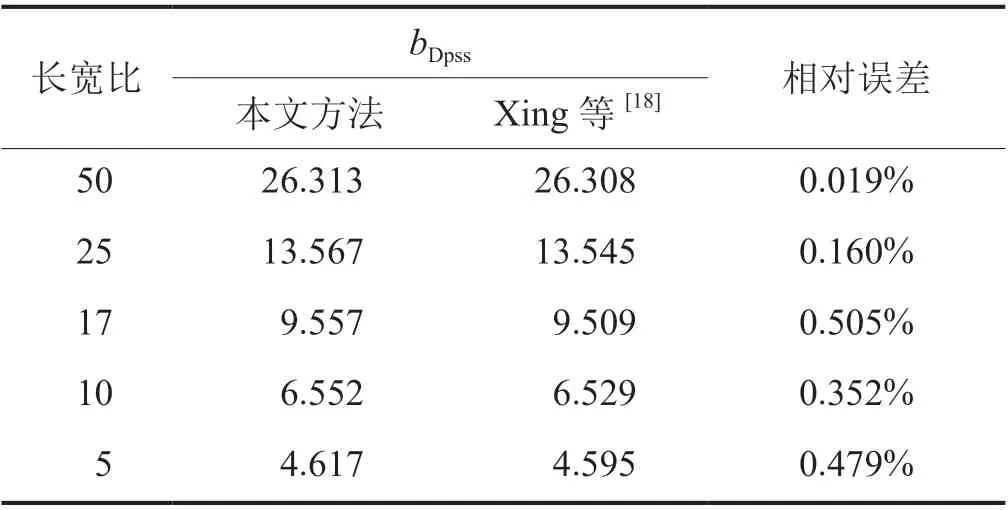
表4 矩形封闭边界油气藏有限导流压裂直井bDpss结果对比表（考虑长宽比变化）

4 Blasingame递减曲线典型图版的绘制

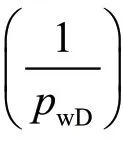
式中tDd表示Blasingame递减曲线无因次时间；qDd表示Blasingame递减曲线无因次产量。

无因次产量积分及产量积分导数曲线计算式为：

式中qDdi表示Blasingame递减曲线无因次产量积分；α表示积分变量，无量纲；qDdid表示Blasingame递减曲线无因次产量积分导数。

基于式（11）～（14），针对常规直井绘制Blasingame递减曲线典型图版，如图8所示，在拟稳态流动阶段qDd—tDd曲线呈斜率为－1的直线，并且长宽比越大，晚期线性流特征越明显。

对于压裂直井，假设该井位于油气藏中心位置，裂缝延伸方向和矩形封闭边界油气藏的长度方向一致，如图9所示，在油气藏外边界长度一定的情况下，若长宽比越大，单井控制面积越小，bDpss越大，晚期线性流特征越明显，Blasingame递减曲线在非稳态流动阶段所处的位置越高。如图10所示，在单井控制面积相同的情况下，若裂缝导流能力越高，bDpss则越小，Blasingame递减曲线在非稳态流动阶段所处的位置越高。通过Blasingame图版拟合，可以计算单井控制储量，进而确定单井控制半径[21]。

5 结论

1）针对不同形状边界油气藏直井，通过计算拟稳态流动阶段无因次井底压力（pwD）及其导数（p'wDtDA），求得两者的差值，则可以反求形状因子，并且采用本文方法计算的形状因子与Dietz形状因子结果非常接近，验证了本文方法的准确性。

2）通过求取复杂结构井拟稳态流动阶段pwD和p'wDtDA之差，则求得复杂结构井的拟稳态流动阶段井底压力渐近解系数（bDpss），进而可以获得任意复杂结构井拟稳态流动阶段井底压力渐近解。

3）基于本文方法，计算的大斜度井拟表皮因子与Ozkan等计算结果的相对误差在1%以内，验证了本文方法的准确性。

4）对于矩形封闭边界油气藏中常规直井，拟稳态流动阶段Blasingame递减曲线的无因次产量曲线斜率为－1，并且长宽比越大，晚期线性流特征越明显。

5）对于矩形封闭边界油气藏中压裂直井，在外边界长度一定的情况下，若长宽比越大，单井控制面积则越小，bDpss越大，晚期线性流特征越明显，Blasingame递减曲线在非稳态流动阶段所处的位置越高；在单井控制面积相同的情况下，若无因次裂缝导流能力越大，bDpss则越小，Blasingame递减曲线在非稳态流动阶段所处的位置越高。