海洋深水钻井隔水管气液两相流的多普勒超声波传播特征
顾纯巍 李 骞 马 睿 林英松 李相方李轶明 张爱霞 李英杰 尹邦堂
1. 中海石油(中国)有限公司 2. 中国石油西南油气田公司勘探开发研究院 3. 中国石油大学(华东)石油工程学院4. 中国石油大学(北京)石油工程学院 5. 中国石油集团海洋工程有限公司
0 引言
近年来,海洋钻井发生了多起井喷事故[1-3],带来了不可估量的经济损失和难以挽回的人员伤亡,而且对海洋生态环境也造成了巨大的破坏,其中较为严重的是墨西哥湾深水地平线钻井平台井喷事故[2-3],直接经济损失超过4 800 亿元。溢流早期监测是防止井喷失控的一个重要手段[4-7],提前发现溢流3分钟,井喷发生的可能性可以降低50%。
目前,陆上及海洋浅水所用泥浆池液面[8-10]、环空返速[11-13]等气侵监测方法发现溢流时间晚、精度低;井下随钻监测法[14-16]一方面服务成本高,另一方面高温高压地层不适用。近些年出现了声波等隔水管外进行溢流监测的研究,但是声波时差法[17-19]对于钻井液中含有较多岩屑颗粒时衰减厉害,并且平台施工对声波传播影响大。随着科技不断发展,20世纪80年代,国内外学者在时差法和频差法的基础上提出了多普勒法[20-22],从而使超声检测技术的精度进一步提升。Murakawa等[20]开发了一种多波超声波传感器用于测量垂直管道中的气泡流量与流速。Wada等[21]提出了一种利用超声回波检测气液两相流动的方法。前人在多普勒理论的基础上,通过大量实验,验证了超声波多普勒检测气液流量的可行性和正确性。但目前还未将相关理论应用于气侵早期监测,也未发现多普勒信号与含气率之间的定量表征关系。
为此,笔者首先搭建了多普勒超声波在气液两相中的传播实验装置,优化了探头安装方式及角度;开展了含气率介于0~46%、液相流速介于0~0.7 m/s的气液两相流中的多普勒超声波传播实验,揭示了停泵及开泵不同流速条件下的多普勒超声波信号随含气率的变化规律,建立了两者的定量表征关系,以期为开展溢流早期监测提供理论依据。
1 多普勒超声波的传播机理
多普勒超声波在纯液相中传播时,发射与接收到的信号频率基本相同,无差异。多普勒超声波在混合介质中传播时,随着传播距离的不断增加,能量会逐步衰减。它的衰减程度受超声波扩散、散射及吸收等因素的影响。散射衰减是指超声波在大量尺寸远小于波长的散射粒子表面形成散射,其中一部分声能传播方向发生改变的现象。在形成散射之后,诸如气泡等散射物质将变成声源,从而向所有方向辐射声能,散射衰减的强弱与散射粒子的形状、数量、尺寸、粒子性质和介质性质有关。吸收衰减是指一部分声能在通过气泡的过程中不可逆转地转换成了其他形式的能量,这意味着超声波通过介质传播时一部分能量被吸收,导致声能损失。
多普勒超声波传播过程中的频率关系表达式为:
式中f '表示观察到的频率,Hz;f表示发射源在液相中的原始发射频率,Hz;v表示波在液相中的传播速度,m/s;vo表示观察者的移动速度,m/s;如果接近发射源移动,则前面运算符号为正,反之为负;vs表示发射源移动速度,m/s;如果接近观察者移动则前面运算符号为负,反之为正。
如图1所示,液相的流动速度是u,液相中超声波的传播速度是c,发射传感器与水平面的发射角度是α,发射传感器发射的超声波频率是f1,液相中气泡接收到的超声波频率是f2,接收传感器接收到的超声波频率是f3。
当发射传感器发射的超声波以速度c遇到以速度u沿管路轴线运动的气泡,对于发射传感器,气泡正以ucosα的速度向远处移动,因此由液相中气泡接收到的超声波频率低于发射传感器发射的超声波频率,该频率为:
气泡又将超声波束散射传递到接收传感器,由于它是以ucosα的速度远离接收传感器,所以接收传感器接收到的超声波频率再一次降低,该频率为:
进一步得到:
由此,获得单个反射波的多普勒频移,即
因为,超声波在流体中的传播速度c远大于流体的速度u,所以可以省去ucosα,所以该式可以简化为:
由上述分析可知,一旦气体进入液相中,气泡表面就会对多普勒超声波形成反射,作为多普勒超声波在液相中的接收端和二次发射端,造成信号的衰减,频率发生变化。气体含量(含气率)不同,频率的变化量不同。因此,可以通过监测多普勒超声波信号的变化,来推测气体的含量。
2 实验设计
2.1 实验平台
基于上述分析,搭建了多普勒超声波实验平台,如图2-a所示。实验平台主要包括主体循环管,液体注入与排出系统,气泡发生系统及信号检测系统4个部分。主体循环管底部安装有液体流量计和气体流量计,可以分别对液体和气体的通入量进行监测。气泡发生系统主要由气体压缩机,气泡粉碎装置及数个阀门组成。空气压缩机与主体循环管的底部进行连接,经过压缩的气体从底部进入主体循环管,通过气泡粉碎装置将大气泡打碎成小气泡,然后随着液体一起上返。
信号检测装置主要包括多普勒探头,激励电源及示波器(图2-b)。发射与接收探头的正极与负极分别与激励电源相连接,接收探头的信号线与示波器连接。实验中选用的示波器定时分辨率为10 µs,即每秒可读取100 000个点。通过观察发现,示波器能够将超声波信号用电压幅值的方式清晰地表示出来。发射探头在电源的激励作用下发出正弦波,当管内流速或含气率发生改变时,示波器接收到的波形会发生相应变化。
2.2 多普勒超声波传感器安装
超声波传感器的安装方式往往决定着实验的成败,由以下几个参数来决定。
工程实际中,超声波多普勒气液两相流探测换能器有几种典型的安装方式,如图3所示,发收换能器置于管道的对侧;发收换能器置于管道的同侧;使用发收合置探头。因主体循环管内部有一个钢制的模拟钻柱,当选用对侧的安置方式时,超声波多普勒信号在钻柱表面形成反射,从而造成大量衰减。因而只能选择同侧安装的方式来布置探头。通过实验来确定双探头同侧安装的最佳角度,使接收到的信号最明显。
实验过程中,选择在停泵状态下探究双探头同侧安装的最佳角度,分别在60°、90°、120°和150°的角度下对信号的强度进行测试。通过比较不同角度下,信号在示波器上的强弱程度来确定最佳的安装角度。实验结果显示,当安装角度为120°时信号的效果最明显。
为了把检测范围覆盖到整个主体循环管的可视区域,在同一含气率情况下分别进行1发1收、1发2收和1发3收的探头安装情况进行测试,实验结果如图4所示。无论是采取1发1收、1发2收还是1发3收的方式,在同一发射探头的情况下,不同的接收探头在不同的位置接收到的信号是基本相同的。因此,本实验最终采取1发1收方式。
2.3 实验步骤
①打开示波器,已固定在管壁上的接收探头会把超声波信号传输到示波器,上面实时显示波形并将数据存储到示波器内。②开泵循环。③打开注气阀门向主体循环管内注入气体,达到所需含气率后,稳定泵速及注气速度,示波器记录数据;然后进行下一组实验。
3 实验数据分析
多普勒超声波时域信号分析时域分析是一种能够对时变非平稳信号进行分析的信号处理方法,能够对信号频率随时间的变化关系进行清晰的描述。
3.1 停泵状态下的时域信号分析
通过调节空气压缩机阀门的开度来控制进气量的大小,模拟信号电压波形在不同含气率状态下的变化情况,共计22组,含气率变化范围是0~46%。观察含气率2.4%、13.2%、22.2%和35.2%的波形发现,随着含气率增加,单位时间内信号电压的变化速率明显加快;含气率从2.4%到22.2%,信号电压幅值不断增大,而22.2%与35.2%的信号电压幅值基本相同。
进一步对含气率13.2%、16.8%、22.2%、28.1%、35.2%、39.0%、42.4%和45.6%时的信号数据进行处理,如图5所示。
由图5可知,随着含气率增加,信号电压幅值呈现增大、相对稳定、下降的变化趋势;而波形由稀疏变得细密,说明信号的变化速率不断加快。以上论述表明,当含气率发生变化,信号电压会在初始正弦曲线的基础上以不同的幅度和频率上下跳动,信号电压幅值与变化速率可以共同反应含气率的大小。
针对某一个含气率情况下0.10 s内的10 000个点,对它们绝对值化后求取平均值得到信号电压均值。做出信号电压均值随含气率的变化曲线,如图6所示。
当不通气时,超声波在管内传播时没有反射介质,大部分能量以散射的方式衰减消失,因此信号电压均值很小。从图6可以发现,随着气体进入循环管路,单位体积内气泡的数目增加,导致整体气液界面数目增加,超声波因为气体侵入导致衰减增大,同时气液界面处会发生多重反射。当含气率小于22.5%时,多重反射对信号电压均值的增幅大于超声波的衰减,信号电压均值会随着含气率的增加而增大,并在22.5%时达到最大;当含气率大于22.5%时,随着气体增多,超声波的衰减将大于多重反射的影响,并且随着含气率增加这种趋势会加剧,信号电压均值减小。接下来对含气率和信号电压均值构成的散点进行曲线拟合,结果如图6所示。
图6中曲线是根据信号电压均值的散点拟合出的趋势线,呈现一个二次函数的分布形式,函数表达式为:
在已知信号电压均值的情况下可以反推出所对应含气率的近似值。
3.2 开泵状态下的时域信号分析
开泵进行循环,保持流体速度为0.65 m/s。然后重复停泵状态下的操作,调节空气压缩机阀门开度,进行不同含气率状态下信号电压变化模拟,共计22组。表1是不同含气率条件下的进液量与进气量。
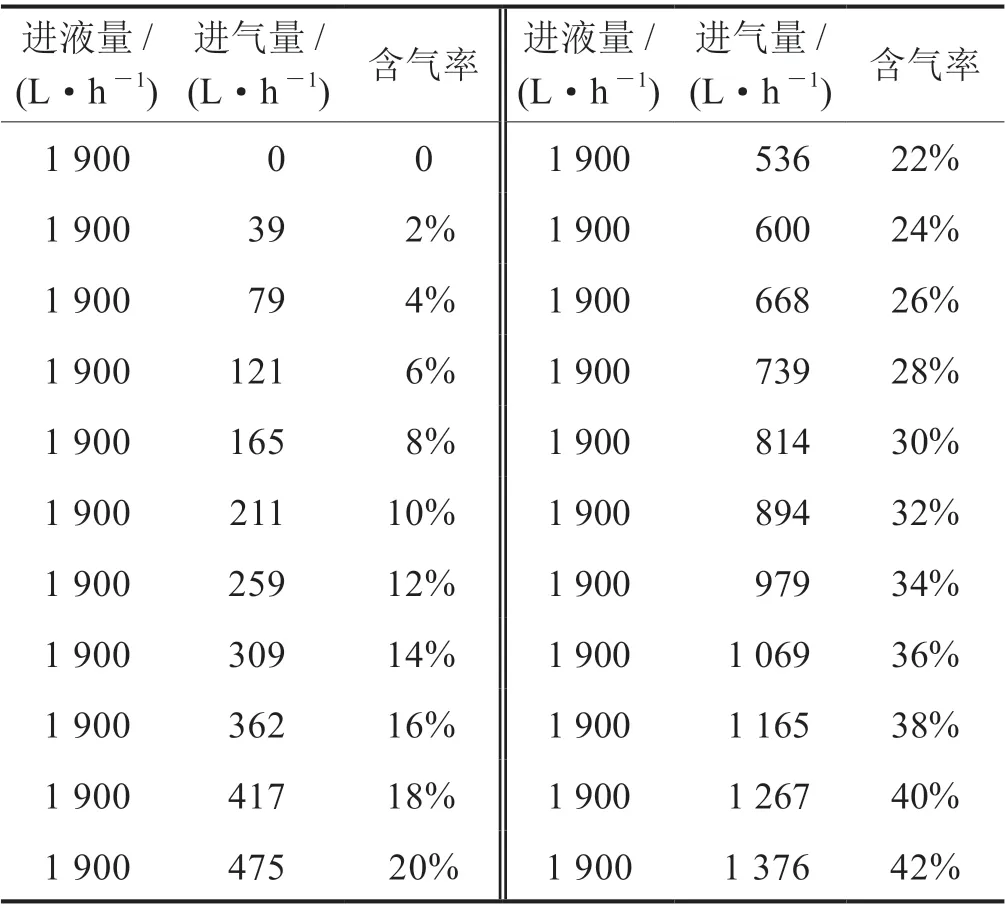
表1 不同含气率条件下的进液量与进气量表
对流速0.65 m/s条件下的实验数据进行分析,发现随着含气率增加,信号电压幅值先增大后减小。然后重复停泵条件下信号电压均值的处理方式,得到信号电压均值随含气率的变化曲线,结果如图7所示。可以发现,开泵时信号电压均值与不开泵时相比明显增大,但是变化规律基本相同,均表现为先上升后下降,峰值点出现时的含气率介于20%~25%,与停泵状态下的峰值点含气率22.5%接近。对该流速下的信号电压均值散点进行曲线拟合,结果如图7所示,拟合曲线也呈现二次函数的形式,即
使用相同方法对流速0.4 m/s条件下的多普勒信号进行处理,亦发现与流速0.65 m/s有相同的变化趋势,表达式为:
通过对式(7)~(9)进行分析整理,分别得到它们的对称轴如表2所示。

表2 拟合二次函数的对称轴表
通过观察发现上述3式都可以用同一个二次函数式来表达,该式为:
该二次函数式中,对称轴为x=0.215 ± 0.01,a和b与流速和信号电压强度有关,非定值。上式能够清晰反映信号电压均值与含气率之间的对应关系,在已知信号电压均值的条件下,可定量求取含气率。可将此方法应用于深水钻井隔水管外气侵早期监测(图8)。
如图8所示,将多普勒发射、接收传感器安装于隔水管外,由发射传感器发射多普勒信号,经钻井液后,由接收传感器接收信号,将返回的信号传输至平台处理系统,与发射信号进行对比,如果没有发生变化,则无气侵发生;如果信号电压均值发生变化,则根据建立的关系式定量表征出含气率。
4 结论
1)设计并搭建了多普勒超声波在气液两相流中传播的实验装置,优化了探头安装方式,采用一发一收及同侧夹角120°安装方式,信号效果最优。
2)开展了含气率介于0~46%、液相流速介于0~0.7 m/s条件下多普勒超声波传播实验,发现:气泡对超声波形成反射,信号电压的幅值随之变化;随着含气率增加,信号电压幅值呈现增大、保持相对稳定,最后下降的变化趋势。
3)含气率与信号电压均值散点拟合曲线基本上呈现一个二次函数的形式,y=a[x- ( 0.215±0.01 )]2+b,在已知信号电压均值的条件下,可定量表征出含气率的大小,从而指导溢流早期监测及压井作业。

