培养中学生良好数感的实践策略研究

袁国虎

摘  要：隨着中学数学综合性和复杂性的不断增加，学生需要养成良好的数学观察习惯，重视常见公式之间的基本结构特征，寻找几何图形中隐藏的内在特殊规律，尝试各种假设、变式训练，洞察解题规律和本质，找到巧解、妙解、化繁为简的解题途径。

关键词：数学观察;基本结构;特殊规律;解题技巧;变式训练

中学阶段，数学概念不断扩充，数学题的综合性和复杂性增加，有些学生开始采用题海战术，但是实践证明，在考试中往往原创题居多，学生仍然一筹莫展。“减负”应该减去哪些不利于学生健康成长的高消耗、低产出的过重负担？在数学教学中，教师应该如何培养学生面对这些原创题？针对如何培养学生良好的数感，具体结合初中数学教学实践探究如下。

一、在观察中让学生找到解题突破口

观察要从问题入手，问题是数学的心脏。数学观察包括观察数式内在的关系和图形中隐含的规律。几何问题尤为重要，其中一些看似平淡无奇的信息，通过有效观察找到关键信息，挖掘出其中隐含的有价值的信息，解题思路会豁然开朗，清晰明了，避繁就简。

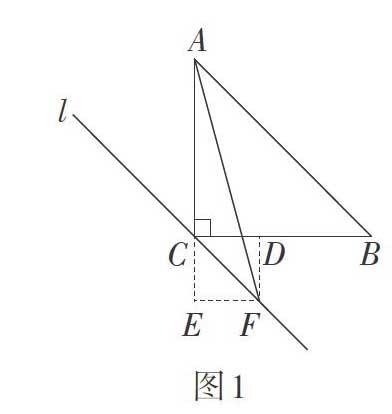
例1  在等腰直角三角形ABC中，∠C = 90°，AC = 1，过点C作直线l∥AB，F是l上的一点，且AB = AF，求点F到直线BC的距离。

思路1：如图1，当点F在点C右侧时，得四边

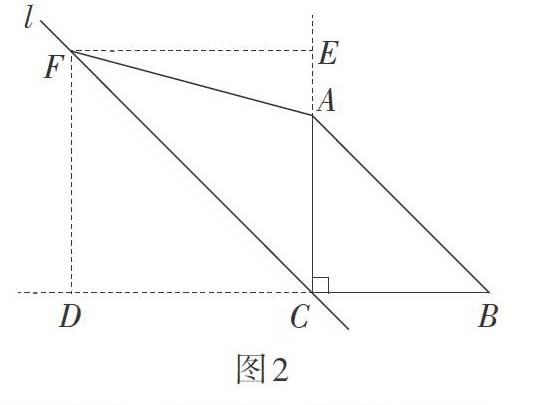
形CDFE是正方形，得[DF=3-12。] 如图2，当点F在点C左侧时，得四边形EFDC是正方形，得[DF=3+12。]

思路2：从条件AB = AF出发，如图1，发现∠FAB = 30°，设EF = CE = x，则BD = [3x。] 根据BD+ CD = BC，得[3x+x=1，] 解得[x=][3-12，] 即[DF=3-12。]同理，如图2，可求得[DF=][3+12。]

二、引导学生从数和式的结构中提升数感敏锐性

数和式之间的基本结构通常是指基本的公式、方程、不等式和函数的结构特征。先熟悉公式am·an·ap = am + n + p，[amnp=amnp， abn=anbn，am÷an÷ap=]am - n - p，其中m，n，p都是正整数，a ≠ 0;常见代数式乘法公式，如[a+ba-b=a2-b2， a±b2=a2±2ab+b2，x2+][px+q=x+ax+b;ax2+bx+c=ax-x1x-x2。] 另外，还要熟悉[ax2+bx+c=0 a≠0]中的[x1+x2=-ba，x1x2=ca，]以及常见的变形公式[x1-x2=x1+x22-4x1x2]等。

例2  解二元二次方程组[xy=6 ①，x+y=5 ②。]

解析：设x，y是方程z2 - 5z + 6 = 0 ③的两个根，由方程③解得z1 = 2，z2 = 3，所以原方程组的解为[x1=2，y1=3，] [x2=3，y2=2。]

三、从图形结构中诱发猜想，提高思维广度

基本图形结构通常指几何中的基本图形。抓住基本图形的隐含条件，养成有意识地由特殊情形诱发猜想的习惯，能提高学生思维的广度。

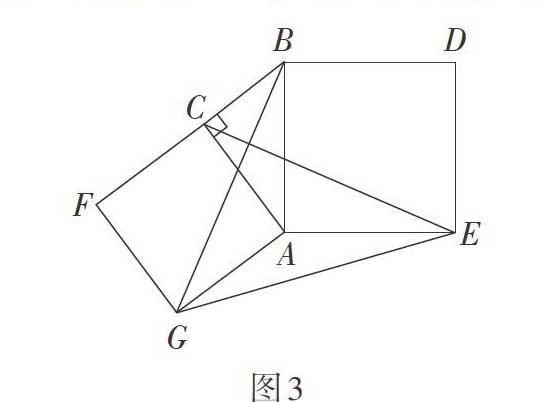
例3  如图3，分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE，连接CE，BG，GE。已知AC = 4，AB = 5，求GE的长。

解析：由题可知，对角线相互垂直的四边形CGEB尤为关键。通过探究发现“对角线相互垂直的四边形的两组对边的平方和相等”这一规律是解题的突破口。

四、在变式中洞察数学规律，提高数学思维品质

变式训练如何变，就是将母题进行变化，尝试从概念、背景、条件与结论、题目的形式、难易程度复杂性、涉及知识点的综合性等方面和角度加以变化，如利用完全平方公式[a±b2=a2±2ab+b2]衍生的常考题型“整体代入法求代数式的值”。

例4  已知[x+][1x=6，] 求[x-1x]的值。

变式1：已知[x-1x=6，] 求[x+1x]的值。

变式2：已知[x+1x=2，] 求[x2+1x2+14]的值。

变式3：已知[x+1x=3，] 求[xx2+1]的值。

变式4：已知x2 - x - 1 = 0，求[x-1x]的值。

变式4解析：因为[x≠0，] 将分式[x-1x=1]两边同时乘以x，得一元二次方程x2 - x - 1 = 0，找到巧解一元二次方程与分式的关系。

总之，学生有了良好的数感之后，让学生自己去探索、解析、综合，以提高学生解数学题的速度，最终达到数学建模的目的。无论将原创题怎么变化，学生都会快速发现解题的突破口，即使找不到解题入口，也会套用数学建模思路去解析探究，直至解决。

参考文献：

[1]李果民. 中学数学教学建模[M]. 南宁：广西教育出版社，2003.

[3]张仁贵，严虹焰. 教师如何进行学法指导[M].天津：天津教育出版社，2009.