缸内燃烧过程中缸盖表面振动信号分析与研究

王 洋， 程 勇

(山东大学 能源与动力工程学院，济南 250061)

许多研究者采用了诸如基于相干性分析的滤波技术[1-2]，以及经验模态分解[3-4]、神经网络[5-6]和盲源分离[7-8]等信号处理方法，从内燃机缸盖表面振动信号中获取与燃烧过程相关的信息。

基于相干性分析的滤波技术通过相干性分析选择合适的频率窗，认为窗口内的振动响应与燃烧过程高度相关，并从中提取燃烧过程特征参数，如燃烧始点等。但此方法获取的与燃烧过程特征信号间的对应关系往往是人为确定的，且测试用发动机机型及工况不同时，频率窗的选择不同，特征参数的对应关系也不同。因此，有必要进一步指出此对应关系变化的原因。

经验模态分解(empirical mode decomposition, EMD)是一种自适应信号处理方法，可以直接或结合盲源分离技术从缸盖表面振动信号中提取某些信息。但EMD算法存在模态混叠问题，分解出的本征模函数的激励源组成尚需进一步揭示，否则难以保证获取的燃烧激励响应信号的完整性和有效性。

鉴于此，考虑到缸内燃烧信息的提取往往需要以各个激励源作用下缸盖表面振动响应间耦合关系作为分析基础，以激励源相对较少的单缸柴油机为研究对象，基于台架试验与仿真分析，对采用带通滤波技术和EMD算法从振动加速度信号中所提取信息的完整性及有效性进行了讨论，利用修正后的EMD算法对燃烧始点进行了识别。

1 单缸机缸盖振动信号的测取

试验用柴油机型号为SD195，缸径95 mm，行程115 mm，排量0.815 L，额定转速2 000 r/min，额定功率8.8 kW，进气门早开、晚关角为17、43 °CA，排气门早开、晚关角为43、17 °CA，供油提前角为18～22 °CA。主要测试设备为：加速度传感器型号CA-YD-102，轴向灵敏度15 pC/g，量程5 000g，磁座安装方式下的频率响应为2～5 kHz；压电式压力传感器型号12QP250，量程15 MPa，灵敏度200 pC/MPa；电荷放大器型号YE5850A、YE5852，灵敏度0.01～1 000 mV/pC；数据采集卡型号MP426，14位AD精度。加速度传感器利用高强度磁铁吸附于缸盖表面，用于测取气缸轴线方向的振动加速度信号；曲轴转角信号和曲轴位置信号由两个磁电式传感器测取。各信号以每通道50 kHz的采样频率同步采集。加速度信号和缸压信号参照采集的曲轴转角信号和曲轴位置信号由时间域转到曲轴转角域[9]。图1(a)、(b)分别显示了1 000 r/min-10 N·m，1 400 r/min-10 N·m工况下实测的振动加速度曲线、缸内压力曲线和计算得到的缸内压力二次导数曲线，其中EVC、IVC、FSAG、EVO及IVO分别表示排气门关、进气门关、供油提前角、排气门开及进气门开的角度。

(a) 1 000 r/min-10 N·m

2 虚拟样机模型的建立及结果分析

分离出缸盖-机体部件，基于ADAMS软件建立了试验用单缸机的虚拟样机仿真模型[10]，如图2所示。模型中用4个衬套部件模拟发动机的支撑，用4个弹簧部件模拟缸盖螺栓。衬套部件的刚度和阻尼由力锤试验进行标定，进行力锤试验时发动机的约束状态及加速度的测点与台架试验时一致；弹簧部件的刚度由缸盖螺栓的连接刚度换算得到。

图2 虚拟样机仿真模型

由单缸发动机的受力分析可知，引起缸盖表面振动的激励源主要包括缸内压力，一阶往复惯性力，二阶往复惯性力，旋转惯性力，活塞侧压力引起的摩擦力和倾覆力矩。试验用发动机往复惯性力的平衡方式为转移平衡，即将部分气缸轴线方向的一阶往复惯性力转移到垂直于气缸轴线方向，这里称为转移平衡力；旋转惯性力一般在曲轴动平衡中做了良好平衡。仿真中施加的激励源为缸内压力P，残余一阶往复惯性力Pj1，二阶往复惯性力Pj2，转移平衡力Ftr，倾覆力矩M和活塞侧压力引起的摩擦力Ff[11]。将前述所有非燃烧激励及缸内压力(下文称之为“全激励”)同时施加到模型上得到的振动加速度响信号记为Aa；将Pj1和Pj2同时施加到模型上得到振动加速度响应信号记为Apj；将Ftr、M和Ff同时施加到模型上得到振动加速度响应信号记为Ap2。

以1 200 r/min-10 N·m工况为例，将前述各个激励信号施加在模型上，得到的仿真结果如图3所示。由图3可见，仿真得到的振动加速度信号与实测的振动加速度信号在整体趋势上吻合良好。低频成分在幅值和相位上与实测结果基本一致,在非燃烧过程对应转角范围内二者的相关系数为0.82；在燃烧过程对应的转角范围内存在一定差异，认为是模型将缸盖和机体视为刚体，其刚度与阻尼与实际发动机存在一定差异所致。结合以上分析，认为施加的激励信号已经覆盖主要的激励源，对非燃烧激励响应信号描述也是合理的，仿真结果可以用于后续分析。

图3 仿真结果与实测结果对比

3 各激励振动响应信号的耦合关系及其分离技术讨论

3.1 各激励振动响应信号之间的耦合关系分析

为了分析各激励响应信号的耦合关系，对各激励源单独作用下的振动过程进行了仿真，结果如图4所示，其中Ap为缸压单独作用时仿真得到的振动加速度信号。由图可见，转移平衡力、倾覆力矩和摩擦力对应的响应信号的最大幅值约为缸压激励和惯性力激励响应信号幅值的5%。缸压和惯性力激励响应信号的均方根值与全激励响应均方值之比为0.977。分析认为，转移平衡力的作用方向与测取的振动加速度方向垂直；倾覆力矩引起的卧式发动机绕曲轴旋转中心的“摆动”在振动加速度的测取方向上的贡献很小；摩擦力虽与测取加速度的方向一致，但幅值相对较低，也未对缸盖表面振动加速度信号做出大的贡献。这三种激励对活塞运动方向振动加速度信号的影响可以忽略，即在燃烧激励作用阶段，测取的缸盖表面振动加速度信号相应的激励源主要是缸内压力和往复惯性力。

(a) 各激励源贡献度分析

图5为1 200 r/min-10 N·m工况下缸内压力，缸压二阶导数及缸压激励振动加速度响应信号的时频变换结果。由图可见，缸压的频带分布在0～2 kHz，其主要能量分布在0.25 kHz以下，并且持续在整个发动机循环；缸压二阶导数频带分布在0～2 kHz，其能量主要分布在在0.4～1.5 kHz；缸压激励振动加速度信号的频带及能量分布与缸压二阶导数的基本一致，其能量主要分布在0.5～1.5 kHz，在0.5 kHz以下的能量相对较少。图6为全激励作用下的仿真振动加速度信号的时频变换结果。相对图5(c)，图6在40 Hz左右出现了持续于整个发动机循环的能量带，由于仿真分析中忽略了发动机瞬时转速的波动，在1 200 r/min时二阶往复惯性力的频率为40 Hz，故此成分的激励源主要是往复惯性力。可见，往复惯性力激励响应与缸压激励振动加速度响应的低频部分存在重叠，因此采用带通滤波器提取与缸压二阶导数对应的振动加速度信号，能量的损失取决于影响缸压二阶导数的缸内燃烧过程的剧烈程度以及影响往复惯性力频带的发动机转速，即发动机的工况不同，带通滤波引起的与缸压二阶导数对应的振动加速度信号的损失不同。

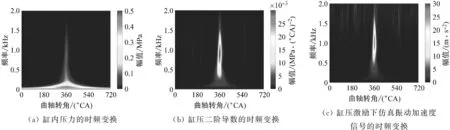
图5 缸压、缸压二阶导数及其响应的时频变换

图6 全激励下仿真振动加速度信号的时频变换

3.2 燃烧激励振动响应信号分离技术讨论

3.2.1 基于相干性分析的滤波技术讨论

参考文献[2]建议的带通滤波器频带设置方法，通过相干性分析选取的带通滤波器频带范围为0.5～1 kHz，对实测振动加速度信号进行了滤波处理。图7(a)显示了滤波结果与缸压二阶导数的对比。由图可见，带通滤波后的振动加速度信号与缸压二阶导数在350～375 °CA范围内具有相似的变化趋势。根据内燃机工作过程分析，认为缸压二阶导数峰值点之前的第一个过零点对应燃烧始点，结合图7(a)所示的对应关系，可用与之对应的振动加速度峰值点之前的第一个极小值点表征燃烧始点，并用振动加速度峰值点之后的第一个极小值点近似表示缸内峰值压力出现位置。

(a) 单缸机的对比结果

为了验证此对应关系的普适性，在4缸机上测取了缸内压力和缸盖表面振动加速度信号，经相干性分析确定的带通滤波器频率范围为0.4～1 kHz，并据此对振动加速度信号进行了滤波处理。图7(b)显示了带通滤波后振动加速度曲线与缸压二阶导数的对比。可见，带通滤波后的振动加速度曲线与缸压二阶导数存在一定差异，并且特征点的对应关系出现变动。

以上结果可见，尽管基于相干性分析的带通滤波技术可以获取与燃烧过程高度相关的振动加速度曲线，但曲线上的特征点与燃烧过程特征参数的对应关系不具有普适性。由前述仿真分析结果及图5、6可知，由于缸压激励与往复惯性力激励存在频带重叠，对振动加速度信号的带通滤波处理在滤除往复惯性力激励响应信号的同时，会导致与缸压二阶导数对应的振动加速度信号的损失，且发动机机型及缸内燃烧状态不同时，基于相干性分析获取的频率窗范围不同，致使提取的与缸压二阶导数对应的振动加速度的能量损失不同，这影响到滤波后的振动加速度曲线与缸压二阶导数曲线的对应关系。

3.2.2 EMD算法的讨论

EMD也是一种常用的从发动机表面振动信号中提取燃烧过程有效信息的方法。为进一步分析EMD算法得到的本征模函数(intrinsic mode function，IMF)的激励源组成，对1 200 r/min-10 N·m工况的实测振动加速度信号进行了EMD分解，得到了10个IMF，如图8所示。由图可见，前4阶IMF频带相对较高，在燃烧过程对应的曲轴转角范围有较多的能量分布；余下的IMF频带相对较低，分布在整个工作循环中，但在燃烧区域没有反映出更多的信息。

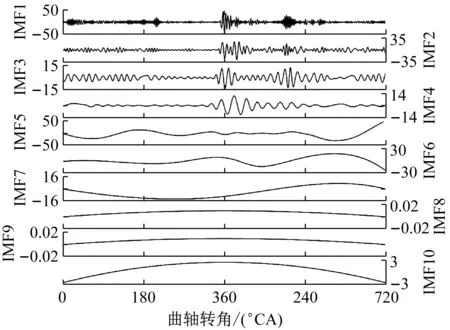
图8 实测加速度信号的EMD分解结果

由于前4阶IMF分量主要集中在燃烧过程对应的转角范围，对其作求和处理，结果如图9所示。由图9可见，前4阶IMF分量之和(记为AIMF1-4)与缸压激励仿真振动加速度曲线在关注的350～375 °CA转角范围具有近似的变化趋势，对其进行了时频变换，结果如图9(b)所示。由图可见，其能量主要分布在0.4～1.5 kHz，与缸压二阶导数相对应，因此可认为前4阶IMF分量之和代表了与缸压二阶导数对应的振动加速度信号。

(a) 缸压二次导数曲线、前4阶IMF分量之和曲线与缸压单独作用下的振动加速度曲线的对比

剩余低频IMF分量均分布于整个发动机循环，对其做求和处理(记为AR)后发现与往复惯性力作用下的仿真振动加速度的整体变化规律基本一致，如图10所示。二者相关系数为0.83，可认为余下分量的激励源主要是往复惯性力。

图10 低频IMF之和曲线与往复惯性力激励仿真振动加速度曲线的对比

signals

由图10可看到，AR在压缩上止点附近出现一个波动，此波动显然与往复惯性力激励无关，应属于燃烧激励响应信号。这是由于与缸压二阶导数对应的振动加速度信号的高频部分集中在上止点附近一小段曲轴转角范围，使得EMD算法产生模态混叠问题，即燃烧激励响应与往复惯性力激励响应并未完全分离所致。

(1)

式中，B1，B2，β1，β2均为与发动机结构及转速相关的常数，可通过与AR的对比得到。

(2)

(3)

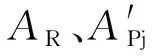
图11 相继循环下识别的特征点

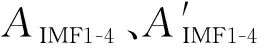
图12 燃烧激励响应信号的修正

为了考核修正方法的有效性，以1 200 r/min-40 N·m工况的测试结果为例，统计了连续80个循环的φSOC、φ1及φ2，结果见图11。其中，φ1、φ2标准差分别为1.910、0.367，可见根据修正后燃烧激励响应曲线得到的特征点更加稳定。

对800 r/min、1 000 r/min-10 N·m 、1 200 r/min-10 N·m、1 200 r/min-50 N·m、1 400 r/min-10 N·m和1 400 r/min-50 N·m六个工况、每个工况80个循环的数据进行了统计。图13分别显示了统计得到的φ1、φ2与φSOC偏差的分布图。修正前后滞后角度的标准差分别为1.355和0.476。经过修正，振动加速度曲线上与燃烧始点对应的特征点间的离散程度明显降低。

(a) 修正前的滞后角度

由此可见，由于与缸压二阶导数对应的高频振动加速度信号的时间分布范围很窄，使EMD分解的燃烧激励响应与非燃烧激励响应间存在模态混叠问题。对EMD分解得到的燃烧激励响应进行修正有利于改善模态混叠问题，降低提取的燃烧激励响应信号曲线上特征点的离散度。此方法在多缸机上的适用性将在今后的工作中开展。

4 结 论

(1) 仿真分析表明，缸盖表面振动加速度信号的激励源主要是缸内压力和往复惯性力；二者振动响应信号的频带存在重叠，重叠部分的能量取决于发动机的工况。

(2) 发动机机型和缸内燃烧状态会影响非燃烧激励响应与燃烧激励响应的频带分布，进而影响基于相干性分析的带通滤波技术的截止频率选择，使提取的振动加速度曲线上的特征点与燃烧过程特征参数的对应关系出现偏差。

(3) EMD分解得到的燃烧激励响应与非燃烧激励响应信号间存在模态混叠，利用建立的往复惯性力激励响应信号描述模型对燃烧激励响应信号进行修正，使燃烧激励响应曲线上与燃烧始点对应的特征点的滞后角离散度由1.355降低为0.476。