深度卷积神经网络在混沌振动识别中的应用研究

唐宇思， 王伟豪， 崔汉国， 刘树勇， 柴 凯

(1.海军工程大学 动力工程学院，武汉 430033； 2.海军工程大学 舰船与海洋学院，武汉 430033)

混沌振动信号快速识别是混沌应用的关键问题，国内外学者开展了深入研究。Robinson[1]利用Poincaré截面将复杂的动力系统转化到低维的空间中进行研究，从而深入、直观地展示了系统全局动力学特点；Mcdonough等[2]提出了周期轨道检测法，其主要思想是通过统计吸引子中的短周期轨道重复的时长来识别混沌信号，但该方法容易受到噪声影响；廖明等[3]通过计算功率谱是否具有1/f特征来判断时间序列是否混沌；任辉等[4]研究了学习向量量化(learning vector quantization,LVQ)对Jeffcott转子碰摩模型的非线性混沌时间序列的分类能力，实现了对这类混沌信号和其它响应信号数据的聚类，为非线性信号分类识别提供了一种方法；江亚东等[5]在对混沌时间序列与随机序列的不同特征进行分析的基础上，给出了一种基于小波神经网络的混沌时间序列判定-预测算法；Xie等[6]应用辛几何谱方法对非线性时间序列中的确定性机制进行识别，该方法比传统的奇异值分解(singular value decomposition, SVD)法更能揭示信号的本质特征；席剑辉等[7]运用扩展卡尔曼滤波算法的跟踪辨识特性，实现了对混沌系统主动态方程的参数识别和多变量混沌序列的精确预测。

然而在信号的实时识别过程中，上述方法都存在计算量大、耗费时间长等问题，特别是在舰艇辐射水声混沌谱控制过程中，由于系统工况变化，需要实时调整混沌参数、控制区域时，传统方法不能为在线调整提供快速识别。近年来兴起的深度卷积神经网络(deep convolutional neural network，DCNN)模型在图像识别领域获得巨大成功，引起人们的极大关注[8]。因分类准确率高、响应速度快，DCNN同样适用于振动信号的识别。基于以上原因，本文设计了一种针对振动信号分类的DCNN模型，可实现混沌信号的快速识别。

1 DCNN模型设计

1.1 DCNN结构分析

Fukushima[9]首次将互相关运算引入神经网络，开启了利用卷积神经网络处理图像的新纪元。典型的DCNN结构如图1所示。其构建了多个能够提取输入数据特征的卷积层，通过共享权重和空间下采样来获得输入数据平移及缩放不变的特征表示，最后利用多层全连接神经网络对特征分类，输出分类结果。

图1 典型的DCNN结构

(1)

在卷积运算前，为了保证每次运算后卷积层的宽度不至于缩减过小，对输入数据的前后做补全(pad)运算。同时为了用较少的权重元素来感知较大坐标范围的输入，对卷积核进行膨胀(dilate)。设输入数据每行前补全Pr个元素，每列前补全Pc个元素，采样步幅(stride)为S，膨胀系数为d，式(1)改进为

(2)

其中，当X的下标小于1或大于其自身尺寸时，表示补全的元素。为了便于计算，将输入数据添加一个数值全为1的通道，从而用这一通道的权值矩阵表示偏置B。因此，式(2)进一步优化为

(3)

为了引入非线性特征，在卷积运算后，将每个元素输入一个非线性的激活函数，激活后的值作为卷积层的输出。常用的激活函数为整流线性单元(rectified linear units, ReLU)，其数学表达式为

f(x)=max{0,x}

(4)

为了使用某一位置相邻输出的总体统计特征来代替网络在该位置的输出，设置了池化(pooling)操作。常用函数为最大池化函数，即给出相邻矩形区域内的最大值，其数学表达式为

(5)

DCNN应用多个卷积层完成对输入数据的特征提取，然后利用全连接层(fully connected layer)对特征进行分类。全连接层中的每一级运算可表示为

z=g(wTx+b)

(6)

(7)

式中，i=0,1,…,n，n为分类数量。

1.2 混沌振动信号识别DCNN模型

由于DCNN在直接用于处理一维的振动信号时，不仅需要确定时间序列的采样点数，还要通过加大卷积核的尺寸来获得序列前后的关联特征，将导致网络收敛过慢和过拟合问题。因此，本文通过对二维混沌吸引子的特征提取来识别信号。首先通过相空间重构(phase space reconstruction)[10]获得振动信号的相空间吸引子，再利用DCNN对信号的吸引子图分类，不仅有利于DCNN的建模，还能清晰地突显故障状态下的系统动力学特征，从而提高模型分类的准确率。

对于时间序列x，在坐标系pOq中，使用延迟重构法得到的吸引子图，可以表示为一组直线段方程

(8)

式中,τ为延迟时间。为了满足卷积神经网络的输入要求，需要将吸引子图映射到一个大小为W×H的二维像素图，表示为张量A，即对矢量图形做栅格化(rasterization)处理。计算图形的横向采样序列r和纵向采样序列c，以r为例

(9)

(10)

若kn>1或xn-xn+1=0，则将变量r和c,w和h位置互换，重复上述计算。最终得到输入卷积模型的数据

(11)

卷积层和全连接层的设计参照AlexNet[11]的结构参数，并加入dropout层[12]来防止过拟合。考虑到识别吸引子图时，不存在物体与背景的边缘识别问题，因此减小前两层的通道数以获得更好的性能。全连接层的分类识别中，由于本文需要实现的振动信号分类数量远小于AlexNet设计的分类数量(1 000)，因此逐层减小神经元数量，从而减少特征冗余并防止过拟合。

根据以上阐述，设计模型结构如图2所示。

图2 模型结构示意图

1.3 权值优化方法

DCNN中各个神经元的权重系数不能直接求得准确解，本文通过标签数据对模型的训练得到最优值，并利用批量梯度下降法训练模型。

(12)

利用Adam(adaptive moment estimation)算法[13]来更新网络参数，即权重和偏置。其本质是梯度随机目标函数优化算法，通过基于低阶矩的自适应估计，从而自适应调整学习率，可达到良好的训练效果。

2 仿真研究

2.1 仿真信号设计

设计如下不同的仿真信号

y1=sin 15πt

(13)

(14)

y3=(1+sin πt)·sin 25πt-1

(15)

τ≤t<τ+1

(16)

(17)

式中，t≥0，τ∈(N)。对上述5个信号进行采样，采样频率为1 kHz，采样点数为10 000，得到时间序列xi，(i=1,2,3,4,5)。对混沌信号，采用Lorenz系统

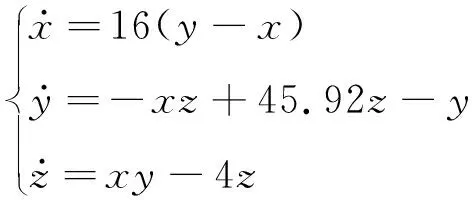
(18)

应用Runge-Kutta法求解式(18)，步长为0.01，舍去前3 000个点，取x分量的10 000个离散值作为序列x6。得到的6组仿真信号如图3所示。

图3 仿真信号时域图

应用第一最小互信息法[14]求延迟时间，重构仿真信号的相平面吸引子图，如图4所示。

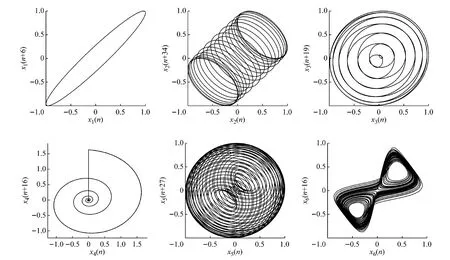
图4 仿真信号的吸引子图

2.2 生成数据集

为了提高分类模型的鲁棒性，在原信号中叠加噪声信号，生成多个数据样本。具体步骤为：

步骤1选取采样信号的第2 001～4 000点作为初始样本。

步骤2针对每个样本，随机生成100个均值为0，方差为s(0≤s≤S)的高斯噪声序列

(10)

式中:E(x2)为样本序列的均方值;RSN为信噪比(signal noise ratio,SNR)，这里设RSN=20。将这些噪声序列叠加到样本中，共得到600个不同的含噪样本。

步骤3将600个样本按照14∶3∶3的比例随机划分为训练集，验证集和测试集，得到的数据集如表1所示。

表1 仿真信号数据集

2.3 训练模型与结果分析

模型训练的参数设置如下。学习率(learning rate)：0.000 1；批尺寸(batch size)：420，即全数据集输入；迭代次数(epoch)：80。每迭代一次后，更新模型参数，计算模型在测试集上的损失值和准确率，以及模型在验证集上的准确率。训练过程中，模型的训练损失、训练准确率和测试准确率如图5所示。

(a) 损失函数随迭代次数增加而逐渐下降

由图5可知:损失函数随迭代次数的增加而减小，经过80次迭代之后，最终趋近于0；训练集和验证集的分类准确率随迭代次数增加波动上升，在迭代次数超过60次后，稳定收敛到100%。用测试集中的样本检验训练后的模型，分类准确率如表2所示。

表2 仿真信号分类准确率

不难看出，本文所提模型对6类仿真信号均能准确识别。

3 试验研究

本文采用双势阱单端磁吸式混沌振动装置[15]生成多种振动信号，试验装置原理图如图6所示。该装置通过调节激励幅值和激励频率，能够观察到系统中出现的次谐波现象、超谐波现象以及系统中周期1运动的不同模式，并能在一定频率和激励幅值条件下产生持续稳定的混沌振动。

图6 双势阱单端磁吸式混沌振动装置结构图

3.1 试验数据

前期试验发现，激振系统增益大于0.95时，系统的动力学行为非常丰富，可以产生包括混沌振动在内的不同模式。本节试验将激振系统的增益固定为 1，由小到大增加系统的激励频率，得到20组试验信号，其中混沌信号10组，非混沌信号10组，采样频率为2 kHz，采样时长为5 s。部分信号及其吸引子图如图7所示。

图7 部分试验信号时域图及吸引子图

3.2 生成数据集

为了得到更多的数据样本，对采集到的信号作数据增强处理后，再划分数据集。具体步骤为：

步骤1选取试验信号采样点的[(i-1)·S+1,(i-1)·S+L]段作为数据样本，这里令S=600，L=3 200，共获得80个信号样本。

步骤3将这1 560个样本按照14∶3∶3的比例随机划分为训练集、验证集和测试集，得到的数据集如表3所示。

表3 试验信号数据集

3.3 模型训练与结果分析

模型训练参数为：学习率：0.000 05；批尺寸：546；迭代次数：200。由于数据集尺寸过大，每一次迭代数据需要分两批依次训练，每批数据训练完后更新模型参数，每迭代一次后，计算模型在测试集上的损失值和准确率，以及模型在验证集上的准确率。训练过程中，模型的训练损失、训练准确率和测试准确率如图8所示。

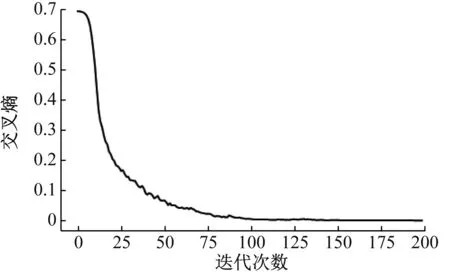
(a) 损失函数随迭代次数增加而逐渐下降

由图8可知，损失函数随迭代次数的增加而减小，经过200次迭代之后，最终趋近于0；训练集和验证集的分类准确率随迭代次数增加波动上升，在迭代次数超过150次后，测试准确率稳定收敛到100%，验证准确率在98.72%和99.15%之间波动。用测试集中的样本检验训练后的模型，分类准确率如表4所示。

表4 试验信号分类准确率

试验表明，本文所提模型能够快速准确识别混沌信号。

4 结 论

(1) 针对混沌振动信号识别中传统方法难以快速识别的问题，提出了一种基于相空间重构和深度卷积神经网络的智能识别方法。针对卷积神经网络对二维图像识别能力强的特点，利用时间延迟法将振动信号映射到二维像素图中，随后基于AlexNet设计DCNN模型对得到的像素图进行分类识别。与传统的计算混沌特征指数的方法相比，所提方法计算量小、识别速度快，可有效地应用于混沌信号的实时识别。

(2) 通过试验数据测试，所提方法能达到98%以上的识别准确率，响应快、实时性好。因此，在工程实际中具有极强的潜在应用价值。