考虑风攻角的硬跳线气动力系数和风偏计算
沈国辉, 张帅光, 楼文娟, 王轶文, 宋 刚
(1.浙江大学 结构工程研究所,杭州 310058; 2.浙江省电力设计院,杭州 310007)
在特高压输电线路中,大量使用了连接耐张塔两侧导线线夹的跳线体系。事故调查显示[1-2],跳线风偏引起的故障在所有风偏事故中占很大比重,同时发现硬跳线对风偏角的抑制效果较好,事故调查提出将硬跳线作为防跳线风偏的一个举措。研究表明[3-4],硬跳线在台风作用下也有很好的防风偏效果。鉴于其优良的抗风偏特性,硬跳线将会在输电线路中越来越广泛地得到应用。
以往跳线风偏主要的研究对象是软跳线体系(耐张夹之间直接采用导线相连),徐海巍等[5]研究微地形下软跳线的风偏计算模型和计算结果;Shen等[6]研究某软跳线体系的风偏角和三维山体风场对风偏的影响。软跳线体系的组件只有输电线和绝缘子,因此其风荷载可按照规范中导线和绝缘子的规定取值。但对于含有硬跳线的跳线体系,关于绝缘子体型系数[7-8]和多分裂导线体型系数[9-11]的结果,不能作为硬跳线体型系数的参考。同时根据风偏调查结果,大部分的跳线风偏事故发生于山地丘陵地区,山地风场会对线路风荷载[12-13]和风偏产生更不利的影响,尤其是风的爬坡效应[14-15]会产生向上的作用力而抵消了一部分跳线的自重,使得跳线风偏更厉害。查阅文献可知,几乎没有针对硬跳线阻力系数和升力系数的规定或研究,更没有考虑其在风攻角情况下的气动力参数及山地风场的影响。
鉴于以上背景,本文通过测力风洞试验获得鼠笼式和铝管式硬跳线在不同风攻角、风速下的阻力系数和升力系数,分析各类硬跳线气动力系数随风攻角的变化特征和屏蔽效应,给出了不同风攻角下各类硬跳线阻力系数和升力系数的建议值,同时提出了考虑山地风场影响的硬跳线体系风偏计算方法,分析水平风加速效应和风攻角对硬跳线风偏的影响,相关研究成果可为输电行业的风荷载和风偏计算提供参考。
1 硬跳线的风洞试验概况
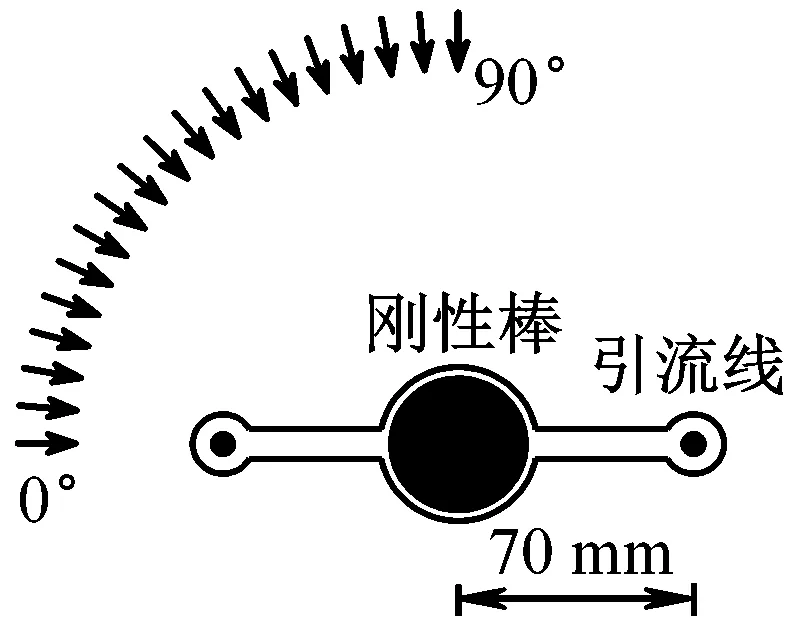
鼠笼式硬跳线是将各分裂引流线分散布置在中央刚性棒周围,通过支撑间隔片将引流线固定于中央刚性棒,刚性棒两端通过软导线与铁塔两侧的耐张线夹相连接,鼠笼式硬跳线一般分为二分裂、四分裂、六分裂、八分裂。铝管式硬跳线将引流线分成两股穿入两根铝管内部,铝管通过支撑间隔片相互固定,铝管两端通过软导线与铁塔两侧的耐张线夹相连接。典型鼠笼式硬跳线(以八分裂为例)和铝管式硬跳线,如图1所示。图1中还给出了风攻角β的定义,水平方向来流为0°,竖直方向为90°。

(a) 鼠笼式八分裂硬跳线
采用风洞测力方法研究不同风攻角情况下各类硬跳线的气动力系数。制作鼠笼式硬跳线二分裂、四分裂、六分裂、八分裂的模型,模型高度为800 mm,中央刚性棒直径为40 mm,引流线直径为6 mm,支撑间隔片由10 mm厚的ABS板激光切割而成。制作铝管式硬跳线的模型,模型高度为800 mm,铝管直径为37.5 mm,铝管间距为150 mm。测试在部分风攻角下硬跳线的气动力系数,通过对称性可获得所有风攻角下的气动力系数,各类硬跳线的横截面和风攻角如图2所示。
(a) 鼠笼式二分裂(风攻角间隔5°)
风洞试验在浙江大学ZD-1大气边界层风洞中进行,试验段截面为4 m×3 m。将试验平台整体垫高20 cm,使测力模型在风洞中避开壁面黏滞层的影响;在模型顶部放置盖板,用来形成模型试验的二维流场。鼠笼式和铝管式硬跳线的风洞试验情况如图3所示。测力天平采用德国ME-SYSTEM公司生产的高频底座测力天平,其最小档的量程为Fxy=20 N、Fz=40 N、Txyz=4 N·m,测量精度为0.3% F.S.,采样频率为500 Hz,各工况采样时间均为60 s。采用图3的装置进行测试,图中鼠笼式仅给出八分裂,通过变化风向角获得的硬跳线气动力系数等同于不同风攻角下硬跳线的气动力系数。

(a) 鼠笼式八分裂
硬跳线阻力系数CD和升力系数CL计算如下
(1)
(2)
式中:FD、FL分别为硬跳线整体所受的阻力和升力平均值;ρ为空气密度,ρ=1.205 kg/m3;v为来流的平均风速;A为硬跳线模型主管和所有辅管的挡风面积总和。以铝管式硬跳线为例,FD、FL方向定义如图4所示。

图4 阻力和升力方向定义
2 硬跳线的气动力系数和干扰效应
2.1 鼠笼式硬跳线的气动力系数
试验获得不同风速下鼠笼式二分裂、四分裂、六分裂、八分裂硬跳线的阻力系数随风攻角的变化,如图5所示。由图5可知:① 随着风速的增大,各分裂数目鼠笼式硬跳线的阻力系数逐渐减小;② 根据对称性可知,在全风攻角范围内,鼠笼式二分裂硬跳线的阻力系数CD关于0°~90°风攻角对称,四分裂硬跳线的阻力系数关于0°~45°风攻角对称,六分裂硬跳线的阻力系数关于0°~30°风攻角对称,八分裂硬跳线的阻力系数关于0°~22.5°风攻角对称;③ 在干扰效应显著的风攻角,四种分裂数目鼠笼式硬跳线的阻力系数均达到最低值。

(a) 鼠笼式二分裂
试验获得不同风速下鼠笼式硬跳线的升力系数随风攻角的变化,如图6所示。由图6可知:① 各分裂鼠笼式硬跳线的升力系数的大小随风攻角的不同产生显著变化;② 升力系数的绝对值随风速的增大呈增加趋势,但高风速下的升力系数几乎一致;③ 由于屏蔽效应的存在,各分裂数目鼠笼式硬跳线的升力系数存在最值,鼠笼式二分裂在5°风攻角下存在约0.75的升力系数,四分裂在35°、40°、55°和60°风攻角下存在约0.35的升力系数,六分裂在10°、55°和60°风攻角下存在约0.25的升力系数,八分裂在18°、27°、63°和72°风攻角下存在约0.2的升力系数;④ 随着分裂数目的增加,升力系数绝对值的最大值逐渐降低,说明多分裂使气流干扰效应加剧。

(a) 鼠笼式二分裂
2.2 鼠笼式硬跳线的干扰效应
各分裂硬跳线的阻力系数和升力系数在不同风攻角下有显著不同,说明在某些风攻角产生了明显的遮挡效应[16]。各分裂情况下硬跳线产生屏蔽效应最大的风攻角,如图7所示。由图7可知:① 二分裂硬跳线在风攻角0°附近时,2、3号杆件分别进入1、2号杆件的尾流区,整体阻力系数逐渐减小,0°时屏蔽效应最大,25 m/s来流时整体阻力系数减少了53.4%;② 四分裂硬跳线在风攻角为45°时,2、3号杆件分别进入1、2号杆件的尾流区,整体阻力系数减少了27.4%;③ 六分裂硬跳线在风攻角为0°和60°时,下风向杆件分别进入上风向杆件的尾流区,整体阻力系数减小了25.1%;④ 八分裂硬跳线在风攻角为22.5°和67.5°时,整体阻力系数减小了16.7%。

(a) 鼠笼式二分裂
2.3 铝管式硬跳线的气动力系数
通过试验获得不同风速下铝管式硬跳线的阻力系数和升力系数,如图8所示。由图8可知:① 随着风速的增大,铝管式硬跳线的阻力系数逐渐减小,高风速下减小效果趋于平缓;② 0°风攻角时屏蔽效应最大,25 m/s来流时阻力系数最大减少57.4%,在0°~25°风攻角范围时,下风向杆件一直处于上风向杆件的尾流区,随着风攻角的增大屏蔽效应逐渐减弱;③ 升力系数的绝对值随风速的增加而增大,增大效果在高风速趋于平缓;④ 15°风攻角时,升力系数最大值可达0.31。

(a) 阻力系数CD
3 风攻角下硬跳线气动力系数建议值
考虑实际的来流风速,以最大试验风速25 m/s的测试结果作为硬跳线气动力系数的建议值。各风攻角各类硬跳线阻力系数和升力系数的建议值,如图9所示。由图9可知:① 各类硬跳线的阻力系数和升力系数随着风攻角的变化均呈现明显的对称性,其中鼠笼式二分裂、四分裂、六分裂、八分裂和铝管式硬跳线分别关于90°、45°、30°和90°、22.5°和67.5°、90°风攻角对称;② 各风攻角作用下各硬跳线的气动力系数可按图9取值;③ 各类硬跳线整体阻力系数最大值可取1.17;④ 各类硬跳线在特定风攻角下均存在较大数值的升力系数,鼠笼式分裂数越小时其最大升力系数越大。

(a) 阻力系数CD
4 山地风场下硬跳线的风偏计算
4.1 山地风场参数
针对某余弦形三维山体进行风洞试验,模型缩尺比为1∶1 000,模型山体底部直径为0.7 m,高度为0.1 m,在模拟A类地貌风场的风洞中进行测速试验,风洞试验情况及测点布置如图10所示。风洞中梯度风高度的试验风速为10.20 m/s,换算成A类地貌60 m高度处风速为8.41 m/s。测试获得离山体表面60 m高度处水平风和竖向风的平均风速如表1所示。表1中P1~P9为迎风面和背风面山坡沿水平坐标均匀布置,其中P1、P5和P9分别为迎风面山脚、山顶和背风面山脚。根据水平风和竖向风,计算获得合速度vc和风攻角α,可以发现:① 山顶位置存在显著的风加速效应,在山顶(P5)和靠近山顶区域(P4、P6)存在显著的水平风加速效应;② 迎风面山坡(如P3)上存在着显著的竖向风,风攻角较大,为典型的“爬坡效应”。查询图9,获得不同风攻角下硬跳线的阻力系数和升力系数,该系数将用于下面的风偏计算。

图10 模型山体和测点位置

表1 实物60 m高度的风速
4.2 硬跳线体系的有限元模型
某硬跳线体系的尺寸如图11(a)所示。硬跳线长度为8 m,左侧引流线为13.348 m,弧垂为2.717 m,右侧引流线为9.668 m,弧垂为1.713 m。导线型号为JL/LB20A-630/45,截面面积为338.99 mm2,单位质量为1 085.5 kg/km,弹性模量为69 000 N/mm2,截面为四分裂形式。悬挂间隔棒的型号为FXBW4-500/100 TX2,串长为5.75 m,串重为107.2 kg。硬跳线为鼠笼式四分裂,长度为8 m,总质量为539.6 kg,总受风面积为1.83 m2,另外硬跳线上还有附加重锤400 kg。

(a) 硬跳线体系的尺寸
在ANSYS软件中采用LINK8单元模拟悬垂绝缘子和硬跳线,采用MASS21单元模拟重锤,采用只承受拉力的LINK10单元模拟引流线,建模时将四分裂的引流线合并为一根,每侧引流线划分为50个单元,有限元模型如图11(b)所示。
4.3 考虑攻角情况的硬跳线体系风偏计算
计算硬跳线体系分布处于图10中迎风面的P1~P9位置,硬跳线处于正迎风位置。A类地貌下10 m高度的设计风速为41 m/s,硬跳线体系平均高度为60 m,该高度的设计风速为50.83 m/s,计算中将表1的风速按比例放大。在风攻角αi情况下,硬跳线的阻力FD和升力FL计算公式为

(3)
(4)
式中:ρ为空气密度;Ai为杆件的挡风面积。
换算为水平向和竖直向的风荷载Fx和Fz分别为
Fx=FDcosαi+FLsinαi
(5)
Fz=FDsinαi+FLcosαi
(6)
计算中对于输电线和悬挑耐张串的阻力系数分别取1.1和1.0。
计算获得硬跳线体系的风荷载,施加于有限元模型中进行风致响应计算,获得硬跳线中点的风偏响应,风偏角β的计算公式为
β=arctan[Dx/(Dg-Dz)]
(7)
式中:Dx为风荷载作用下的水平位移;Dz为风荷载作用下的竖直向位移;Dg为硬跳线与悬挂点的竖直距离。
硬跳线中点的风偏响应结果如表2所示。表2中还给出了硬跳线体系处于地面60 m相同高度时的风偏响应,由表2可知:① 相较地面来流,山地风和风攻角对硬跳线的风偏响应和风偏角产生较大的影响;② 山前迎风坡(P1~P3)为风速的减速区,因此其风偏小于平地情况;③ 风加速效应显著的山顶和山顶附近区域(P4~P6),硬跳线水平竖直位移及风偏角显著增大,在山顶位置达到最大;④ 在背风面的较高处(P6、P7),即使存在负攻角,由于水平风的加速效应,风偏响应也比地面情况显著;⑤ 背风面接近山脚处(P8、P9),风攻角较大,但由于平均风速较小,故风偏响应非常小。

表2 硬跳线中点的风偏响应
5 结 论
本文研究各类硬跳线在不同风攻角、风速下的气动力系数和风偏响应。主要结论有:
(1) 各类硬跳线的阻力系数随风速的增加而减小;而升力系数随风速的增加呈增大趋势,但高风速下的升力系数几乎不变;鼠笼式二分裂、四分裂、六分裂、八分裂和铝管式硬跳线的气动力系数分别关于90°、45°、30°、22.5°和90°风攻角对称。
(2) 杆件之间存在着显著的屏蔽效应,导致在屏蔽效应最显著风攻角下硬跳线的阻力系数存在最小值,鼠笼式二分裂、四分裂、六分裂、八分裂和铝管式硬跳线的最大屏蔽效应风攻角为0°、45°、0°和60°、22.5°和67.5°、0°,25 m/s来流风速下阻力系数比最大值情况分别减少了53.4%、27.4%、25.1%、16.7%和57.4%。
(3) 各类硬跳线均存在一定的升力系数,如鼠笼式二分裂在25 m/s来流风速、5°风攻角时达到0.746,鼠笼式四分裂在25 m/s来流风速、35°风攻角时达到0.380。
(4) 各类硬跳线的气动力系数随风攻角的变化显著,各风攻角下的阻力系数和升力系数建议值见图9,其中阻力系数的保守值可取1.17。
(5) 提出了考虑山地风场影响的硬跳线体系风偏计算方法,山地风和风攻角对硬跳线的风偏响应和风偏角有较大的影响,水平风加速效应显著的山顶附近区域位置,硬跳线的风偏位移和风偏角显著增大,在山顶位置达到最大值。

