统计能量分析方法及应用综述

林天然， 李 震

(青岛理工大学 结构声与机械故障诊断实验室,青岛 266520)

统计能量分析(statistical energy analysis, SEA)是一种用以预测复杂耦合系统中各子系统间高频能量流的常用计算方法。由于复杂耦合结构各子系统在中高频段的模态比较密集，且相邻模态的固有频率间隔通常小于其对应模态的半功率频带，因而在高频响应分析中很难完全分离相邻模态的模态响应，从而无法准确确定各子系统单一模态间的能量传递。同时常用数值分析方法如有限元法(finite element analysis, FEA)和边界元法(boundary element analysis, BEA)由于在高频分析时需要使用大量单元以保证最低计算精度且结果往往存在很大不确定性，因而其在高频响应预测方面具有很大局限性。而SEA由于能够在子系统具体声振特性未知条件下通过统计方法快速估算复杂耦合系统各子系统间平均高频声振能量传递，早在19世纪六七十年代就被成功用于航天器发射阶段产生的高频振动预测并取得良好效果[1]。其后SEA得到越来越多科研工作者的重视并被逐渐推广应用到各种复杂工程结构如船舶舱室声压和噪声传递路径分析[2]；火车高频声振特性分析[3]；隧道内噪声及隧道口向外辐射噪声分析及隧道声学设计[4]等高频声振能量预测中。

SEA方法最早始于1962年Lyon等提出的双线性耦合振子功率流计算方法并在其基础上发展而来。通过计算两个受随机激励且相互独立振子间的功率流，得到了守恒系统耦合结构间的功率流正比于两个子系统的平均模态能量之差，且总是从具有高模态能量的子系统流向低模态子系统的重要结论。此外，Lyon等还推导得到单模态和多模态子系统的相互作用公式，强调了SEA的三个基本参数：模态密度、阻尼和耦合损耗因子对系统响应估算的重要性，为SEA的后续发展奠定了理论基础。几乎在同一时期，Smith[5]在另一论文中也归纳总结出类似于Lyon等提出的SEA方法，并且分析了大型结构共振模态在声源激励下的响应以及由此产生的声辐射，同时建立了模态辐射阻抗与传递函数间的互易关系。随后Lyon在前期基础上进一步把SEA的应用从双振子系统拓展到多振子系统，并分析了振动能量在板-梁-板结构中的传递情况[6]。1966年Lyon[7]提出了一种简单结构模型输入功率和振动响应的计算方法并指出这种方法的本质是在统计意义上将振动能量平均化。1971年Szechenyi[8]利用统计方法估算了直管的模态密度和辐射效率，并讨论了模态在无量纲波数空间中的分布情况。1975年Lyon[9]在其发表的SEA经典专著：《Statistical energy analysis of dynamical systems：theory and applications》里较为完整地归纳总结了自1962年以来SEA理论的发展与应用现状，讨论了SEA在当时工业应用中的可行性与不足之处以及未来的发展方向。1987年孙进才等[10]以及Fahy等[11]几乎在同一时期各自把统计能量分析方法应用于非守恒耦合振子功率流预测并得出以下结论：在白噪声激励下两个振子间的平均功率流不仅与两个子系统的平均模态能量之差成正比，且与各振子的平均能量成正比。Fahy的这一重要结论拓展完善了之前Lyon基于守恒耦合系统提出的SEA基本理论，并成为经典统计能量法(CSEA)演化为一般统计能量法(SEA)的重要分水岭。

SEA根据模态近似原则将一个复杂系统划分为多个相互耦合的子系统并从概率意义上给出各子系统参数[12]。SEA主要参数如模态密度、内损耗因子和耦合损耗因子等可以通过实验方法获取或者采用经验公式估算。同时通过构建各子系统间能量流平衡方程组求得各子系统的平均动态响应及声振能量。相比于其它常用数值计算方法如有限元或边界元法，SEA是一种从统计能量角度分析处理复杂系统高频动力学问题的有效工具[13-15]。

为了便于初学者/研究人员更好地了解统计能量分析方法及其应用以吸引更多科研/工程人员投身于SEA的研究与应用，Fahy于1994年发表了一篇SEA综述论文并系统地总结了SEA的发展状况及优缺点，通过对确定性模型及分析的局限性讨论，详细介绍了SEA频段内平均估算特点以及在分析高频模态重叠问题上的优势，指出了SEA相比于其它数值分析方法的优点以及存在的不足之处，重点讨论了SEA的未来研究方向和工业工程应用前景。孙进才等在1998年又对SEA方法的新进展、新应用进行了一次全面系统的总结，从非守恒耦合系统、守恒强耦合系统和一般耦合系统三个方面详细介绍了物理模型建立和SEA机理的推导过程，同时指出了尚存一些影响SEA拓广应用急需解决的重要问题。二十年稍纵即逝，随着计算机技术的快速发展及应用的拓展，SEA的很多应用及技术条件已发生巨大改变，有鉴于此，本文力图在前人基础上，结合近年来SEA理论及应用的最新发展作进一步的系统阐述和概括。本综述将从SEA发展历程、理论演变、主要系统参数估算方法及应用等方面进行详细地归类总结，为SEA的应用及未来研究方向提供一个尽可能全面的文献参考。

1 统计能量分析方法的理论演变

统计能量分析的理论发展经历了从经典统计能量分析(classical statistical energy analysis, CSEA)到统计能量分析(statistical energy analysis, SEA)的演变过程。经典统计能量分析方法(CSEA)的鼎盛时期通常是指从1962年Lyon等提出的双线性守恒耦合振子功率流理论到1987年孙进才等提出的非守恒耦合系统能量流分析这个阶段，其成功应用案例主要有以卫星运载火箭振动响应为代表的航空航天高频声振预测。但CSEA由于需要满足系统能量守恒以及子系统弱耦合等条件，其在工程应用上存在较大局限性。直到孙进才及Fahy等把统计能量分析方法应用到非守恒耦合振子功率流预测后，并经众多科研人员的不懈努力，CSEA逐渐才被拓展成为一种可适用于一般耦合系统的SEA方法。

1.1 守恒耦合系统

根据Lyon等提出的双线性守恒弱耦合振子功率流理论，可获得在随机外力激励下两个耦合振子功率流的表达式[16]

(1)

(2)

式(1)、(2)直观地表述了两个弱耦合振子间的平均功率流与振子储存能量之差成正比，且能量从高能量振子传递到低能量振子。对于线性守恒弱耦合系统，式(1)、(2)可用下列矩阵表达式表述

[P]T=ω[η][E]T

(3)

式中：[P]T代表各子系统的平均输入功率向量；[E]T表示子系统的能量值向量；ω表示平均带宽中心频率；[η]表示由耦合损耗因子ηij和内损耗因子ηi组成的矩阵。该矩阵方程具有计算简便、适用频带宽的优点[17]。

在实际工程环境弱耦合假设难以成立的前提下，Norton等[18]指出基于弱耦合条件得到的双耦合振子功率流表达式不能任意拓展到多耦合振子组。为了将统计能量分析方法推广应用到更普遍存在的强耦合系统，有学者希望通过修改两个直接强耦合子系统间的耦合损耗因子以提高统计能量分析的预测精度[19-21]，但这方面的尝试由于忽略了不相邻子系统间功率流传递而产生较大预测误差。1995年Finnveden[22]指出无论是直接连接还是间接连接子系统间都存在功率流，忽略间接连接振子间的功率流会严重影响直接连接振子间功率流的预测精度[23]，该结论很快在Cuschieri发表的实验结果中得到验证[24]，并在随后发表的一些研究结果中得到进一步验证[25-26]。

式(4)以三串联耦合振子功率流为基础给出守恒强耦合系统间功率流表达式

(4)

1.2 非守恒耦合系统

由于实际工程系统中能满足守恒弱耦合条件的应用实例并不多[27-30]，故如何把CSEA方法推广应用到非守恒弱耦合系统成为统计能量法在实际工程应用中急需解决的问题[31]。非守恒弱耦合系统必须考虑如何在耦合处存在损耗情况下建立系统能量平衡方程，目前主要使用以下三种方法。

第一种方法是当结构耦合处阻尼较小时，在CSEA能量平衡方程中增添因耦合阻尼产生的损耗项[32-34],此时平衡方程能量传递规律不变,且与CSEA平衡方程形式相仿

(5)

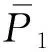
第二种方法是通过引入“消耗耦合损耗因子”用以表示非守恒弱耦合元件的损耗特性，从而避免由于忽略耦合元件能量损耗带来的影响，进而从根本上修正CSEA的能量平衡方程，修正后的能量平衡方程为[36]

(6)

式中，ξ12振子1到振子2间的“消耗耦合损耗因子”，该因子为一表示非守恒弱耦合元件损耗影响的正量，因而与第一种方法中Δη1的作用异曲同工。

第三种方法不仅仅是在能量平衡方程中简单地添加一个正增量项，而是通过引进等效内损耗因子用以修正守恒耦合损耗因子为非守恒耦合因子，此时稳态能量平衡方程依然适用

(7)

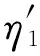
相比于以守恒弱耦合系统所代表的CSEA，以非守恒(一般)耦合系统为代表的近代SEA方法在实际工程应用中更具普遍性与实际应用价值[37-39]。

1.3 瞬态激励耦合系统

CSEA不能得到广泛实际工程应用的另一原因是其仅适用于稳态激励下的耦合系统，为把CSEA理论中的稳态激励假设拓展到瞬态激励，1990年Lai等[40]提出瞬态统计能量分析(transient statistical energy analysis, TSEA)的概念，随后诸多学者发现耦合系统在瞬态激励下的动力学特性可通过一组能量平衡方程描述[41-42]。1998年唐宵东[43]通过比较TSEA与CSEA的异同，将TSEA应用于分析梁-板耦合系统冲击响应谱并较好的验证TSEA的可行性。2019年Langley等[44]用一种类比于普里斯特利(Priestley)对非静态随机过程的描述，推导得到可用于瞬态及冲击激励响应预测的TSEA方程，并以耦合板响应为例，通过比较TSEA预测结果、有限元计算结果及实验结果验证TSEA方法的有效性。

对于包含n个子系统的复杂耦合系统在瞬态激励条件下的动力学响应可通过一组能量平衡方程描述

(8)

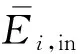
2 统计能量分析主要参数的获取

SEA方法最关键核心的一步是如何将一个复杂系统合理划分成若干相对独立的耦合子系统，然后通过子系统间的平均能量分布描述各子系统的声振特性。其中子系统能量通过该子系统的弹性元和惯性元储存;通过阻尼元损耗；子系统间能量传递通过耦合元实现。基于各子系统间能量流互动关系，通过能量守恒定律可依次建立各子系统的能量平衡方程，从而得到用以描述整个系统能量平衡状态的线性方程组，进而获得各子系统能量及声振响应特性。

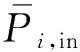
(9)

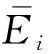
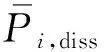
(10)

则该耦合系统的能量平衡方程组可进一步通过下式表示

(11)

式中：Πi,in表示作用于子系统i的激励源对子系统i的平均输入功率；Πi,diss表示子系统i的内阻尼平均损耗功率；Πij表示从子系统i传递到子系统j的平均功率流。

由于子系统间的平均功率流正比于两个子系统的平均模态能量之差，且总是从具有高平均模态能量的子系统流向低平均模态能量的子系统，因而子系统间的平均功率流可通过下式表示

(12)

式中，ni为子系统i的模态密度。

由于耦合子系统间功率流满足互易原理，因而有

Πij=-Πji

(13)

即niηij=njηji，将式(9)、式(12)和式(13)代入式(11)可得到以下矩阵表达式

(14)

式中，ηmm代表子系统m的总损耗系数。由式(14)可以看出准确获得主要参数如模态密度、内损耗因子和耦合损耗因子是成功应用统计能量分析方法预测系统高频动力学响应的关键。2016年Antonio等[45]指出子系统能量与内损耗因子和耦合损耗因子紧密相关，并给出输入功率、耦合损耗因子以及结构物理参数间的近似关系。但由于复杂耦合系统的主要参数一般难以准确获取，许多科研工作者就如何精确快速估算SEA的各种系统参数展开了大量研究[46-49]，并提出了一系列参数估算方法，本节将对现有SEA各个主要参数的估算方法进行一个全面的归纳总结。

2.1 模态密度

模态密度是指一个系统在某一频段内单位频率的模态数，是一个代表系统在外力激励下产生共振响应能力的重要指标[50]。一般来说，模态密度越大，结构从宽频激励中吸取能量的能力越强[51]。目前通常采用的模态密度估算法主要有解析法和实验法。Lyon和姚德源通过解析法计算了简单典型结构如梁、板和壳的模态密度，并给出较为准确的理论公式[52-53]。但由于实际工程应用中更多的是复杂不规则结构，其模态密度很难通过解析方法准确估算，因此通过实验测试方法获得子系统模态密度显得尤为重要[54-57]。Clarkson[58]在1981年提出一种基于结构激励点导纳获取模态密度的方法，并通过实验加以验证[59]。目前基于结构激励点导纳实部平均值计算模态密度(即点导纳法)成为主要实验方法[60]，例如点导纳法被用于测量铝蜂窝夹层结构的模态密度[61-62],薄铝板的模态密度[63]等。

通过点导纳法估算模态密度n(ω)的表达式为

(15)

式中：M表示结构质量；ω2、ω1分别是带宽为Δω的频率上下限;Y(ω)为结构输入点导纳。其表达式为

(16)

其中A(ω)和F(ω)分别表示系统在外力激励下的加速度响应和激励力的傅里叶变换。

近年来越来越多的学者尝试结合有限元方法对不同耦合系统进行模态密度的估算。Yan等[64]于2002年提出一种通过有限元方法估算中低频区双、三耦合子系统的模态密度，并通过实验验证数值解的准确性。2010年孔宪仁等[65]基于特征系统算法提出了一种估算模态密度的方法，并对铝蜂窝夹层结构的小卫星模型进行数值仿真，进一步验证该算法的可行性。2019年Chen等[66]提出一种采用有限元法建立热环境下能量流模型并估算受雨流载荷的简支L型折板模态密度的算法，并指出仅受温度影响时板的模态密度与耦合损耗因子的变化趋势相反。

2.2 内损耗因子

内损耗因子是指一个系统在某一频段单位频率、单位时间内损耗能量与平均储存能量之比[67]，能够代表由系统阻尼特性决定的能量损耗能力，因此内损耗因子的研究对结构动力学响应和声传递特性具有重要意义。结构子系统的内损耗因子可以表示为[68]

η=ηs+ηr+ηb

(17)

式中，ηs、ηr和ηb分别表示结构损耗因子、声辐射损耗因子和边界损耗因子。测量频带内平均内损耗因子通常使用实验测试方法，其中功率输入法和脉冲响应衰减法是两种比较常用的实验测试方法[69]。

功率输入法的基本思路是通过给子系统提供一个稳定的输入功率并测量系统在稳态下的平均响应能量来确定频带内平均内损耗因子。2007年Liu等[70]基于有限元模型，通过计算三合板的输入点导纳和传递导纳估算其内损耗因子。

子系统频带内平均内损耗因子表达式为

(18)

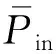
(19)

(20)

式中：N为测点的数目；Mi表示第i个测点的有效质量；Yif(ω)表示激振点到测点i的频率响应函数。

系统在受到稳态激励时，由于试件和激振器的连接导致接触阻尼的增大从而影响到内损耗因子的测量精度[71]。2009年Martarelli等[72]使用激光扫描多普勒振动仪进行蜂窝板表面速度响应测量，该测量方法极大地提高蜂窝板内损耗因子的测量精度。

使用脉冲响应衰减法对系统频带内平均内损耗因子进行测试可以有效规避因测试系统与测试对象连接带来的内损耗因子测量误差。脉冲响应衰减法的基本思路是借助结构中振动能量的衰减率来估算频带内平均内损耗因子，通过对结构进行脉冲或随机激励，测量激励后结构响应的衰减信号进而估算内损耗因子。衰减率的获取方法主要包括基于Hilbert变换的信号幅值包络法和Schroeder积分法[73-75]，其中单次测量的Schroeder衰减曲线与多次测量的信号总体平均衰减率结果相仿，而Hilbert变换包络线则更为平滑[76-77]。

采用脉冲响应衰减法测试频带内平均内损耗因子的表达式为

(21)

式中，RD表示系统响应曲线的衰减率(decay rate,DR)，可通过计算衰减曲线幅值对数值的斜率求得

(22)

式中,v1、v2表示t1、t2时刻系统的速度或加速度响应包络线幅值。在实际测量中RD的值会随时间改变，故在获得数据过程中往往会因为带有主观性而导致测量误差[78]。

2.3 耦合损耗因子

耦合损耗因子是一个体现SEA子系统间能量传递效率的重要参数，即子系统间耦合作用大小的度量。目前获取耦合损耗因子常用的方法包括试验方法、波方法(wave method)、功率输入法(power injection method，PIM)、有限元法(finite element analysis，FEA)、有限元-功率输入法(finite element analysis-power injection method，FEA-PIM)和双模态方程法(dual modal formulation，DMF)等。

由于试验方法对工作环境要求较高、资源耗费大，因此除了用于科学研究外，鲜有实际工程应用案例[79]。1994年Cacciolati等[80-81]对三点耦合平板进行试验测量，推导出简单耦合结构耦合损耗因子的估算方法。2013年Pankaj等[82]利用波方法获取简单耦合结构如耦合梁、耦合板的耦合损耗因子方法，令人遗憾的是其未能将该方法进一步拓展应用到复杂结构的耦合损耗因子估算。针对建筑相邻房间隔声性能的研究，2016年Dijckmans[83]基于Pankaj的研究方法指出半无限板在扩散声场假设下可通过波方法估算其耦合损耗因子，进而确定两墙板连接处的能量传递情况。目前功率输入法是一种获取耦合损耗因子应用最为广泛的方法，1980年Bies等[84]通过建立两个耦合板模型的线性功率平衡方程估算其耦合损耗因子，并基于功率输入法对耦合板进行损耗因子矩阵预测。Lalor[85]在1989年对功率输入法进行了优化，尝试将损耗因子矩阵分开求解从而提高结果的精确度并大大降低计算量。2013年Secgin[86]基于功率输入法对复合材料耦合板的耦合损耗因子进行计算，同时验证在中频段采用功率输入法的精确性。2015年Putra等[87]将基于功率输入法估算所得的汽车内部SEA模型耦合损耗因子用于估算汽车内部声压级，发现其与实验测量结果吻合良好。2016年Mandale等[88]针对不同连接方式的矩形耦合板连接处进行了耦合损耗因子计算，将实验结果与结合能级差分法估算的理论值进行对比，在验证方法可行性的同时进一步发现通过螺栓连接的耦合板连接处的耦合损耗因子要高于螺纹连接方式。2002年Yan等指出有限元法也能够精确获得中低频段结构的统计能量分析参数，但在高频区由于需要非常精细的网格划分，限制了有限元法在高频参数估算的应用。鉴于有限元法在中高频预测的局限性，许多科研工作者采用结合有限元和功率输入法的方法用于获取耦合损耗因子[89-91]。Mace等[92]以三耦合板系统为例，利用有限元法估算子系统的输入功率和能量并利用功率输入法估算系数矩阵的系数，得出子系统应力分布、质量分布和刚度分布矩阵分别受到激励分布特性、系统质量和刚度特性影响的重要结论。2017年陈强等[93]基于有限元-功率输入法提出一种适用于热环境中的SEA方法，并分析了热效应对复杂结构SEA参数的影响。虽然许多研究结果证实了有限元-功率输入法在计算耦合损耗因子的有效性，但同时也存在稳定性较差的问题。双模态方程法是一种基于子系统在耦合边界的模态参数直接估算耦合损耗因子的方法，具有计算效率高、计算耗时短的优点。2001年Maxit等[94]通过对简单耦合结构的子系统进行解耦分析，进而利用双模态方程法估算梁、板结构子系统间的耦合损耗因子，指出双模态方程法更适用于工业中大型复杂系统。2016年孔宪仁等[95]采用有限元-双模态方程法对典型L型耦合加筋板进行耦合损耗因子预测精度研究，结果显示其计算效率比有限元-功率输入法提高了近一倍，也证明双模态方程法可以高效精确估算复杂结构的耦合损耗因子。

3 不同工况下统计能量分析研究

3.1 不同激励条件下的SEA研究

开展统计能量方法声振分析时一般假定外部激励为随机激励。1964年Lyon等[96]首次将SEA方法用于随机激励条件下简单结构的耦合问题研究，通过对单振子与板的连接系统模型及两个板的连接系统模型分析，指出SEA可以用于估算在结构连接处因随机振动产生的能量。基于Lyon双振子耦合模型的成功案例， Newland[97]在1966年将SEA拓展应用到三振子耦合结构中，并对随机激励下系统的耦合损耗因子给出定义。近年Lin等[98]通过理论计算讨论了在确定力或确定力矩激励条件下耦合板间的能量流关系，并发现当激励源跟耦合板边界的距离超过1/4板挠曲振动波长时，SEA方法可用于预测确定激励源条件下耦合板间的平均能量流。

针对激励形式的差异，输入功率的估算方法也需随之调整。1990年Norton等[99]在对输入功率计算的研究中提出：在受到连续、宽频随机激励时建议采用互谱方法估算输入功率；在激励为确定性瞬态时采用阻抗方法估算输入功率。2002年Renji等[100]在Norton的理论基础上基于蜂窝板模态密度公式和激励力对复合材料蜂窝夹层板结构进行输入功率计算，并对其内损耗因子进行估算。

与此同时，关于SEA输入相关性的研究也有了长足进展。针对系统分别受单点激励和双点激励的不同情况，1994年刘明治等[101-102]采用等效输入功率列阵方式得到受相关激励下功率流是由比例功率流和相关功率流组成的结论。同一时期张建等[103-104]也进行了一系列关于SEA相关激励的研究，张建分析讨论了在任意输入条件下耦合振子的能量分布，并推导出功率平衡方程及有关功率项的计算公式。2002年张建[105]基于相关或互不相关激励条件下非守恒耦合系统的SEA机理，提出两个相似SEA系统间的能量关系可通过利用已知系统预测未知相似系统方法得到，并通过理论及实验验证该方法的合理性。

3.2 中低频频段内的SEA研究

SEA方法主要用于预测高频频段复杂耦合结构子系统间的能量流，但许多科研工作者也不断探索将SEA方法推广应用到中低频段动力学分析的可能性。1997年Chol等[106]提出在考虑模态密度与边界条件关系时，在中频段应用SEA方法也可以得到精确结果。2005年王毅刚等[107]通过理论计算和实验测量类似于飞机舱体结构的圆柱壳结构内部声压级，并对简单板壳结构进行数值仿真与实验验证，结果证明该研究对SEA方法适用频率下限的界定具有重要指导意义，同时指出储存能量较多的子系统对复杂系统的低频SEA分析影响较大。2008年王毅刚等[108]通过对不同SEA模型进一步深入研究，分析讨论了复杂耦合结构中SEA子系统模态数与下限分析频率之间的关系。王毅刚发现当子系统具有足够多的模态时，储存能量较少的子系统对复杂系统的低频SEA分析影响较小。Lin等于2011年发表的一篇理论分析文章里提出当外力激励与板耦合边界的距离超过1/4板挠曲波长时，SEA方法可用于预测确定激励源条件下耦合板间的平均能量流。同年李冰等[109]开展了四种不同激励条件下飞机舱内噪声中频噪声预测研究，通过对比仿真和实验结果验证混合FEA-SEA比SEA能更好的预测舱内中频段噪声。2014年秦朝红等[110]采用FEA-SEA法对飞行器典型结构件开展了中频力学环境预示参数识别及建模技术研究，其结果与混响室噪声实验数据对比吻合良好。2015年毛杰等[111]提出多物理场耦合激励下的高速列车车内结构中频噪声辐射计算方案，分别采用快速多极边界元、刚性多体动力学和大涡模拟结合Ffowcs Williams-Hawkings(FW-H)声类比法提取轮轨噪声，同时对二系悬挂力及空气动力噪声进行仿真，结果与实验声压级对比误差符合工程要求。2016年张永杰等[112]基于H-混合模型法，针对梁板组合结构的中频振动问题建立了FEA-SEA模型，并通过模态试验对模型进行了验证。同年Yan等[113]基于FEA-SEA法和Monte Carlo法对振动声耦合作用下的飞机模型的结构振动和座舱声场响应进行了数值分析，通过试验验证该方法的可靠性。2018年Gao等[114]提出一种FEA-SEA法用于分析耦合系统中频声振特性，通过计算声腔各点声压发现该方法不仅具有较小的自由度，同时能自动满足外部无限远声场的Sommerfeld辐射条件。同年Wu等[115]建立了梁板组合结构的ES-FEA-SEA混合模型，将基于边缘的光滑有限元技术应用于梁板组合结构的三维有限元模型中, 通过对比ES-FEA-SEA法和FEA-SEA法的结果，发现混合ES-FEA-SEA法可用于求解梁板组合结构中频振动问题。Abdullah等[116]在2019年提出一种基于模态阻抗点、线、面连接的复杂耦合系统的SEA方法，通过对某柜体模型进行理论计算以及大量实验验证该方法在复杂系统中频声振特性分析的可行性。同年Hawes等[117]将FEA-SEA法推广应用到冲击和时变载荷作用下的结构中频响应计算，在瞬态条件下研究了子系统产生的混响力与其内部能量之间的扩散场互易关系，通过与梁板耦合结构的FEA模拟结果比较，发现使用该FEA-SEA法可获得较高的计算精度。2020年Gao[118]针对复杂组合系统的中频振动问题提出一种混合FEA-SEA法，为避免过大的计算量引入动力凝聚来降低有限元单元的阶次，从而显著降低了总动力刚度矩阵，并通过算例验证该方法的有效性和收敛性。

4.3 SEA的响应统计估算

由于SEA是一种基于统计意义的声振特性分析方法，其有效性和精确性受到参数估计，子系统划分等多方面因素影响，具有一定的不确定性。因此完整有效的响应统计估算对成功分析SEA数据结果尤为重要[119]。Langley等[120-123]提出作为SEA的后处理模块，响应统计估算应当包括：随机系统在点载荷作用下能量密度的统计、具有随机性质的动态系统响应统计量和SEA响应预测等。1962年Schroeder[124]通过对声容器单点响应分析，得出在足够高的频率下模数平方传递函数是指数分布的结论。1969年Lyon发现该结论仅在较高频率时成立，且模数平方传递函数的标准方差偏大[125]。类似的结论在1978年Waterhouse[126]的研究中也有所提及。但是随着研究的逐步深入，越来越多的科研工作者对Lyon和Waterhouse的结论提出了疑问。1981年Davy[127]指出当应用“最近邻(nearest neighboring)”分布假设时，测量值和理论值的吻合度要比Lyon的结果高，且通过理论计算和大量实验分析进一步指出Lyon和Waterhouse方差估计法的误差[128]。1989年Weaver[129]提出动态系统响应统计估算应满足(Gaussian orthonormal ensemble, GOE)频率空间等频率分布假设，该观点的提出标志着SEA响应统计估算的新发展。随后Weaver通过高斯正交集合频率空间的响应统计估算方法得到的预测值与实验结果基本一致[130-133]。1996年Burkhardt等[134-135]提出了复杂系统模态衰减率期望分布的修正模型并讨论了模态阻尼和模态延迟率对响应统计估算的影响。2005年Manning[136]提出SEA响应统计估算应分“三步走”，分别从输入功率估计、传递函数估计和从能量角度分析声振响应特性三方面对SEA系统进行响应统计估算。2008年Zheng等[137]通过大量实验验证了简单耦合结构振动响应估算方法的稳定性，同时推导出不确定动态结构振动响应的计算表达式并得到实验验证。2011年廖庆斌等[138]在此基础上进一步分析复杂耦合动力学系统的SEA响应统计估算，并讨论系统响应统计估算在各种形式激励条件下产生的偏差以及载荷参数的确定方法。2019年Andrade等[139]通过对一个由平板与封闭声场耦合的结构声学系统的实验测量，验证了统计能量分析模型预测能量均值和方差的有效性。

4 SEA在实际工程中的应用实例

SEA最早被用于航空航天系统的高频声振预测并取得了显著效果[140-143]， 随后被逐渐应用到工程实践中的其它领域，如舰船、汽车、火车、建筑和核反应堆等实际工程问题的声振特性分析。本章节将对SEA在实际工程中的成功应用实例进行概括总结。

4.1 SEA在航天航空中的应用

SEA在航天航空领域如航天飞机、导弹和火箭的高频声振预测方面有许多非常成功的应用案例[144-147]。2002年Bremner等[148]总结了SEA在飞机舱内减振降噪和飞机内部结构声学设计的最新研究进展。2016年赵欣等[149]详尽地介绍了SEA在航天器火工冲击地面试验以及环境预示的应用，并从航天工程急需改善的角度指出未来航天器领域发展应重点探索的研究方向，本节针对航天航空方面几个具体应用方向所发表的文献进行综合介绍。

飞机机舱的噪声预测一直是SEA方法应用的一个热门方向。1968年Jolly等[150]首次尝试使用SEA对随机激励下飞机机舱的声振响应进行分析，通过将机舱结构和舱内声场看作一个耦合的动态系统对舱内声压水平进行估算，但因预测结果缺少实验验证，故不能保证舱内声压水平预测值的可靠性。Hay[151]在此基础上比较了机舱内声压测量值与SEA预测值，但所得结果吻合度较差。1983年Miller等[152]通过SEA方法研究了飞机舱室内部噪声水平，通过对飞机简化模型进行舱内声压测量发现在较高频段SEA预测值与实际测量值有良好的一致性，进而指出SEA方法可用于飞机舱体模型高频声振预测。同年美国宇航局(NASA)研究了飞机航行状况下舱内噪声及减振降噪方法，通过分组形式对S-76直升机的模态响应进行分析[153]，并在模拟飞行条件下对实际模型进行大量实验验证，发现机舱噪声及振动响应的测量值与SEA预测值高度吻合。20世纪90年代波音公司对波音727飞机进行地面声振实验，通过建立螺旋桨相关装置的SEA和FEA模型预测机舱内部低频噪声并对分析方法进行讨论[154-155]。波音公司的另一组研究人员通过对S-92直升机舱内噪声进行类似实验分析[156]，进一步证明SEA能够广泛应用于各种型号飞机模型舱内噪声预测。2019年Giuseppe等[157]为提高驾驶员与乘客在飞机舱内的舒适性，基于SEA对机身不同位置进行中高频声压级数值计算，进而讨论分析不同机舱结构设计对隔音效果的影响，同时提出一种将黏弹性阻尼层嵌入玻璃窗的隔音方式用以减小因机身表面湍流边界层造成的噪声。

SEA在航天航空领域应用的另一个热门方向是关于各类飞行器声振特性环境试验研究。飞行器在高速飞行过程会受到振动、冲击以及高温高声强环境的影响，其噪声源主要来自三方面：发动机在高速推进过程产生的喷气噪声；燃料燃烧引起飞行器结构内部空腔共振产生的噪声；超高速飞行过程中飞行器表面湍流层所导致的空气动力学噪声[158]。此外飞行器表面由于气动加热产生的高温载荷也会对飞行器本身造成振动损害，并对飞行器硬件结构和有效载荷造成重要影响，严重时可导致器件失效和设备的疲劳破坏[159-160]。为避免上述不良后果，飞行环境下飞行器的适应性验证以及飞行器声振特性试验研究就显得尤为重要[161]。2005年Shorter等[162-163]针对飞行器高温、高声强环境提出了一种基于混合FEA-SEA方法用以解决中频声振问题，Langley指出SEA能够分析系统中参数不确定的子系统，进而预测不确定多模态子系统的振动特性[164-165]。

由于SEA能够较好地预测火箭喷流噪声和空气动力噪声等宽带激励下的动态响应，因而通过SEA对火箭发动机噪声进行数值模拟与声振分析成为近年来的一个新研究热点[166-167]。发动机作为火箭发射的主要动力推动装置在工作过程中会产生高量级声振，其噪声主要来源包括燃烧室不稳定的燃烧和喷流噪声[168-169]。2015年朱莹等[170]应用SEA方法对火箭发动机模型进行全频段声振响应分析，得到喷流噪声声压级与喷流流场湍流动能成正比的结论。相比于动力学预测的其它两种常用方法(相似结构外推法、传统模态法)，SEA由于仅从能量角度估算频率域响应的统计平均值而不用考虑被研究对象的具体细节，已逐渐成为解决火箭、导弹等的宽带高频动力学预测的常用方法。2002年Iadevaia等[171]应用SEA对导弹板状结构进行数值预测和实验测试，验证了SEA可以有效用于瞬态冲击激励下导弹的声振特性预测。

4.2 SEA在车辆中的应用

SEA方法刚出现不久就被成功用于估算车辆振动和内部空间平均噪声值，并逐渐被推广应用到车辆工程的诸多领域[172-174]。1997年Pierre等[175]在复杂车辆结构振动能量传递的研究进展综述中指出，由于复杂车体结构中随机参数的不确定性严重影响其它高频动力学方法的应用，把SEA方法推广应用到车辆工程高频声振预测意义重大。目前SEA主要被用于预测汽车内部声振特性及复杂车体结构间的能量传递路径[176-177]。2010年Chen等[178]基于SEA方法提出一种车辆内部声学材料优化处理办法，通过测量材料的吸声系数和传输损耗，讨论各子系统对车内噪声的能量贡献，进而提出降低汽车内部噪声级的解决方案。2013年焦映厚等[179-180]提出采用加筋或添加阻尼材料的方式可以有效降低车身板件的振动水平。在此基础上贺岩松等[181]于2016年对声学材料进行优化改进并提出一种FEA-SEA混合法用于车身板件减振降噪分析，并讨论汽车驾驶员头部声腔声压级的变化趋势。2019年Lee等[182]利用SEA法对汽车内部声压级进行预测，分析讨论了不同部件的声传递损耗以及对车内声压级水平的贡献。Chen等[183]尝试使用SEA和半无限流体法建立轿车车外噪声预测模型，通过比较实验和预测结果发现SEA方法不仅能简化建模步骤，同时能较准确的预测车外噪声。

SEA方法不仅被用于小型轿车声振响应和传递路径预测，在大型载重类工程车辆中也有许多成功应用案例。1997年Borello[184]利用SEA方法预测大型货车驾驶室的噪声传递路径，并基于外部噪声负载和底盘机械力作用条件下预测驾驶室内的噪声响应。2007年Burkett[185]使用SEA分析卡车驾驶室板件振动响应和内部声压响应，讨论了不确定声源对噪声响应的影响，进而提出一种在驾驶室设计初期控制机载噪声的优化方案。

近年来随着铁路运输的快速发展以及列车速度的不断提高，空气动力学对列车进一步提速的瓶颈制约逐步显现[186-187]。而由于SEA方法能很好地处理高宽频带随机载荷激励下的复杂结构动力学问题，其在高速列车声振特性及提速方面的应用显得意义重大[188-190]。高速列车噪声来源主要有牵引噪声、轮轨噪声和气动噪声，当列车速度超过300 km/h时气动噪声成为主要噪声源[191]。高速列车气动噪声的计算方法主要包括近场流场计算和远场辐射计算[192-195]，2017年刘加利等通过对车体结构子系统湍流边界层输入激励的计算，提出一种结合大涡模拟(large eddy simulation，LES)方法分析高速列车车内中高频气动噪声特性的SEA方法用于计算列车各子系统声腔的气动噪声A计权声压级水平。2018年王毅刚等[196]结合风洞试验、计算流体力学和SEA法研究车外空气脉动及其产生的气动噪声向车内的传播特性，发现车内气动噪声主要来自于车窗、前后风挡;车外脉动压力远大于声场,但声场主导中频偏高频车内噪声,脉动压力在中频偏低频作用明显;风挡向车内的声能传播,主要以车外空气脉动激发的振动传递为主。2020年唐荣江等[197]建立车内噪声分析预测SEA模型，通过测量各个工况下车身的振动激励和声压激励，并将驾驶员头部声腔噪声声压级结果的仿真结果与实验结果对比验证SEA模型预测车内噪声的精确性。同年Liu等[198]使用FEA-SEA法对钢-混凝土组合的铁路桥梁进行结构噪声分析，通过合理简化模型得到桥梁结构噪声级与列车速度的关系，并通过实测进行验证。

4.3 SEA在船舶中的应用

由于船舶舱室噪声主要为中高频噪声，故SEA是分析船舶噪声及噪声传递路径的关键技术手段[199-200]。传统的矢量相干叠加法在分析船舶舱室中高频振动噪声问题会存在较大误差，并且矢量相干叠加法的传递路径分析不适用于SEA，相比之下基于能量叠加原理的非相干叠加法更便于SEA应用[201-202]。1993年Magrans[203]利用幂级数展开法，按路径阶次分析船舶结构间能量传递路径，但由于该方法计算量过高从而限制其在实际工程中的应用。1995年Hynná等[204]提出一种预测大型焊接船舶结构声传播的SEA方法，并对一个具有5 000多个单元，17 000个耦合路径的邮轮模型进行计算，验证了SEA的高效性；同时通过比较扫频船、木制集装箱船和客轮的计算结果和实测结果，验证SEA的准确性。1996年Craik[205]提出一种损耗因子共享法即逐条路径分析法用以确定能量主要传递路径，该方法的提出为后续SEA在船舶噪声预测和能量传递路径分析应用上奠定了基础。但损耗因子共享法在处理大型复杂耦合系统时无法得到所有可能的能量传递路径，因此与SEA高效便捷的统计特性背道相驰。2009年Bot[206]将熵的概念引入SEA，并从热力学角度丰富完善SEA在船舶工程中的应用。2014年高处等[207]在Bot的研究基础上将SEA系统等效为声振熵赋权图，利用删除边算法求得能量传递的主要可能路径, 从而验证声振熵赋权图法预测船舶舱室噪声传递路径的有效性，该研究方法可用于指导大型、超大型游轮的噪声传递与能量分布分析。2017年张文春等[208]提出一种基于SEA赋权图的船舶舱室噪声传递路径分析方法，通过对子系统进行数值模拟预测能量在船舶舱室中的传播机理。张文春等给出的结构间能量传递规律为SEA在船舶行业的声振控制和减振降噪优化设计提供了一个可行方向。2018年Avcu等[209]基于SEA建立振动声学模型中主要能量路径排序的系统方法，根据模拟结果验证路径修改后对船舶结构振动能量水平降低的可靠性，同时指出基于SEA的能量路径排序法可以快速预测复杂船舶结构的声振特性，进而找到每条路径的能量输出并修正存在问题的路径。2019年吴晓佳等[210]基于SEA对邮轮舱室噪声进行预示研究，利用VA One建立邮轮全船的SEA仿真模型，通过模拟各舱室噪声频谱图和总的声压级发现主要噪声来源，进而比较各降噪控制方案得到最优降噪效果。同年王淅铖等[211]指出虽然SEA法处理复杂船舶结构具有其优势性，但是由于过细的建模会导致计算量过大和预测精度低的问题，对此提出一种基于SEA方法的典型船体板架结构简化建模的等效原则，并通过误差分析验证其合理性。

5 结 论

本文从理论及实际应用实例两方面分析总结了SEA从20世纪60年代初提出至今近60年的发展历程。文章从经典统计能量分析(CSEA)方法入手详细介绍了其演变为可应用于大部分工程问题的多子系统耦合、非守恒的现代统计能量分析(SEA)众多科研工作者所做的努力和贡献。文章同时详细介绍了统计能量分析方法各种参数的估算及测量方法以及在航天航空、车辆及船舶工程方面的成功应用实例，为从事SEA方面研究的研究人员提供一份尽可能全面的参考文献，同时为初学者提供一份详尽的入门资料。

经过众多科研工作者的多年努力，统计能量分析法及其工程应用有了长足发展，但尚有一些理论与应用方面的问题值得科研工作者进一步深入探索研究，主要有但不限于以下几方面：

(1) 建立新的理论公式及实验方法用于准确计算或测量复杂耦合系统的耦合损耗因子以提高各子系统间能量流及响应的计算精度，针对常用SEA应用对象如飞机舱室、船舶舱室及相邻舱室传递能量路径等的系统化建模方式和声振特性预测方法；

(2) 有效结合有限元(FEA)及其它分析手段将统计能量分析方法拓展应用到中低频段实现全频域系统动力学响应分析，在保证高频预测精度的同时针对不同模型进行合理简化从而实现高效、精确的中低频分析；

(3) 针对工作工况愈发复杂的现代工业环境，稳态或瞬态确定激励条件下复杂耦合系统振声响应的统计能量分析方法是急需拓展的研究方向。