多跨格构式构架气弹模型设计与风洞试验

李 峰， 邹良浩， 陈 寅， 梁枢果

(1.武汉大学 湖北省城市综合防灾与消防救援工程技术研究中心,武汉 430072；2.中国电力工程顾问集团中南电力设计院有限公司，武汉 430071)

格构式构架是广泛应用于输变电、通讯和广播电视等方面的结构，是一种典型的风敏感结构。根据用途的不同，格构式构架可设计为独立式单塔和复杂多跨度构架。独立式单塔包括输电塔、通讯塔和格构式电视塔等，此类结构高宽比较大，具有典型的高耸结构特性。而复杂多跨度格构式构架广泛应用于变电构架中，其兼具高耸和大跨度结构的特性。

目前，对于独立式单塔风荷载及风致响应的研究较为丰富。主要包括：基于准定常假定的结构顺风向风荷载、风致响应以及气弹效应的研究[1-4]；由高频测力天平(high-frequency force balance, HFFB)风洞试验测结构基底弯矩或扭矩得到线型振型广义荷载谱[5]，并通过振型修正得到更精确的基阶和高阶振型广义荷载谱[6-7]。在得到风荷载模型后，基于结构随机振动理论进行风致响应计算。另一方面，通过现场实测、气弹模型风洞试验直接测得结构风致响应[8-23]。

在复杂多跨度格构式构架方面，对其风荷载与风致响应的研究较少。由于多跨格构式构架具有空间结构的复杂性，其风荷载与风致响应评估较复杂，潘峰等[24]基于多阶模态力法和模态解耦原理，运用有限元软件在时域内计算了某1 000 kV大型变电构架的风致响应。牛华伟等[25]基于HFFB风洞试验，得到了某500 kV全联合变电构架的体型系数，运用有限元软件模拟风荷载时程得到了风振系数。此方法虽然具有较高的经济性，但是由于目前缺少准确的多跨格构式构架的风荷载模型，尤其是忽略了横风向风荷载，可能导致较大的误差。HFFB技术是通过测量结构基底弯矩或扭矩得到线性振型的广义风荷载。对于多跨度的格构式构架，其结构各阶振型频率较接近，振型复杂，很难由结构基底整体弯矩或扭矩得到其各阶振型广义风荷载。准定常假定可以得到结构顺风向风荷载并进行结构顺风向风致响应分析，但是并不能得到结构横风向风荷载。现场实测可测得实际多跨格构式构架的风振响应，直接检验风洞试验和理论计算结果。但该方法周期长，费用高，得到的风荷载信息十分有限。气弹模型模拟了结构的动力特性，并可考虑其气动弹性特性，通过风洞试验测得结构的风致响应，能够较为全面地反映风对结构的作用。因此，在目前条件下，气弹模型风洞试验是研究多跨格构式构架风致响应经济、有效和可靠的方法。

本文以典型1 000 kV两跨变电构架为背景，采用刚性节段加V型弹簧片法设计制作气弹模型，并进行了风洞试验，主要研究了多跨格构式构架在不同风向角下和不同风速下风振响应的变化规律，得到格构式构架风振响应的特性，并采用惯性风荷载方法和阵风荷载因子方法进行了风振系数的计算与分析，得到的结论对于工程设计有一定的参考价值。

1 气弹模型

1.1 气弹模型设计与制作

由于多跨格构式构架一般由多个独立格构式塔架与格构式横梁连接构成，结构振型密集，连接杆件多，阻尼比小，设计制作这类空间结构的气弹模型较为困难。目前，对独立格构式塔架结构气弹模型的设计与制作较多。基本设计方法包括集中刚度法[9-10]、离散刚度法[11-20]与刚性节段加V型弹簧片法[21-23]。其中，集中刚度法是通过变截面的刚芯模拟结构的抗弯刚度，表面加轻质外衣模拟结构外形，多用于外形沿高变化小的独立式结构，如单杆输电塔等。虽然基于该方法制作模型较为简单，但该方法得到的气弹模型振型可能与实际结构相差较大，且轻质外衣的附加刚度会导致气动力传递失真。离散刚度法以完全模拟结构特性为目标，需要对每个杆件的刚度和几何进行模拟。由于材料的限制，在进行模型制作时，采用钢芯模拟结构刚度配合外衣模拟结构的外形。这种模型制作方法能基本模拟各个杆件的刚度，因此能准确模拟结构的频率与振型，可进行结构风致破坏试验。但是如果要设计制作满足刚度相似的完全气弹模型，计算得到的钢芯材料尺寸较小，容易出现刚度损失，并且该方法模型制作复杂，使得结构阻尼比往往偏大。对于单塔这种简单的结构，采用此方法还勉强可以满足阻尼比的要求。但对于复杂多跨度格构式构架，由于受力杆件多，耗能多，可能会出现过大的阻尼比。刚性节段加V型弹簧片法是把结构按几何相似分成若干刚性节段，各段质量分布与原型一致，节段间通过V型弹簧片连接，提供结构的刚度，类似于多质点模型。这种气弹模型制作方法没有严格模拟结构的刚度分布，因此无法进行结构破坏极限风荷载研究。但是该气弹模型杆件连接简单，耗能部位少，只要调节好各个节段处的刚度，就能较好的模拟结构质量、频率、振型和阻尼比，对进行结构风致响应风洞试验研究具有独特的优越性。通过以上比较分析，对于多跨格构式构架结构，由于其结构更为复杂，刚性节段加V型弹簧片法可以解决离散刚度法的材料刚度不足和阻尼比过大的问题，也能很好的反映多跨格构式构架整体响应情况。因此，采用刚性节段加V型弹簧片设计制作多跨格构式构架气弹模型是较为合适的选择。

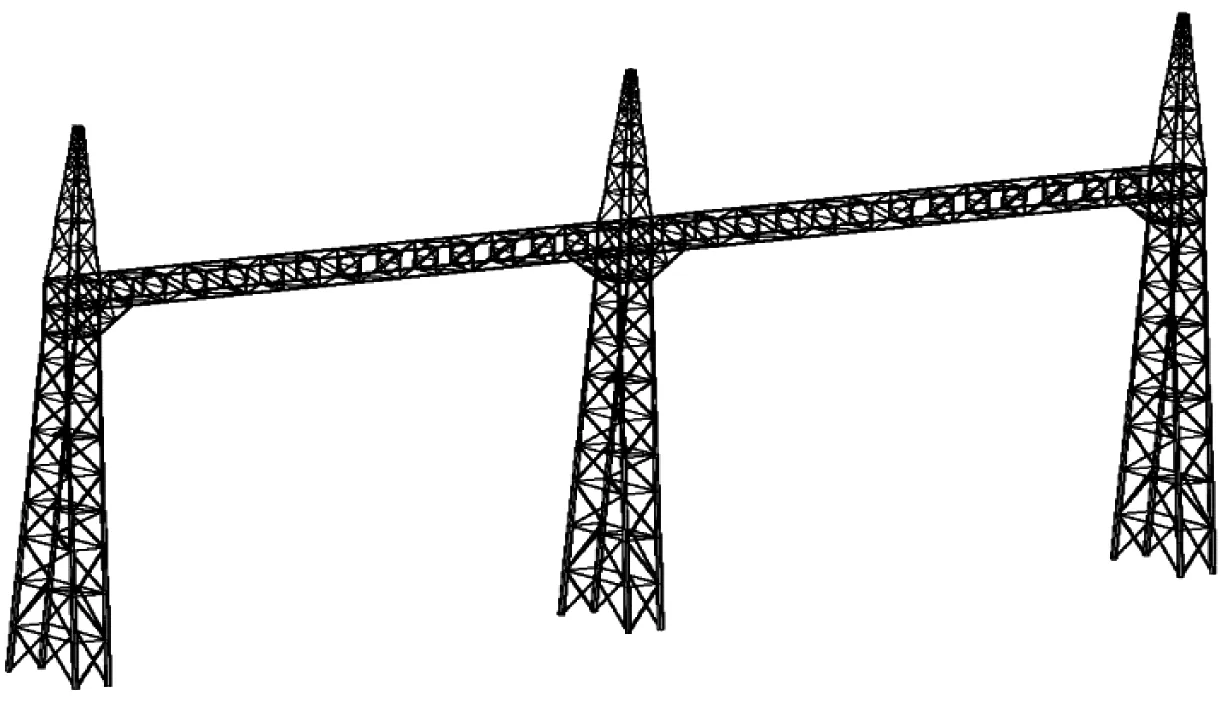
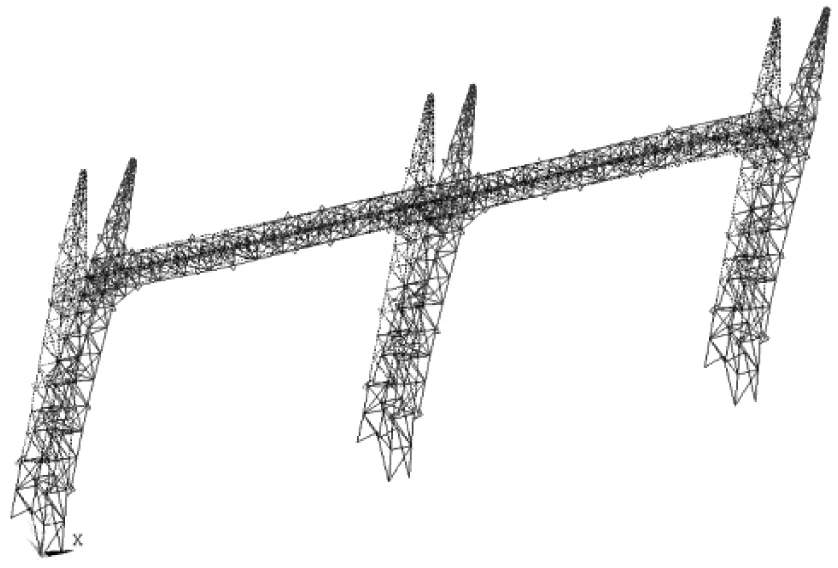
多跨格构式构架气弹模型以典型1 000 kV两跨变电构架为工程背景，原型如图1所示。该构架的跨数×跨度×高度=2×51 m×61 m，整体均为薄壁钢管构成。

图1 两跨变电构架原型

根据相似理论，气弹模型的设计除了需满足几何外形、刚度、质量相似以外，还要满足Strouhal数、Cauchy数、Froude数、Reynolds数和阻尼比等无量纲参数的相似。但在气弹模型实际设计制作过程中所有无量纲相似参数不可能同时满足。本文设计的气弹模型满足了Strouhal数、Cauchy数、Froude数和阻尼比的相似。对于钢管格构式构架结构，Reynolds数的影响不可忽略，主要表现为三分力系数。对于阻力系数，均匀流场内需要考虑Reynolds数效应的折减；紊流场中该系数随Reynolds数变化很小[26-28]。考虑到风洞试验在紊流场中进行，采用高密度流体或高风速满足Reynolds数相似十分困难，故设计气弹模型时放松对Reynolds数的要求，根据已有文献[29]，通过对试验结果进行修正来考虑Reynolds数的影响。

根据无量纲参数的要求，结合变电构架原型的结构高度，风洞试验段截面尺寸和模拟紊流边界层尺寸等要求，该气弹模型的几何缩尺比定为1/50。各主要相似参数如表1所示。

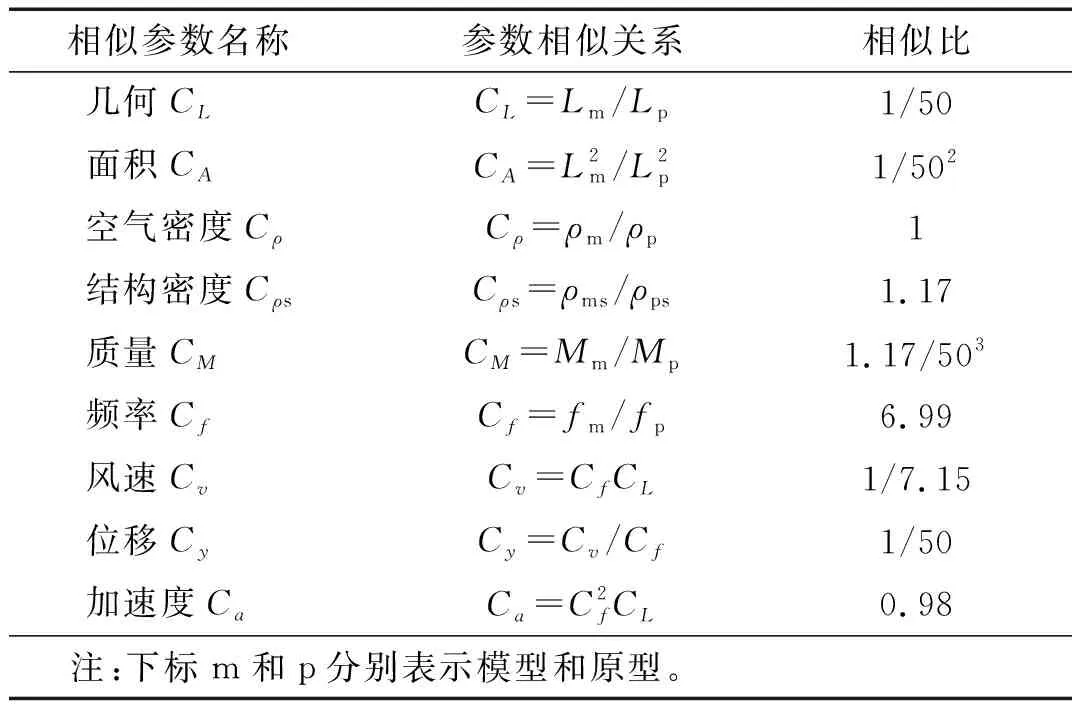
表1 气弹模型相似参数

完成对气弹模型的基本设计后，在气弹模型制作过程中，重点关注对几何外形、刚度、质量和阻尼比相似的模拟。

几何外形模拟是根据杆件截面尺寸，对构架杆件分类，并按几何相似比确定其对应气弹模型的杆件尺寸。部分杆件截面尺寸相差较小，在缩尺后的误差忽略不计，因而可以简化杆件截面种类。根据格构式构架的结构特点，将其分成21个典型节段。选用薄壁不锈钢管作为杆件，杆件间通过无铅锡焊连接，构成各刚性节段。

刚度相似模拟，即气弹模型的刚度由特制的V型弹簧片提供，即各节段通过V型弹簧片连接。弹簧片需要满足弯曲刚度和轴向刚度相似比的要求。其具体步骤为：运用ANSYS有限元软件建立构架原型的有限元模型，如图2(a)所示，分析其动力特性，根据相似比得到气弹模型的动力特性；建立加入V型弹簧片的气弹模型的有限元模型，如图2(b)所示；通过调节V型弹簧片的参数，包括厚度、宽度、及V型弯曲角度等，可得到满足相似比要求的有限元模型。由于弹簧片连接节段后会有一定的刚度损失，故在设计时需要考虑10%的富余刚度。最后，设计定型了3种规格的V型弹簧片，如图3所示。气弹模型使用的V型弹簧片材料均为弹簧钢，累计使用了136个弹簧片，其中1#弹簧片32个，2#弹簧片56个，3#弹簧片48个。弹簧片的受风面积占气弹模型总受风面积的比例，顺风向和横风向均在2%以内。

(a) 原型有限元

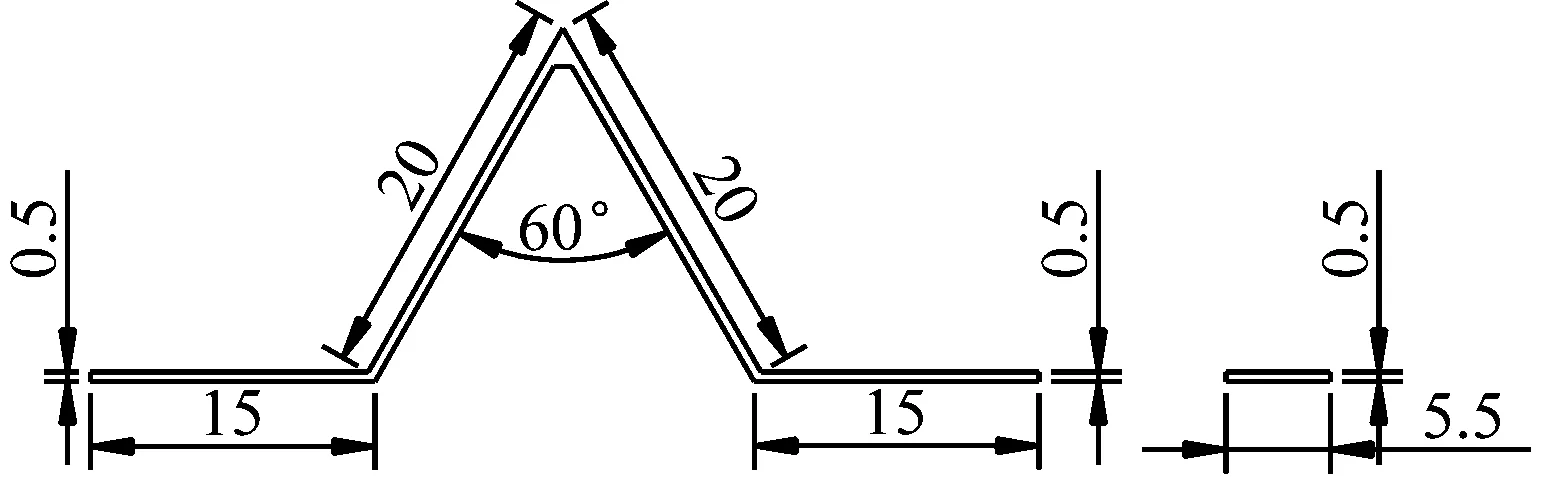
1#弹簧片

质量相似模拟，即气弹模型的质量分布应与原型一致，满足质量相似比，以确保动力特性的相似性。在设计气弹模型时考虑弹簧片的质量。在实际制作过程中，本次模型制作各节段质量与预期质量稍大，但是总体较接近，因此直接采用此质量。

阻尼比相似模拟。一般情况下，除了已知的材料特性外，设计阶段格构式构架气弹模型的阻尼比难以控制，只能在制作时注意尽量加固各个杆件的连接，减少杆件之间的摩擦，通过对气弹模型模态测试来检验阻尼比是否满足要求。由于刚性节段加V型弹簧片法的弹簧片与刚性节段连接简单，耗能部位少，对于模拟低阻尼比结构能够取得良好的效果。

1.2 气弹模型动力特性

在多跨格构式构架气弹模型制作完成后，为了检验模型的自振频率，需要对模型进行动力标定试验。如不符合动力特性要求，则需调整模型。本文由自由振动法得到气弹模型的自振衰减曲线，通过信号分析得到气弹模型前4阶频率、前2阶阻尼比，如表2所示。由表可知，气弹模型的主要模态频率与理论值较为吻合，相对误差在3%以内。同时，结构阻尼比的模拟效果较好，能够满足气弹模型风洞试验的要求。气弹模型前4阶模态的振型如表2和图4所示。图5为定型完成的多跨格构式构架气弹模型。

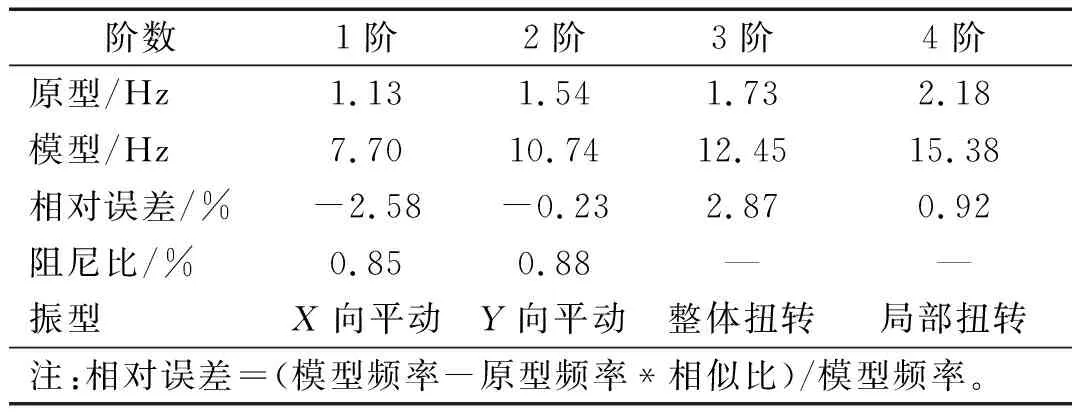
表2 气弹模型模态分析结果

1阶

图5 多跨格构式构架气弹模型

2 风洞试验

气弹模型风洞试验在武汉大学WD-1风洞试验室进行。该风洞试验段长×宽×高=16 m×3.2 m×2.1 m，最大风速为30 m/s，试验风速由1 m/s～30 m/s连续可调。直径2.5 m的自动控制工作转盘可以模拟0°～360°任一风向角的模型试验风场。

2.1 风场模拟

风洞试验采用档板、尖塔、粗糙元等装置来模拟大气边界层风场。由于构架原型所在地为濒海地区，其地势较为平坦，根据现场情况及对地貌形式的考虑，本文风洞试验模拟B类地貌。B类地貌的风剖面、紊流度如图6所示，风速谱为Von Karman谱，如图7所示。

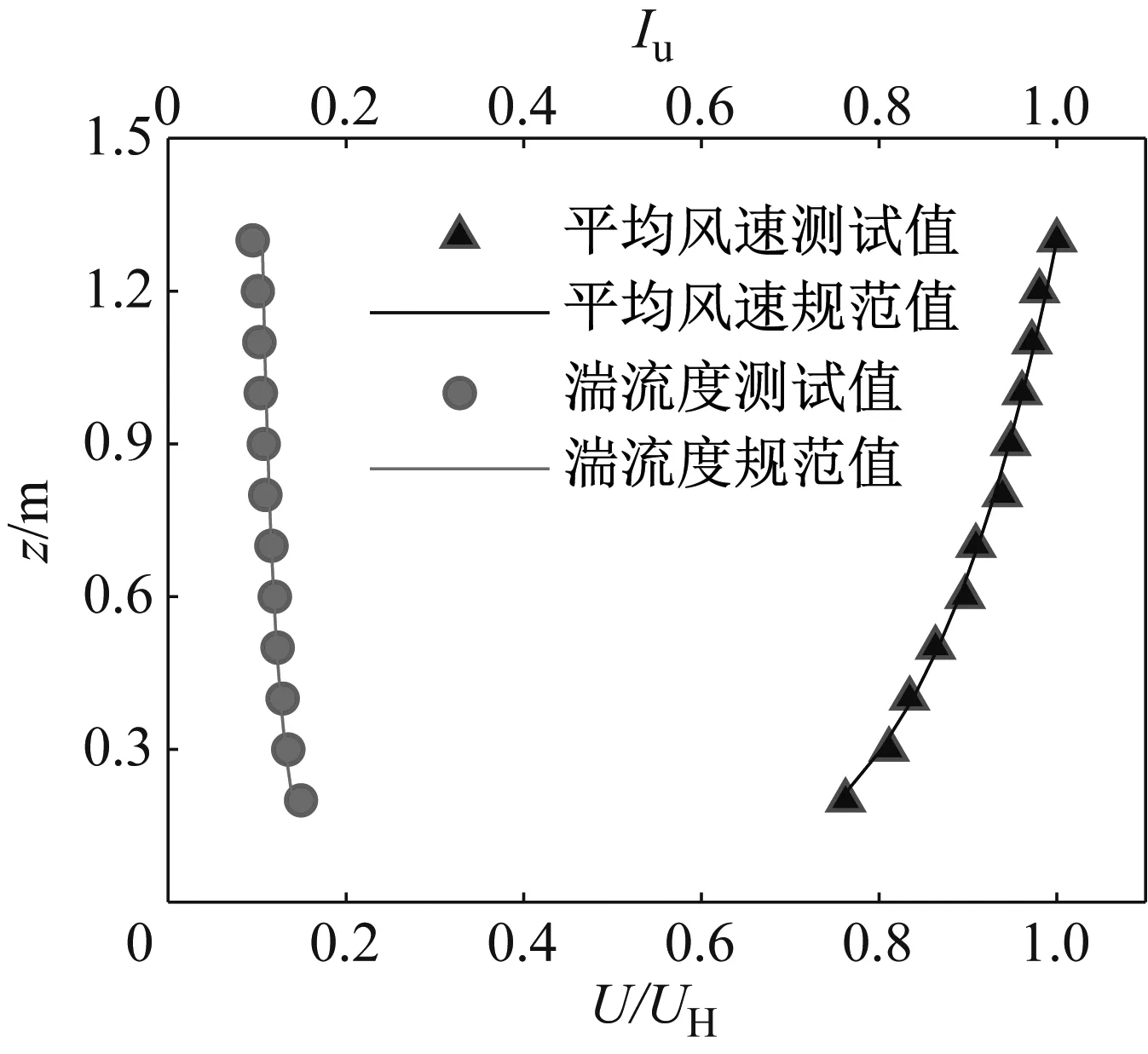
图6 平均风速与紊流度剖面

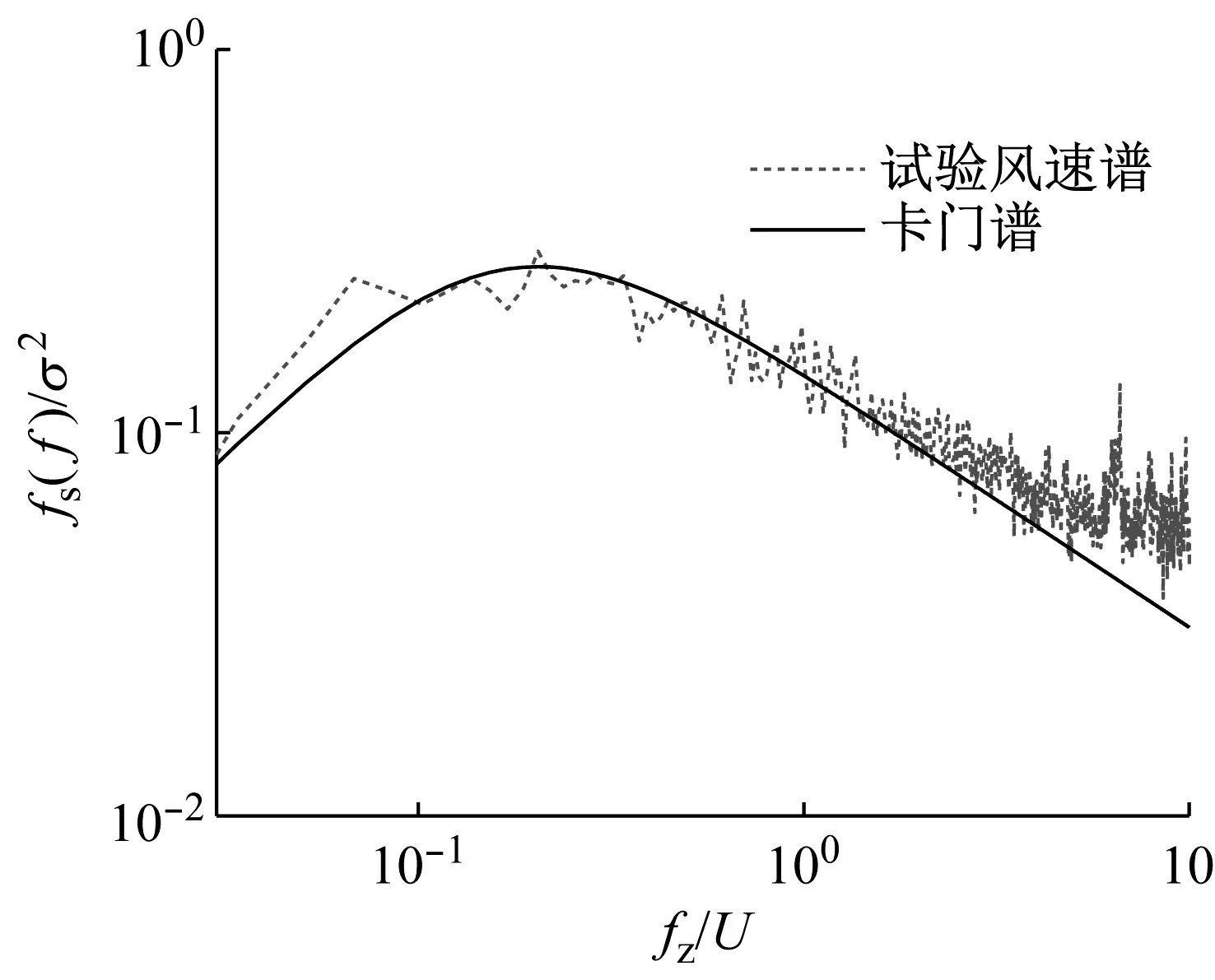
图7 脉动风功率谱

2.2 试验方法

试验通过旋转工作转盘，模拟-90°～90°风向角的情况，各风向角角度间隔为15°，共13个试验风向角。试验风速为3 m/s，4 m/s，5 m/s，6 m/s，8 m/s，共5个风速。眼镜蛇风速仪安装高度为气弹模型顶部高度1.22 m。采样时间为90 s，其中，激光位移计采样频率为500 Hz，加速度传感器采样频率为512 Hz。风洞试验如图8所示，风向角与结构轴向定义如图9所示。为了研究气弹模型的风振响应特性，分别测试Y轴向中塔、边塔顶部(定义为Y1、Y2)，中塔、边塔中部横梁连接处(定义为Y3、Y4)，边塔顶部、中部横梁连接处(定义为X1、X2)共6处典型节段的位移与加速度，如图10所示。

图8 气弹模型风洞试验

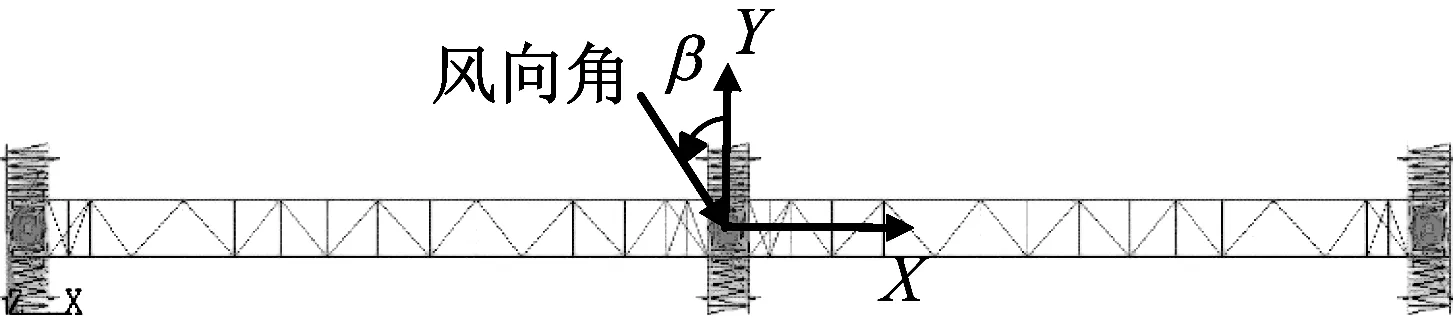
图9 风向角与结构轴向

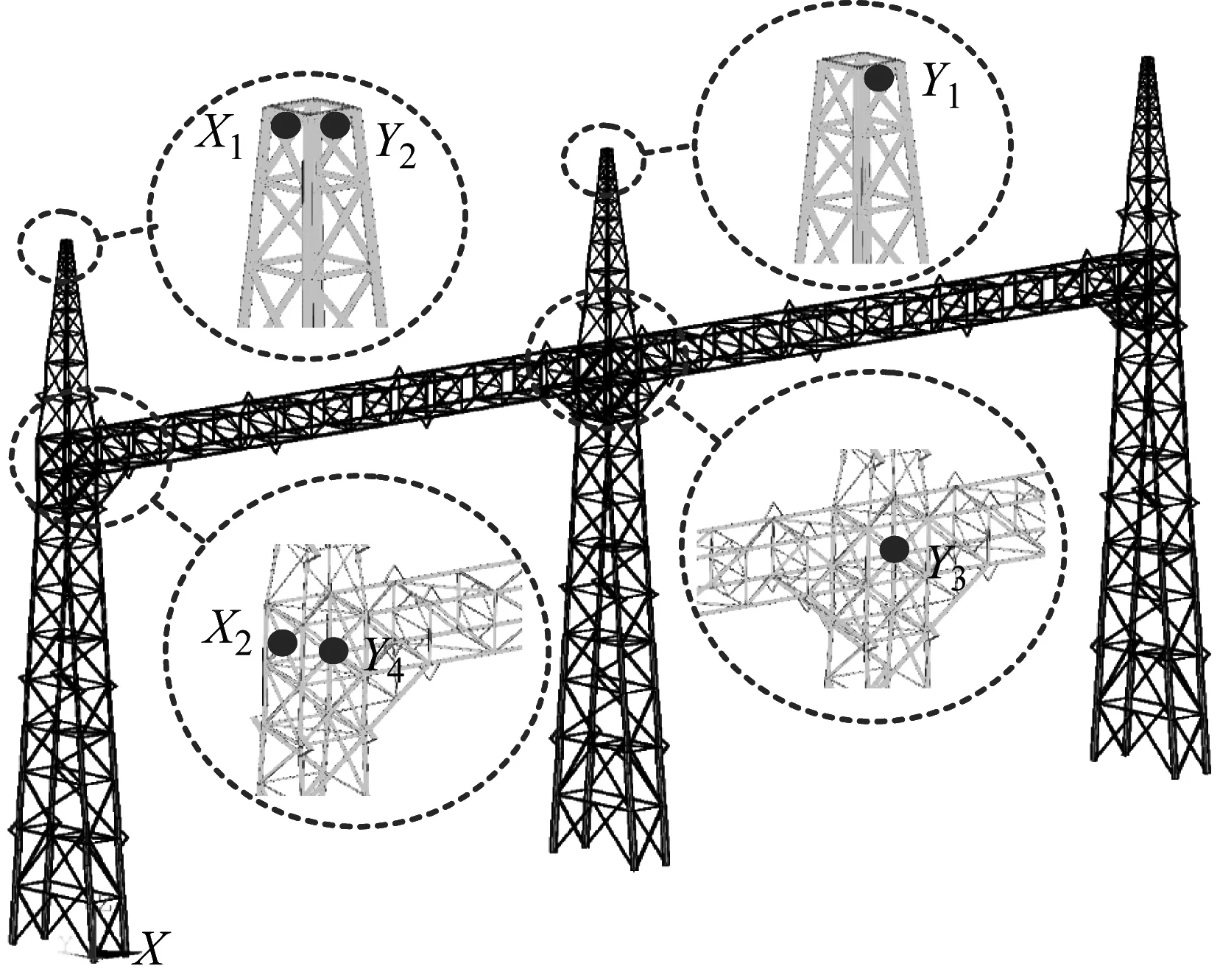
Y轴向：Y1、Y2、Y3、Y4；X轴向：X1、X2

3 试验结果分析

试验测试了不同工况下1 000 kV变电构架气弹模型典型节段的位移、加速度响应时程。根据统计方法得到了位移响应均值、均方根值，加速度响应均值、均方根值。

3.1 位移响应

各测点位移均值在-90°，0°和90°风向角下随风速的变化曲线如图11所示。由图11可以得到：顺风向的位移响应平均值随风速增大而增大。0°风向角下，中塔(Y1、Y3测点)顺风向位移均值要大于同一高度边塔(Y2、Y4测点)位移均值。横风向的位移均值随风速增大变化幅度较小，其值接近于0。

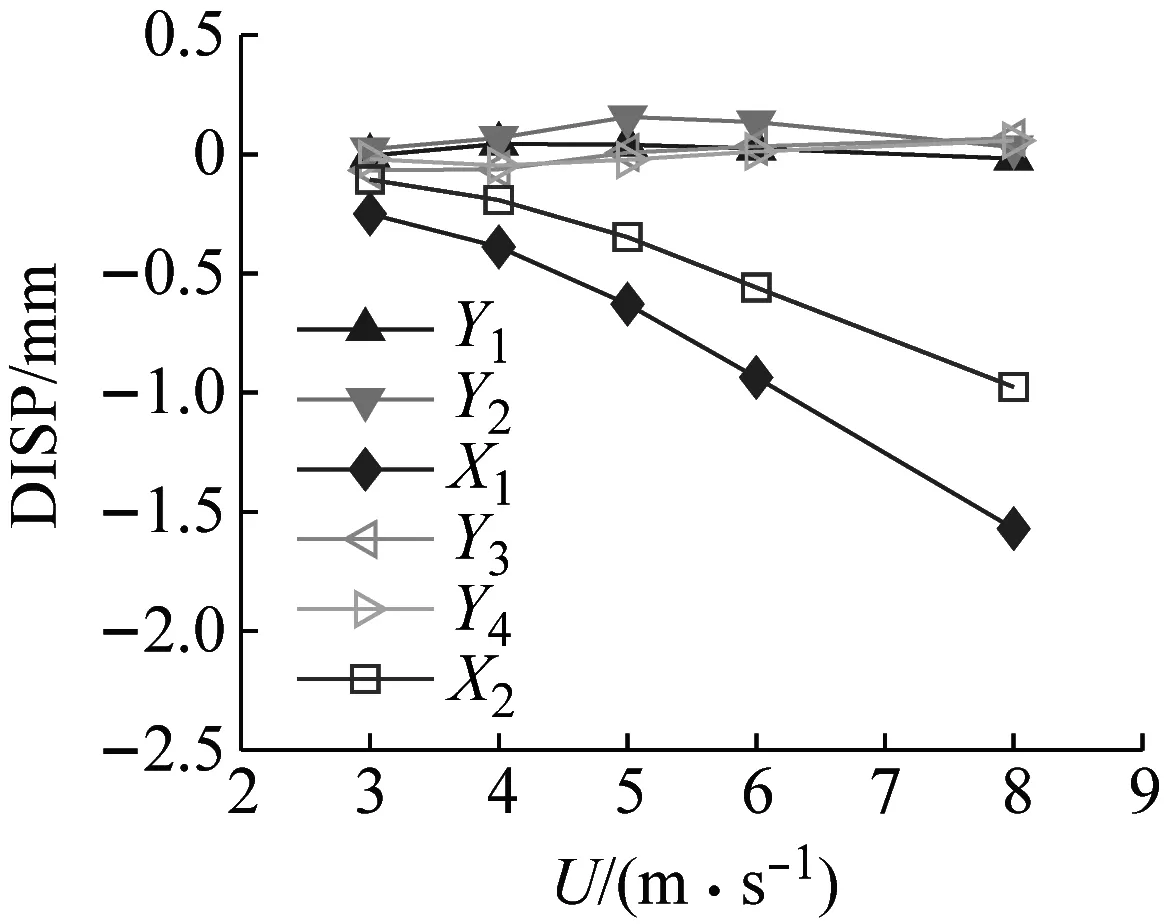
(a) -90°风向角位移均值

图12为Y1、Y2、X1测点，位移均值随风向角的变化曲线。由图可以得到：对于Y轴向，中塔顶部(Y1测点)和边塔顶部(Y2测点)位移均值随风向角的变化规律基本相同。在-90°～0°风向角，Y向位移响应从0左右不断增大，在75°时达到最大值。在0°～90°风向角，Y向位移响应的变化规律与-90°～0°的相似，即关于0°对称，在15°达到最大值。对于X轴向，边塔顶部位移响应的变化规律关于0°风向角同样有一定的对称性，即在-75°或75°达到最大值。其主要原因是在-15°或15°时，构架正面的迎风面积较大，在-75°或75°时，构架侧面的迎风面积较大。总体来看，位移均值随风向角的变化较为敏感。Y轴向同一高度，中塔顶部(Y1测点)的位移均值稍大于边塔顶部(Y2测点)；X轴向的位移响应最大值大于Y轴向的位移响应最大值。

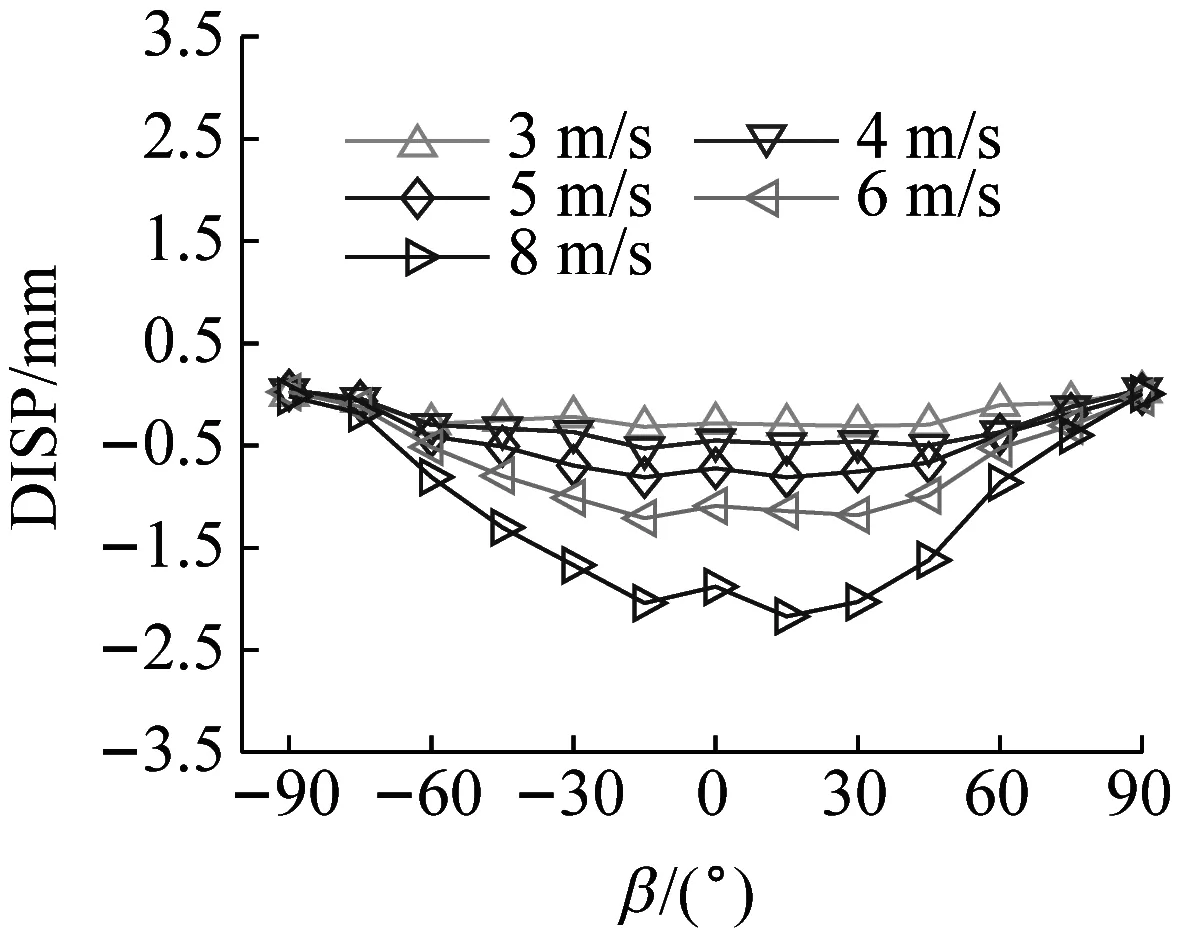
(a) Y1测点位移均值

3.2 加速度响应

图13为-90°，0°，90°风向角下，不同测点加速度响应均方根值(root mean square of acceleration, RMSA)随风速变化的曲线。由图13可以看出，各测点加速度响应均方根随风速增大而单调增加。同一高度处，中塔(Y1、Y3测点)加速度响应均方根与边塔(Y2、Y4测点)较为接近。对于同一塔柱，中部横梁连接处加速度响应均方根明显小于顶部，约为顶部的40%～60%。

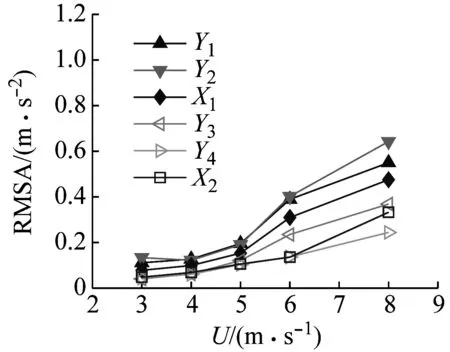
(a) -90°风向角加速度均方根

图14为Y1、Y2、X1测点加速度响应均方根值随风向角变化的曲线。由图可以得到，除少数工况外，加速度响应均方根随风向角的变化不明显，基本维持在某个值附近。在-90°～0°风向角，加速度响应均方根有略微增大的趋势。而0°～90°风向角的变化规律与-90°～0°风向角相近，关于0°有一定的对称性。在大多数工况下，构架边塔Y向(Y1测点)的加速度响应均方根大于边塔X向(X1测点)的加速度响应均方根。

由图13和图14可以得到，0°风向角下，顺风向和横风向的加速度响应均方根同一数量级，横风向风致振动效应不可忽略。主要原因是该结构的横风向1阶频率为1.13 Hz，顺风向1阶频率为1.54 Hz，即横风向刚度小于顺风向刚度。此外，该结构为两跨三塔结构，各塔的横截面为矩形，各塔的横风向受风面积大于顺风向，总体而言，结构总的横风向受风面积与顺风向相比，相差不大。因此，横风向风致振动效应较为明显。

由于构架气弹模型顶部风振响应最大，将气弹模型顶部加速度响应时程通过傅里叶变换得到功率谱密度，并进行谱分析。图15为0°风向角，变电构架顶部(Y1、Y2和X1测点)典型工况，加速度响应功率谱密度。由图可得：在Y轴向，中塔顶部(Y1测点)的加速度响应以该方向第1阶模态的共振分量为主，高阶模态贡献较小；对于边塔顶部(Y2测点)的加速度响应，该方向前3阶模态的共振分量均较大，高阶振型的贡献不可忽略。在X轴向，边塔顶部加速度响应由该方向第1阶振型共振分量构成。

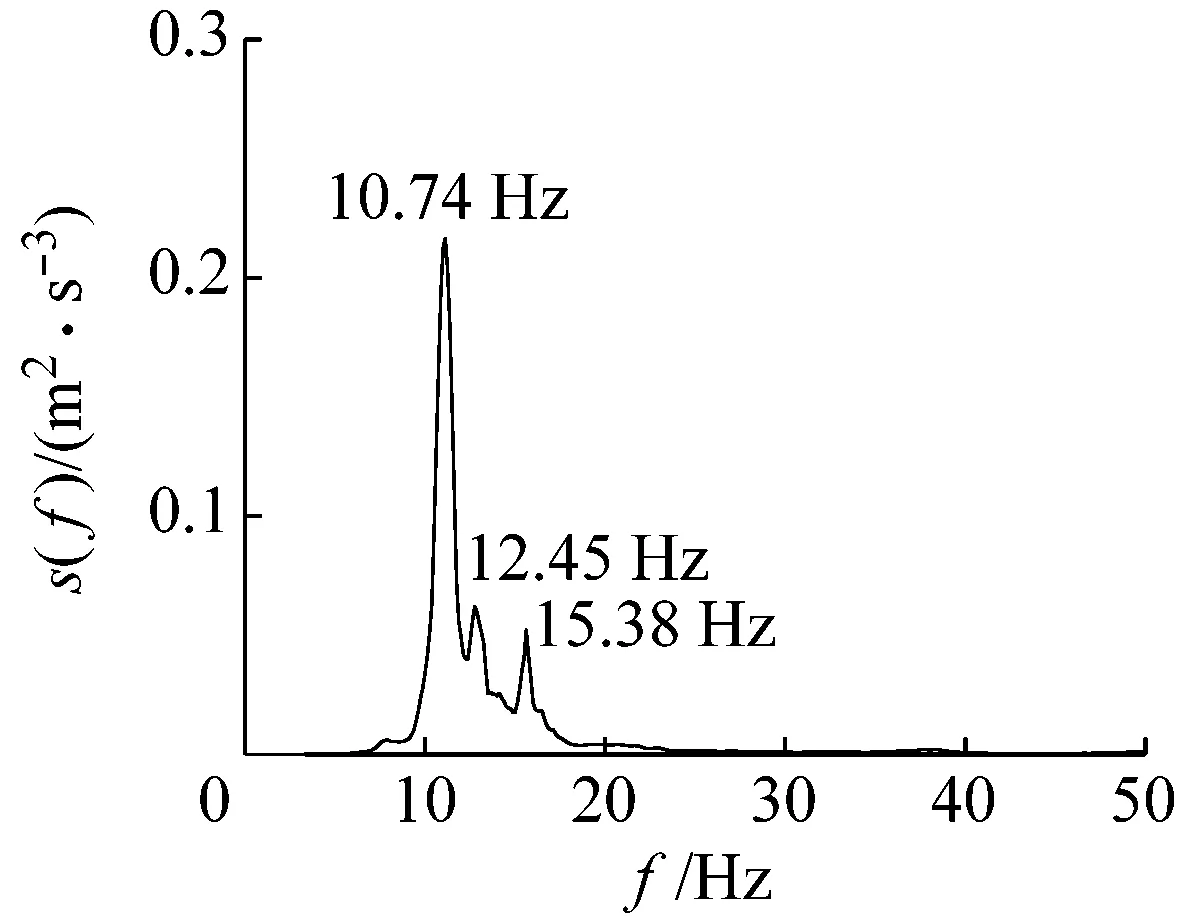
(a) Y1测点加速度响应功率谱

3.3 风振系数

风振系数是将动力风荷载根据一定原则简化为静力作用，对工程设计十分重要。与独立格构式高耸结构不同，各类规范中对多跨格构式构架，尤其是1 000 kV变电构架结构的风振系数取值并不明确。在对复杂多跨格构式构架设计时，常结合工程经验，对风振系数进行取值。因此，根据气弹模型风洞试验，直接测得风振响应，计算多跨格构式构架典型节段的风振系数，有一定的设计参考价值。本文主要采用惯性风荷载方法和阵风荷载因子方法计算风振系数。其中，惯性力风振系数βL(z)的计算见式(1)，位移风振系数βD(z)的计算见式(2)

(1)

式中:g为峰值因子，本文取3.5；M(z)为z高度处的集中质量；σa(z)为顺风向加速度响应的均方根值；μs(z)为z高度处体型系数，根据文献[30]选取；μz(z)为z高度处风压高度变化系数，w0为基本风压，A(z)为z高度处杆件投影面积。

(2)

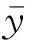
表3为风振系数的计算结果。可以看到，惯性力风振系数βL(z)的取值在1.35～1.58，位移风振系数βD(z)的取值在1.40～1.59，两者的取值范围较为接近。同一风向角下，同一节段的βL(z)要略小于βD(z)，可能是由于βL(z)只考虑了共振分量的贡献，而βD(z)包含了共振分量和背景分量，采用βD(z)值作为设计参考值更为合适。

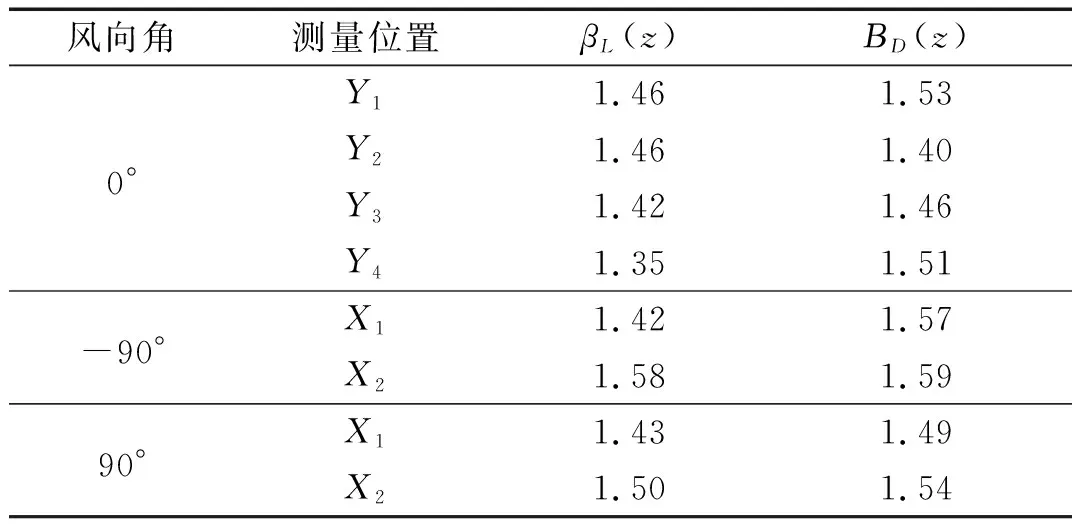
表3 风振系数

4 结 论

以1 000 kV变电站内典型两跨变电构架为背景，基于刚性节段加V型弹簧片法设计制作多跨格构式构架气弹模型，进行风洞试验，研究该类结构风振响应与风振系数特点。得出主要结论如下：

(1) 本文设计制作的多跨格构式构架气弹模型前4阶模态的频率与模型分析结果吻合较好。对于此类结构，以刚性节段加V型弹簧片法设计气弹模型可以避免离散刚度法的材料刚度不足和阻尼比偏大的问题。同时，该方法相对于集中刚度法，也能更精确地反映多跨格构式构架的风振响应特性，是一种较为合适的设计方法。

(2) 多跨格构式构架顺风向的位移响应平均值随风速增大而明显增大。横风向的位移均值随风速增大变化幅度较小，其值接近于0。风向角对位移均值的影响十分显著。最不利风向角与相应主轴成15°夹角，应重视该风向角的抗风设计。

(3) 该类结构顺风向与横风向的加速度响应均方根处于同一数量级，横风向风致振动效应较为明显，在设计时应考虑横风向振动。同一高度处，中塔加速度响应均方根与边塔较为接近。对于同一塔柱，中部横梁连接处加速度响应均方根明显小于顶部，约为顶部的40%～60%。

(4) 从加速度响应的频谱图可以得到，多跨格构式构架结构垂直于跨向(Y轴向)中塔的加速度响应以该方向第1阶模态的共振分量为主，高阶模态的影响较小。对于边塔的加速度响应，高阶振型的贡献不可忽略。在跨向(X轴向)，该结构加速度响应由该方向第1阶振型共振分量构成。

(5) 同一节段的位移风振系数值略大于惯性力风振系数值，两种风振系数值均在1.3～1.6，建议采用位移风振系数值作为设计参考值更为合适。