电动汽车用永磁同步磁阻电机电感测试方法

王世伟，韩雪岩，李宏浩

(沈阳工业大学 国家稀土永磁电机工程技术研究中心，沈阳 110870)

0 引 言

永磁同步磁阻电机兼具永磁电机和磁阻电机的优点，具有高功率密度、高效率及较宽的调速区间，在电动汽车驱动中获得了广泛的应用[1-3]。

永磁同步磁阻电机的交、直轴电抗决定了系统性能的优劣，不同的d、q轴电抗值和不同的凸极率，对电机的弱磁性能和外特性产生主要影响，是电机设计的关键参数之一[4-5]。电动汽车用电机主要采用最大转矩电流比(maximum torque per ampere,MTPA)控制，在开环情况下，参数不匹配对整个系统性能有很大影响[6-7]。电机的交轴和直轴电感随坐标轴平面上电流矢量的大小和角度而产生非线性变化。在永磁同步磁阻电机的参数中，由于磁路的饱和效应和磁钢b-h曲线的非线性，给直、交轴电感的准确计算和测试带来很大难度[8]。

基于电抗参数对电机性能的重要影响，许多学者对电抗参数的测试方法进行了大量研究[9-11]。文献[12]中固定转子位置，并使用矢量控制器产生一个逐步变化的交/直轴电压，保持直/交轴电流保持不变。根据电流响应，计算交、直轴电感。这种方法的难点在于产生逐步变化的d轴或q轴电压。在普通的三相逆变器中，不能直接从脉宽调制电压中获得。必须使用高精确度低通滤波器。文献[13]研究不同转子结构下交叉饱和对电枢反应电抗的影响规律，并分析了产生这种影响的原因，但并未提出实际的测试方法。文献[14]介绍了采用伏安法测试电枢反应电抗，伏安法多在伺服电机电感测试中使用，但测试永磁同步磁阻电机电抗时，由于隔磁桥的存在，测试过程中电感变化很小，很难确定交直轴位置，而且没有考虑交叉磁化效应的影响。还有许多学者采用有限元分析计算电机的电感参数，但其计算受材料、加工工艺以及控制策略的影响较大，以致计算值与实际值有一定的偏差。

本文根据目前电抗参数测试出现的问题，提出了静态测试和动态测试两种不同的电感测试方法。静态测试基于静止参照系中交、直轴电压方程式，通过测试三相电压和电流，可以计算出不同电流大小和矢量角下的d、q轴电感。动态测试方法基于功率分析仪、转变解码器等现代检测设备，在电机运行工作域内，实时测试电机不同工况下的电感值。两种测试参数方法应用到一台20 kW电动汽车用电机控制器上，与试验室经常采用的高频电源伏安法测试参数相比较，控制性能明显提高。

1 电感测量原理

1.1 静态参照系中的电感测试原理

静止参照系中永磁同步磁阻电机的电压方程如下[15]：

(1)

其中：

Lβ=L+ΔLcos(2θs)；Lα=L-ΔLcos(2θs)；

Lαβ=ΔLsin(2θs)。

式中：rs为相电阻；ψf为永磁体的磁链；p为d/dt算子；θs为静止坐标系中的转子位置。其中L和ΔL的计算公式如下：

(2)

其中Lq和Ld是旋转参考坐标系的交轴和直轴电感。将静止坐标系下，电压基本方程式(1)展开得到如下方程：

2ωΔLcos(2θs)Iα+ωψfcosθs；

2ωΔLcos(2θs)Iβ-ωψfsinθs。

其中与ω相关的变量可以在静止状态下消除，为了消除正弦和余弦相关相，将转子位置角θ设置为0(或90°)。因此，方程式可简化为：

(3)

其中Uα、Uβ、Iα和Iβ分别是直轴和交轴的电压和电流，通过轴系的坐标变换，可以采用直接测量的3相电压和3相电流来表示。在测试中，考虑到采样数据，将式(3)修改为

[2Ua(k)-Ub(k)-Uc(k)]=

rs[2Ia(k)-Ib(k)-Ic(k)]+

[Uc(k)-Ub(k)]=rs[Ic(k)-Ib(k)]+

(4)

其中：k为数据的第k个值；Ts为测量设备的采样周期。最后，为了表示电感与电流矢量之间的关系，需要将三相电流通过Park变换转换为旋转坐标系中矢量的大小和角度，即

(5)

如式(5)所示，Is为电流矢量的大小，β为电流矢量与交轴的夹角。θs角可从0°开始变化，交轴和直轴电流也可从小到大变化。因此，按照此方法测试的交轴和直轴电感可以涵盖各种电流矢量状态，它们的饱和状态可以通过不同的电流大小来反映，它们交叉影响，也可以通过不同电流矢量角的变化来测量。

1.2 动态电感测试原理

假设如下:

1)磁通在定子和转子之间以正弦波的形式分布;

2)电压和电流的谐波分量忽略不计;

3)忽略铁耗;

4)忽略永磁体性能变化。

在d-q轴坐标系上表示的永磁同步磁阻电机电压方程为

(6)

其中：Ud和Uq分别为每相电枢电压的直轴和交轴分量；R为每相电枢绕组的阻值；p为微分算子；Ld和Lq为直轴和交轴的自感；ω为转向角(电角)速度；φa(=Ke)为永磁体交链电枢绕组的有效值(感应电压常数)。

假设为稳定状态(即忽略时间导数项)，d轴和q轴的矢量图如图1所示。图中：U和i分别表示相电压和相电流的基波分量；θu和θi分别表示电压和电流基波对应于q轴的夹角。基于图1所示，交、直轴电压方程表达式为：

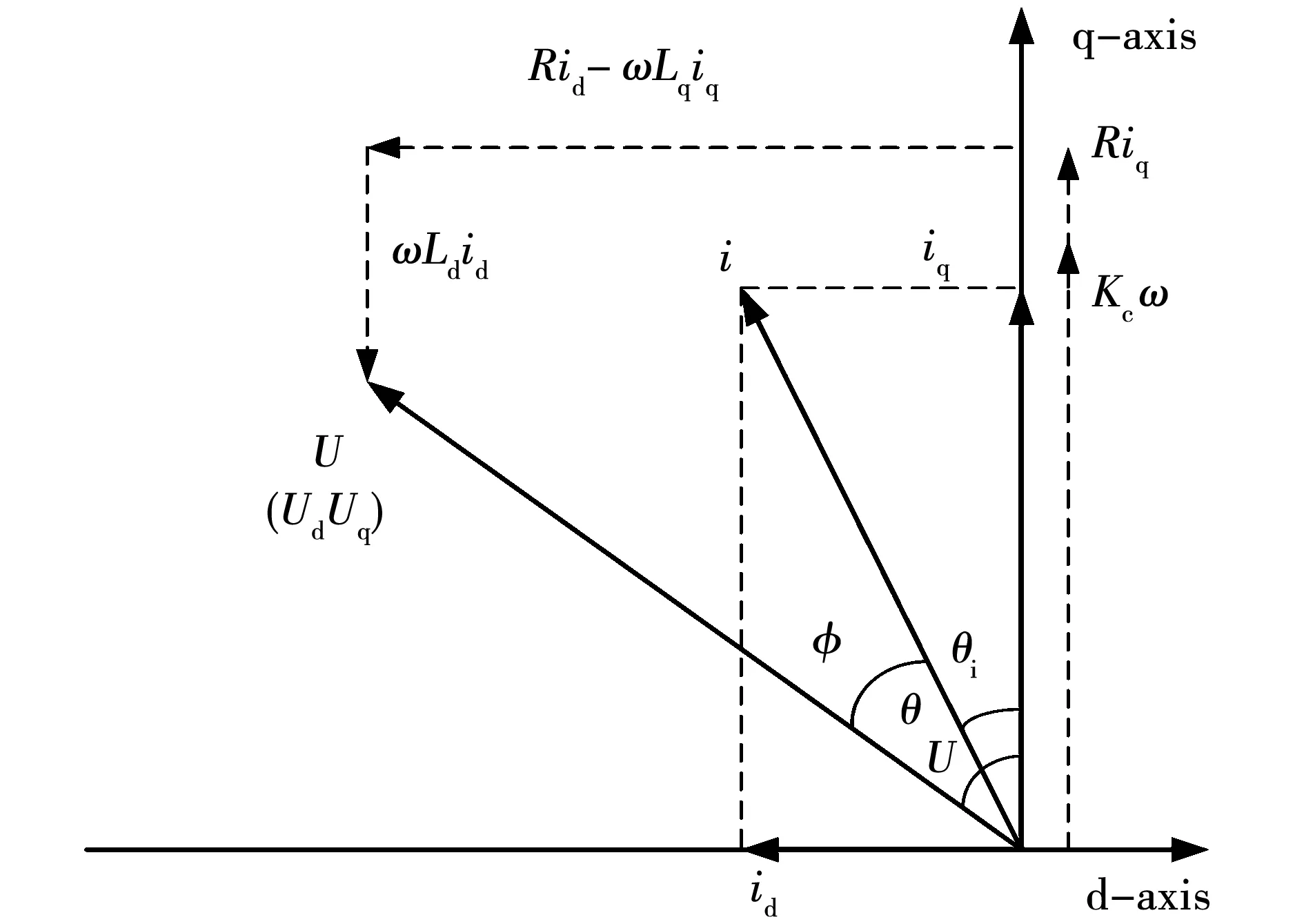
图1 d-q轴电压矢量图Fig.1 Voltage vector diagram of d-axis and q-axis

Keω+RIq=Uq-ωLdId；

(7)

Ud=RId-ωLqIq。

(8)

进而得到Ld和Lq的求解方程：

(9)

(10)

按照图2所示，对三相绕组施加适当直流电，转子在电磁力的作用下，锁定转子交轴方向和A相轴线重合。电动车用永磁同步磁阻电机通过旋转变压器进行位置控制，因此可以通过采用解码芯片读取旋转变压器的信号，进而获得被试电机转子初始位置，然后对旋转变压器进行相位调零。

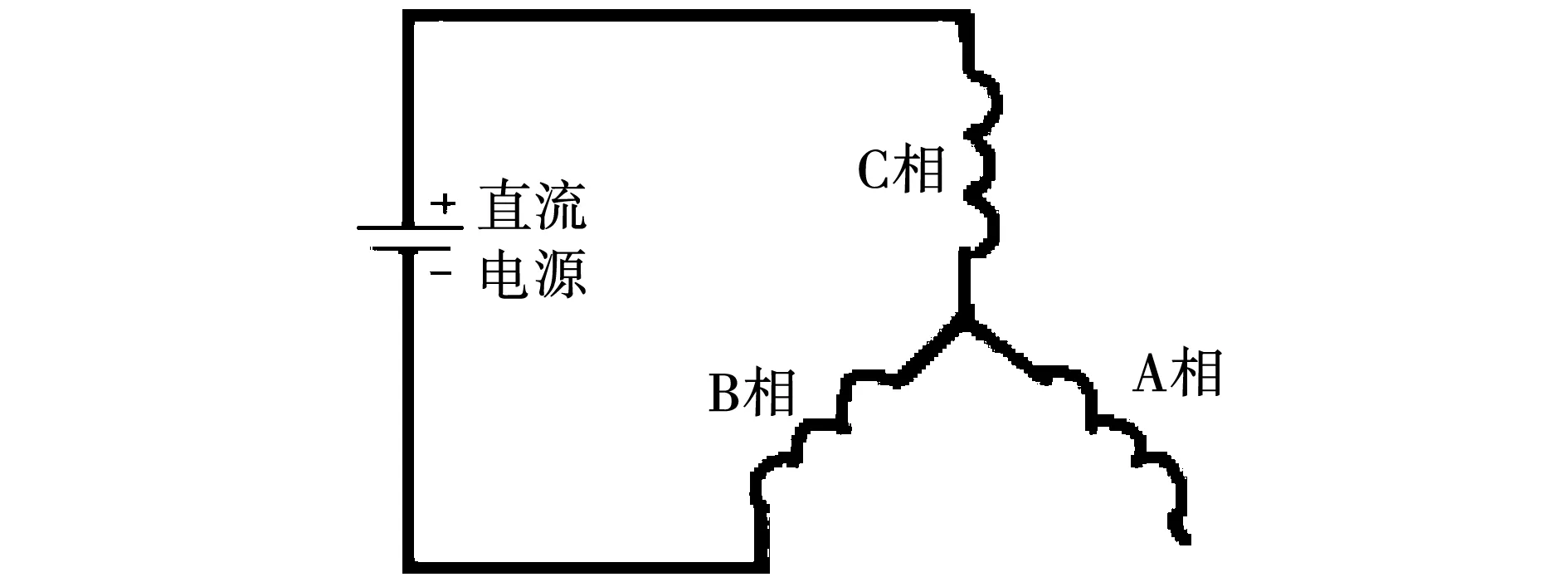
图2 直流通电示意图Fig.2 Schematic diagram of direct current

当把被试电机当做发电机运行时，由负载电机拖动被试电机运行，被试电机处于发电机空载运行状态，此时端电压U即为空载感应电势，因此由能够识别ke，即

(11)

式中f(=ω/2π)表示相电压基波频率。

采用数字电阻测量仪可以获得电机定子绕组值R，通过对旋转变压器位置调零，在电机运行过程中满足：

Ud=-Usinθu；

(12)

Uq=-Ucosθu；

(13)

Id=-Isinθi；

(14)

Iq=-Icosθi。

(15)

进而通过式(9)和式(10)计算得到不同工作状态下的交轴和直轴的电感值

2 试验

2.1 被试样机

采用上节提到的静态测试和动态测试两种电感测试方法，对一台20 kW车用永磁同步磁阻电机进行了实验验证。图3为被试样机定子、转子和整机图片，表1为样机基本参数。

图3 被试样机Fig.3 Tested motor

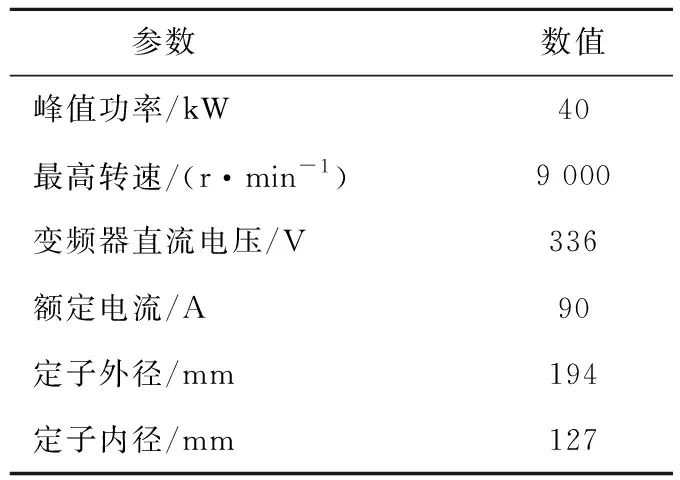
表1 被试样机基本参数

2.2 静态试验及数据处理

2.2.1 静态试验

根据电感计算推导的计算方程，静态测试电机电感需要理想的三相交流电压源(或电流源)，将采用电压源。在静止状态下，每一相都没有反电动势，非常低的电压激励便可以让电机绕组达到额定相电流。因此，选择电压源时应优先选择低压量程的，以提高测试精确度。等效铁损电阻随着源频率的增加而增大，因此电压源需要谐波含量尽量低。如式(4)所述，总共有6个变量需要测量。由于三相电感分布不对称，电机中性线上存在电压分量，即三相电压之和不再为零，但三相电流之和始终为零。因此，在测试Lq时需要测量三相电压和一相电流，测试Ld时，需要测量两相电压和两相电流。通过对绕组通入直流电流，找到转子的零位置。实验设置如图4所示，整个实验装置包括一个三相交流电源、一个4通道示波器、两个副栅钳。

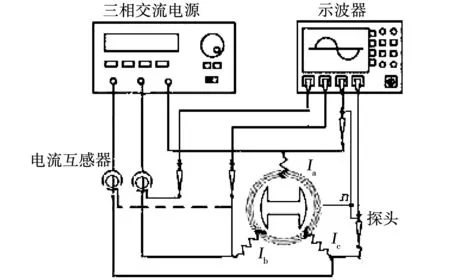
图4 静态电感测试方案Fig.4 Static measurement scheme for inductance

2.2.2 静态测试试验数据处理及计算

如图5和图6中的波形是用数字示波器测量的存储波形。图5是用于计算直轴电感的测试波形，图6是用于计算交轴电感的测试波形。

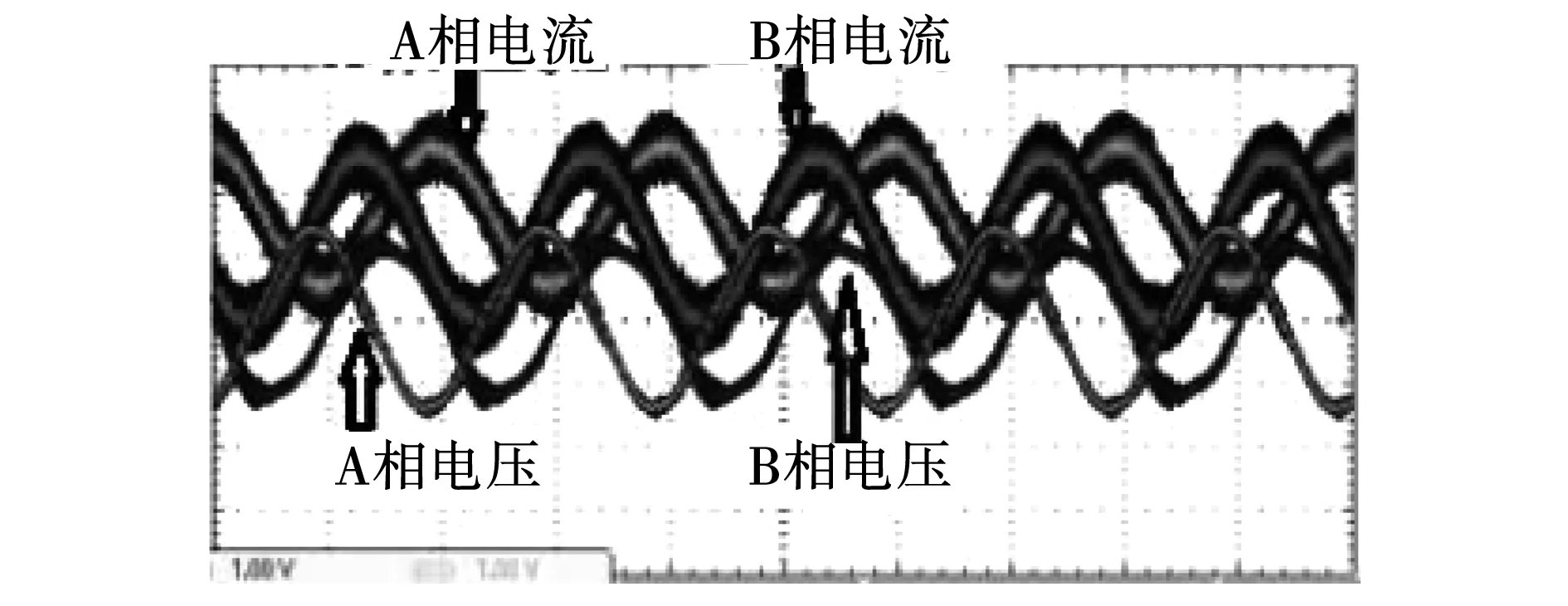
图5 两相电压、两相电流测试波形Fig.5 Test waveforms of two-phase voltage and current

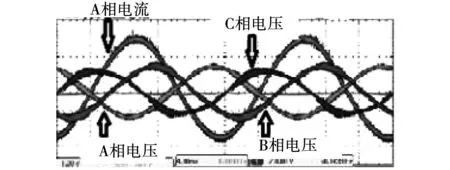
图6 三相电压、一相电流测试波形Fig.6 Test waveform of three-phase voltage and one-phasex current

测量的电压和电流是离散时间数据。很明显，在被测波形中存在大量的噪声，因此数据不能直接使用。通过快速傅立叶变换滤波器，可以从原始实验数据中去除频率高于式(6)中频率的傅立叶分量，即

(16)

其中:n是一次考虑的数据点数量；ΔT是两个相邻数据点之间的横坐标时间间距。图7显示了A相电压的原始数据和滤波波形之间的比较。

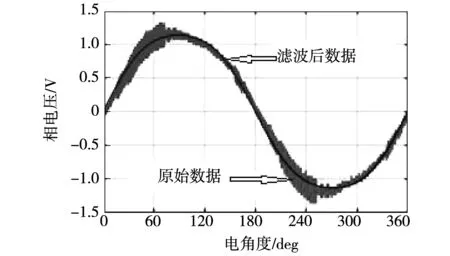
图7 相电压波形原始数据和滤波数据的比较Fig.7 Comparison of the original data and thefiltered data of phase voltage waveform

图8显示了用测量的相电压和电流计算的原始电感。可以看出，原始电感的结果有一些波纹。主要原因是定子的槽和齿在空间分布上产生不同的磁导率。此外，由于电路不对称，电流大小和矢量角的变化也会产生不同的饱和和交叉磁化效应。为了消除计算电感的纹波， 采用多项式最小二乘函数拟合曲线，一般的k阶多项式最小二乘函数如下：

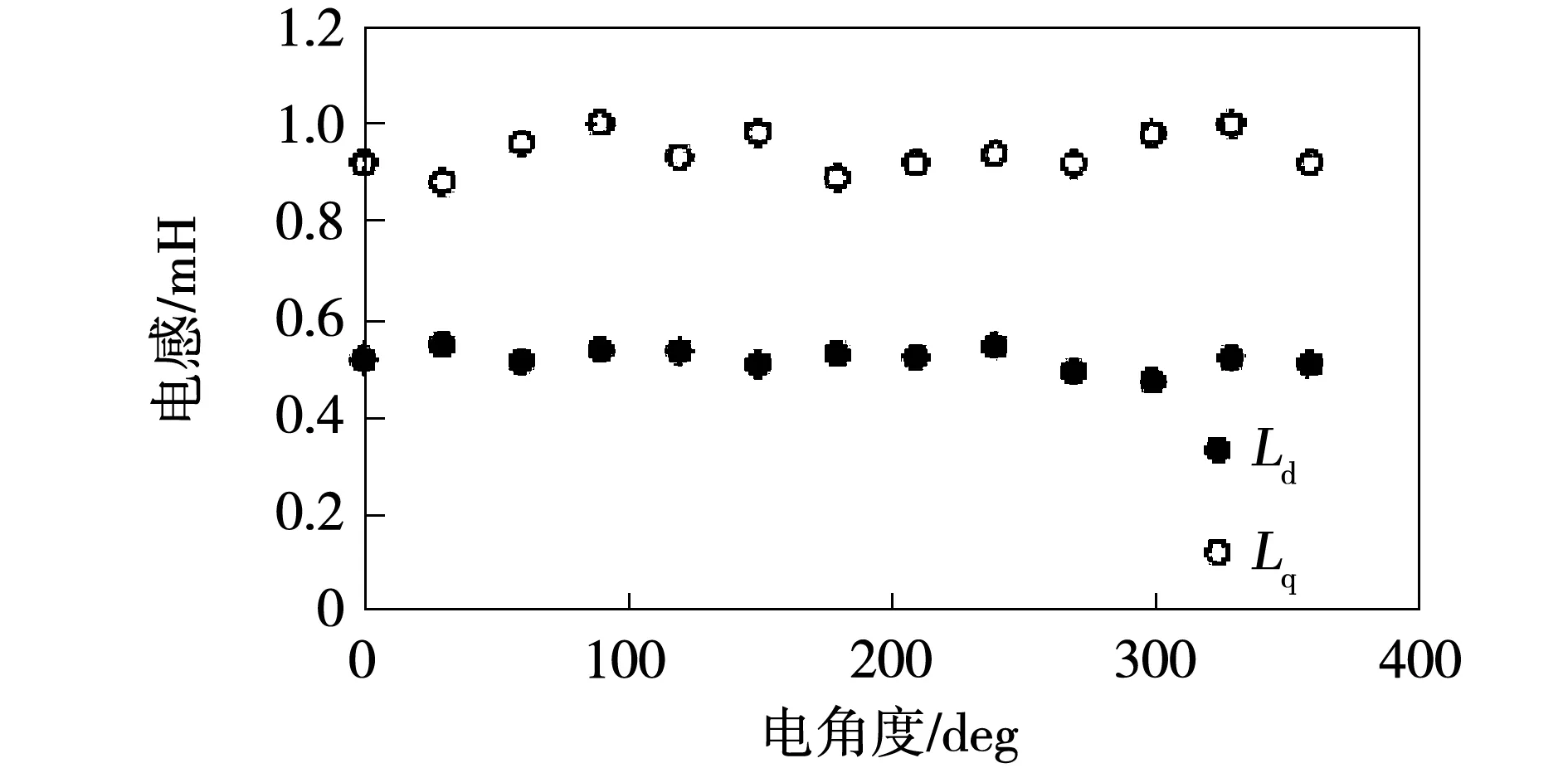
图8 在一定电压下测得的原始d轴和q轴电感Fig.8 Raw measured d-and q-axis inductancesat certain voltage

f(x)=a0+a1x+a2x2+…+akxk；

(17)

(18)

其中σi是第i个数据的测量误差。

数据通过曲线拟合处理后计算结果如图9所示。采用静态测试方法在相同电流矢量角情况下改变电流幅值,测试结果如图10所示。

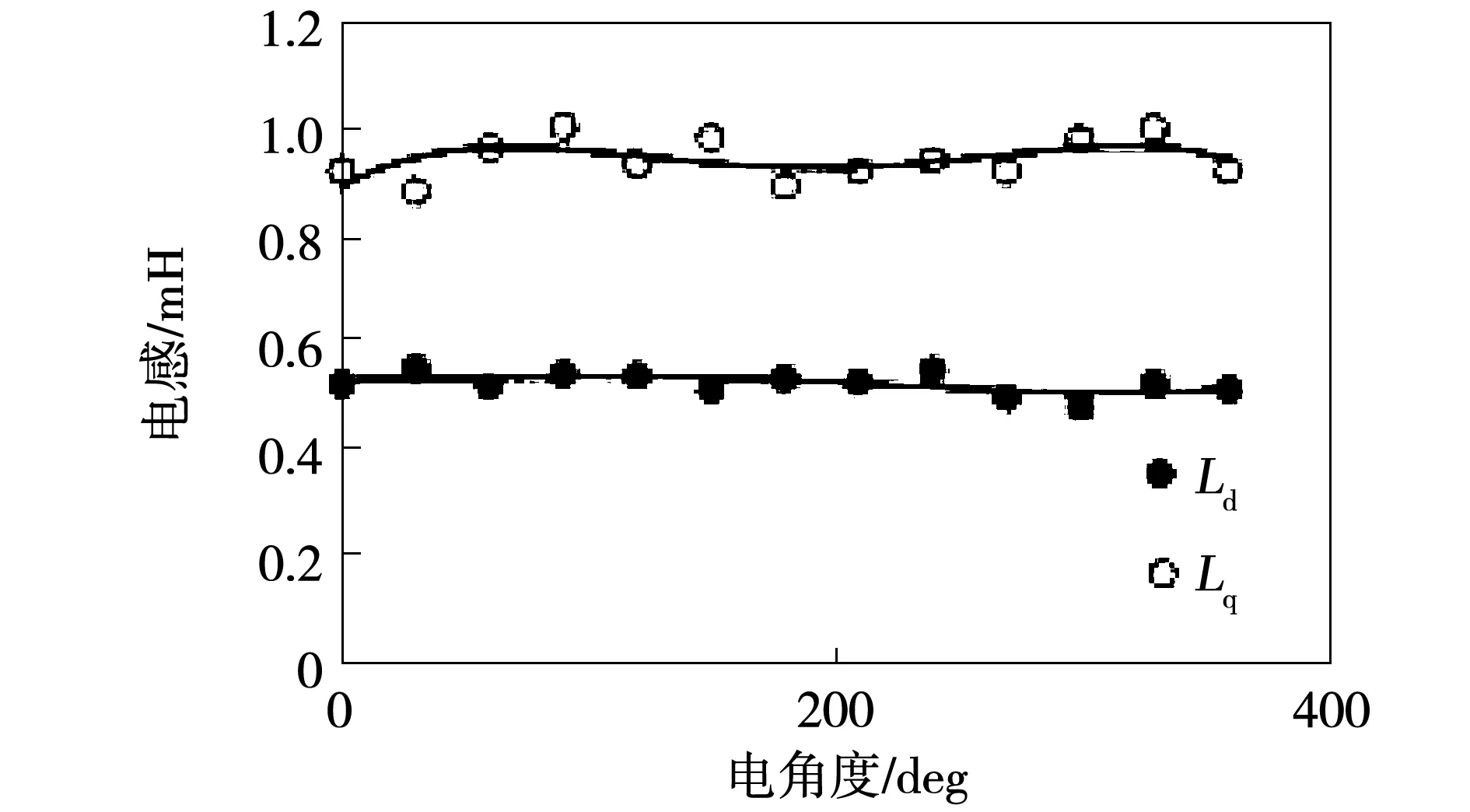
图9 原始电感曲线拟合曲线Fig.9 Curve fitting of raw inductance results

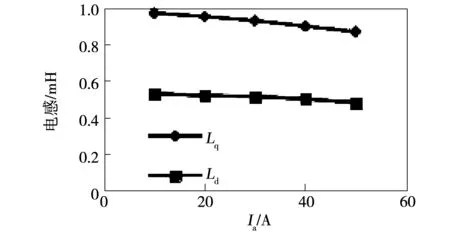
图10 电感随电流幅值变化测试值Fig.10 Test curve of inductance varying with current amplitude

如前所述，推导公式基于正弦绕组分布。但实际绕组中会有一定的空间谐波，会产生测试偏差。此外，分析过程没有考虑铁损等效电阻中的电流分量。因此采用式(4)计算，可能会产生部分奇点。在这些奇点附近测得的电感严重失真，因此在取值的时候需要把坏点去掉，然后进行拟合，这样得到的机会会更准确。

2.3 动态测试试验及试验数据处理

2.3.1 动态测试试验

动态测试永磁同步磁阻电机交、直轴电感需要专用控制器或电压型变频电源，将采用基于每安培最大扭矩控制策略的电动车用电机控制器对电机进行控制。在电机运行状态下，无法直接通过测试电机相反电势来获得内功因数角。因此，通过采用旋转变压器解码器获得电机运行过程中转子的位置。

电动车电机全工作域内需要测试点较多，而且需实时计算内功率因数角，数据采集量较大。因此本文基于Labview软件开发了数据采集和电感计算平台。通过实时采集电机端电压波形以及解码器的位置信号，以此得到所需计算角度。再通过数字电阻测量仪和功率计获得电阻值和三相电压、三相电流值以及功率因数角。测试方案如图11所示。

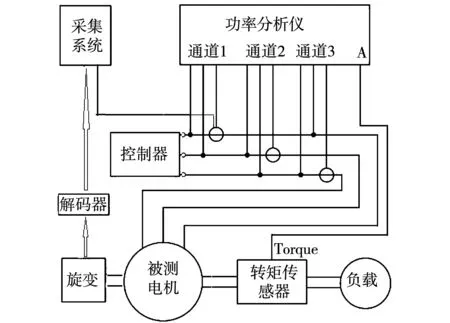
图11 动态态电感测试方案Fig.11 Dynamic measurement scheme for inductance

2.3.2 动态测试试验数据处理及计算

由于电机采用变频控制器供电，因此电压波形是PWM模式，很难通过电压波形确定相位角，因此本文通过测试电流波形和旋转变压器解码器的波形的相位差获得θi，并通过功率分析仪获得电压和电流的夹角φ，进而可以获得θu。为了提高计算精确度，电流传感器的数据波形采集过程中存在大量噪声干扰，经过后台数据FFT分析，通过数字滤波去掉高频干扰，在通过数据拟合处理后与转子位置信号比较，得到所需相位角θi。图12为电感测试系统采集的电流波形和解码器波形，其中解码器波形是通过把数字量转换成相应电压幅值获得的，以此便于实时观测。

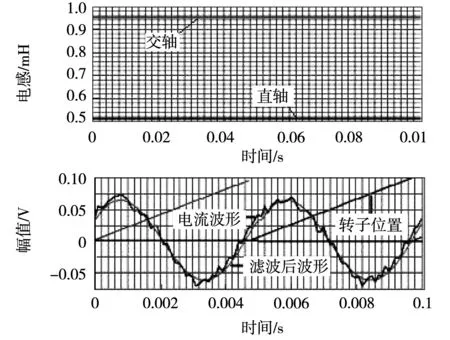
图12 电感测试系统Fig.12 Inductance measurement system

采用动态测试方法对电机进行测试，保持电机电流不变，测试交、直轴电感随转速的变化曲线。同时采用Ansoft软件根据电机动态测试过程中的参数进行交、直轴电感的仿真计算。动态测试结果和仿真计算结果对比如图13所示。采用此方法同样也可以在恒转速下，测试不同负载时的电感参数。因此采用此方法可以实现电机全工作域内的电感参数试。

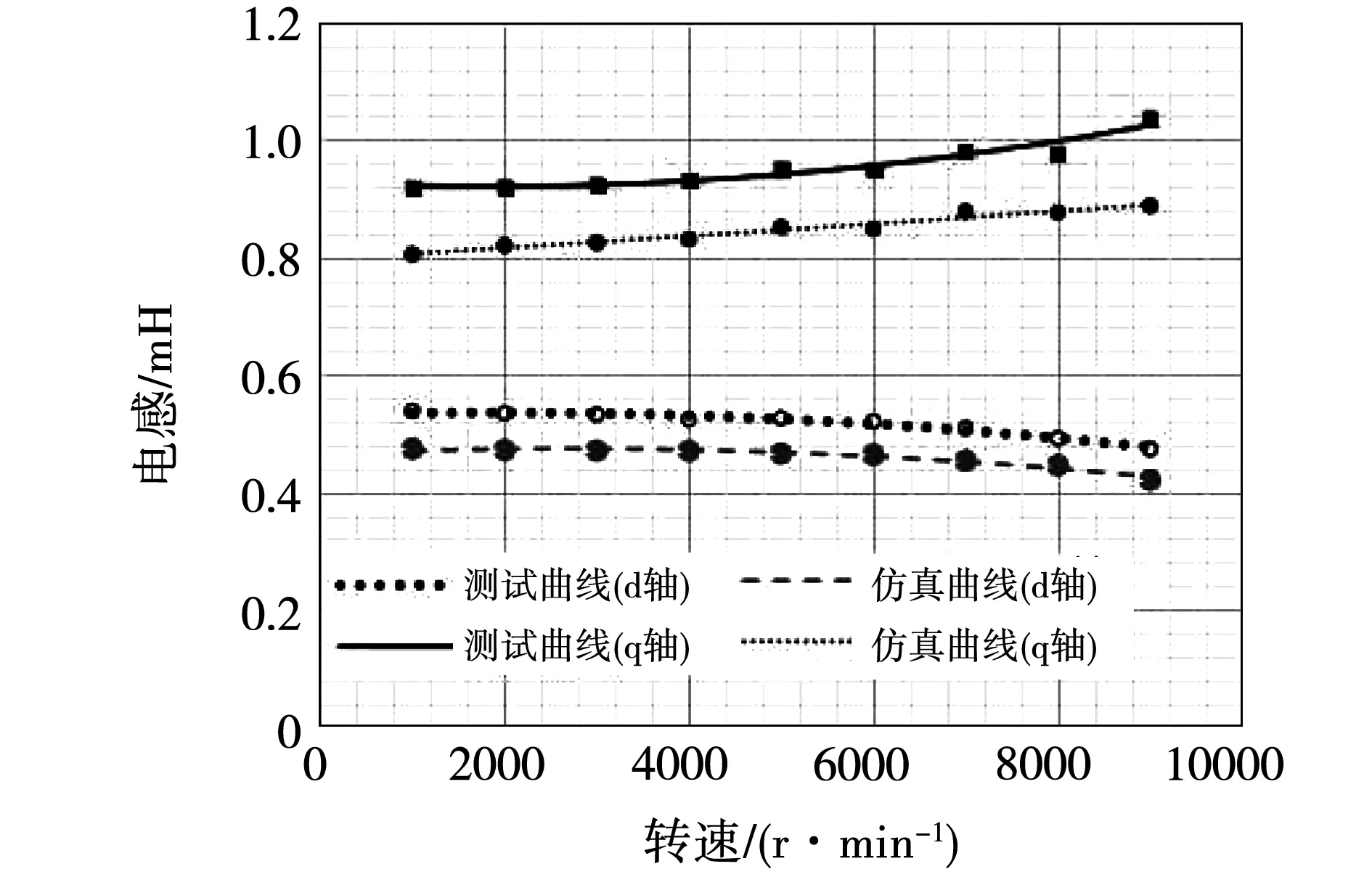
图13 交、直轴电感测试及仿真曲线Fig.13 Q-axis and d-axis inductance test and simulation curve

2.4 不同测试方法测试结果应用对比

实验室测量电感通常采用伏安法、直流衰减法、电压积分法等。但这些测量方法往往无法在额定负载工况下对电机的电感参数进行精确测试。为了验证不同电抗参数对控制的影响，又采用伏安法对同台电机进行测试，使用高频电源，通过给定电机300 Hz额定频率和10 A电流(高频电源最大输出电流)，测试电机交、直轴电感。测试结果如图14所示。

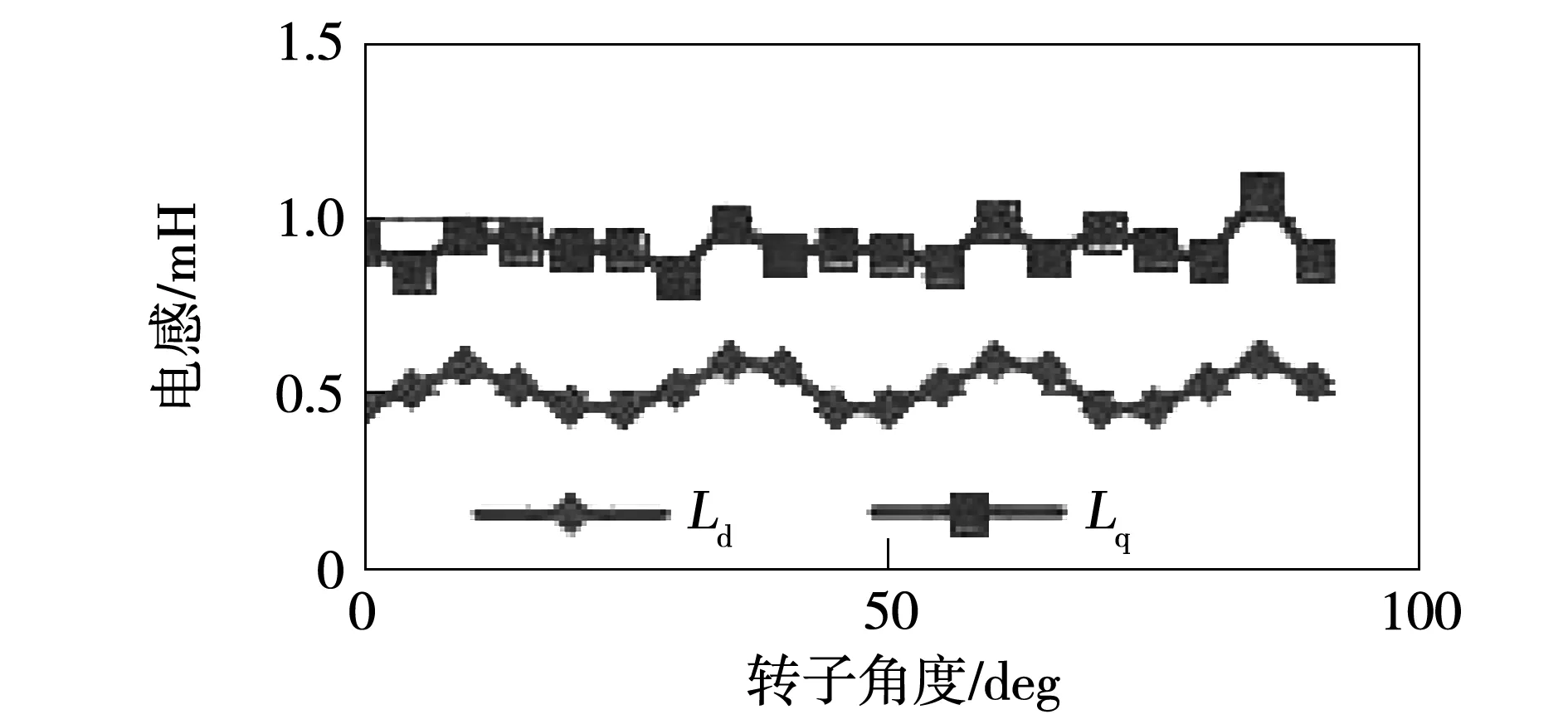
图14 交、直轴电感测试曲线Fig.14 Q-axis and d-axis inductance test curves

将不同测试方法获得的电感参数，用于一台电机控制器的数学模型中，对20 kW电机进行试验，如图15所示。在转速不变，为4 500 r/min时改变负载测试电流；在转矩不变，以29 N·m转矩为例，改变电机转速测试电流。不同方法测试的电流情况见图16和图17。

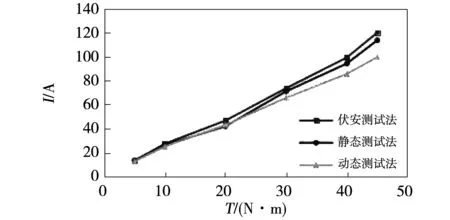
图16 电流随转矩变化曲线Fig.16 Current and torque curve

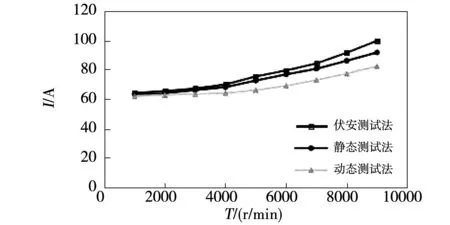
图17 电流随转速变化曲线Fig.17 Current and speed curve

通过对比可见，电机运行在相同工况下，电机控制器采用动态测试方法获得的电感参数时，变频器输出电流最小，因此动态测试方法测试得到的电感参数相对其他方法更准确。

3 结 论

本文重点研究了适用于电动汽车用永磁同步磁阻电机交轴和直轴电感测试方法，通过对一台20kW电机实验，可以得到如下结论：

1)通过试验对比，本文提出的动态测试方法得到的电感值更接近实际值，控制效果更好。动态测试法能够为电机的非线性模型提供数据支撑，根据电机不同工作区域，实现参数分段拟合，获得准确的电感参数，可以节省大量的标定工作。同时在应用测试结果的时候，为了更好的达到控制效果，调试控制器的时候需要考虑变频器输出电压存在滞后的问题，特别是在高速阶段，必要时需要采取适当补偿方法。

2)本文提出的静态测试法，若要考虑磁路饱和的影响，交流电源中的电流或电压限制是这种方法的另一个缺点，这意味着小功率电机是首选。而且相位不均会影响电感的测量，采用精确度更好些的电压源可以提高测试精确度。

3)电机在工作运行区域内，直轴电感受电流幅值和矢量位置影响较小，交轴电感受磁路饱和和交叉磁化影响较大，在电流增大时电感值明显减小，在弱磁区电感值明显增大。