基于信号局部均值分解的机械故障诊断研究

刘 力

(延安职业技术学院机电工程系,陕西 延安 716000)

旋转类设备结构较为复杂，在企业设备总量中占有较大的比例，因此做好旋转机械设备的在线监测和故障预防[1-2]，对于保证企业设备安全运行意义重大。旋转类设备正常运行与带故障运行的振动频率存在差异，结合设备振动信号的时频特征和原始故障机理，能够确定出故障的位置、类别及严重程度[3]。在线故障监测的难度在于短时间内要处理海量的样本数据[4]，对于算法的降噪能力、信号分解能力有更高的要求。基于传感器故障数据集的特征提取，在故障鉴别的准确率上要明显优于传统人工检修模式[5]，同时还能降低故障检修的人工成本，减少设备停机的时间。随着机械设备复杂程度的提高和实际作业时间的延长，故障数据集的规模越来越大[6]，给在线故障数据采集和分析带来更多的困难。现有的故障在线诊断模式包括基于模式识别的故障诊断方案[7]和基于信号分解与时频转换的故障诊断方案[8]。文献[9]提出了基于ANN(人工智能神经网络)的故障诊断方法，该方法模拟人脑神经网络的工作模式,模糊处理和训练故障大数据集合。文献[10]提出了基于LS-SVM(最小二乘支持向量机)的故障分类诊断方法，利用机器学习在故障数据处理效率方面的优势实现故障的在线诊断。上述方法都采用了窗函数截取模式[11]，在多分量信号分析时时频谱会出现交叉，影响了故障识别精度与故障诊断的效果。而HHT变换(希尔伯特-黄变换)在信号分析中结合了时频域转换的优点[12]，提高了故障信号的处理效率，但该种方法依然延续了经典小波变换的窗口平移方案，信号分解中缺乏良好的自适应性，从而导致诊断结果的均方误差值过高。

本文提出了一种基于信号局部均值分解(LMD)的故障诊断算法，通过特征向量的构建与信号特征的提取，识别出故障点的位置和故障类别。

1 机械故障信号局部均值分解

原始机械故障信号中包含系统噪声和环境噪声，导致故障信号在频率和幅值方面表现较为复杂，信号分解后IMF分量的数量持续增加，造成模态混叠现象的产生。局部均值分解的目的是提取并区分原始含噪故障信号中的调频信号和包络信号，调频信号对应PF分量的频率特性，包络信号对应PF分量的幅值特征。设降噪后的旋转机械原始故障信号函数为s(t)，t为时间。在信号区间内位于相位k的局部极值点为τk，计算τk与其邻域相位极值点τk+1的均值μk：

μk=(τk+τk+1)/2

(1)

依据极值点τk计算信号函数s(t)的包络估计值ζk：

ζk=|(τk-τk+1)/2|

(2)

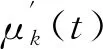
(3)

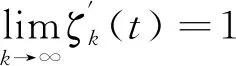
(4)

对PF分量求导，得到最终的分解信号S(t)：

(5)

式中：m为相位数量；fk(t)为PF分量的导数。

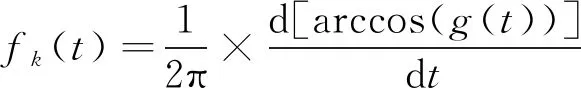
(6)

取一段相位区间，保证该段信号变化的趋势与首末两点相似，即在该段相位区间内信号的变化具有单调性。拓展分解信号S(t)的首尾两端，pk和qk分别表示分解信号S(t)的极大值和极小值，拓展信号波形匹配时的极大值和极小值对应时间节点分别为tpk和tqk，在单调的区间内寻找最优的波形匹配点，其中区间内任一点对应的时间节点为ts(t)：

(7)

式中：tp1和tq1为第一个故障信号的极大值和极小值。波形匹配中的误差值ε(t)为：

ε(t)=|tpk-tp1|+|tqk-tq1|+|S(k)-S(1)|

(8)

式中：S(1)为第一个故障信号的分解值。

当信号波形匹配的误差最小时，计算两端极大值和极小值的平均值，再将拓展后的信号分解到PF分量中，即可以有效缓解信号处理时的端点效应。在拓展信号分段中首先提取零点信号所包含的特征，然后将信号S(t)分解为N段，N为信号采样时长T与信号调制频率f乘积的两倍，即N=2Tf，基于零点数相等的基本原则，被分成的N段信号每段可以表示为ci(t)，对分解后的每段信号进行傅里叶变换并对比分段信号的频谱，分别向左、向右拓展频谱信号，分解延拓信号并截取信号的延伸部分，获得最终的分解结果。

2 旋转机械故障特征提取

将传感系统采集到的原始故障数据分为训练样本和测试样本两类，利用局部均值分解算法分别处理两类样本得到若干组PF分量。计算混合原始信号与PF分量的相关程度，并利用Fast ICA(快速独立分析因子)辅助联合降噪。重构原始虚拟故障观测信号的流程如图1所示。

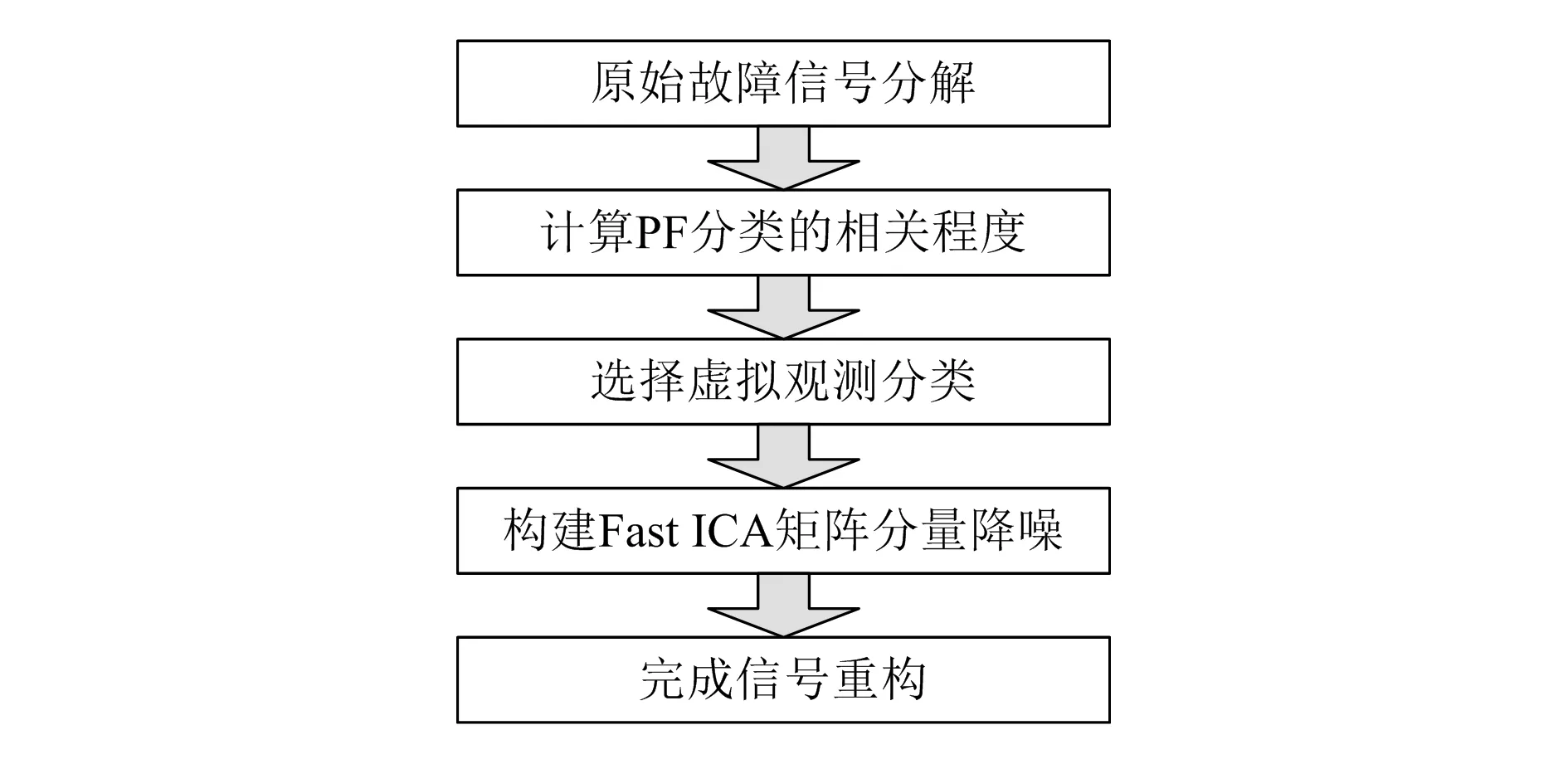
图1 机械故障数据联合降噪和信号重构流程

形成混合虚拟的二维矩阵模型后输入模型分解信号以达到滤除信号汇总噪声干扰的目的。假定信号S(t)被分解为3个PF分量，分别表示为f1=PF1(t)、f2=PF2(t)和f3=PF3(t)，其中f1位于信号波形的峰值fmax处，即f1=fmax，f2和f3分别位于峰值相位的1/2处和1/3处，利用局部均值分解算法分段提取原始振动信号的特征，振动信号的特征分量主要集中在区间[1/3fmax,fmax]。引入能量系数ei和偏度系数ζi，构建特征向量：

(9)

式中：μ和σ为各信号的均值和标准差。利用提取的故障特征构建的特征向量H表示为:

H=[e1,e2,…,eN,ζ1,ζ2,…,ζN]

(10)

3 机械故障信号诊断的实现

为减少计算量，正常状态下只使用能量参数构建特征向量，利用能量系数模拟变量进行训练和测试，得到多种故障类型下变量预测模型。由于不同类型故障的变量信号频率和幅值变化存在明显的差异，因此预测误差值大小不同，而正常状态下预测值的误差要更小。旋转机械故障信号接近于正态分布，但局部均值分解后原始故障信号分量的峭度Q和歪度W对信号的冲击敏感度增加，峭度和歪度的计算公式如下：

(11)

式中：e表示能量系数函数；i代表第i段信号。结合峭度Q和歪度W，一方面可以更好地滤除环境噪声和系统噪声，另一方面能协助信号均值分解构建特征向量。在3个PF信号特征分量中，原始故障信号包络谱峰值受到噪声的影响较少，可用相关系数增强包络谱的可靠性，相邻信号的自相关函数ρ(t)可以表示为：

ρ(t)=e[S(t)·S*(t+t′)]

(12)

式中：S*为S(t)的共轭；t′为两个相邻信号之间的时间间隔。包络谱增强后，故障信号的谱线更为清晰，特征频率的峰值和最大、最小幅值与正常信号的差距更加明显，能够准确地鉴别出设备故障的位置。信号滤波后的3个PF信号特征分量，其中2个为有效分量，1个为残余分量，计算出有效分量的峭度值和歪度值并作为信号重构的基础，残余分量被包络增强后更容易找到信号跳频和转频的最佳时点。对局部均值分解后的信号特征做归一化处理，取峭度值较大的前两组信号PF分量重构信号，在实际特征值归一化处理中平均能量的计算过程保持在原有故障频率的两倍频和三倍频，并在该特征值点上分别进行测试和训练。故障信号的分段数以分类核函数的具体点数设置为准，增强了非二次谐波干扰的处理能力，同时也可以提升对原始故障信号的处理效果。

4 实验结果与分析

4.1 实验准备

大型旋转机械设备的变速箱齿轮组是该设备的核心部件，齿轮组易出现个别轮齿脱落、严重磨损及齿轮间隙过大等故障。本文以变速恒频发电机组的变速箱齿轮组为研究对象，对其进行故障仿真。仿真实验中信号的采集周期为0.2 s，采样频率设定为50 kHz，实验系统的电机功率为350 kW，转动频率为50 Hz，齿轮组输入端和输出端的转频分别为25.5 Hz和28.5 Hz。利用搭建的实验台采集故障齿轮组的故障信号数据，为减少端点效应带来的不利影响，对信号波形做拓展和降噪处理，得到滤波处理后的故障信号数据集。对故障信号数据集做局部均值分解，并适时截断信号避免出现端点效应，得到拆分后的PF分量，提取敏感分量的细节特征，并消除虚假分量的干扰，提取信号的包络谱特征，并进行傅里叶变换。基于重构后滤波信号的基本特征，仿真实验的流程如图2所示。

图2 仿真实验流程

4.2 实验结果与分析

为验证局部均值分解算法的有效性，基于特征识别和模式识别两种不同的仿真环境，并引入ANN故障诊断方法、LS-SVM分类诊断方法及HHT故障诊断方法参与对比。对同一齿轮组的复合故障特征进行识别，旋转齿轮组的故障集合包括缺齿、过度磨损和间隙量过大，选择的训练样本数量为300，测试样本的数量为500，测试结果见表1。

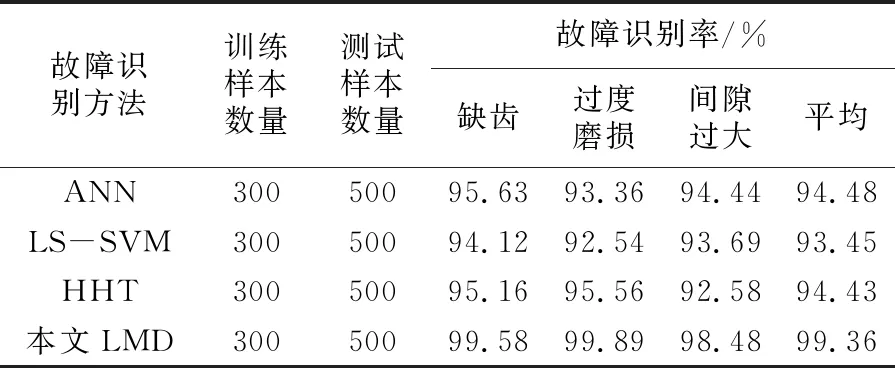
表1 复合故障条件下的特征识别对比结果

由表1可知，复合故障情况下，ANN故障诊断方法、LS-SVM分类诊断方法及HHT故障诊断方法的故障识别率分别为94.48%、93.45%和94.43%，本文设计的基于局部均值分解的故障诊断方法的识别率达到了99.36%。在模式识别环境下随机加入3种类别的故障，要求算法首先依据传感器信号判断故障的类别，然后再识别故障的严重程度。训练样本和测试样本数量分别为100和150，故障诊断结果如图3和图4所示。

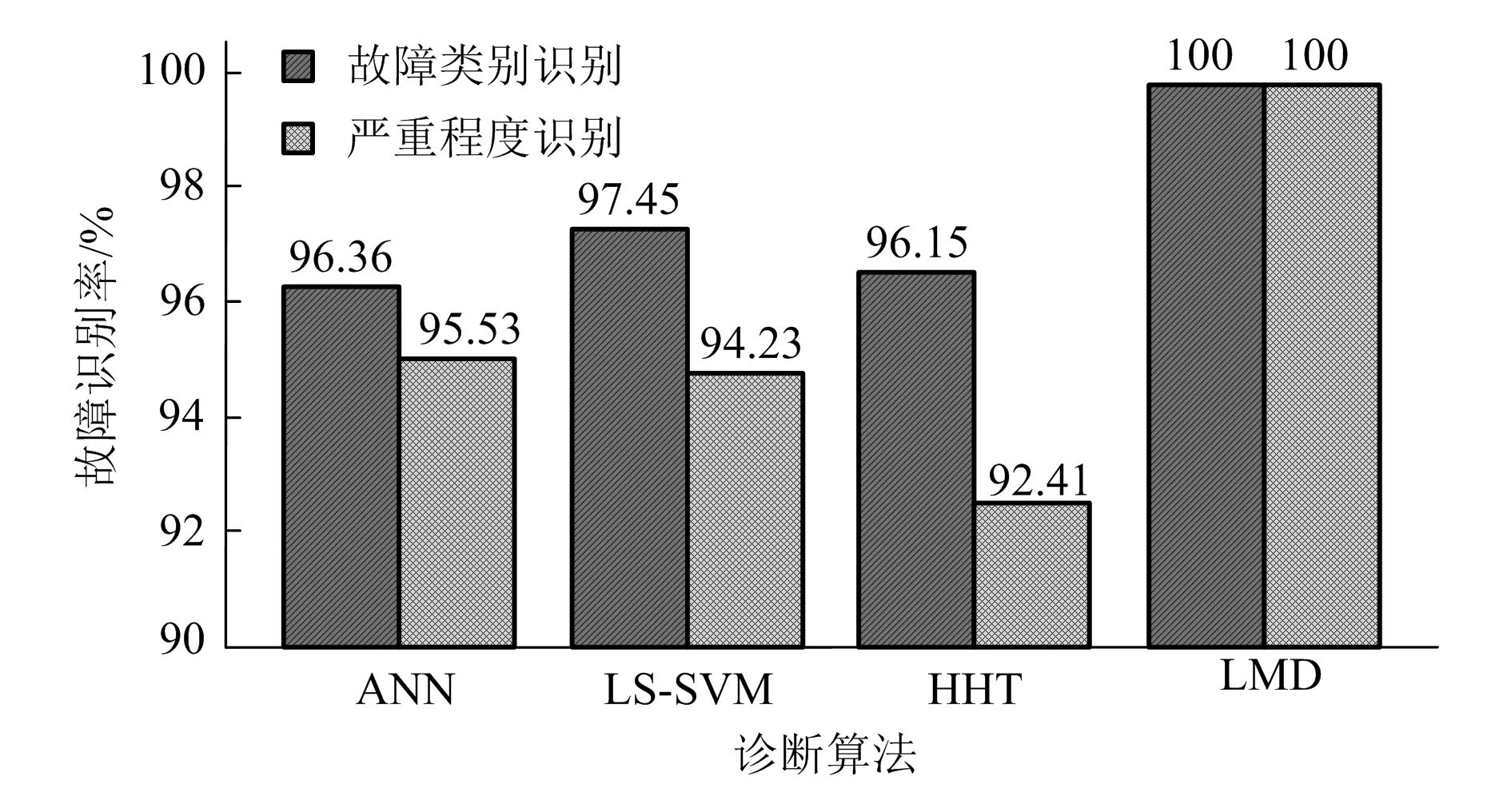
图3 训练样本各算法的故障识别情况

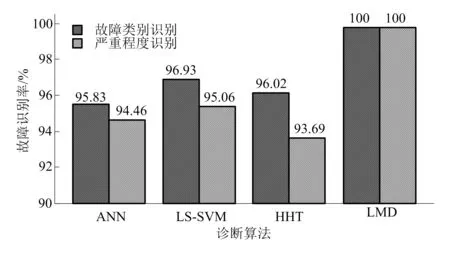
图4 测试样本各算法的故障识别情况

由图可知，在样本总量偏少的情况下，本文方法对故障类别的诊断和故障严重程度的判断率都可达到100%，表明在处理单一故障时本文算法的优势更明显。对测试信号样本做局部均值分解，采集每种故障信号，随机选取50组数据作为训练样本，结果显示，原始故障信号的特征信息主要集中于PF1分量和PF2分量中。各种故障的近似特征分量值分布情况见表2。

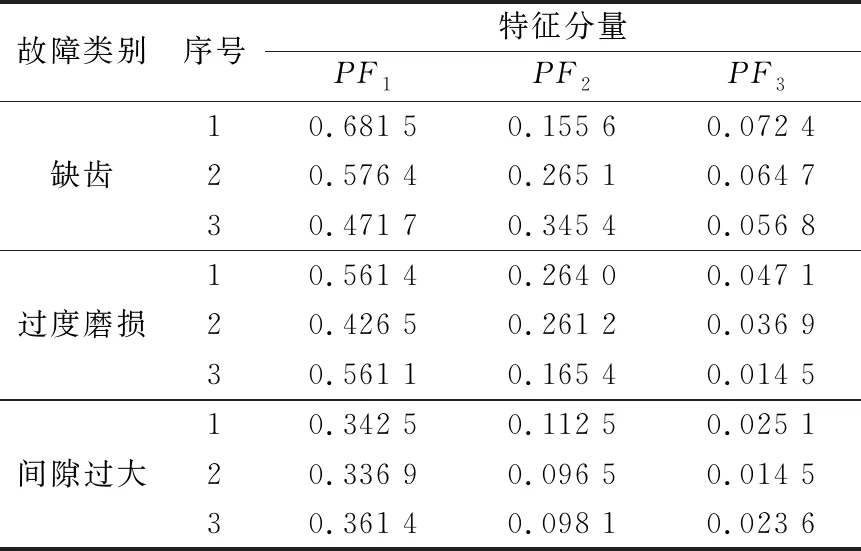
表2 近似特征分量的分布

由表2可知，不同类别故障的近似特征分量值分布与故障信号识别结果(图3、图4)变化趋势基本一致。均方差指标主要用于衡量故障诊断算法的基础性能，基于复合故障样本分析本文故障诊断方法与3种传统故障诊断方法的均方差，迭代步数设为140步，所得均方差曲线如图5所示。

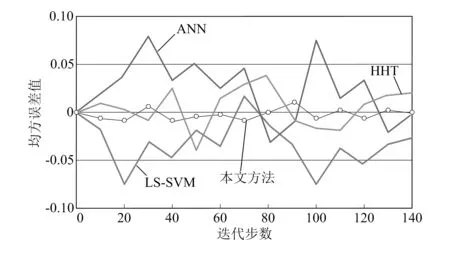
图5 不同诊断方法的均方差变化情况

从图5可以看出，本文方法的均方差变化最小，且接近于0；ANN方法以及LS-SVM方法在迭代周期内的均方差最大值均大于0.05、最小值均小于-0.05，稳定性较差。HHT方法的表现略好于上述两种传统方法，但均方差的波动与本文方法相比仍较大。经过均值分解后的原始故障大数据信号，特征信息被分散到了不同的PF分量当中，使迭代过程中信号均方误差值的变化更为平稳。

5 结束语

随着机械结构复杂程度的不断提高，故障样本集合越来越大，给故障信号特征提取带来更大的难度。针对现有ANN、LS-SVM及HHT故障诊断方法存在的不足，本文通过对原始故障信号的局部均值分解，分离噪声信号并寻找最优的波形匹配点，更准确地提取原始故障信号中的特征点。实验证明，本文提出的方法在复合故障情况下具有更高的故障识别率，故障诊断的均方差值更低。