基于Leader-Follower策略的双联AGV协同运载控制方法

楼航飞，楼佩煌，武 星，潘天宇，钱晓明

(南京航空航天大学机电学院，江苏 南京 210016)

随着自动导引运输车(automated guided vehicle，AGV)的应用场景不断拓展，受限于尺寸、结构、承载方式等因素，单AGV已难以满足大长重型部件及一些特殊部件的自动化输送需求。以飞机大型结构件输送为例，传统的车间级运输仍采用人力车或牵引车[1]。而另一方面，协同运作的多智能体系统一直以来都具备着单智能体无法比拟的优势，在感知、监控、运作等诸多方面，多智能体的协作运行表现出了更优越的信息多样性和运作灵活性[2-4]。因此，通过引入多智能体系统协作策略中队形保持的方法，构建多AGV的协同运作系统，可以解决单AGV运载能力的受限问题，极大地提高AGV的配置优化，从而进一步扩大AGV的应用场景。

目前主要的队形保持策略有基于行为法、虚结构法、领航-跟随法(Leader-Follower)、虚函数法以及图论法[5]。Leader-Follower策略因可靠性高、扩展性好，成为被广泛采用的一种多机器人队形保持方法[6]。因此，通过Leader-Follower策略实现多AGV协同运载以提高AGV的运载能力，是一种极具可行性的方案。结合现代控制方法及感知方式，诸多国内外研究者进行了基于Leader-Follower策略下的多智能体系统控制方法的研究[7-9]，以及Leader-Follower策略下大物件运载应用实现的研究[10-11]。

借鉴文献[10]用于重载AGV双模块协同的Leader-Follower策略，本文结合AGV路径跟踪的约束功能和运行稳定性，面向Leader-Follower双联队形误差自补偿方案，提出了一种双联AGV协同运载的控制模型。

1 AGV基于路径跟踪的运动学模型

为保证系统运动的灵活性，本文采用了基于Macanum轮的全向移动AGV作为运动控制单元。取AGV的控制周期为T，则基于位姿状态的全向移动AGV路径跟踪系统具有如下运动学偏差状态方程[12]：

(1)

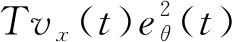
(2)

2 Leader-Follower策略下的双联AGV协同控制模型

Leader-Follower策略的双联AGV协同运载的结构简图如图1所示。支架8处安装有转动副与移动副复合的组合运动副，支架6处安装有转动副。系统内部的偏差一方面来自于视觉导引下路径7与AGV之间的距离偏差ex和角度偏差eθ，另一方面，则来自于协同系统的Follower柔性支架8处安装的位移传感器测得的队形距离偏差ΔL。

1—Follower；2,5—视觉模块；3—被搬运件；4—Leader；6,8—支架；7—路径轨迹

双联AGV协同系统的运行策略为在保证AGV路径跟踪的同时，还能保证两台AGV中心距离L(t)与期望距离L的差值收敛于0。

如图2所示，以被搬运件为纵坐标正方向建立直角坐标系，将双AGV的速度沿搬运工件进行分解：

图2 AGV主从协同模型运动误差分析

T(vy1cosα1-vx1sinα1+vx2sinα2+vy2cosα2)=ΔL(t+1)-ΔL(t)

(3)

式中：α1，α2分别为Leader、Follower与被搬运件所成的队形角度偏差；ΔL(t)为队形距离偏差，亦即两台AGV中心距离L(t)与期望距离L的差值。

协同系统的运动学偏差变化模型为：

(4)

(5)

ΔL(t+1)=ΔL(t)+T(vy1cosα1-vx1sinα1+vx2sinα2+vy2cosα2)

(6)

式中：w1和w2分别为Leader和Follower的角速度；ex1(t)和ex2(t)分别为t时刻Leader和Follower的路径距离偏差；eθ1(t)和eθ2(t)分别为t时刻的Leader和Follower的路径角度偏差；vx1，vy1分别为Leader沿车体坐标系在x轴及y轴方向的速度分量；vx2，v2y分别为Follower沿车体坐标系在x轴及y轴方向的速度分量。式(4)为Leader偏差变化模型，式(5)为Follower偏差变化模型，式(6)为双AGV队形距离偏差ΔL变化模型。则协同系统偏差变化率为：

(7)

(8)

(9)

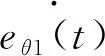
根据偏差模型及偏差变化率，设计协同系统的运动学控制模型如下：

(10)

(11)

式中：k1，k2，k3，k4，k5均为系统的控制参数。对Leader和Follower分别设置Lyapunov函数为：

(12)

(13)

式中：V(ei1)和V(ei2)分别为Leader及Follower的Lyapunov函数，ei1和ei2分别为Leader及Follower的广义偏差变量。

对Leader及Follower进行分析：

由此证明Leader与Follower的控制模型具备Lyapunov稳定，式(10)与式(11)的运动控制模型下的角度偏差eθ1，eθ2与距离偏差ex1，ex2，ΔL可最终收敛于0，双联AGV运载系统具备路径跟踪与队形保持的能力。

3 仿真与分析

本文通过MATLAB R2016a平台进行AGV的路径跟踪运动控制仿真实验。

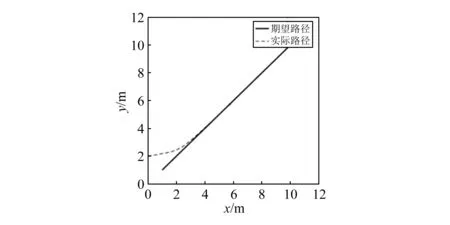
图3 直线路径跟踪图

图4 Leader直线路径偏差变化图

进一步地，对圆弧路径下的Leader路径跟踪控制模型进行仿真实验，跟踪效果如图5所示。起始点为(3,2)，起始角度为-π/4，设置纠偏系数k1=0.2，k2=0.8；期望路径起始点为(4,2)，起始角度为π/2，仿真时间为10 s，仿真控制周期为0.05 s，期望角速度为π/10 rad/s，期望线速度为2π/5 m/s，期望路径的圆弧方程式为(x-2)2+(y-2)2=4。图6为Leader进行圆弧路径跟踪时的偏差变化图。在3.0 s时，角度偏差收敛于0；在6.5 s时，距离偏差收敛于0。

图5 圆弧路径跟踪图

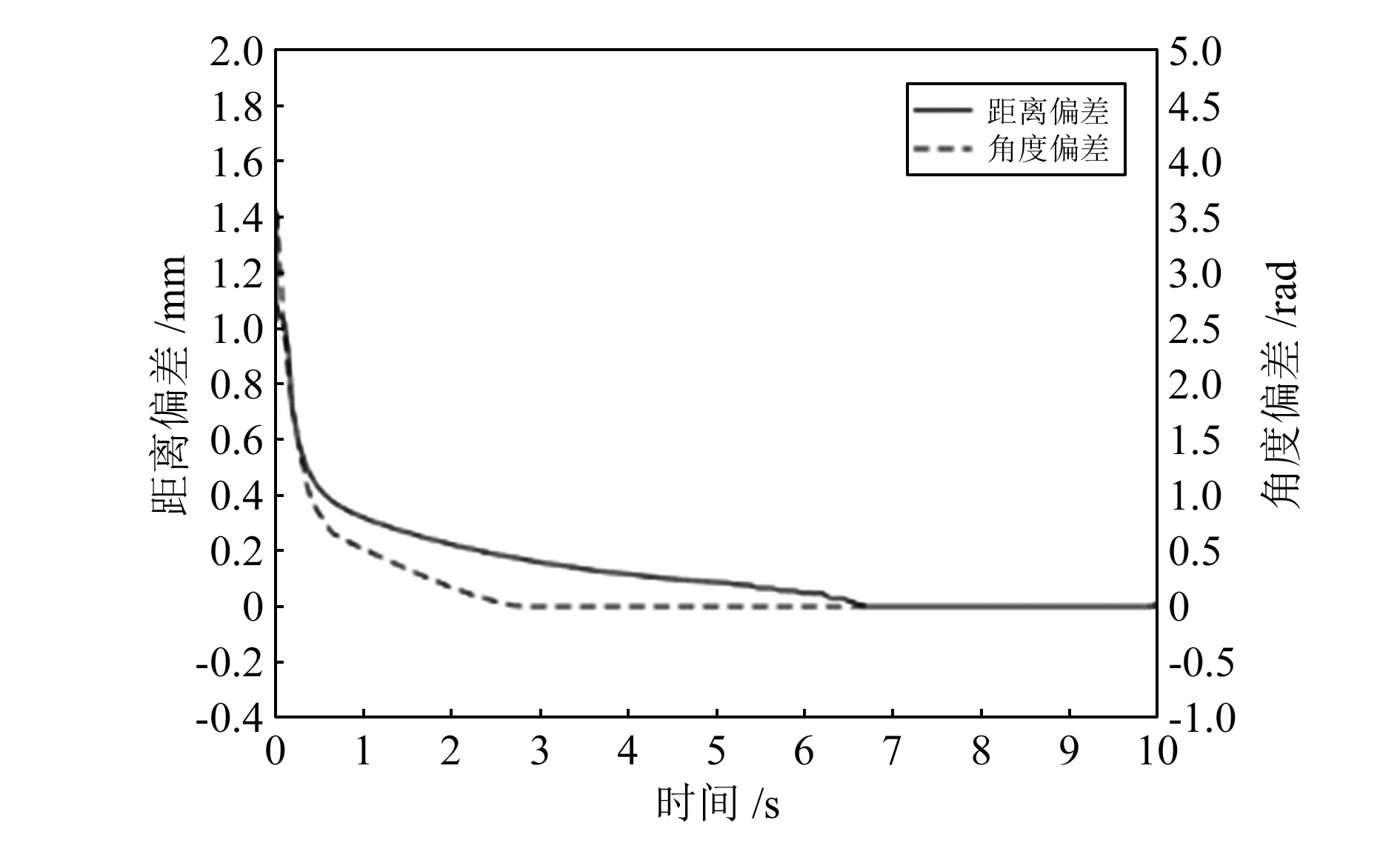
图6 Leader圆弧路径偏差变化图

因此，综合图3到图6可得，在进行直线或圆弧路径跟踪时，Leader的运动学控制模型都具有良好的偏差收敛效果。

进一步分析双联AGV系统内Follower的控制效果，依据上述引入队形距离偏差ΔL得出的Follower控制模型，进行单一时刻偏差收敛仿真分析。初始时刻路径距离偏差ex2=20 mm，路径角度偏差eθ2=π/3，双AGV队形距离偏差ΔL=-30 mm(本文为统一曲线图y轴的刻度，将ΔL和Δx的单位转化为dm)，设置k3=1.0，k4=0.5，k5=1.5，仿真结果如图7所示。

图7 Follower偏差变化图

在图7中，路径距离偏差Δx及路径角度偏差Δθ在2.0 s时收敛于0，队形距离偏差 在2.7 s时收敛于0。因此，通过仿真实验可以得知Follower运动学控制模型具有良好的偏差收敛效果。

4 实验研究

为了验证前述双联AGV协同运载运动学模型的有效性，进行两台全向AGV协同搬运一件长尺寸物件的实验。双AGV呈前后放置，运行过程中，沿着同一色带标识的路径前进，其中双联AGV运行路线如图8所示，实物系统如图9所示。

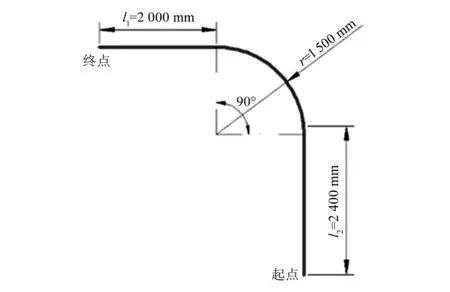
图8 双联AGV协同路径跟踪路线图

图9 双联AGV协同搬运实物图

设置的初始状态如下：Leader距离偏差ex1(0)=20 mm，角度偏差eθ1(0)=30°；Follower距离偏差ex2(0)=-20 mm，角度偏差eθ2(0)=30°；初始运行速度v为0.4 m/s，初始队形偏差ΔL(0)为60 mm；实验轨道圆弧段半径r为1.5 m，圆弧圆心角为90°。在0 s时同时启动Leader和Follower，开始运行AGV系统。实验时，通过视觉模块得到Leader及Follower实时的角度偏差eθ1,eθ2和距离偏差ex1，ex2，通过安装于支架处的角度传感器得到AGV相对于被搬工件的角度值a1和a2，通过位移传感器获得队形距离偏差ΔL。控制方案为在Leader及Follower运动学模型基础上，利用单片机结合实时操作系统，固定控制周期下滚动刷新离散化的速度及角速度控制量，实现Leader和Follower双AGV组合的路径跟踪与协调同步运行。图10为Leader的距离偏差ex1及角度偏差eθ1变化图。在2.0 s时Leader的距离偏差ex1值下降到0 mm，并在0 mm上下波动，在1.8 s时Leader的角度偏差eθ1值下降到0。图11为Follower的距离偏差ex2及角度偏差eθ2变化图，在第10.0 s后，Follower进入圆弧路径，在16.0 s左右出圆弧段。Follower在2.1 s时距离偏差收敛于0 mm，并在0 mm上下波动，在1.9 s时角度偏差下降到0°。图12为Leader与Follower间队形距离偏差ΔL变化图，在2.0 s时ΔL收敛于0 mm。因此，综上可以得出，采用前述第2章的运动学模型可以有效地使Leader及Follower的路径距离、角度偏差及双联AGV队形距离偏差ΔL收敛，验证了运动学模型可以有效地使双联AGV系统进行路径跟踪的同时进行队形保持。

图10 Leader偏差变化图

图11 Follower偏差变化图

图12 队形距离偏差ΔL变化图

5 结束语

针对大部件自动化输送的场合，本文融合单台全向移动AGV的路径跟踪运动学模型与Leader-Follower策略下的队形保持方法，设计并实现了一种双联AGV协同运载的系统。该协同运载双联AGV系统实现了AGV的配置优化，扩大了AGV的应用场景，为多智能体协同运行系统的实现和应用提供了新的思路。