基于模块化的家庭医疗呼吸器设计研究
吴康鑫,黄 冠,李 颖
(湖北省肿瘤医院,湖北 武汉 430000)
由于呼吸系统疾病患病率呈直线上升趋势,民众对家用呼吸器的需求愈发强烈。然而呼吸器的应用风险等级较高,若操作不规范或者机器工作异常,均有可能威胁到使用者的生命安全[1]。家用呼吸器在使用中主要有潜在风险以及显/隐性风险。潜在风险是指尽管呼吸器的显示值与设置值一致,然而却与真实值相差较大的情况,这易引发呼吸器工作异常。隐性风险是指机器显示值与设置值不一致导致机器预警失灵的情形。显性风险是指因呼吸器应用不规范造成呼吸器部分功能缺失的情形。模块化设计是一种新型产品设计思想,主要依据产品功能,分模块对产品进行设计[2]。因为流速控制模块对于上述风险管控意义重大,为了提升呼吸器的安全性,本文以模块化设计思想为载体,对呼吸器的流速控制模块展开详细设计。
1 基于模块化的家用呼吸器流速控制模块设计
1.1 内模PID控制的模块化实现流程
作为一种新型产品设计方法,模块化以其标准化、批量化以及定制化等优点而备受广大设计者青睐。模块化本质上进行的是产品功能分解与组合操作,关键之处在于依据需求进行精细的模块划分,并依据模块优势对模块进行组合,以最大化满足消费者需求为目标,是一种有效的产品设计方法。本文在充分探析家用呼吸器市场需求与产品功能定位的基础上,依据模块化思想对家用呼吸器进行功能划分。家用呼吸器分为基本功能与辅助功能两大板块,其中基本功能包括控制模块、存储模块、监测模块以及电源模块,辅助功能涵盖人机界面模块、加热与湿化模块,这些功能模块进行组合就会形成模块化产品。鉴于篇幅限制以及流速控制模块在呼吸器安全性保障方面的重要作用,本文以模块分解得到的流速控制模块作为研究主体,对其进行详细设计,流速控制模块与呼吸器其余模块之间按照产品特征参数形成的映射关系进行接口设计与模块配置。流速控制模块运用的控制方法为比例、积分、微分控制(PID控制),PID控制具有适用性强、鲁棒性高等优点,是一种应用广泛的控制方法[3]。然而PID控制也存在参数调整困难以及非线性扰动等问题,因此需要对其进行优化[4]。将内模控制与PID控制进行结合,能有效解决此类问题。内模PID控制只要一个调整参数,该参数不仅能够有效控制系统的动态响应,还能降低系统干扰性,具有较强的响应度与鲁棒性,内模PID控制器的结构如图1所示。
图1中,Q(s)表示内模控制器,M(s)表示控制过程的数学模型,P(s)表示整个控制过程,D(s)表示控制流中的扰动信息传递函数,r,y,d分别表示控制器的输入、输出以及干扰信号,s表示控制器;z表示反馈信号;u表示干扰次数。将内模控制器Q(s)与控制过程的数学模型M(s)进行联合,就可以得到该模型的反馈控制器,用C(s)表示:

图1 内模PID控制器典型结构
(1)
故在不考虑干扰性的情况下,输入信号、输出信号间的关系为:
(2)
式(2)表示内模控制器的开环响应,此处考虑干扰信号d对输出信号造成的影响,则有
(3)
将式(2)与式(3)合并,可得:
(4)
式(4)表示该控制器的闭环响应。
故由此可得到内模PID控制系统的反馈信号z(s);
z(s)=[P(s)-M(s)]u(s)+D(s)d(s)
(5)
由式(5)可知,只有在Q(s),M(s)相匹配的情况下,才可对跟踪设定值进行有效控制。一般的闭环控制过程中,控制过程的输出信息为反馈信息,这种情况下的干扰信息易与其他因子混合在一起,对控制效果造成较大影响。若控制过程中各模型间的匹配度较高,那么扰动因子即为反馈信息,此时可以有效控制模型,且处于理想状态下,d(s)=0,那么无反馈信息出现[5]。然而由于实际工作环境的差异性,控制过程中各模型匹配性通常不高[6]。另外假定控制过程中的数学模型位于右平面零点处,且有Q(s)=M-1(s),此时Q(s)极点位于右半平面,这种状态下的控制器具有不稳定性。再者如果Q(s)有超前项,M(s)有滞后项,那么C(s)就会逐渐接近无穷大,控制系统就会出现大幅度的振荡。为了解决这个问题,需要对内模PID控制器进行分步设计。首先构建一个分解系统模型,即将M(s)进行分解,分解为M+(s)和M-(s)两个部分,且满足公式(6):
M(s)=M+(s)M-(s)
(6)
M(s)中的时滞以及半平面零点均用M+(s)表示,而其最小相位则用M-(s)表示。接下来需要将滤波器导入内模PID控制器中,也就是将低通滤波器加至最小相位处,以提升控制鲁棒性,引入模型如公式(7)所示。
(7)
式中:λ为滤波器参数,即内模PID控制模型中唯一一个需要接受整定的参数;n为滤波次数。经过滤波处理后得到了新的内模控制器Q(s),将其引入式(1)得到了反馈信息控制的数学表达C(s)。再利用数学转换,就可以将内模控制转化为PID控制,从而得到最优的滤波器参数,即实现了内模PID控制。
1.2 基于内模PID控制的呼吸器流速控制模型设计
呼吸器流速控制实质上是一个反馈信息控制过程,在反馈控制过程中,最重要的3个要素依次为测量、比较以及执行[7]。测量与变量关系密切,可通过不断与误差相比较,利用误差反复调整系统输出的方式提高控制精度。家用呼吸器通常运用传感器对流速进行测量,对应的执行机构为比例阀[8],本文研究的关键就在于通过算法控制实现理想的流速控制。家用呼吸器主要由两部分组成,分别为气路模块与电子控制模块,详细情况如图2所示。
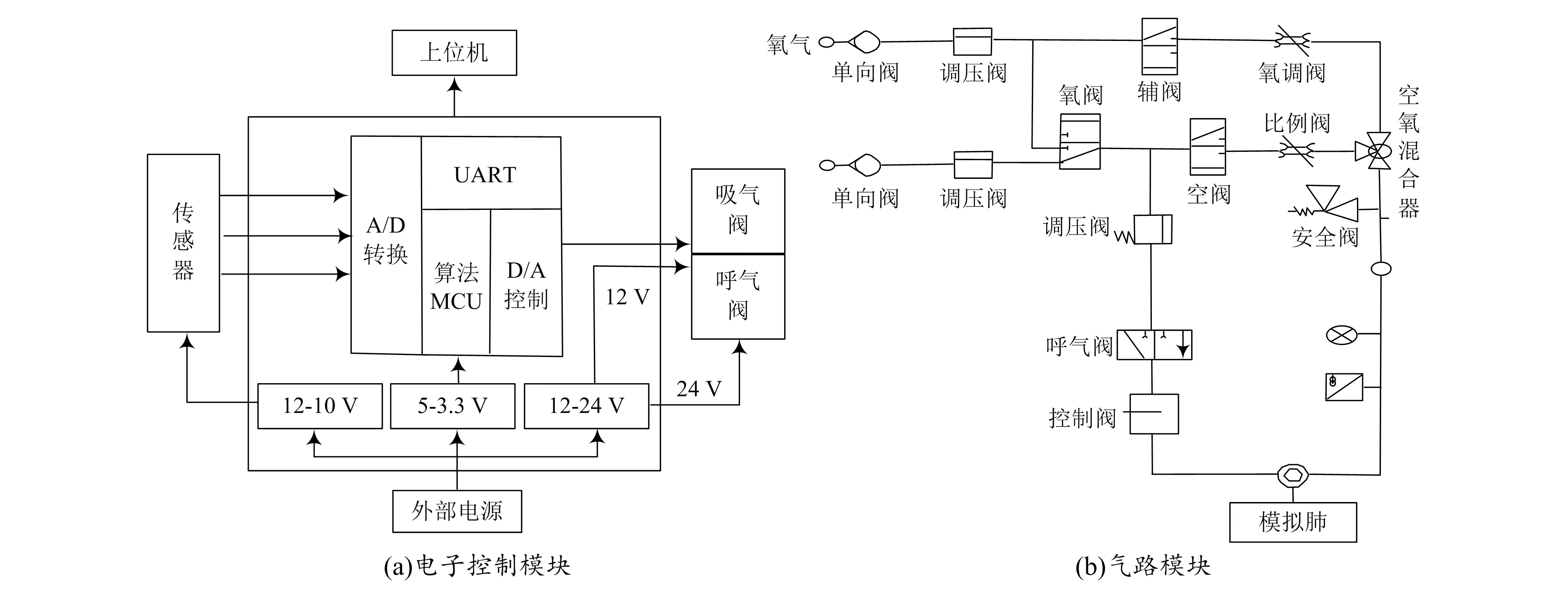
图2 家用呼吸器系统结构
气路模块是指气体运输系统,涵盖气体存储、压力支持以及气体混合等多个结构[9]。电子控制模块主要包含传感器结构、微控制器结构以及电源结构[10]。利用时域法构建流速控制的数学模型,同时利用多容惯性传递函数对过程进行控制,多容惯性传递函数的常用函数有3种,分别是一阶、二阶惯性延迟与n阶惯性延迟,通过该传递函数进行建模能够有效减少计算量,降低数据处理难度。由于在呼吸器的闭环控制中,PID算法对模型精度要求较低,且流速与传递函数阶数间具有非线性关系,故综合考虑下呼吸器流速控制器的设计主要依赖于低阶传递函数,如多容惯性传递函数的二阶惯性延迟函数,详见式(8)所示:
(8)
式中:G(s)为二阶惯性延迟函数;e-τs为延迟相;τ为纯延误时长;T1,T2分别为一阶、二阶惯性延迟的真实时间;K为增益。T1,T2,K3个参数均需要利用相关方法进行确定,常用的方法有作图法与响应曲线拟合法。作图法首先对阶跃响应进行控制,以图3(a)为例,对阶跃响应过程进行说明。在图3(a)中曲线拐点处作对应的切线,假定切线与时间轴以及渐近线间的交点依次为A,B。τ,T值均可由图3得到,K的计算公式为:
(9)
式中:y(∞)表示系统稳定响应;y(0)表示不存在激励的控制输出;Δu(t)为阶跃信号的输入性幅值。在绘制切线时,由于随意性较大,会对参数τ,T值造成较大的影响,因此作图法的准确性较低。图3(b)表示曲线拟合求残过程,曲线表示控制过程的阶跃响应曲线,在初始时刻加入阶跃信号。为了确定式(8)中的相关参数,需要移除对应的延迟部分,并归一化处理数据,同时去除量纲影响。

图3 函数的确定方式示意图
移除式(8)中的延迟部分,同时忽略增益K,传递函数G(s)可以简化成G′(s),如式(10)所示:
(10)
假定T1≥T2,则可对式(10)进行拉普拉斯反变换处理,得到式(11)所示的时域函数模型,即阶跃响应。
(11)
式中:y′(t)为阶跃响应值,其涉及两个未知参数,可以在图3(b)中随机选取两点,坐标分别为(t1,y′(t1))与(t2,y′(t2)),从而确定对应的未知参数值。通常将y′(t)取为0.4,0.8,并确定对应的时间t值,得到如下方程:
(12)
为了简化方程组的求解形式,对式(12)进行简化,可得:
(13)
利用响应曲线拟合法确定参数,K值依旧用式(9)求取。由此可知,用响应曲线拟合法求取模型参数具有更严密的逻辑推导性,可使模型参数更精确,因此利用响应曲线拟合法建立呼吸器流速控制数学模型。给定3种阶跃信号幅值,分别为600,800,1 000,据此分别建立3种内模PID控制模型,并采集对应的数据进行曲线拟合,拟合结果如图4所示。

图4 3种模型的系统阶跃响应曲线

2 家用呼吸器流速控制性能检测
为了验证本文设计的内模PID控制器的性能,设置对照实验,即3个内模PID控制器为实验组,传统比例控制器为对照组,4种控制器均在对应的呼吸器平台上进行测试,得到差异化工作环境下的性能数据,并将其绘制成曲线图。数据采集与传输通过Windows软件(上位机)完成,同时上位机利用UART端口与呼吸微控制系统(下位机)完成通信工作,完成通信需要配置相关参数,包括通气潮量、工作模式等。实验中呼吸器的工作模式为间歇正压通气(intermittent positive pressure ventilation,IPPV),对应的呼吸频率设置为15 times/min。进行性能测试时,依次修改呼吸器工作条件,并记录下4种控制器的情况,通过对比来了解各控制器的性能。为了提高实验准确性,共做了8组对照实验,每组实验的理论流速均不同,鉴于篇幅原因,这里选取理论流速的最小值(150 mL/s)与最大值(625 mL/s)进行详细分析,实际潮气量定为400 mL,呼吸比定为1∶1,其中理论流速取最小值时各参数的详细设置见表1。

表1 潮气量与流速统计(实际潮气量为400 mL,呼吸比1∶1)
表1中的波动百分比为流速振荡峰值与实际流速值的比值,超调量为实际流速最大值同其稳定值之差,超调百分比为超调量占流速稳定值比例。由表1可知,实际潮气量为400 mL时,内模PID控制器与比例控制器的流速值分别为170 mL/s与160 mL/s。为了更方便对4种控制模型的工作状态进行检查,通过相关软件绘制了对应的实时流速曲线,详细情况如图5所示。
由图5可知,3个内模PID控制器均较为稳定,即使是稳定性较差的控制器3也将振荡度控制在了13%以下,前两个控制器更不必说,波动幅度低于5%,这种小波动肉眼很难观测到。而比例控制器的振荡度已经高于65%,在用模拟肺开展实验时,能看出异常突出的波动。因此综合来看,本文设计的内模PID控制器具有较好的稳定性,符合家用呼吸器的平台使用标准。接下来将实际潮气量改为1 100 mL,且将呼吸比改为2∶3,其余条件保持不变,探究最大理论流速值条件下的实际流速情况,实验测试数据见表2。

图5 最小理论流速条件下的实时流速曲线
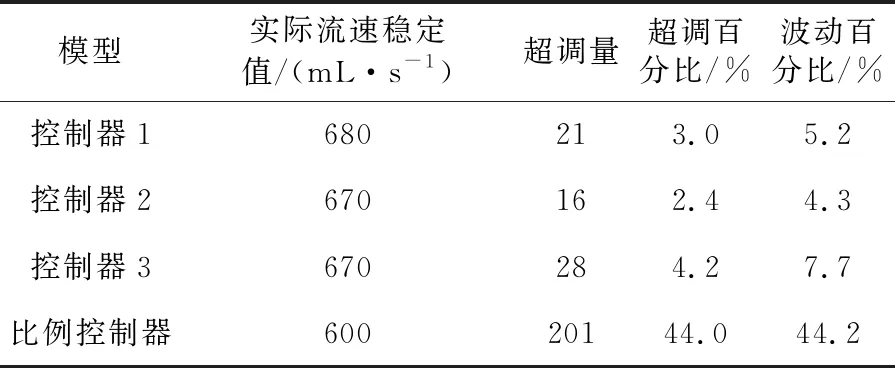
表2 潮气量与流速统计(实际潮气量为1 000 mL,呼吸比2∶3)
由表2可知,实际潮气量为1 100 mL时,内模PID控制器与比例控制器的流速稳定值分别为680 mL/s、670 mL/s与600 mL/s,且内模PID控制器的超调量最大值不超过30,而比例控制器的超调量竟然高于200,可看出内模PID控制器具有更高的流速稳定性。为了进一步分析4种控制器的流速变化情况,根据有关数据绘制了对应的实时流速曲线,详细情况如图6所示。
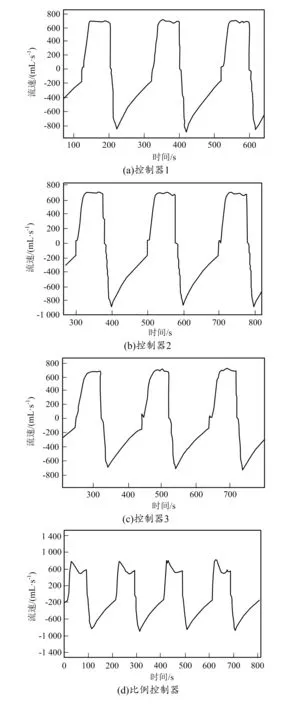
图6 最大理论流速条件下的实时流速曲线
由图6可知,内模PID控制器3的理论流速最大值均低于800 mL/s,最小值均大于-500 mL/s,而比例控制器的理论流速最大值高于800 mL/s,最小值小于-500 mL/s。另外在大流速下,内模PID控制器的振荡度皆低于5%,而传统比例控制器的振荡度却高于40%,由此可知,无论是在低流速还是高流速条件下,内模PID控制器均具有较好的稳定性,综合性能优于比例控制器。
3 结束语
基于模块化的家庭医疗呼吸器设计的关键在于按照功能划分关键模块,本文以模块化设计思想为启示,在分析家用呼吸器功能模块的基础上,选取最重要的流速控制模块进行详细设计。通过构建内模PID控制器,实现对流速的稳定控制,有效降低医疗事故风险。为了验证流速控制器的有效性,开展了相关呼吸实验。实验结果显示,在低流速与高流速两种不同条件下,内模PID控制器与比例控制器的流速值相差较小,且内模PID控制器1与控制器2的振荡度低于5%,控制器3振荡度略高,但也保持在13%以下,而比例控制器的振荡度显著高于内膜PID控制器。故同传统比例控制器相比,内模PID控制器的振荡度更小,性能更优。尽管本文的研究对于模块化家用医疗呼吸器设计具有一定的参考意义,但是实验中还存在对照组数设置较少的问题,后续有待进一步完善。

