基于2-PSR/RUPR并联机构的位置逆解及工作空间分析

李泽辉，宋胜涛，李瑞琴，胡 健

(中北大学机械工程学院，山西 太原 030051)

在包装盒加工生产线中，由于自动化效率高，加工速度快，在粘接过程中很容易出现漏胶、少胶现象，盒子粘接不紧会产生次品。若重新放回机台粘胶，则难以把握加工进度；若作为废品丢弃，则会造成浪费，不利于绿色环保。

2-PSR/RUPR并联机构是针对包装生产线上盒体漏胶的问题提出的。该并联机构是2-PSR/UPU和2-SPR/RUPR经过构型结合，得到的可以实现两转一移特性的新机构。于靖军等[1]对机构自由度的运算规则提出了系统的方法，方便进行自由度的分析计算。王新宇等[2]提出了一种2-PSR/UPU并联机构，主要针对在倾斜角度不同的斜面上旋盖的问题。罗建国等[3]针对3-RRR并联机构运动中出现的耦合问题，进行了SolidWorks和MATLAB运动学仿真分析。庞国旺等[4]提出一种3-UPS/SP4自由度并联机构，其有较大的工作空间，可应用于包装领域的点胶和喷漆。马世豪等[5]提出一种2-SPR/RUPR并联机构,得到了蘑菇云状的可达工作空间，适用于曲面上的喷绘和点胶。Xu等[6]提出了基于极限约束的一平移二转动的并联机构的类型综合分析理论。Wang等[7]在原有的喷漆设备基础上，对三自由度并联机器人做了优化改进。达悦生等[8]提出了一种与传统坐标系描述法不同的、改进的D-H模型方法,经此方法获得的结果与仿真得到的结果进行对比,证明了改进后的D-H法具有可行性。

针对包装盒生产上的漏胶问题，本文提出了一种3自由度2-PSR/RUPR并联机构，并对其进行了运动学分析。

1 并联机构构型及其自由度计算

2-PSR/RUPR并联机构由三边相等的静(下)、动(上)平台和3条支链(支链PSR-I、支链PSR-Ⅱ和支链RUPR)组成，机构模型如图1所示。

图1 2-PSR/RUPR并联机构模型

建立机构坐标系如图2所示。平台的顶点为A1、A2、A3和B1、B2、B3，上下平台均为等边三角形，且两者全等，分别取上下平台两外接圆的半径为rA,rB。对于动(上)平台，建立动坐标系{A}:OA-XAYAZA，ZA轴垂直平台向上，XA平行于A1A2，YA位于OAA3连线的延长线上；同理，对于静(下)平台，建立静坐标系{B}:OB-XBYBZB，ZB轴垂直静平台向上，XB平行于B1B2，YB位于OBB3连线的延长线上。

图2 2-PSR/RUPR并联机构坐标系及各转动副布局

采用螺旋理论分析机构自由度[9]。首先取支链PSR-I进行分析研究，建立支链坐标系B1-x1y1z1，z1轴垂直于平台向上，x1轴平行于B1B2，y1轴符合右手规则，如图2所示。图中$11表示在B1-x1y1z1坐标系下支链P副的运动螺旋，$12,$13,$14表示支链S副的运动螺旋，$15表示支链R的运动螺旋。其运动螺旋系表示为:

(1)

式中：ai,bi,ci(i=1,2,3,4,5)是与运动轴线相关的变量，其大小与问题本身无关。

(2)

此约束螺旋是一个力线矢，约束x1方向的平移,同时x1平行于XB轴。

支链PSR-Ⅱ的分布方式和支链I相同，在此不再赘述。

$31表示在B3-x3y3z3坐标系下沿y3轴方向的支链R副运动螺旋，$32,$33表示支链U副运动螺旋，$34表示P副运动螺旋，$35表示沿x3轴方向的R副运动螺旋。

则支链RUPR的运动螺旋系为：

(3)

(4)

此约束螺旋是一个力偶矢，约束z3方向的平移,同时z3平行于ZB轴。

综合分析得到2-PSR/RUPR并联机构的2个力线矢和1个力偶矢，可以实现沿ZB方向的平移以及绕XB轴和YB轴的转动，即为3个自由度。在此基础上根据修正的Kutzbach-Grübler公式对以上自由度的正确性进行验证：

(5)

式中：M为机构的自由度；d为机构阶数,d=6；n为构件总数目(包括机架),n=8；g为运动副总数目，g=9；fi为第i个运动副的自由度数；ν为并联冗余约束，机构为单环机构，没有并联冗余约束的影响，得到ν=0；ζ为局部自由度，分支螺旋系没有线性相关情况出现，得到局部自由度ζ=0。

综上所述，两种计算方法得到的并联机构自由度均为3。

2 并联机构的位置分析

2.1 PSR支链的运动逆解

运动逆解：已知动平台在静坐标系OB-XBYBZB中的位置BOA=(x,y,z)T和姿态角(α,β,γ)，求各个杆的长度di，i=1,2,3。平台位姿可以用Z-Y-X型的欧拉角表示，即动平台先绕动坐标系OA-XAYAZA的ZB轴转动α角，之后在新的坐标系下绕YB轴旋转β角，最后绕XB轴旋转γ角。由式(2)和(4)可知，并联机构可以沿着ZB方向平移，绕XB轴和YB轴转动,得到最终旋转矩阵Rot：

(6)

式中：c代表cos;s代表sin。

在动坐标系{A}中，动平台一点Ai的位置参数AAi(i=1,2,3)表示为：

(7)

式中：rA为动平台中心到各个支链顶端的距离。

在静坐标系{B}中，球铰Ci位置参数BCi(i=1,2)表示为：

(8)

式中：rB为静平台中心到各个支链顶端的距离；li(i=1,2)为平台边长。

动平台一点Ai位置参数BAi表示为：

BAi=Rot·AAi+P

(9)

式中：P=[x,y,z]T，[x,y,z]表示动平台原点在静平台下的位置矢量。

固定杆长矢量Li=BAi-BCi，i=1,2。

并联机构存在约束关系为：

(10)

式中：li(i=1,2)为动平台A2A3,A1A3矢量；Li(i=1,2)为PSR支链的S和R两副之间矢量长。

由式(10)可得支链1和2的杆长p1,p2为：

(11)

2.2 RUPR支链的运动逆解

用D-H法建立支链的坐标系，如图3所示，相应的D-H法参数见表1。表中：θi为运动副轴线的公法线间夹角；αi-1为运动副轴线间夹角；ai-1为被连接的运动副轴线公法线的长度；di为被连接的两条公法线的垂直距离；L3为R副和U副间的长度；p3为RUPR支链的U副和沿x3轴方向的R副间的长度。

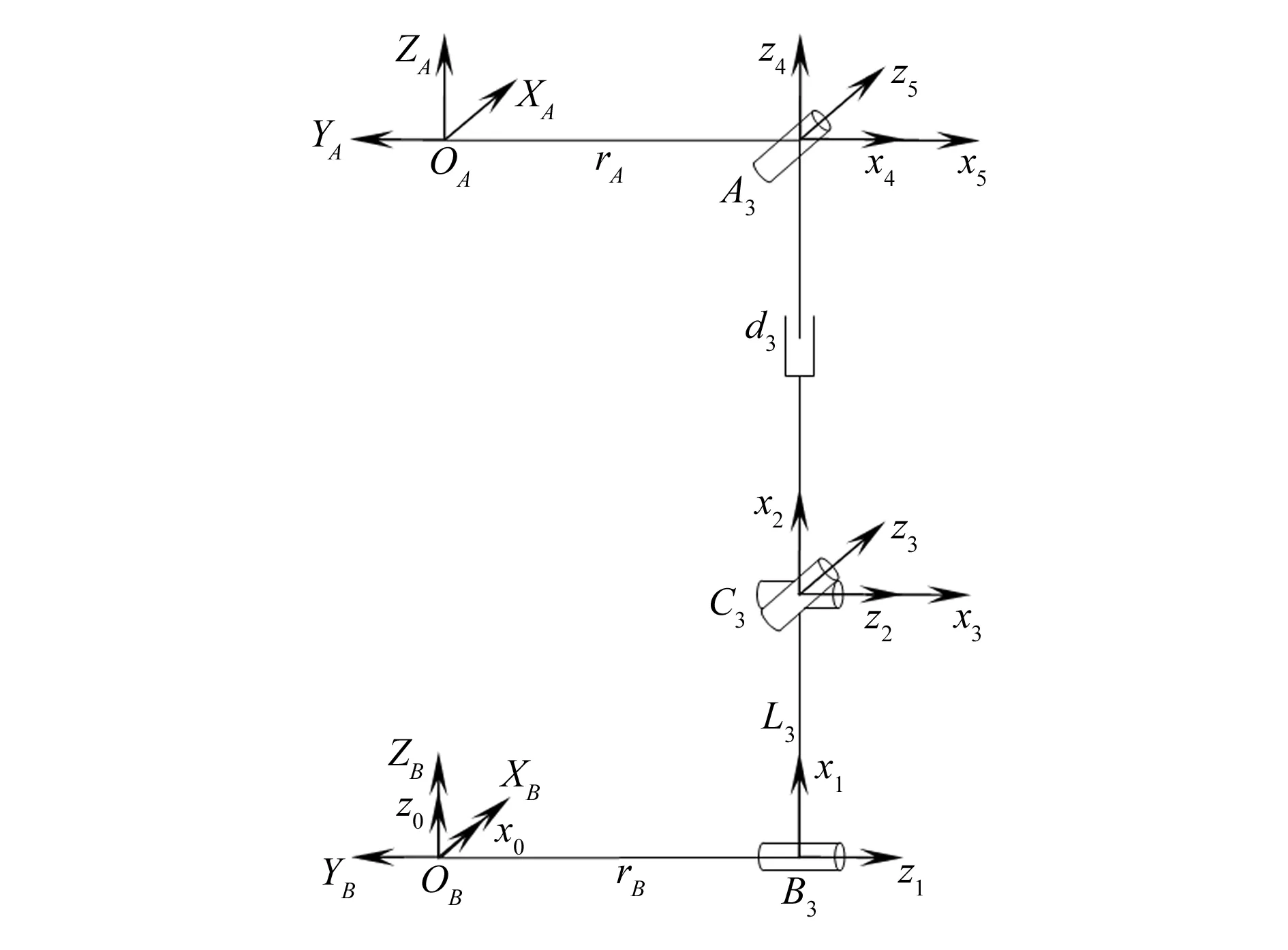
图3 RUPR支链坐标系

表1 RUPR的D-H表示

动平台OA到静平台OB的变换矩阵TOA-OB(x,θ1,θ2,θ3,θ5)可以写成：

式中:v(t)=cos(2π15t)为无噪声的真实信号;n(t)为随机信号,其均值为0,方差为0.6;e(t)为高斯脉冲信号.

Z-Y-X型欧拉角表示动平台的位姿矩阵为：

TOA-OB(x,y,z,γ,β,α)=

式中：变量(x,y,z,γ,β,α)为动平台的位姿参数。

通过比较Z-Y-X转换矩阵与动平台OA到静平台OB的变换矩阵，可以得到：

3 并联机构的工作空间分析

给定2-PSR/RUPR并联机构的一些参数：rB=60 mm,L1=L2=50 mm，rA=60 mm,L3=40 mm。通过在 MATLAB[10]中输入编写的程序和前面得到的逆解，得到可达工作空间，如图4所示。

图4 可达工作空间

由图4可知，该机构工作空间内部连续，空间范围也很大，验证了该机构有良好的运动性能，可以用于生产实践。

4 实例分析

本文设计了2-PSR/RUPR并联机构，通过在该并联机构的3个移动副上添加马达来驱动动平台的运动，通过调整动平台的位姿来获得不同的倾斜角度，从而对粘接不紧处进行上胶。不同倾斜角度盒体上胶的仿真结果如图5所示，验证了机构上胶的可行性。其中图5(a)、5(c)分别为并联机构绕XB轴和绕YB轴转动的上胶。

图5 不同倾斜角度盒体上胶的仿真结果

5 结束语

本文针对漏胶盒体，提出了一种上胶的2-PSR/RUPR并联机构。通过对2-PSR/RUPR并联机构进行三维建模，建立了螺旋理论下的运动螺旋系，得出机构可以实现沿ZB方向的平移以及绕XB轴和YB轴的转动。用MATLAB软件对机构进行仿真分析，绘制的工作空间没有出现空洞的情况，说明机构在各个方向上的运动连续且运动范围较大。本文的研究结果表明，2-PSR/RUPR并联机构结构简单，具有可调性，在发生包装盒漏胶情况时，可以进行不同倾斜角度下盒体的补胶，实现废品回收再利用。