基于非线性模型的柔性负荷方法研究

张晓晨，周文涛，刘 畅，陈 懿，杜孟珂，王泽黎

(国网北京朝阳供电公司，北京 100124 )

随着电力系统的不断发展，以可再生能源为基础的分布式发电(DG)设施不断完善，低压(LV)配电系统已广泛应用于工业、社会生活等各个方面。然而这些分布式发电可能存在风险，例如电流超过电缆线路极限导致过载，以及由于系统中注入大量能量而产生过电压。为此，需求响应(demand response，DR)成为有效集成这些分布式能源的一个非常合适的解决方案。

为了确保相关设备或设施处于最佳运行状态，目前国内外众多学者对需求响应进行了深入研究并制定了相应措施。卢锦玲等[1]根据多能源系统中的能量流动关系，对园区多能源系统内部各单元进行建模,并以系统运行总成本最小为目标，提出一种考虑电热负荷需求响应以及电动汽车接入的园区多能源系统优化运行策略。黄豫等[2]着重分析了能源互联网环境下的自动需求响应技术、储能技术、信息与通信技术，总结各需求响应技术未来的发展方向及面对的问题，并提出促进需求响应技术发展的多种建议。张军六等[3]重点研究了气电互联虚拟电厂多目标优化问题，构建了气电互联虚拟电厂多目标模型，通过为各目标函数赋权将多目标优化模型转化为单目标模型进行求解。Ramin等[4]提出了一个多目标随机网络约束机组组合(network constrained unit commitment，NCUC)问题，用于求解可移动电池储能(transportable battery-based energy storage，TBES)和DR规划，目的是最小化电网的运行成本和温室气体排放总量。Juan等[5]提出了一种基于价格的DR计划调度方案，目的是将用户的用电成本降到最低。然而大多文献只考虑平衡运行条件，这是比较片面的。

为解决上述问题，本文提出了应用于低压配电系统的柔性负荷模型，该模型为一个典型的非线性约束问题。

1 模型介绍

低压配电系统可看作是一个由多个节点与边构成的图G，描述为[6]

G=(V,E)

(1)

式中：V={v1,v2,…,vN}，为节点vr(r∈[1,N])的集合，其中N为节点数量；E={e1,e2,…,em}，为边et(t∈[1,m])的集合，其中m为边的数量。由于低压配电系统在径向配置下运行，因此系统具有树形拓扑结构。负荷以单相方式连接，且系统运行时通常处于负载不平衡状态。本文将每条单独的线路定义为四线线路，其中边em是三相加中性电缆的四元组，具体描述为

(2)

式中：a,b,c,n为四线线路，其中b为系统总线；k,j为线路中发送和接收节点(即电网中用户)，且∀k,j∈V；l为线路符号。

需注意，本文将次级变电站变压器的额定值用参考功率SB表示，同时将参考电压VB设置为标称线间电压(400 V)。

1.1 功率流模型

(3)

(4)

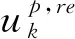
假设配电网系统接地良好，只考虑主要相位，故采用Kron简化[7]方法。令系统的状态变量为X，则X可通过求解非线性方程来确定。该方程描述了实际注入功率(sp)和计算注入功率(cal)之间的不匹配问题。此外，失配函数F(X)分为有功功率Fp(X)和无功功率Fq(X)两部分：

(5)

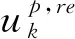
(6)

1.2 分布式光伏发电模型

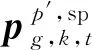
(7)

(8)

1.3 需求模型

(9)

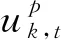
1.4 需求响应模型

(10)

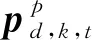
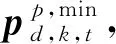
(11)

进一步，在能量方面，负荷转移是一种能源管理工具，负负荷转移(需求负荷减少)产生的能量必须等于正负荷转移(需求负荷增加)产生的能量。负荷转移可描述为特定时间框架内设备使用时间的变化，具体定义为

(12)

最后，负荷转移还受到与每个用户的功率pctd,k收缩百分比αk相关的操作限制：

(13)

式中：αk为固定值，用来限制负荷转移与用户功率关系。

2 柔性负荷模型与求解

2.1 柔性负荷模型

本文提出的柔性负荷方法是基于将需求响应机制作为一个控制变量引入到一个不平衡的三相最优功率流中，这就产生了一个非线性规划问题，该问题的限制条件为需求机制(公式(11)～(13))，目标函数OF为在日前时间t内找寻满足系统约束所需的总负荷，具体描述为：

(14)

2.2 模型求解

本文使用粒子群优化算法(particle swarm optimization，PSO)求解非线性规划问题。粒子群优化算法是一种典型的进化计算技术，其基本思想是通过群体中个体之间的协作和信息共享来寻找最优解。

PSO算法流程如图1所示。在每一次迭代过程中，粒子的速度和位置更新公式如下：

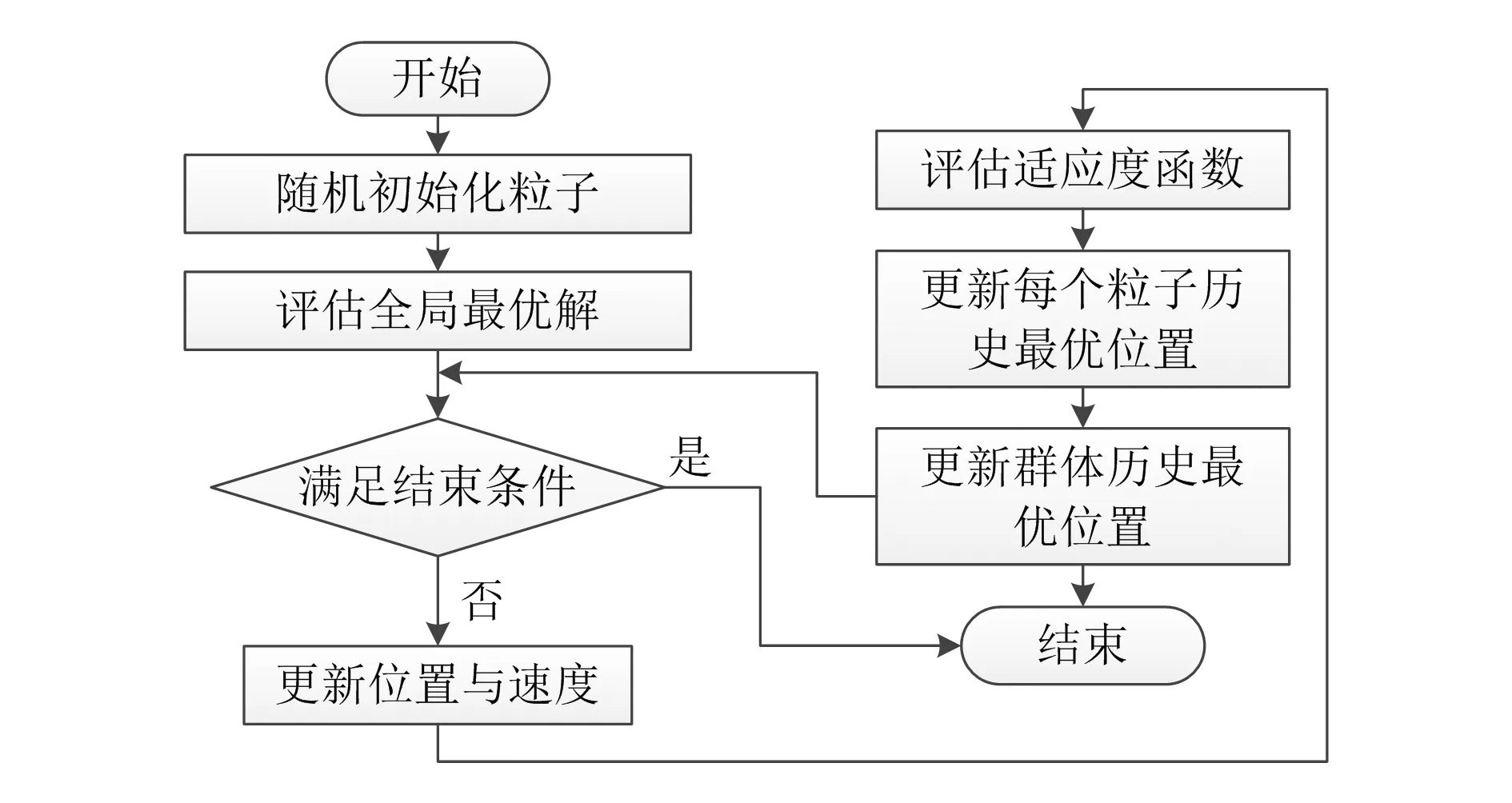
图1 PSO算法流程

vi=vi+c1+c2×rand()×(gbesti-xi)

xi=xi+vi

(15)

式中:i=1,2,…,h,为粒子，h为粒子总个数；vi为粒子速度；xi为粒子位置；rand()为0和1之间的随机数；c1,c2为学习因子；gbesti为第i个粒子的全局最优解。

3 仿真分析

为验证本文提出的柔性负荷模型，参考文献[10]中低压馈线模型(如图2所示)，该馈线具有基于光伏的分布式发电的高渗透性。本文所选馈线由23个用户组成，以单相配置沿馈线成对连接。低压馈线模型中存在偶尔过电压和过载情况。此外，每个用户都有一个峰值功率为pPVk=4 kW的光伏设施(这意味着每个设施有16个面板，每个面板的峰值功率为250 W)，每个用户的合同需求功率为pctd,k={3,15} kW。该网络由一台额定功率为800 kVA的二次变电站变压器统一管理。需求响应控制参数取如下值：βk∈(0.05,0.1)和αk∈(0.1,0.5)。

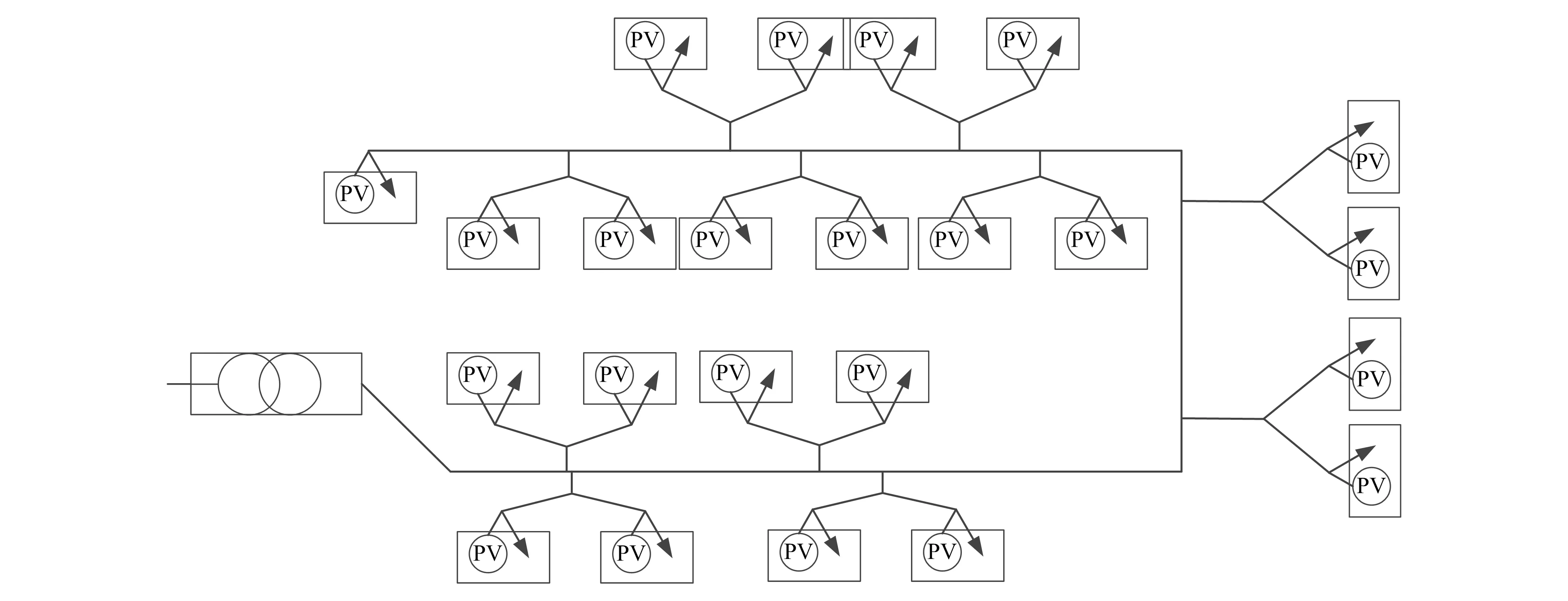
图2 低压馈线模型

应用柔性负荷模型后，有需求响应和无需求响应的柔性负荷对比结果如图3所示。可以看出柔性负荷将需求从一天中的早、晚时间转移到中午，以吸收光伏发电机组注入的电力。此外，图3(c)、(d)表明电压和电流满足限制条件，因此电力系统得以恢复到正常运行状态，进一步验证了本文所提方法对于能源效率提升发挥了一定作用。

图3 柔性负荷对比结果

4 结束语

以可再生能源为基础的分布式发电已广泛应用于各行各业。然而由于电流过载以及系统中注入大量能量而产生的过电压将给人们的生活带来诸多不便，为此本文提出了非线性约束的柔性负荷模型，并通过PSO算法进行求解，从而解决了基于光伏发电的分布式发电机组在不平衡配电系统中的电压和电流问题。

未来研究方向可考虑高效能量储存(如电池或热能)，从而减少配电网能量损耗。