BER Analysis of NOMA with Max-Min Relay Selection

Meng Shen,Zihao Huang,*,Xianfu Lei,*,Lisheng Fan

1 School of Information Science and Technology,Southwest Jiaotong University,Chengdu 610031,China

2 School of Computer Science,Guangzhou University,Guangzhou 510275,China

Abstract: In contrast with orthogonal multiple access(OMA) technologies,non-orthogonal multiple access(NOMA)technology can achieve higher spectral efficiency and support more users simultaneously.Multiple relays can be deployed in NOMA networks,in order to combat fading and thus increase the transmission reliability.In the existing works on cooperative NOMA networks with multiple relays,the decoding error at the relays and the imperfect successive interference cancellation (SIC) are not taken into account simultaneously.In this work,we consider the bit error rate (BER) analysis of relay-aided NOMA networks,where max-min relay selection is employed.Particularly,closed-form BER expressions are derived for NOMA networks with Rayleigh fading,in the existence of the relay decoding error and imperfect SIC.The asymptotic BER performance is then obtained to provide some useful insights into the system design such as the diversity order.Finally,simulation results illustrate the correctness of the derived expressions.The presented results reveal the effects of imperfect SIC and relay decoding error on the performance of cooperative NOMA networks.

Keywords:NOMA;bit error rate; relay decoding error;imperfect SIC

I.INTRODUCTION

With the rapid development of Internet of Things(IoT)applications such as smart city,the current wireless transmission rate is difficult to meet the requirements.Compared with 4G wireless communication systems,5G communication systems have higher transmission rate,lower latency and higher connection density.In order to meet these requirements,new communication technologies are being investigated,which include millimeter-wave communication,full-duplex networks,device-to-device (D2D) communication,massive multiple-input multiple-output (MIMO) and non-orthogonal multiple access(NOMA),etc.

As a promising technology,NOMA can improve spectral efficiency and increase the number of supported users.The key principle of NOMA is to assign different transmit power levels to users to implement multiple access,where multiple users share the same resource block.At the receivers,the successive interference cancellation(SIC)is employed to recover the signal.The performance of NOMA has been investigated in [1–4].Specifically,in [3],the outage probability was investigated for partial hybrid automatic repeat request(HARQ)enabled NOMA networks under time-correlated Rayleigh fading channels.In[4],the resource allocation was optimized to maximize the throughput for the buffer-aided wireless powered uplink NOMA systems.On the other hand,cooperative transmission can further improve the communication reliability and increase throughput.Recently,relay-assisted NOMA has been considered in [5–7].The authors in [6]studied the outage performance of NOMA networks that employed two-stage relay selection (TRS) schemes,where decode-and-forward(DF) and amplify-and-forward (AF) protocols were adopted.These results show that the performance of TRS schemes with adaptive power allocation (PA)outperforms that of TRS schemes with fixed PA [5].Moreover,in[7],the mode selection was optimized to maximize the throughput for the buffer-aided NOMA relay networks with direct links.However,these above studies focus on the assumption that the perfect SIC process is implemented,which is not very practical.

Considering the effect of imperfect SIC,there are some existing studies that analyze the error performance of NOMA networks.In [8],the authors derived the bit error rate (BER) expressions of uplink two-user NOMA systems under additive white Gaussian noise(AWGN)channels,where the assumption of fixed channel coefficients was impractical.Inspired by this,the BER of NOMA networks under Rayleigh fading channels was analyzed in [9],where both uplink and downlink were considered.Furthermore,the BER expressions for visible light communication (VLC)NOMA networks for different modulation schemes were derived in[10].In[11],the pairwise error probability(PEP)performance of underlay cognitive radio NOMA systems with partial relay selection technique was derived.In addition,the BER was investigated for multi-user NOMA systems in Rayleigh fading channels in[12],where asymptotic BER expressions were attained for perfect SIC and the upper bound of BER was obtained for imperfect SIC.To the best of our knowledge,there are no previous works which deal with the BER of relay-assisted NOMA with max-min relay selection with the relay decoding error and imperfect SIC.

In this paper,we analyze the BER performance of relay assisted downlink NOMA systems with maxmin relay selection.The exact probability density functions (PDFs) are derived for each hop with dependent links,which is a generalization of the analytical method[13].In particular,the BER performance is obtained in closed-form,in the existence of the relay decoding error and imperfect SIC.Moreover,the asymptotic BER expressions at high SNR and the diversity order are derived.Finally,simulation and analytical results are demonstrated to illustrate the effect of the PA on the system BER,in the presence of imperfect SIC and relay decoding error.

The rest of this paper is given as follows.In Section II,the system model of the cooperative NOMA network is introduced.In Section III,closed-form BER expressions under imperfect SIC and relay decoding error are obtained.In Section IV,asymptotic BER expressions at high SNR are derived from which the diversity order is revealed.Simulation results and some useful insights are presented in Section V.Finally,Section VI concludes this paper.

II.SYSTEM MODEL

As depicted in Figure 1,this work considers a twouser downlink NOMA network consisting of one base station (BS) andKhalf-duplex relays.Direct links from the BS to the users are not available because of the shadow fading.The BS communicates with the users through the relays where the DF relaying protocol is adopted [14].Suppose that all nodes in the networks are equipped with only one antenna.We assume that all the channels in the networks suffer from independent and identically Rayleigh fading,and denotehi ～CN(0,σ2),gi,1～CN(0,σ2) andgi,2～CN(0,σ2)as the complex channel coefficients of the BS-ithrelay,theithrelay-user 1 and theithrelay-user 2 links,respectively.Users are classified in the light of their different quality of service (QoS) requirements.Specifically,user 2 is a higher priority device,such as a road flood warning.In contrast,user 1 is a delaytolerated device,such as a device for downloading a movie.

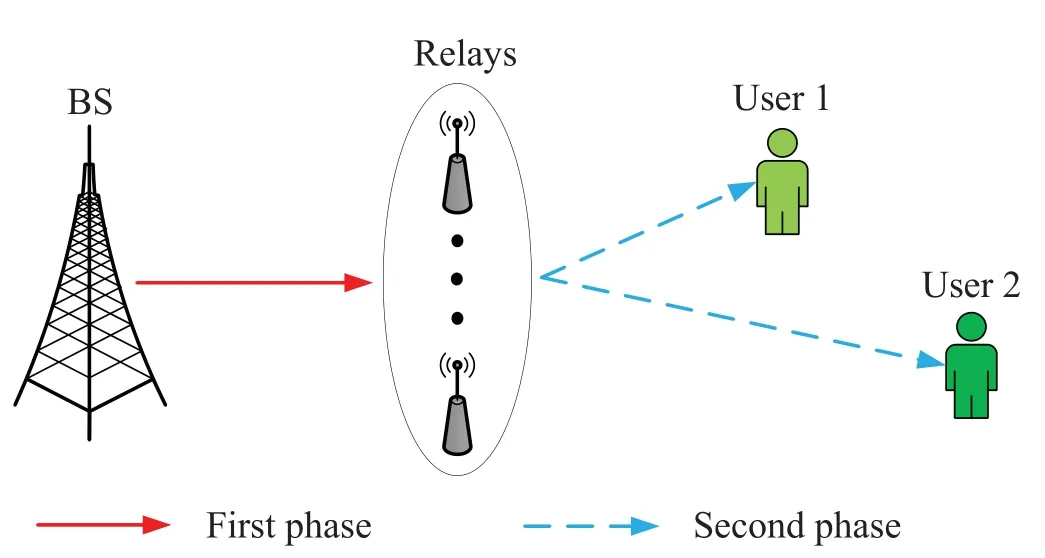
Figure 1.Downlink NOMA networks with multiple relays.

Max-Min relay selection[15]is adopted in this paper.Specifically,the relays overhear a ready-to-send(RTS) packet from the base station and two clear-tosend(CTS)packets from the user 1 and user 2.From RTS packet,the relay can estimate the instantaneous channel measurements from the base station to the relay.From CTS packets,the relay can estimate the instantaneous channel value from the relay to the user 1 and the instantaneous channel value from the relay to the user 2 according to the reciprocity theorem.When each relay receives the CTS packets,the timer will start.Because the timer is inversely proportional to the end-to-end channel quality,the best relay expires first.The expiring relay then sends a short duration flag packet to signal other relays of its existence.Other relays will keep silent after they receive this flag packet.This selection method is a distributed approach based on timers.Therefore,the relay selection criteria can be expressed as follows

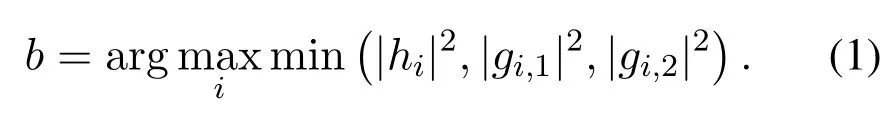
The total signaling takes two phases as follows.

The superimposed signal,√is transmitted from the BS to the selected relay in the first phase,wherexkis the transmitted signal to userk,andεkis the power allocation coefficient to thekth user.Note thatε1+ε2= 1 andε1< ε2since user 2 has higher service priority compared with user 1.Then,the observations at selected relay can be expressed as

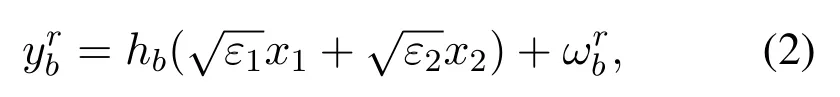
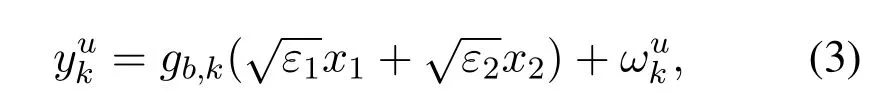
User 2’s receiver detectsx2by pretendingx1as interference.On the other hand,user 1’s receiver detectsx2first.The user 1’signal is then decoded after eliminating the regenerated user 2’signal from the received superimposed signal by applying SIC.

III.BER ANALYSIS

In this section,closed-form BER expressions of NOMA with max-min relay selection are derived.The constellation of superimposed signal at selected relay and users is illustrated in Figure 2.The first bit represents the signal of user 2 and the second bit represents the signal of user 1.Maximum likelihood detection(MLD)is adopt in identifying symbols.BPSK modulation is used for the whole transmission.For user 2,the decoding result of superimposed signal at selected relay has an significant effect on the decoding of user 2.Therefore,the error performance of user 2 is analyzed in four cases : 1) the selected relay decodes the two signals correctly;2)the selected relay detects user 2’signal correctly and user 1’signal erroneously;3) the selected relay detects user 1’ signal correctly and user 2’ signal erroneously; 4) the selected relay decodes both the signals erroneously.Considering all these cases,the user 2’s BER expressions can be expressed as

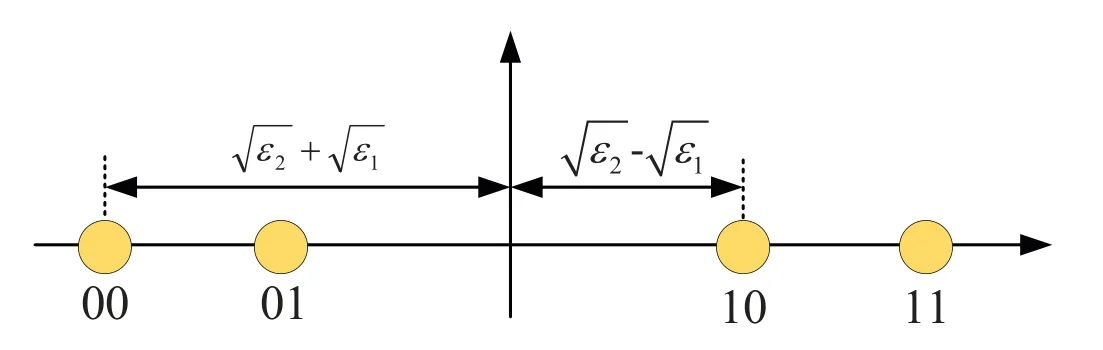
Figure 2.The constellation diagram.

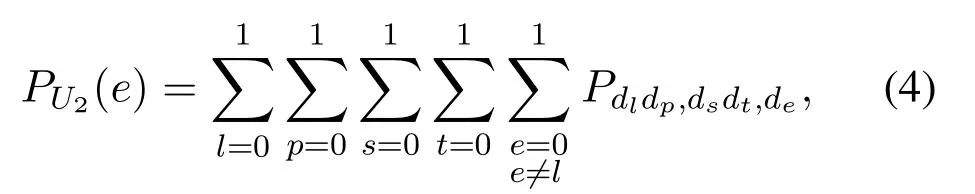
wherePdldpdsdtdedenotes the error probability of user 2 when the source sendsdldp,the relay decodes it todsdtand the user 2 decodes it tode.Moreover,d0=0,d1= 1.For example,when (00) is sent,andωrbis smaller thanthe selected relay can correctly decode both users’signals.Ifωu2is larger thanthe error will occur.By multiplying the prior probability,P00,00,1is written as

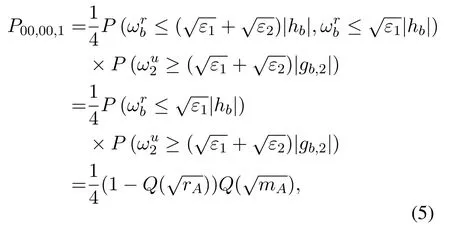
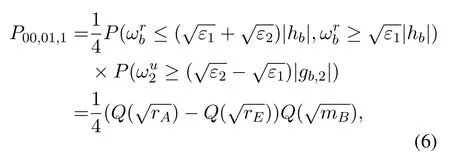
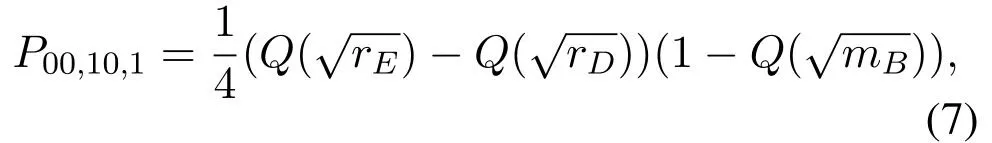
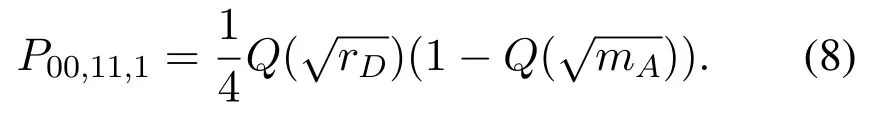
When(01)is sent,andωrbis smaller than−the selected relay will detect user 2’ signal correctly and user 1’ signal erroneously.Ifωu2is larger thanthe error will occur.By multiplying the prior probability,P01,00,1is obtained as

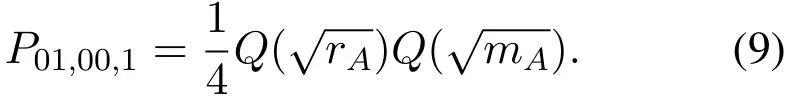
Ifωrbis smaller thanand exceedsthe selected relay will correctly decode both users’ signals.Ifωu2is larger thanthe error will occur.By multiplying the prior probability,P01,01,1is written as

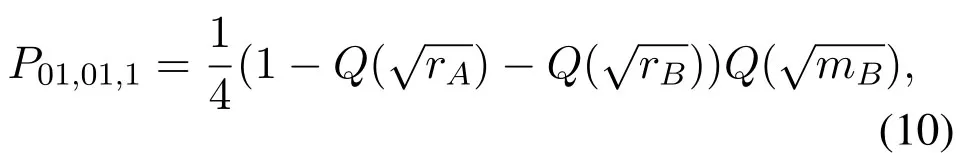
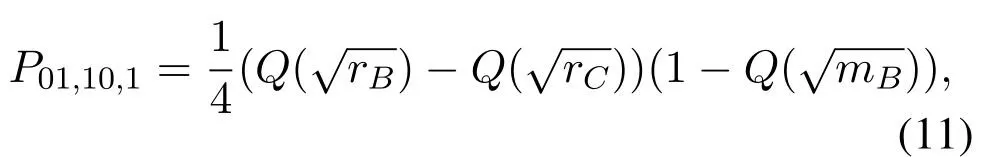
Because of symmetry,the BER can be easily obtained when the source sends 00 and 11.Therefore,the BER for the user 2 by the selected relay is presented in(15),whereQ(·)denotes the GaussianQfunction.

For user 1,the error probability is interfered not only by relay decoding error but also by imperfect SIC of the user 1’s receiver.We need to consider whether the decoded symbols of users at the selected relay are correct and whether the SIC is perfect.Therefore,the error performance of user 1 should be analyzed in eight cases.Considering all possible cases,the error probability of user 1 with the selected relay is given by

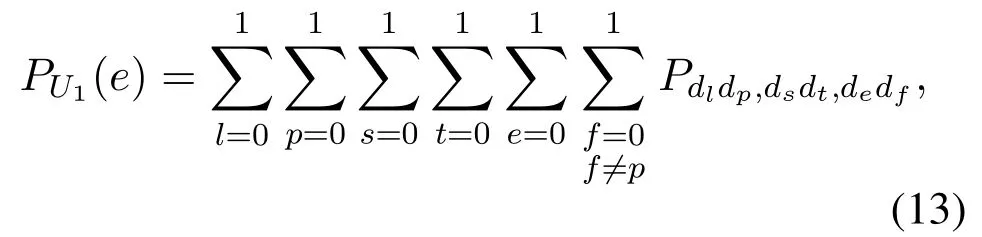
wherePdldp,dsdt,dedfdenotes the error probability of user 1 when the source sendsdldp,relay decodes it todsdtand user 1 decodes it todedf.For example,when(00) is sent,andωrbgoes beyondthe selected relay will erroneously decode both users’signals.When the selected relay sends (11),andωu1is larger thanSIC will be perfect.Meanwhile,ifωu1is larger thanthe error will occur.By multiplying the prior probability,P00,11,11is derived as

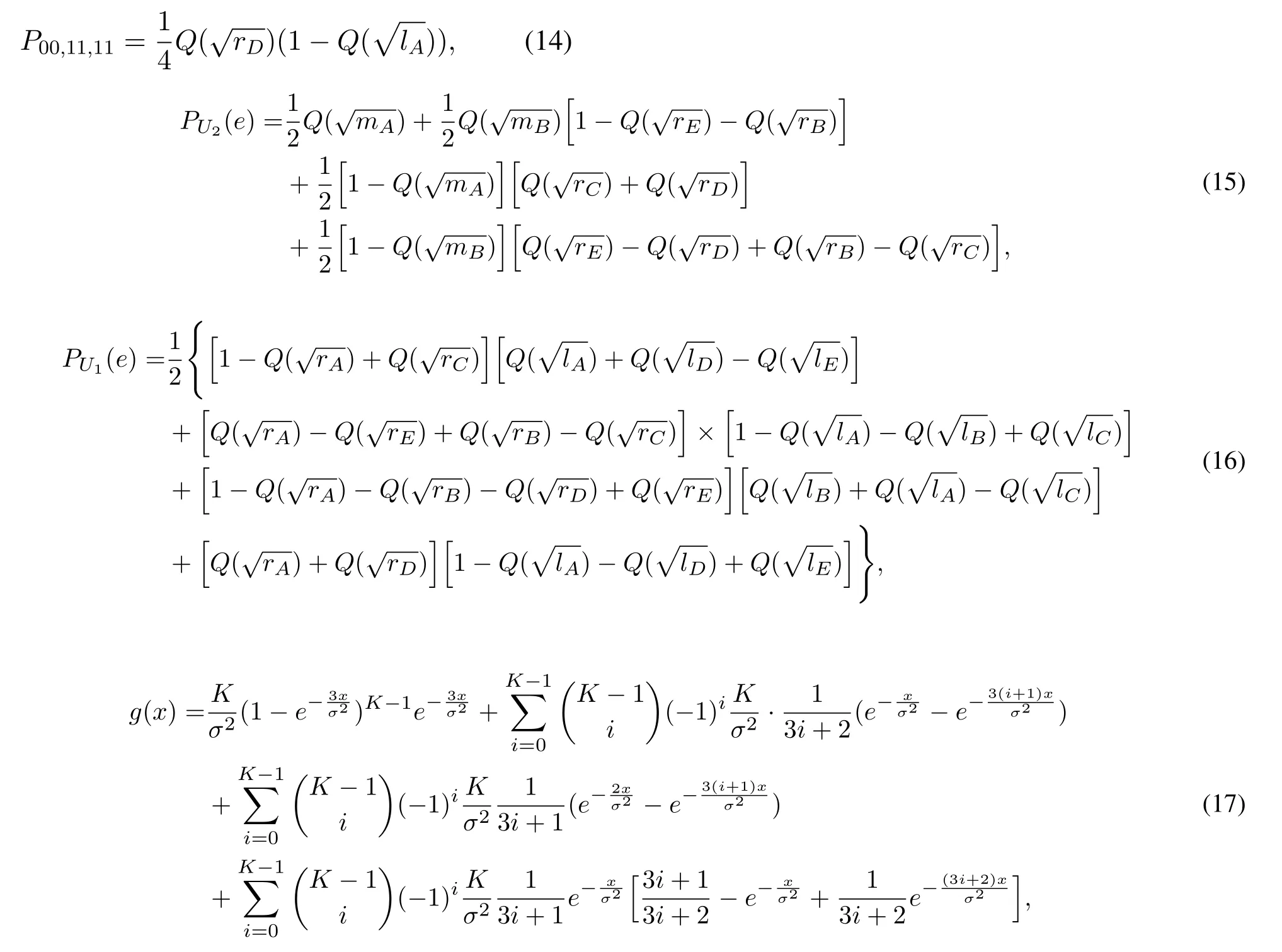
SIC will be imperfect.Meanwhile,ifωu1is larger thanthe error will occur.By multiplying the prior probability,P00,11,01can be written as

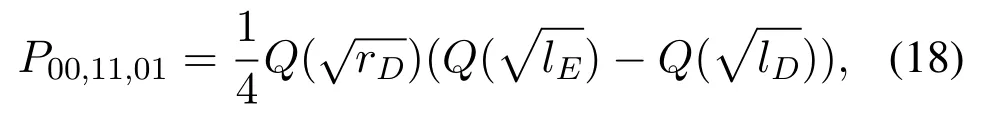
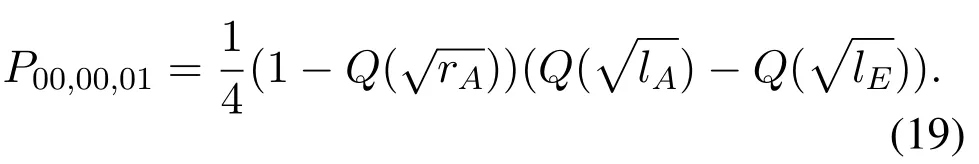
When the selected relay sends (00),andωu1is larger thanSIC will be imperfect.Meanwhile,ifωu1is larger thanthe error will occur.By multiplying the prior probability,P00,00,11is derived as

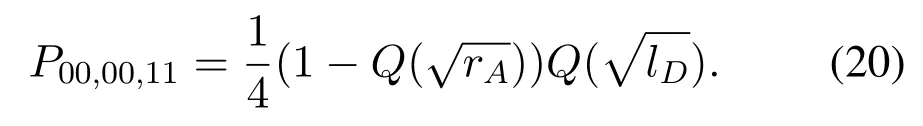
Ifωrbis smaller thanandωrbis higher thanthe selected relay will detect user 2’

signal correctly and user 1’ signal erroneously.When the selected relay sends(01),andωu1is smaller thanSIC will be perfect.At the same time,ifωu1is larger thanthe error will occur.By multiplying the prior probability,P00,01,01is given as

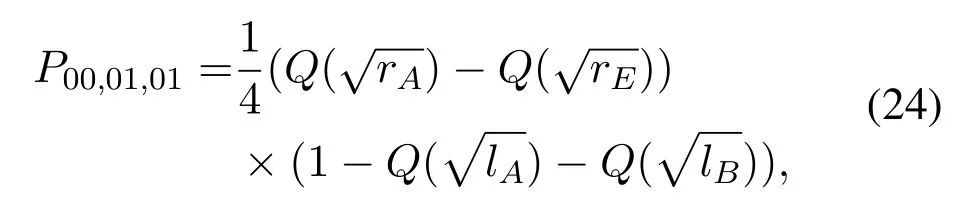
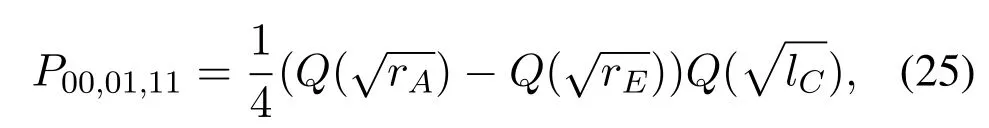
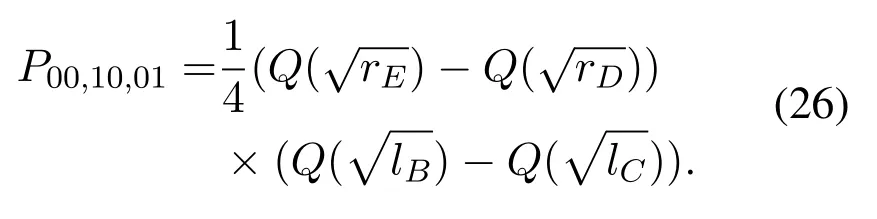
When the selected relay sends (10),andωu1is larger thanSIC will be perfect.Meanwhile,ifωu1is larger thanthe error will occur.By multiplying the prior probability,P00,10,11is given as

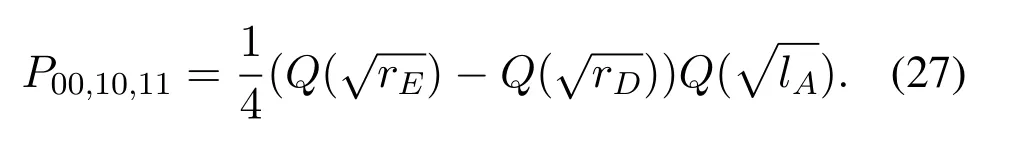
Similarly,the BER can be obtained when the source sends 01,10 and 11.Therefore,the error probability of user 1 with the selected relay can be calculated as in(16),shown at the top of the previous page.

SinceQ(·)is usually very small,we can have

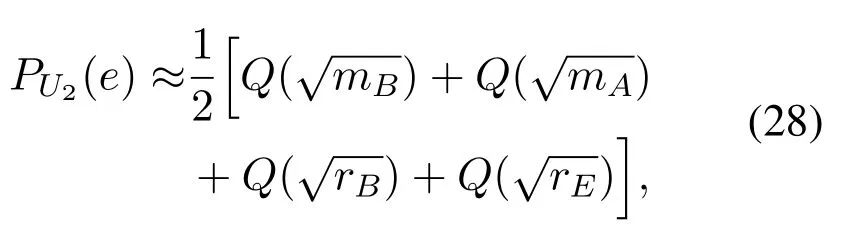
and

Under the assumption of independent and identically distributed links in the system,|hb|2,|gb,1|2and|gb,2|2are identically distributed,whose pdf is given by(17)(see Appendix for the proof).

Theorem 1.The average BERs of user 1 and user 2 are given by(21)and(22),respectively,at the top of the previous page,whereand f(x)are shownin(23).

Proof.With the aid of [16,Eq.(13)],by substituting(17)into(28),and then by substituting(17)into(29),we can complete the proof of this Theorem.

Since the analytical BER expressions in (28) and(29) are composed of elementary functions only,we can readily evaluate the BER performance for the considered system.

IV.ASYMPTOTIC BER ANALYSIS

To obtain more useful insights into the system design,we further study the asymptotic BER performance for the considered system in the high regime of SNR.The asymptotic BER can be used to reveal the achieved diversity order,which is defined as:

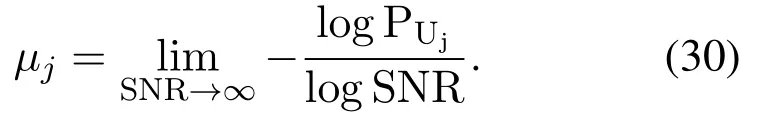
The asymptotic BERs performance of user 1 and user 2 are presented in the following theorem,

Theorem 2.The asymptotic BERs of user 2 and user 1 can be obtained as

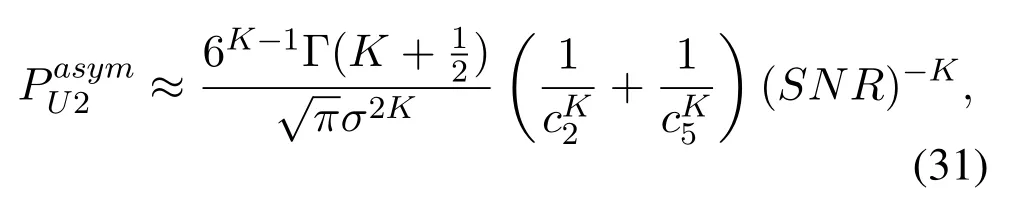
and

Proof.whenSNR →∞,g(x)can be approximated by

Substituting (33) into (28) and (29),the asymptotic BERs of user 1 and user 2 can be obtained,respectively.The proof of Theorem 2 is completed.

Based on Theorem 2,the diversity order of user 2 and user 1 are given by

This indicates that the proposed scheme can achieve the full diversity order ofK,through exploiting the performance gain by the multiple relays in the system.Clearly,the system performance can be rapidly enhanced by increasing the number of relays.

V.SIMULATION RESULTS

In this section,Monte Carlo simulation results are provided to verify the correctness of the derived BER expressions and illustrate the impact of imperfect SIC and relay decoding error.In all simulations,the variance of the Rayleigh channels is assumed to beσ2=0.2.

Figure 3 plots the BER performance versus SNR forK= 1 and 2.Obviously,one can notice that the analytical results are in perfect agreement with the simulation results.Moreover,the BER performance of user 2 outperforms that of user 1,since SIC error and less transmit power dominate the error performance compared to the interference from user 1.It can be also seen that the BER gap between user 1 and user 2 in Figure 3b becomes larger for different numbers of relays.This indicates that it is necessary to investigate the effect of power allocation on the error performance of users.Moreover,we find that the BER performance gets better when the number of relays increases.The asymptotic BER of the two users are also depicted in Figure 3.Furthermore,the diversity orders of both users are equal toK,which verifies the analytical result in(34).

Figure 3.Effect of number of relays on the BER where ε1 =0.3,ε2 = 0.7 in (a) and ε1 = 0.15,ε2 = 0.85 in (b),respectively.

Figure 4 shows the effect of the power allocation coefficient on the BER of users.As observed from Figure 4,one can find that as the power allocation coefficient increases,the error performance of user 2 degrades because of the less transmit power.As the power allocation coefficient increases,the error performance of user 1 becomes better first and then worse.This is because that the error performance is dominated by the error propagation instead of transmit power.Also,we find that the BERs of user 1 and user 2 are equal when the power allocation coefficient exceeds a threshold.This suggests that the impact of imperfect SIC and interference on the user’s BER is equal.Moreover,an optimum power allocation coefficient can be observed.For example,whenSNR= 30dBand user 2’ BER is below 10−3,the optimal power allocation coefficient is 0.2 forK= 2 andK=3.

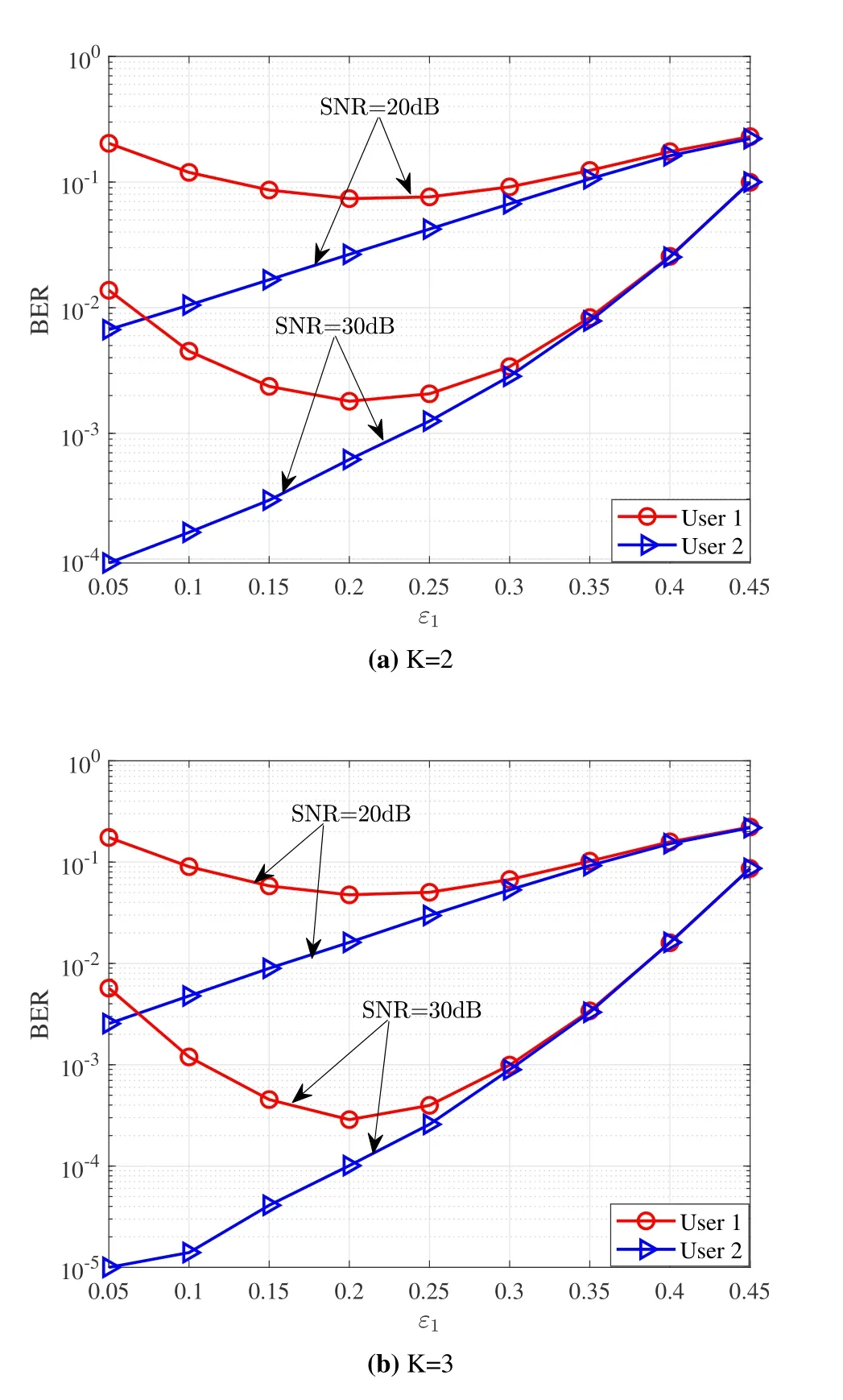
Figure 4.Effect of the power allocation coefficient on the error performance of users.

Figure 5 shows the effect of error propagation on the BER of users,whereε1=0.3 andε2=0.7.In particular,Figure 5a and Figure 5b correspond to user 1 and user 2,respectively.It can be observed that there is a significant performance gap between relay decoding error with imperfect SIC and relay perfect decoding(cyclic redundancy check-aided)with perfect SIC.For example,in Figure 5a,when BER is 10−2,the difference is about 5.5 dB.

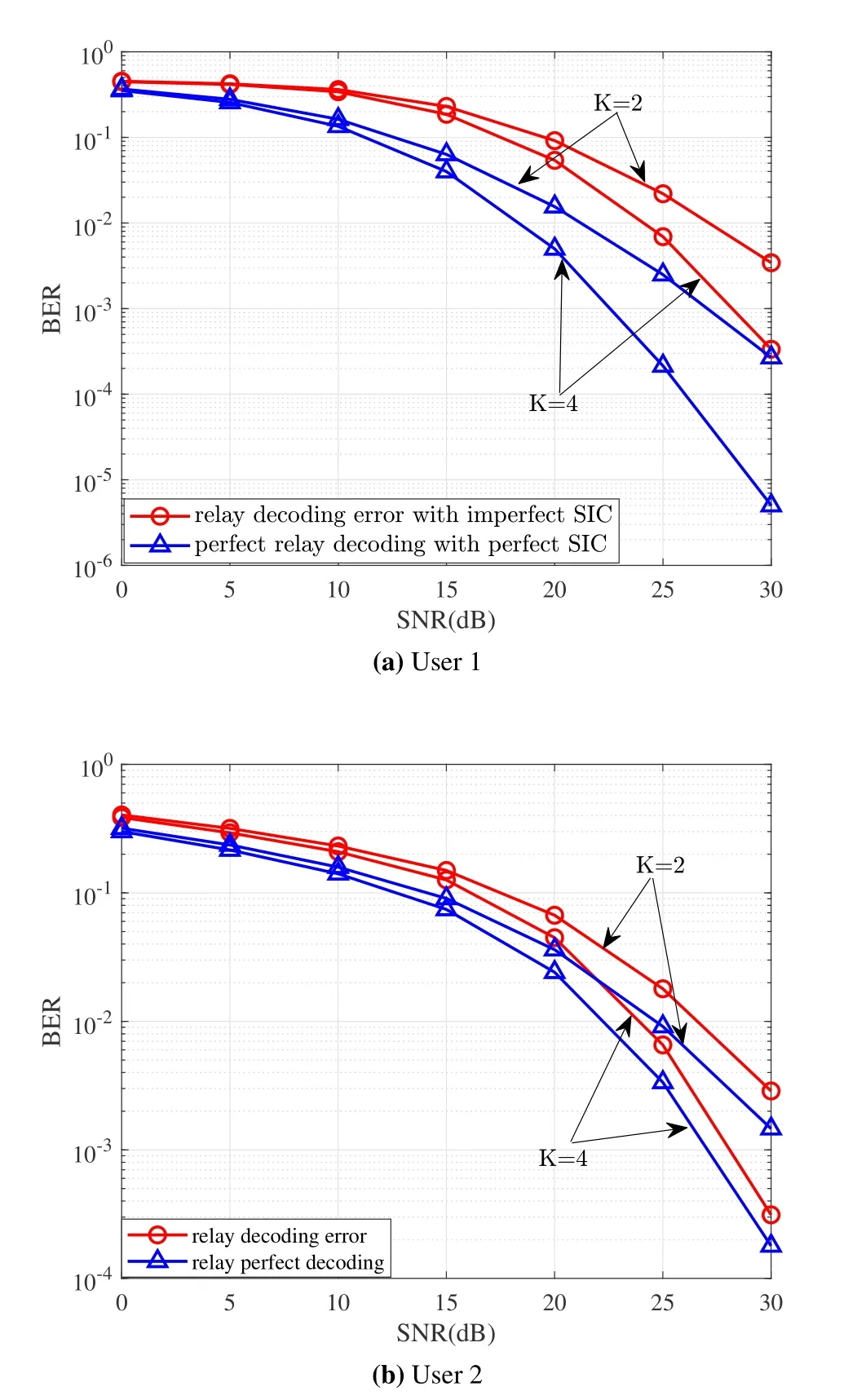
Figure 5.Effect of error propagation on the error performance of users.

VI.CONCLUSION

In this work,closed-form BER expressions for relayassisted NOMA networks with max-min relay selection have been derived over Rayleigh fading channels,in the existence of the relay decoding error and imperfect SIC.Moreover,the asymptotic BER performance was obtained,which can be used to evaluate the system diversity order.Through the simulation results and theoretical analysis,it has been shown that the imperfect SIC and relay decoding error can have a severe effect on the error performance of users.

ACKNOWLEDGEMENT

This work was supported by the National Natural Science Foundation of China under Grants 61971360 and 61871139.

APPENDIX

Define|hb|2=X,|gb,1|2=Y,|gb,2|2=Z,then the joint CDF of channel gains associated with the best relay is given by

After taking the derivative,the joint PDF is given by

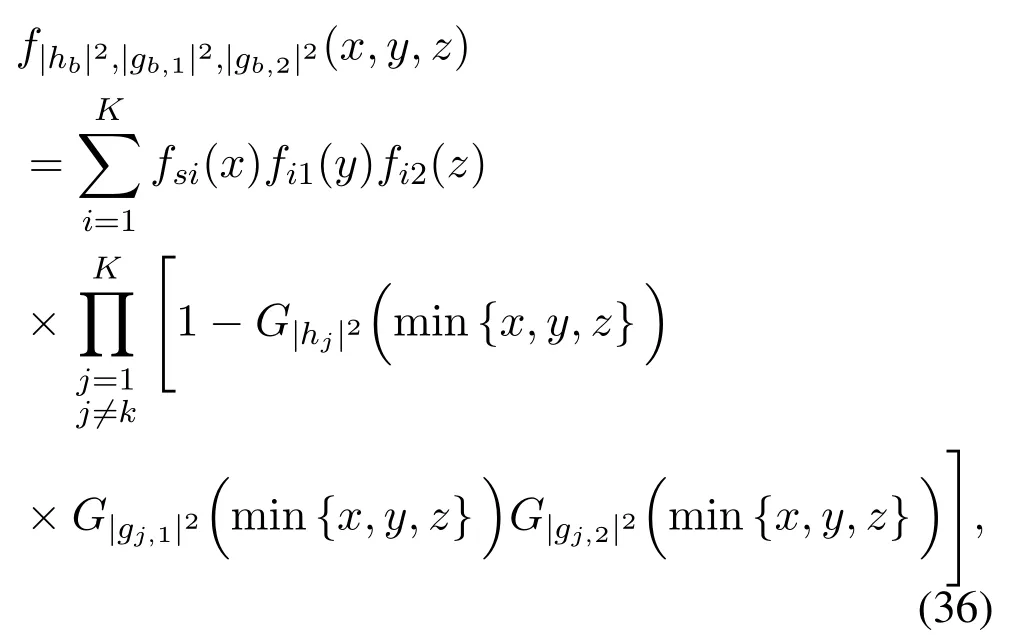
whereG|hj|2(·),G|gj,1|2(·)andG|gj,2|2(·)are the complementary cdfs(ccdfs)of|hj|2,|gj,1|2and|gj,2|2,respectively,andfsi(·),fi1(·),fi2(·)refer to the pdfs of the BS-ithrelay,theithrelay-user 1 and theithrelayuser 2 links,respectively.As all links in the networks are identically distributed,we can further have,

Hence,

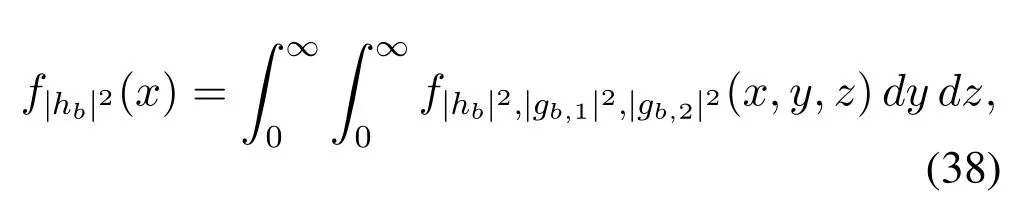
and

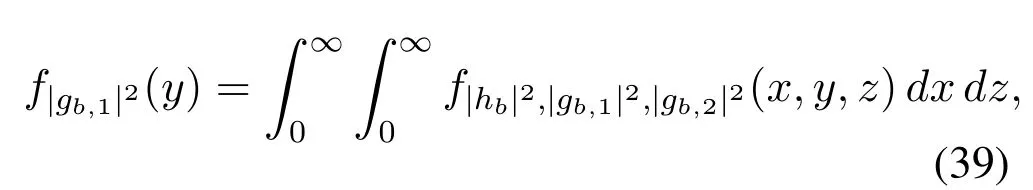
and

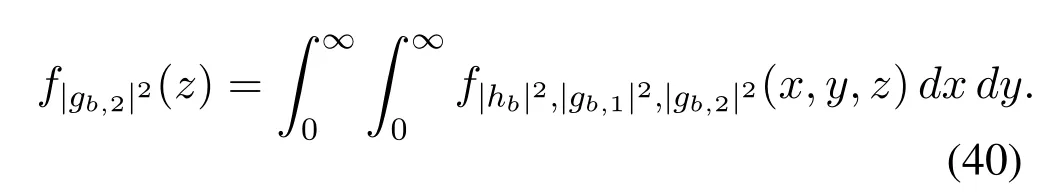
Evaluating the integrals of (38),(39) and (40),the proof is completed.