关于模糊映射的LgH-方向可微性问题的研究
李婷婷,包玉娥
(内蒙古民族大学 数理学院,内蒙古 通辽 028043)
关于模糊映射的可微性问题的研究中,有利用模糊数的H-差运算[1]给出的H-可微性概念[2]和利用模糊数的gH-差运算[3]给出的gH-可微性概念[4].2003年,WANG等[5]给出了模糊映射的H-方向可微性概念,研究了凸模糊映射的方向导数的刻划和存在性问题.2013年,BEDE等[4]给出了模糊映射的gH-可微性和LgH-可微性(gH-截可微性)概念及一系列相关性质,讨论了模糊映射的gH-可微性与积分之间的关系.文献[6]和文献[7]分别讨论了区间值映射的gH-方向可微性和模糊映射的gH-方向可微性问题,给出了区间值映射的gH-方向可微性概念和模糊映射的gH-方向可微性概念,得到了一些有意义的结论.在此基础上,给出了模糊映射的LgH-方向可微、LgH-偏导数和LgH-梯度的概念,讨论了模糊映射的LgH-方向可微性与区间值映射的gH-方向可微性以及端点函数的方向可微性之间的关系,证明了模糊映射的LgH-导数和LgH-偏导数均为模糊映射沿坐标轴方向的LgH-方向导数.
1 预备知识
定义1.1[8]设R为实数集,如果模糊集u:R→[0,1]满足下列4个条件:
(1)u是正规模糊集,即存在x∈R使得u(x)=1;
(2)u是上半连续函数;
(3)u是凸模糊集,即对任意的x,y∈R,λ∈[0,1],有
(4)u的承集是紧集.
则称u为R上的模糊数,记ℱ为R上的所有模糊数构成的集合(即模糊数空间).对u∈ℱ,u的α-截集(α∈[0,1])是一个有界闭区间
对于u,v∈ℱ及r∈R,模糊数空间ℱ上的加法运算和数乘运算定义如下:
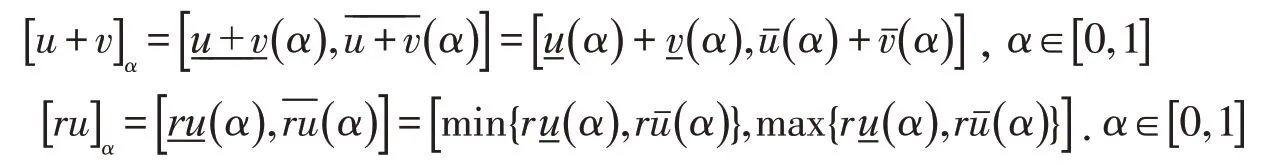
对于u,v∈ℱ,采用的u与v之间的距离公式为
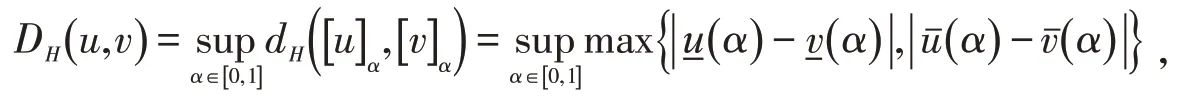
设M为Rn中的一个非空子集.将M到ℱ的映射称为模糊映射,记为F:M→ℱ.对α∈[]0,1,可以得
到与模糊映射F:M→ℱ相对应的一族区间值映射x∈M.
其中,(1)[R]表示R上的所有有界闭区间构成的区间数空间;
定义1.2[3]对于u,v∈ℱ,如果存在w∈ℱ,使得u=v+w或v=u+(-1)w,则称u与v的广义H-差(即gH-差)存在,记为w=u⊖gHv.
如果u⊖gHv存在,则对α∈[]0,1,有
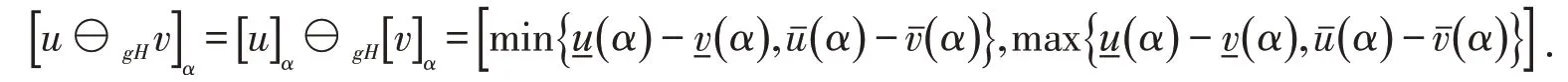
性质1.1[3]对于,如果ugHv存在,则对r∈R,有ru⊖gHrv也存在,且
对y∈Rn,记ye为y的单位向量.
定义1.3[7]设为模糊映射,x∈M.如果对y∈Rn,存在δ>0,使得对任意h∈()0,δ,有x+hye∈M(x-hye∈M)且gH-差存在,同时存 在使得
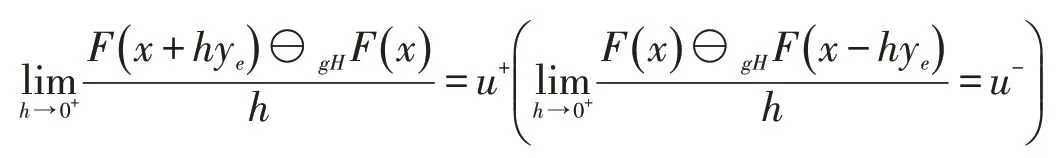
则称F在x处沿y方向右(左)gH-方向可微,称u+(u-)为F在x处沿y方向的右(左)gH-方向导数,并记为
定义1.4[6]设f:M→[R]为区间值映射,x∈M.如果对y∈Rn,存在δ>0,使得对任意h∈(0,δ),有且存在,使得
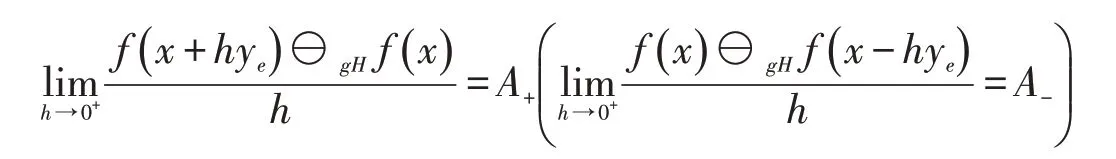
则称f在x处沿y方向右(左)gH-方向可微,并称A+(A-)为f在x处沿y方向的右(左)gH-方向导数,记为
定理1.1[6]设f:M→[R]为区间值映射,.如果f在x处沿y方向gH-方向可微,并且存在δ>0,使得对h∈(0,δ),有则,其中和分别为和在x处沿y方向的方向导数.
定义1.5[4]设F:(a,b)→ℱ为模糊映射,x∈(a,b)且x+h∈(a,b).如果存在u∈ℱ,使得
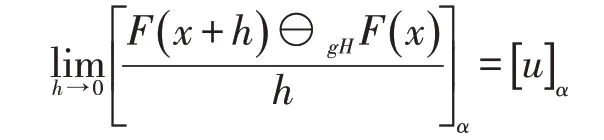
则称F在x处LgH-可微,且u称为F在x处的LgH-导数,并记为FLgH(x)=u.
2 主要结果
定义2.1设F:M→ℱ为模糊映射,x∈M.如果对y∈Rn,存在δ>0,使得对h∈(0,δ),有x+hye∈M(x-hye∈M)且gH-差存在,同时存在u+∈ℱ(u-∈ℱ)使得对α∈[0,1]有
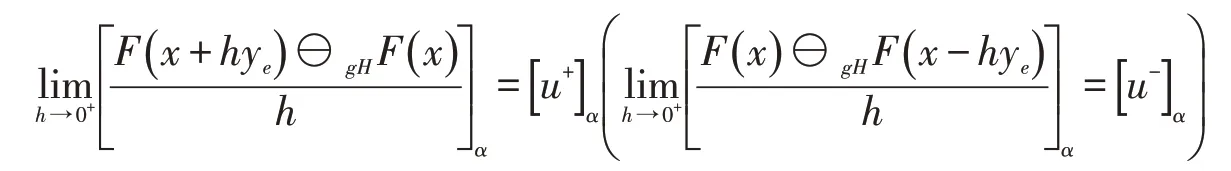
则称F在x处沿y方向右(左)截gH-方向可微(简记为LgH-方向可微),称u+(u-)为F在x处沿y方向的右(左)截gH-方向导数,并记为
定理2.1设F:M→ℱ为模糊映射,x∈M,y∈Rn.
(1)如果F在x处沿y方向右(左)gH-方向可微,则F在x处沿y方向右(左)LgH-方向可微且
(2)如果F在x处沿y方向gH-方向可微,则F在x处沿y方向LgH-方向可微且
证明(1)设F在x处沿y方向右(左)gH-方向可微,则对x∈M,y∈Rn,存在δ>0,使得对h∈(0,δ),有x+hye∈M(x-hye∈M)且gH-差存在,同时存在,使得对α∈[0,1]有
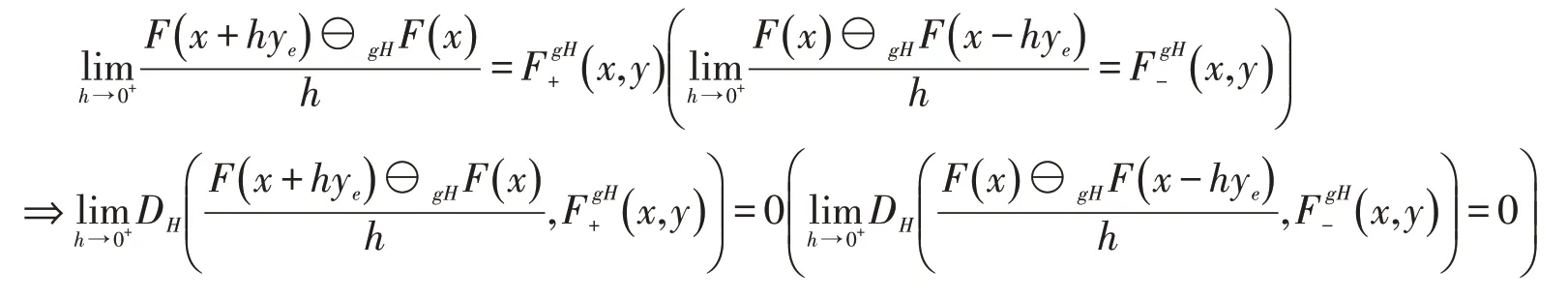
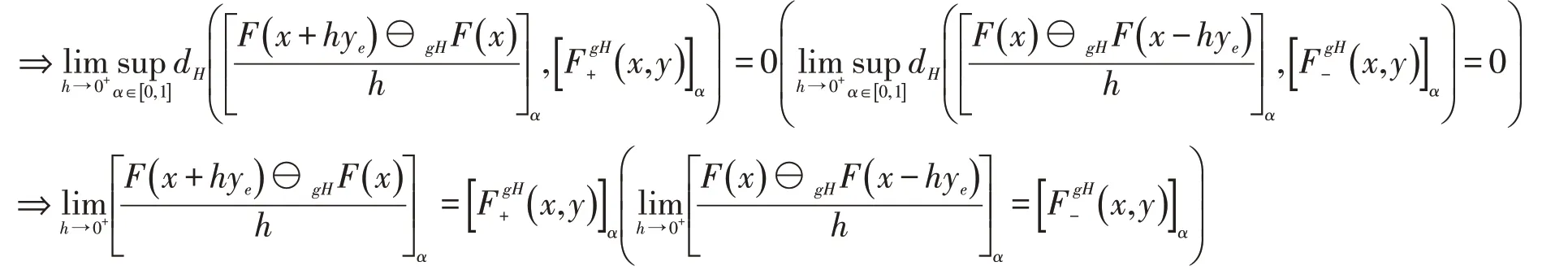
所以,根据定义2.1可得F在x处沿y方向右(左)LgH-方向可微且
(2)设F在x处沿y方向gH-方向可微,则有.又 由(1)知.于是有.所以,F在x处沿y方向LgH-方向可微且
定理2.2设F:M→ℱ为模糊映射,x∈M,y∈Rn,α∈[0,1].
(1)如果F在x处沿y方向右(左)LgH-方向可微,则区间值映射Fα:M→[R]在x处沿y方向右(左)gH-方向可微且
(2)如果F在x处沿y方向LgH-方向可微,则区间值映射Fα:M→[R]在x处沿y方向gH-方向可微且
证明(1)设F在x处沿y方向右(左)LgH-方向可微,则对x∈M,y∈Rn,存在δ>0,使得对h∈(0,δ),有且gH-差存在,同时存在,使得对α∈[0,1]有
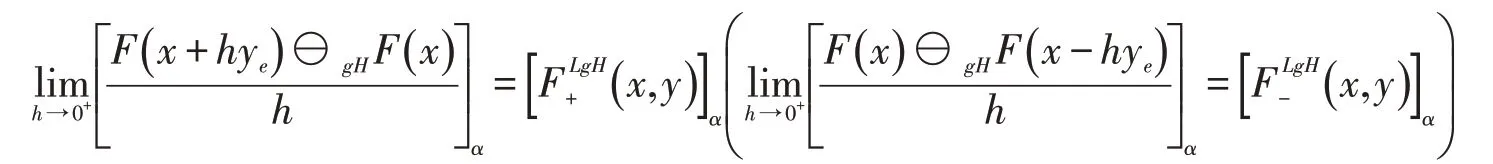
由定义1.2有
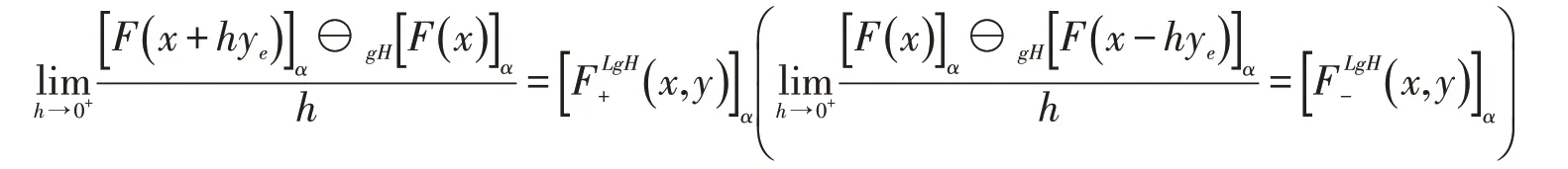
所以,根据定义1.4可得区间值映射Fα在x处沿y方向右(左)gH-方向可微且
(2)设F在x处沿y方向LgH-方向可微,则对x∈M,y∈Rn,存在δ>0,使得对h∈(0,δ),有,且gH-差存在,同时存在,使得对α∈[0,1]有
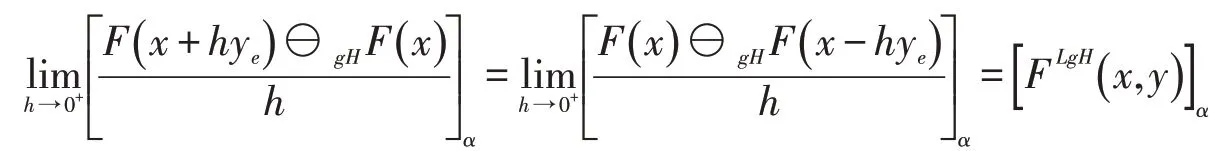
由定义1.2有
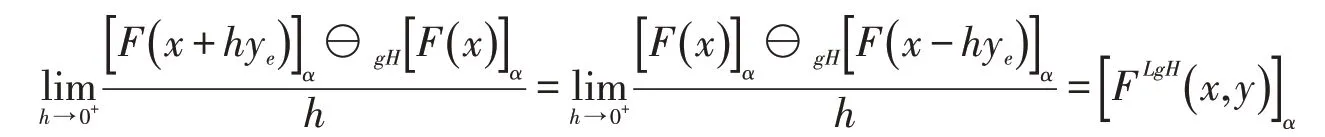
所以,根据定义1.4可得区间值映射Fα在x处沿y方向gH-方向可微且
定理2.3设F:M→ℱ为模糊映射,
(1)如果F在x处沿y方向右LgH-方向可微,并且存在δ>0,使得对h∈(0,δ),α∈[0,1]有,则区间值映射Fα的两个端点函数和在x处沿y方向的右方向导数均存在,并且,其中和分别为和在x处沿y方向的右方向导数.
(2)如果F在x处沿y方向左LgH-方向可微,并且存在δ>0,使得对h∈(0,δ),α∈[0,1]有,则区间值映射Fα的两个端点函数和在x处沿y方向的左方向导数均存在,并且,其中和分别为和在x处沿y方向的左方向导数.
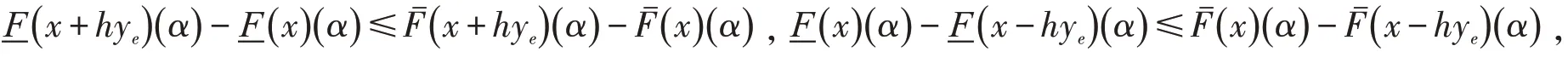
(3)如果F在x处沿y方向LgH-方向可微,并且存在δ>0,使得对h∈(0,δ),α∈[0,1]有则区间值映射Fα的两个端点函数和在x处沿y方向的方向导数均存在,并且,其中和分别为和在x处沿y方向的方向导数.
证明(1)设F在x处沿y方向右LgH-方向可微,则对x∈M,y∈Rn,存在δ>0,使得对h∈(0,δ),有x+hye∈M且gH-差存在,同时存在,使得对α∈[0,1]有
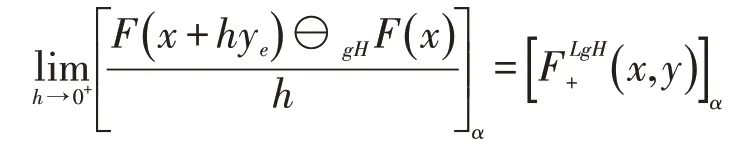
由定义1.2及性质1.1有
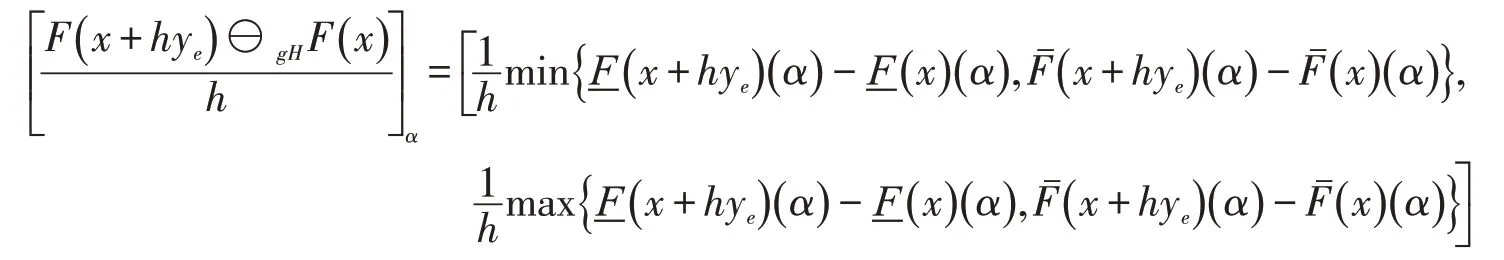
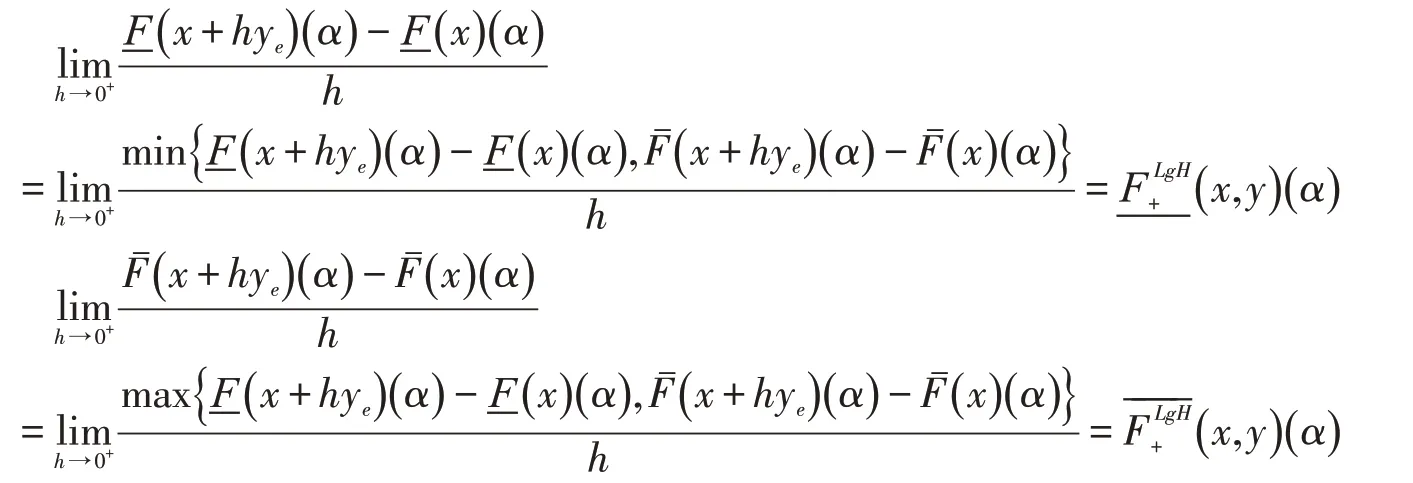
(2)和(1)的证明相同,从略.
(3)设F在x处沿y方向LgH-方向可微,则对x∈M,y∈Rn,存在δ>0,使得对h∈(0,δ),有x+hye,x-hye∈M且gH-差存在,同时存在,使得对α∈[0,1]有
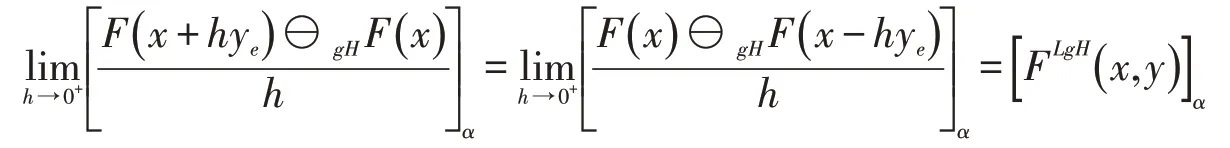
定理2.4设F:(a,b)→ℱ为模糊映射,则F在x处沿y=1方向LgH-方向可微当且仅当F在x处LgH-可微且FLgH(x)=FLgH(x,1).
证明必要性 设F在x处沿y=1方向LgH-方向可微,则存在δ>0,使得对h∈(0,δ),有x+h,x-h∈(a,b)且gH-差存在,同时存在FLgH(x,1)∈ℱ使得对α∈[0,1]有
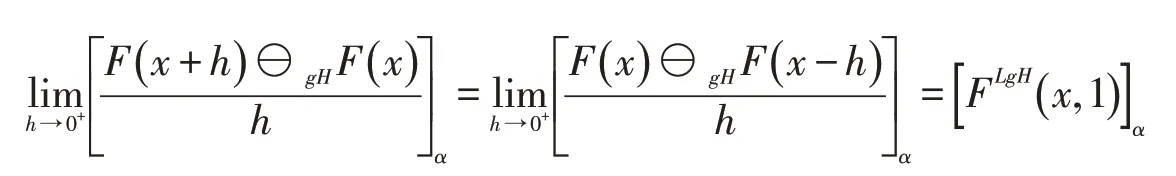
由于
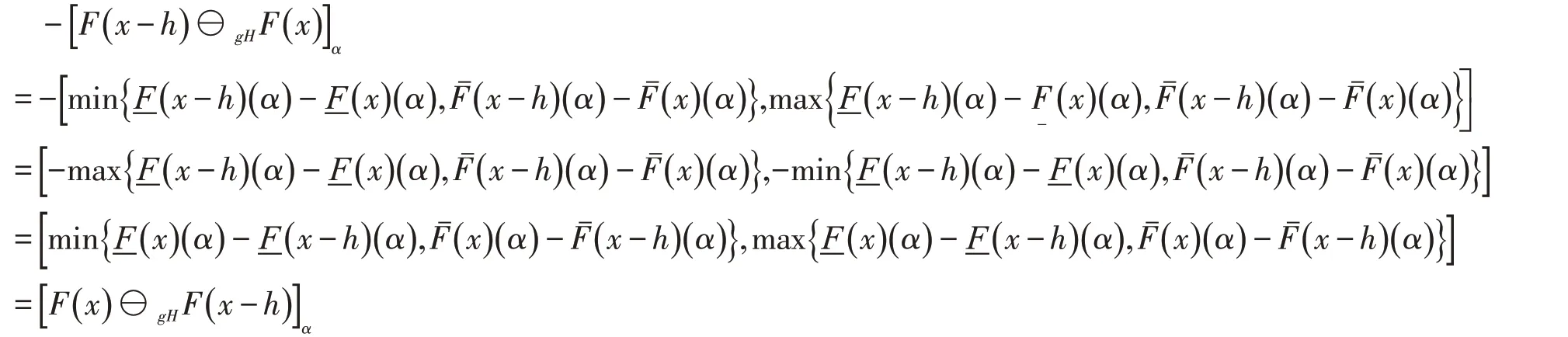
于是有
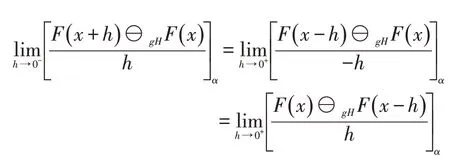
从而有
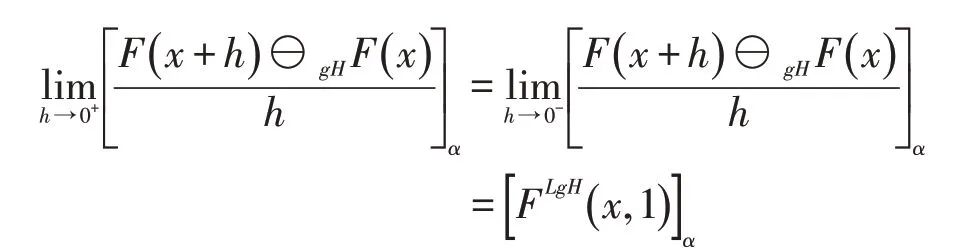
所以,根据定义1.5可得F在x处LgH-可微且
充分性 设F在x处LgH-可微,则存在,使得对α∈[0,1]有
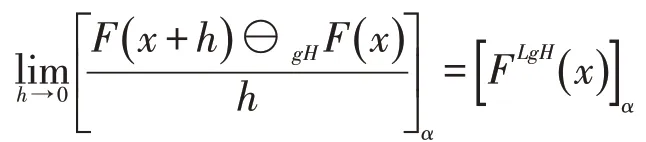
即存在δ>0,使得对h∈(0,δ),有x+h,x-h∈(a,b)且gH-差存在,由必要性的证明过程可知
于是有
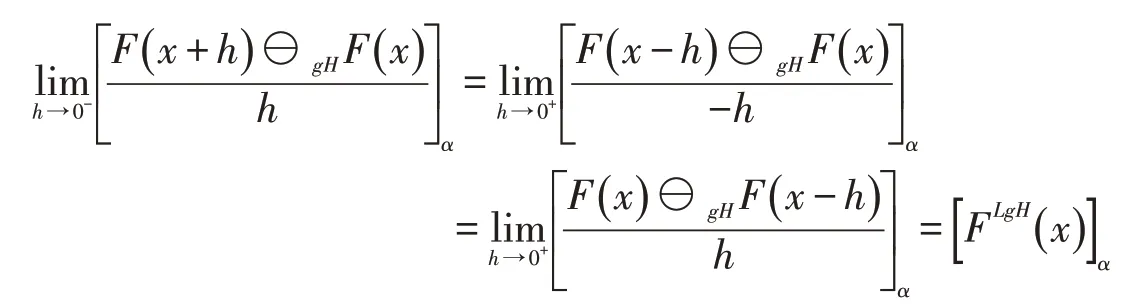
从而有
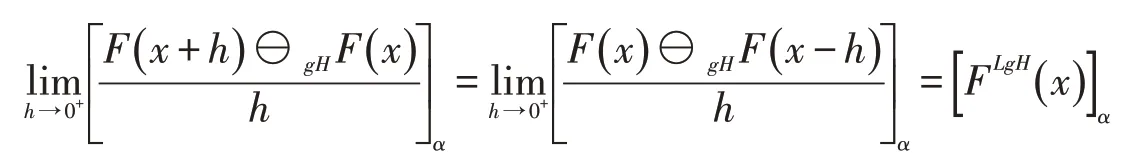
所以,根据定义2.1可得F在x处沿y=1方向LgH-方向可微且
定义2.2设F:M→ℱ为模糊映射,.如果模糊映射在xi处LgH-可微,则称F在x0处关于xi的LgH-偏导数存在,记为,且
定理2.5设F:M→ℱ为模糊映射,.如果F在x0处沿ei方向LgH-方向可微,则F在x0处关于xi的LgH-偏导数存在,且
证明设,则对α∈[0,1]有
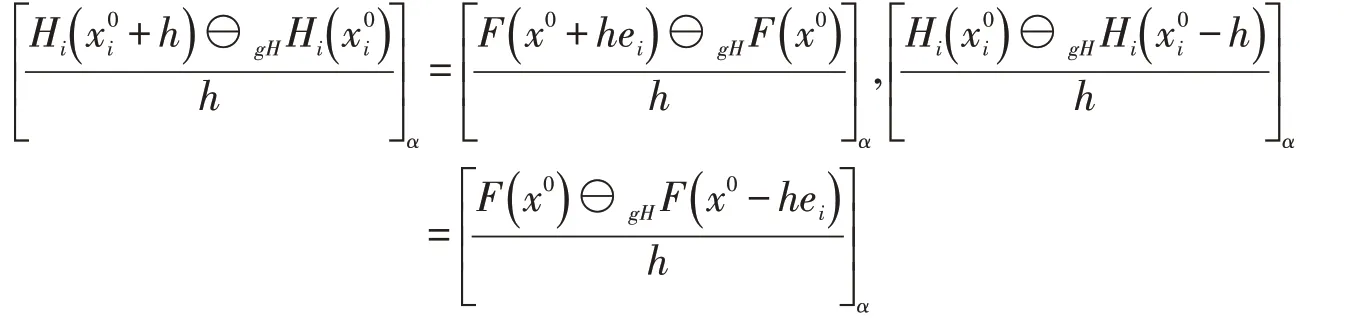
由F在x0处沿ei方向LgH-可微,则有
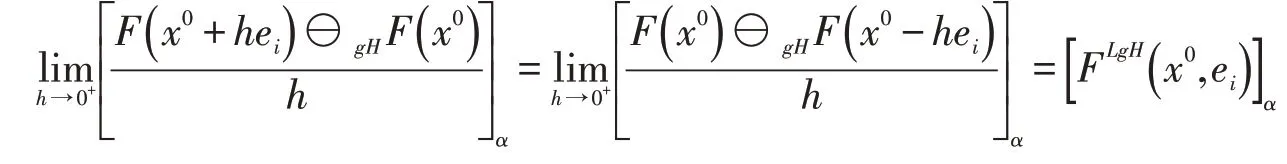
于是有
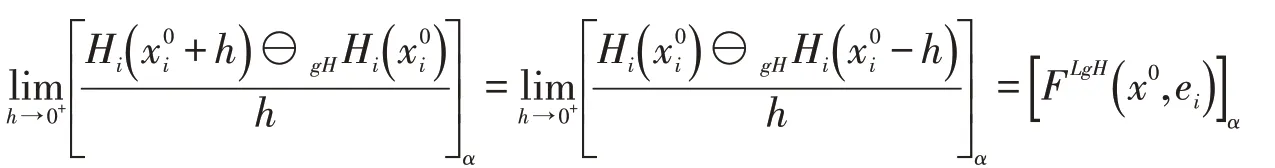
所以,根据定义2.2有F在x0处关于xi的LgH-偏导数存在,且
定义2.3设F:M→ℱ为模糊映射,.如果F在x0的邻域内关于xi的所有LgH-偏导数都存在且连续,则称F在x0处LgH-可微,且其LgH-梯度为
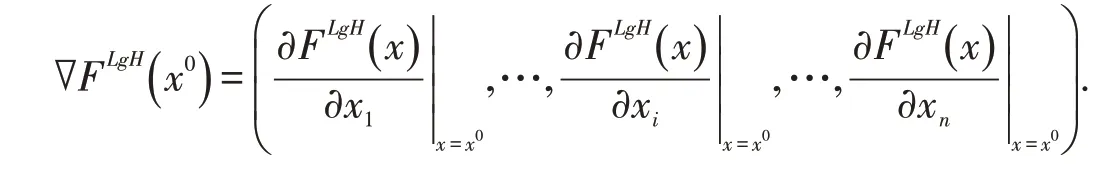
推论2.1设F:M→ℱ为模糊映射,.如果F在x0处LgH-可微,则
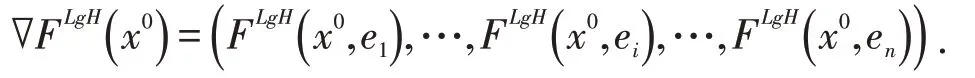
证明设F在x0处LgH-可微,则
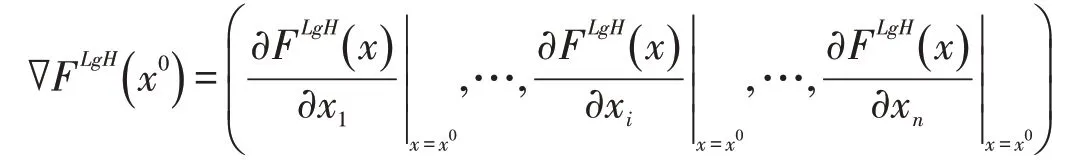
所以,根据定义2.3可得F在x0处的LgH-梯度可记为
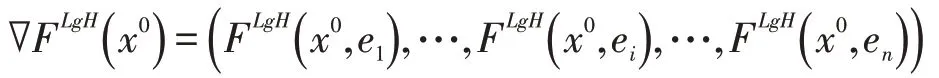
3 结论
模糊映射的可微性是模糊分析学的重要概念之一,对模糊优化问题及模糊微分方程的研究起着关键的作用.对模糊映射的LgH-方向可微性问题进行了研究,讨论了模糊映射的LgH-方向可微性与区间值映射的gH-方向可微性以及端点函数的方向可微性之间的关系,得到了模糊映射LgH-方向可微的几个必要条件.将在接下来的研究工作中继续讨论模糊映射的gH-可微性及其在模糊规划中的应用问题.

