应用于MEMS基频率源的CMOS温度传感器

黄继伟， 陈星, 王科平

(1. 福州大学物理与信息工程学院， 福建 福州 350108; 2. 天津大学微电子学院， 天津 300072)

0 引言

随着人类社会信息化、 网络化、 智能化进程， 越来越多的电子产品进入了人们的生产生活中, 而几乎所有的电子系统都需要基准频率源. 近年来基于MEMS( micro-electro-mechanical system)的频率源由于其体积小， 谐振频率高等原因， 成为替代石英晶体的一大热门研究[1-4]. 但是MEMS基的频率源本身温漂系数较大， 如BAW(bulk acoustic wave resonator )器件的温漂系数为5.00 × 10-4[1]， DETF(double-ended-tuning fork )器件的温漂系数也超过了4.80 × 10-4[2]， 截面Lame模式谐振器的温度系数达到了1.45 × 10-3[3]， 而目前研究最为热门的FBAR(film bulk acoustic resonator)器件未经温度补偿之前的温度系数甚至超过2.00 × 10-3[4]. 为使这些基于MEMS的频率源能在-55～125 ℃温度范围内提供稳定的基准频率， 就必须测量片上温度， 再根据温度信息进行相应的频率补偿， 实现较小的温漂.

传统温度传感器， 如热敏电阻、 铂电阻等因为体积大， 需要额外读取电路， 无法与CMOS工艺兼容实现片上集成， 并不适于当前需求. 而CMOS温度传感器则容易实现在片测温. 本研究以双极型晶体管(bipolar junction transistor， BJT)作为测温核心器件， 设计了一种测温范围为-55～125 ℃， 精度为± 0.5 ℃的片上CMOS温度传感器. 该温度传感器在片内集成了控制时钟电路， 只需输入一个基本时钟信号即可正常驱动， 大大降低了应用的复杂程度， 降低了与MEMS基频率源电路一起实现片上集成的难度.

1 BJT基温度传感器的基本原理

温度传感器的工作机制是将温度信号转换为数字信号输出， 因此需要获取与温度相关的信号， 通过ADC转换为数字信号， 并通过数学换算得到温度读数.

1.1 BJT基极-发射极电压与温度之间的关系

两个相同的PNP 晶体管QL和QR以1∶p的电流比率进行偏置， 如图1所示. QL的基极-发射极电压VBE1具有与绝对温度负相关的特性(complementary to absolute temperature， CTAT )， 该电压可以表示为：

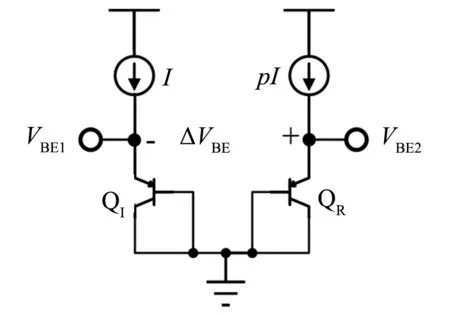
图1 双极型晶体管测温基本原理Fig.1 Basic operation of a BJT-basd temperature sensor

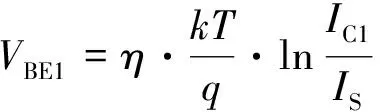
(1)

其中:η是一个与工艺参数相关的非理想因子(通常情况下，η≈1);k是玻尔兹曼常数(k=1.38×10-23);T是热力学绝对温度;q为电子电量;IC1是晶体管的集电极电流;IS则是晶体管的饱和电流.

类似地， 可得到QR的基极-发射极电压VBE2，VBE1和VBE2之间的差值为ΔVBE：

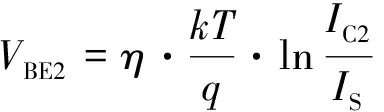
(2)

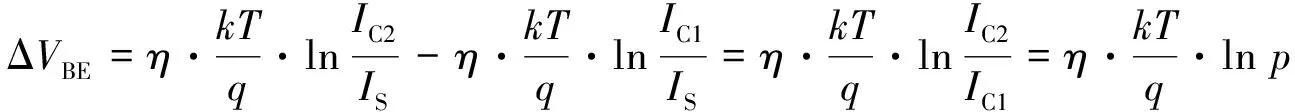
(3)

可以看出， 在电流密度比例p保持恒定的情况下， ΔVBE与绝对温度成正比例(proportional to absolute temperature， PTAT ).

1.2 温度传感器测温基本原理

由CTAT电压和PTAT电压线性组合， 可得到与温度无关的带隙基准电压：

VREF=Vbandgap=VBE+α·ΔVBE

(4)

其中:α是增益因子， 在晶体管的电流密度比例确定之后将保持不变. 通过模数转换器(analog-to-digital converter， ADC)可求出放大后的PTAT电压α·ΔVBE与基准电压VREF的比值μ：

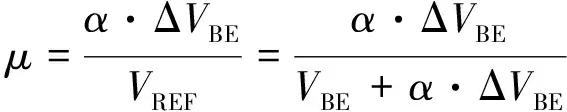
(5)

由于α·ΔVBE与绝对温度成正比例， 而基准电压VREF与温度无关， 因此比值μ将是与绝对温度成正比例的线性函数， 可以将该比值进行线性缩放， 得到摄氏温度读数DOUT：

DOUT=A·μ+B

(6)

其中:A和B均为常数， 通常情况下，A≈600，B≈-273.

设计产生与温度无关的带隙基准电压VREF需要设计精确的带隙基准电路， 而实际上与温度相关的两个量是VBE和ΔVBE， 对式(5)分子分母同时除以ΔVBE， 可得：

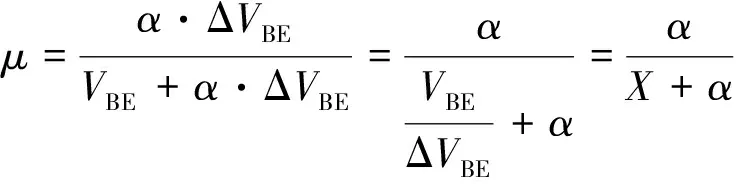
(7)

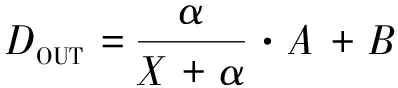
食用油是人们制作佳肴时的必备品。中粮集团旗下食用油品牌福临门已形成严格的可追溯体系，以确保油质安全。食用油的保质期一般为18个月，福临门产品每批次在出厂前都会留足18箱，作为每个月实时检验与追踪的样本，一旦发现问题，可根据每桶油的编码及追溯体系找到市场上留存的所有产品；反之，如果福临门产品在市场上被反馈有问题，也可根据编码查找到该产品的生产日期、生产线等一系列基础信息，以及市场中同一批次产品的流向。无论是正向追溯还是反向追溯，2小时内即可实现。

(8)

因此， 只需要求出式(7)中X=VBE/ΔVBE的值， 再通过式(8)进行数学换算即可得到摄氏温度[5].

2 温度传感器电路设计实现

根据前文所述， 可设计如图2所示的系统. 由图2可见， 测温前端电路产生与温度相关的电压VBE和ΔVBE， Zoom ADC则实现对二者比值X的量化并输出， 通过片外或者片内MCU则对X进行数学计算， 即可求得温度.

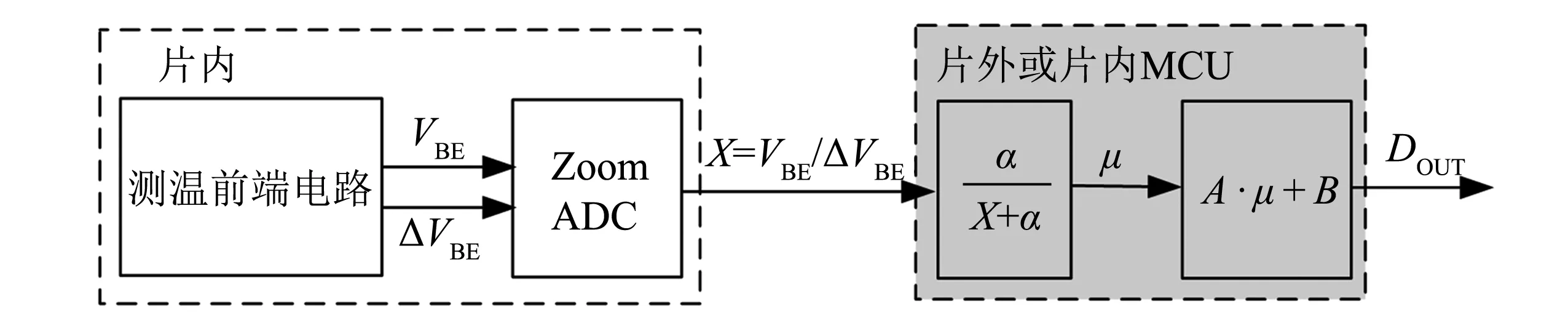
图2 温度传感器的系统框图Fig.2 Block diagram of the temperature sensor

2.1 测温前端电路

设计的测温前端电路如图3所示. 图中左侧为启动电路. 当电路处在不正常工作点时， 运放输出节点电位为高电位， PMOS电流源不导通. 此时，A、B点的电位为零， 使MN1截止，C点电位由MP1、 MP2提升到VDD， 使得MN2导通， 从而将运放输出节点的电位拉低， 共源共栅电流源导通. 当电路进入正常工作状态时，A、B点电位升高， 使MN1导通， 进而拉低C点电位使得MN2截止， 启动电路与偏置电路断开连接， 启动电路不再影响其他部分.

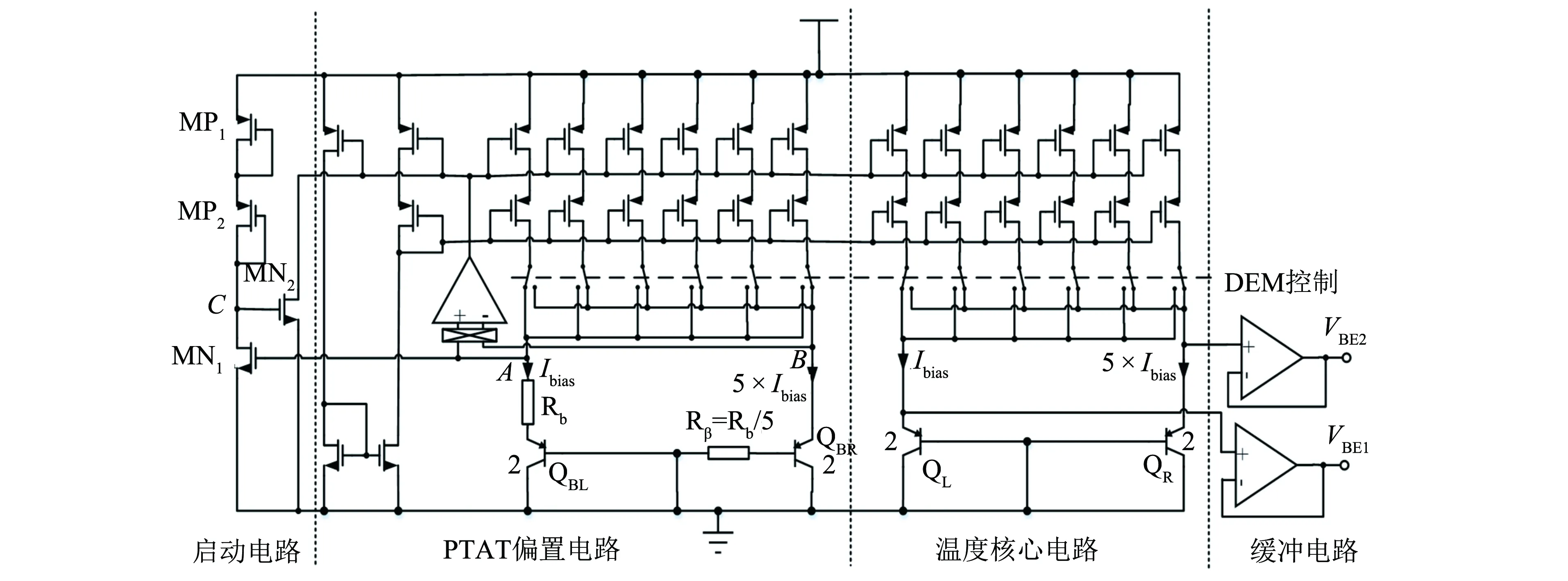
图3 测温前端电路Fig.3 Circuit diagram of the sensor front-end

实际上， BJT的VBE与温度之间并非完全一阶线性关系， 而是存在一定曲率. 通过使用PTAT偏置电流， 可以在一定程度上减弱曲率带来的影响[5]， 使VBE与温度关系更加准确， 适应大量程测温需求. 因此， 可通过偏置电路产生PTAT电流来偏置核心电路的晶体管. 通过运放的负反馈钳位， 图3中A、B节点的电位相等， 而通过两支路BJT的电流密度不同， 因此将以式(3)的方式产生电压差ΔVBE， 该电压差加在电阻Rb两端， 产生PTAT电流. 同时为了降低运放失调带来的影响， 使用了斩波运放.

伴随现代CMOS工艺的发展， 特征尺寸不断缩小， BJT的电流增益系数βF不断减小， 使集电极电流出现误差进而带来VBE的误差[6]. 在偏置电路中引入补偿电阻Rβ， 由于A、B节点的电位相等， 则可通过下式求得偏置电流：

将式(9)求得的偏置电流代入BJT的集电极、 发射极电流关系， 可得：

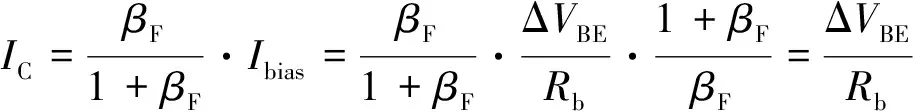
(10)

由式(10)可知， 集电极电流已经和电流增益系数βF无关， 从而从理论上消除了这个误差.

通过偏置电路产生的PTAT电流后， 通过电流镜复制到温度核心电路， 再通过动态匹配(dynamically element matched， DEM )电路来控制电流选择开关， 使6个镜像电流源的电流轮流单独偏置QL, 其余电流则偏置QR[7]. 即一个动态匹配周期内流过晶体管的平均电流为：

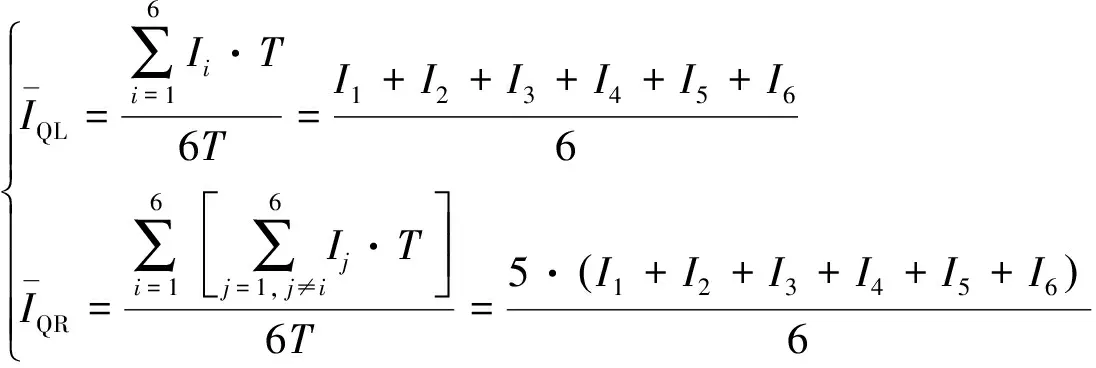
(11)

最后， 通过右侧的单位增益缓冲电路， 将温度核心电路所产生的VBE1和VBE2电压输出至后端电路， 不仅提高了对后端电路驱动能力， 也避免了对后端电路充放电导致的核心晶体管偏置电流发生变化， 进一步提高了系统的稳定性和精度.

2.2 缩放式模数转换器

设计的温度前端电路产生VBE1/ΔVBE的比值X在 -55～125 ℃范围内的取值为25.510至7.405， 可将该比值分为整数部分和小数部分， 即X=N+n， 其中整数部分N通过较为粗略的SAR阶段来量化， 小数部分n则通过较为精细的Sigma-Delta阶段来量化.

ADC在粗量化阶段， 通过SAR逻辑确定整数部分N， 如图4(a)所示, 细量化阶段如图4(b)所示. 以粗量化阶段得到结果作为细量化的基准， 将量化范围缩小至N和(N+ 1)之间， 从而可以使用Sigma-Delta ADC以更高的分辨率确定小数部分n. 通过粗量化阶段， 缩小了细量化阶段的量化范围， 降低了对Sigma-Delta ADC的分辨率的要求， 因此只需使用一阶Sigma-Delta电路.

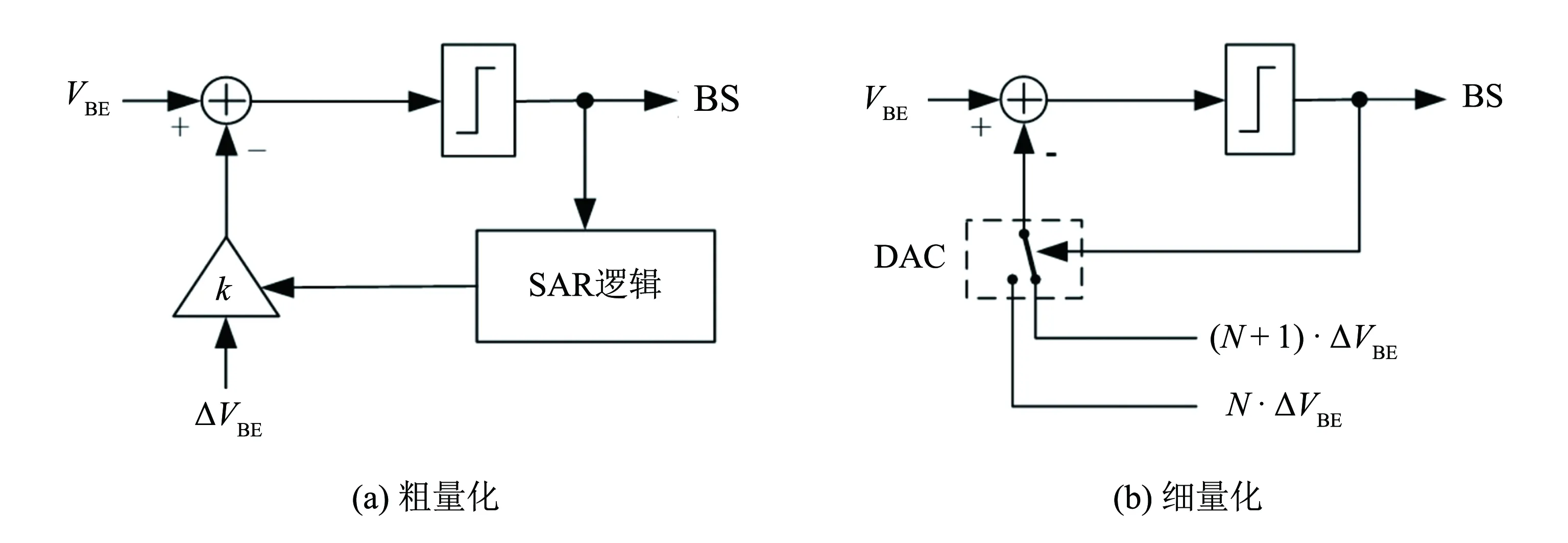
图4 缩放式ADC的量化过程示意图Fig.4 Block diagram of the quantification process of Zoom ADC

设计的缩放式ADC电路结构如图5所示， 整个ADC分为采样保持电路、 积分电路、 比较器和逻辑电路， 通过共用一个积分电路将SAR、 Sigma-Delta ADC两部分结合在一起， 降低了系统的复杂度和电路的功耗.

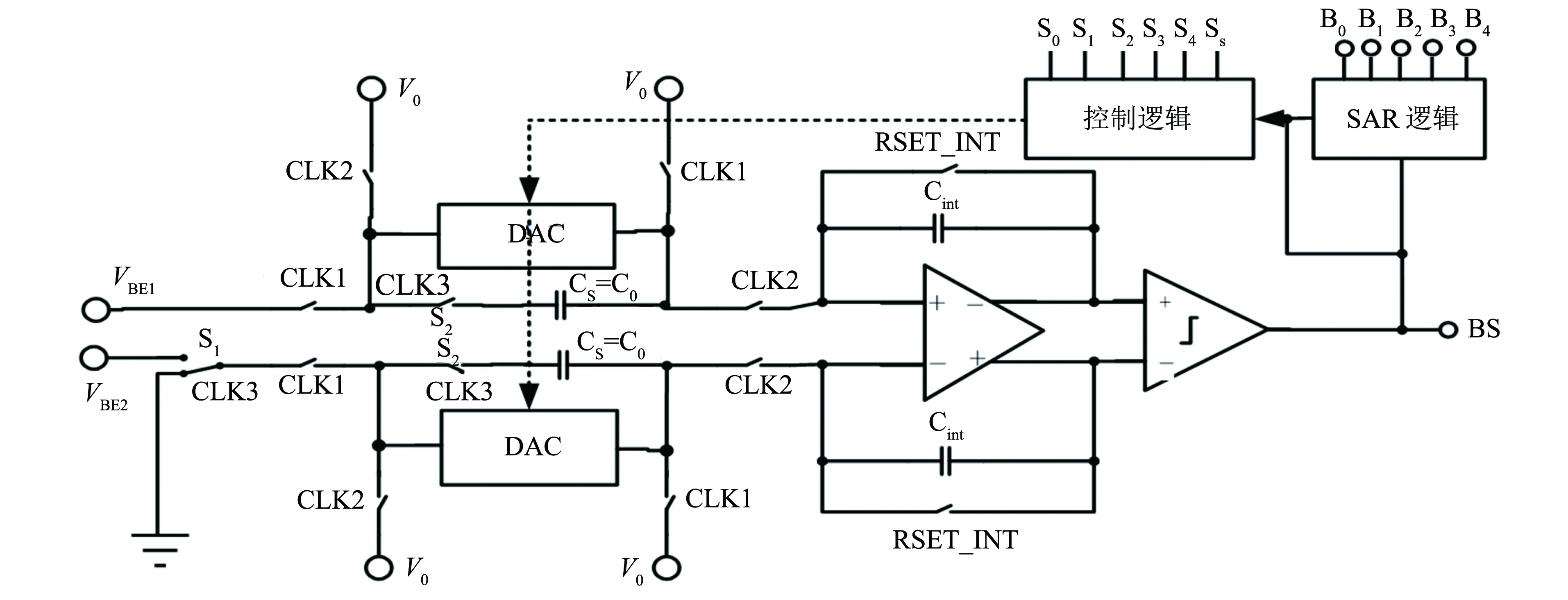
图5 ZOOM ADC的电路结构Fig.5 Circuit diagram of the ZOOM ADC

高温条件下， 开关的泄漏电荷会变得更严重. 特别考虑所采用的CMOS互补开关尺寸， 利用PMOS、 NMOS的泄漏正负电荷相互抵消以降低对积分电路的影响. 同时设计高灵敏度的比较器， 使其在低温下仍可以分辨很小的电压差以获取正确比较结果， 由此提高在高低温下的量化精度.

Zoom ADC在相关的控制时钟信号驱动下对输入信号进行量化. 如图6(a)所示， CLK1、 CLK2是一对非交叠时钟信号， 当CLK1=1, CLK2=0时， CLK1开关导通， CLK2开关断开， ADC 工作在采样模式， 采样电容CS(或电容阵列)对输入信号进行采样. 当CLK1=0, CLK2=1时， 电路工作在积分模式， CS(或电容阵列)上的电荷将转移至积分电容Cint上. 当CLK3=1时， 开关S1接到地， 此时的输入信号为VBE1， 开关S2接通， 通过采样电容CS进行采样和积分. 而当CLK3=0时， 开关S1接至输入端， 此时的输入信号为(VBE1-VBE2= -ΔVBE)， 开关S2断开， 电容阵列在逻辑控制电路下接入电路的电容值如下式所示， 并以这些电容对-ΔVBE进行采样积分， 在对两个信号进行积分采样后， 比较器将进行一次比较操作， 得到VBE1与k·ΔVBE的大小比较结果.

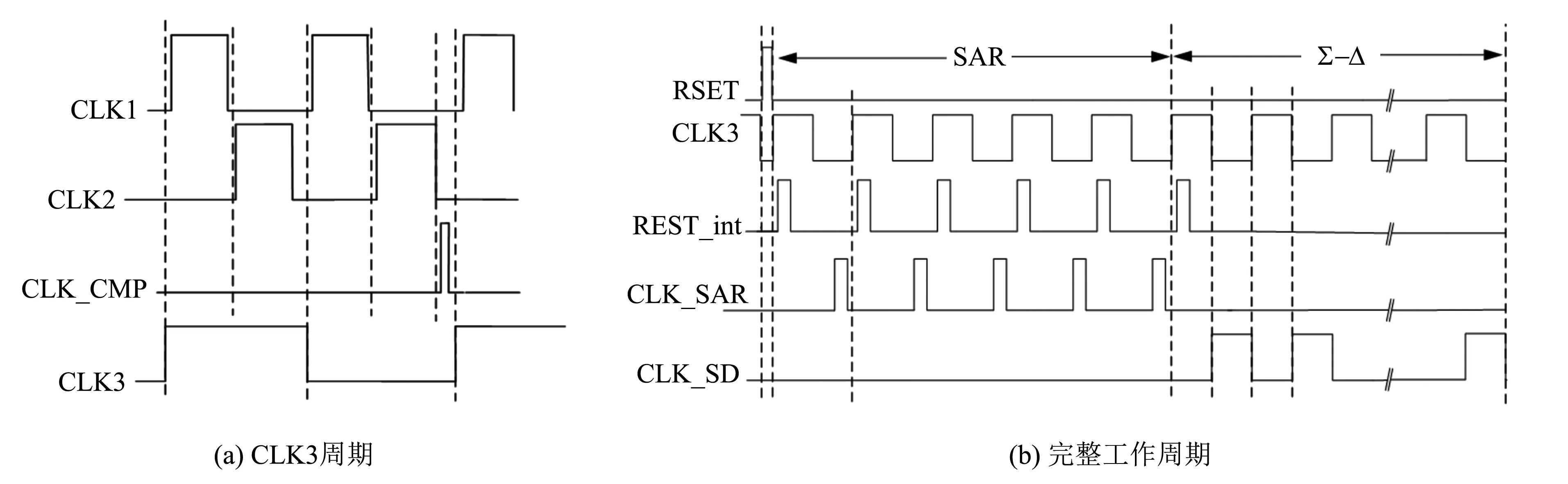
图6 缩放式ADC的时序图 Fig.6 Timing diagram of zoom ADC

(S4×24+S3×23+S2×22+S1×21+S0×20+SS)C0

(12)

ADC完整工作周期包括了SAR阶段和Σ-Δ阶段， 如图6(b)所示. 其中， SAR阶段为5个CLK3周期. 在每个CLK3周期开始时， 积分电容都要进行复位清零， 再开始采样和积分， 并在积分电路完成积分和比较后， CLK_SAR时钟将驱动SAR逻辑获取比较器的输出， 从而确定SAR逻辑的输出B4～B0. 此阶段CLK_SD保持为零， 令SS保持断开， 以公式(12)所示方式控制电容阵列中接入对应个数的采样电容. 在此后的256个CLK3周期则是Σ-Δ阶段. 仅在一开始对积分电容进行一次复位清零， 由于SAR逻辑不再变化， 因此S4-S0开关状态也将保持不变. 而开关SS将根据前一周期的比较结果BS变化， 对-ΔVBE采样的电容个数为N(BS=0)或N+1(BS=1)， 如果此阶段比较器的输出占空比为φ. 根据Σ-Δ基本原理， 有：

由公式(13)可知， 通过求得Σ-Δ阶段的比较器输出BS的占空比φ， 即可求得VBE与ΔVBE比值的小数部分. ADC的出量化值X为：

X=B4×24+B3×23+B2×22+B1×21+B0×20+φ

(14)

3 芯片版图设计与电路仿真结果

芯片的完整版图如图7所示， 总面积780 μm × 800 μm， 其中核心面积为380 μm × 480 μm， 小面积有利于与频率源等电路实现片上集成.

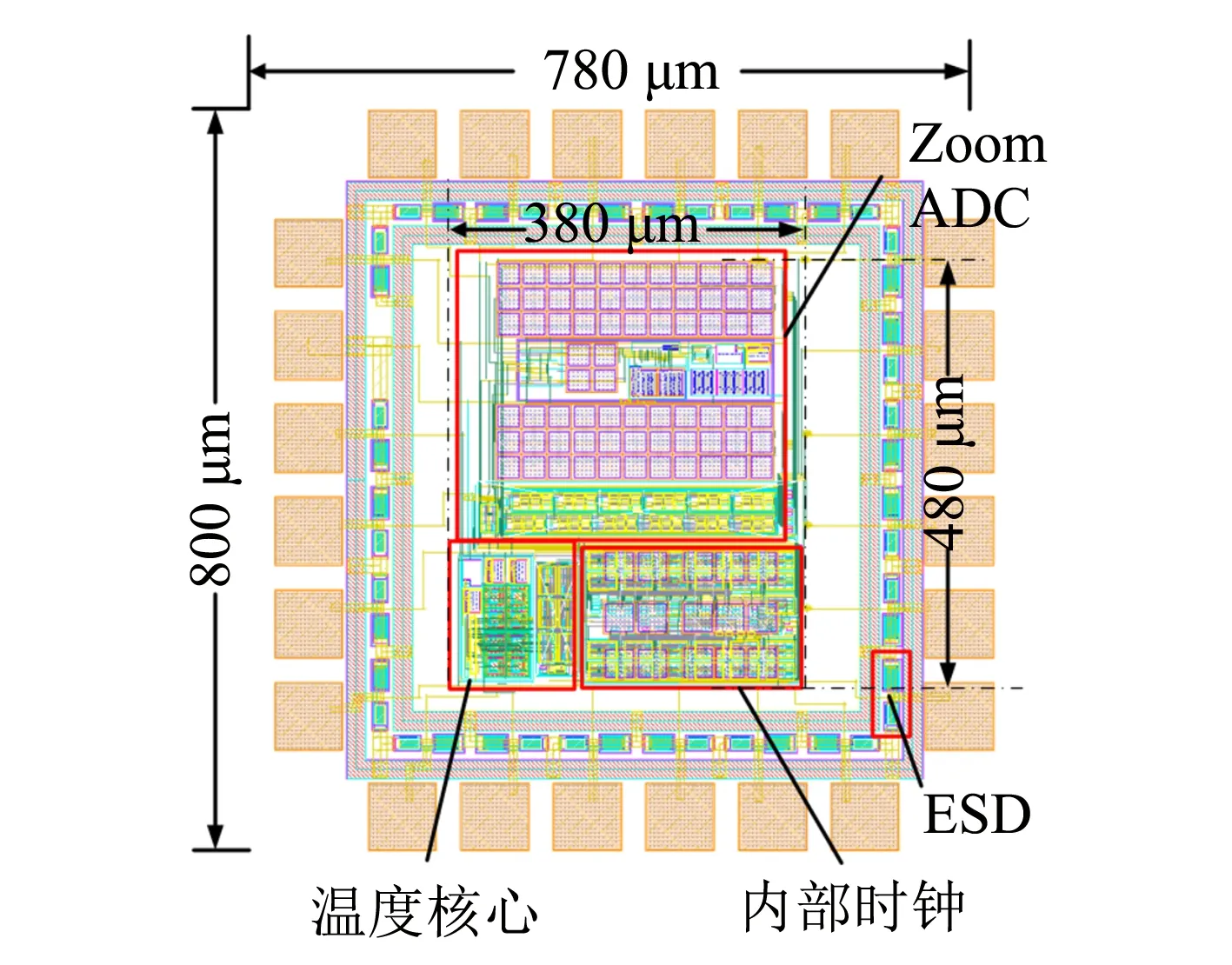
图7 电路版图Fig.7 Layout of the circuit

在不同温度点下对设计的温度传感器进行仿真， 根据式(14)计算得不同温度下的X值， 通过公式(7)计算得到相对应的μ， 并将在-55和125 ℃ 两个温度点获取的μ代入式(8)求得换算系数A、B， 再将A、B代入-55～125 ℃范围的其他温度点的数据计算， 得到读出tout和t误差如图8所示， 部分温度点下测量和计算的数据如表1所示， 而与部分BJT基CMOS温度传感器的性能对比如表2所示.

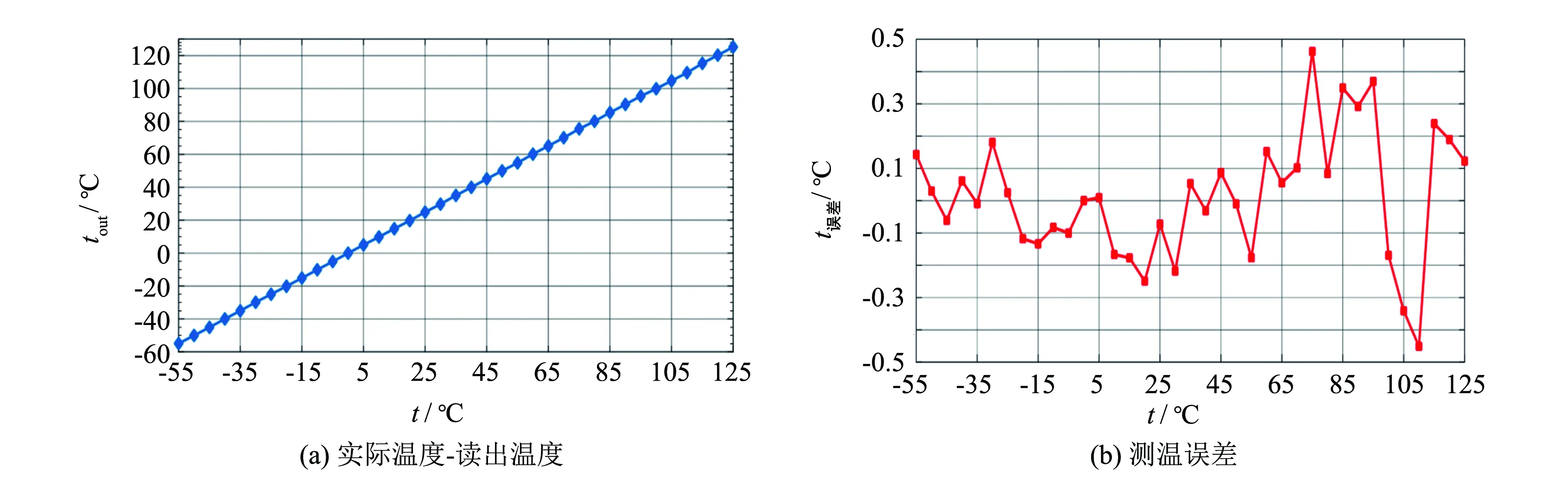
图8 测量结果 Fig.8 Measure results

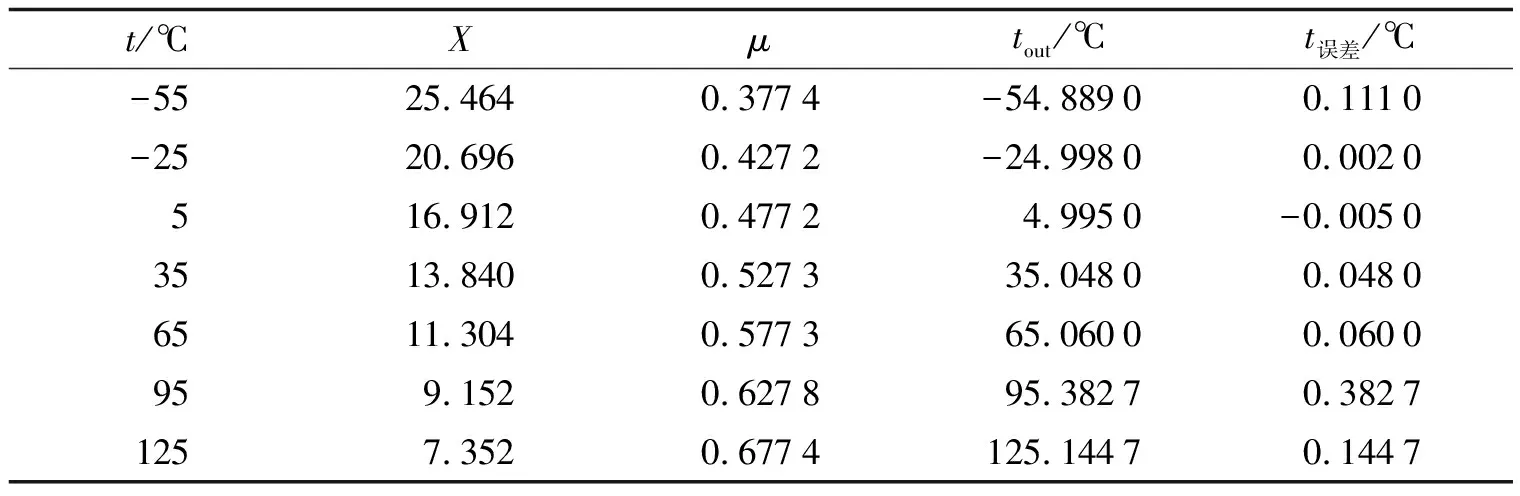
表1 不同温度点下的测温数据及误差

表2 CMOS温度传感器性能比较

4 结语

基于双极型晶体管的温度特性， 采用TSMC 0.18 μm CMOS工艺设计了一种BJT基的片上CMOS温度传感器. 仿真结果表明， 在1.8 V的电源电压下， 电路的平均功耗为240 μW， 在-55～125 ℃的测温范围内， 经两点拟合校正后的温度测量误差小于±0.5 ℃， 能够与频率源电路实现片上集成并提供较为精确的温度信号.