球形压头的滑动速度对材料微米划痕响应的影响
刘明, 严富文, 高诚辉
(福州大学机械工程及自动化学院, 福建 福州 350108)
0 引言
划痕测试法具有可靠性高、 操作简单、 样品易于制备等优点[1], 常被用于评估金属[2]、 聚合物[3-4]、 玻璃[5-6]、 涂层[7]等的各项力学性能, 比如: 断裂韧性[8]、 摩擦系数[9]、 划痕硬度[10]、 涂层和基体间的结合强度[11]等. 划痕测试的常用方法是给压头施加一定的法向载荷, 让其在试样表面划刻出一条沟槽, 进而测量试样的表面轮廓、 压入深度、 残余深度、 摩擦系数和声发射等参数[12]. 通常, 有许多因素会影响材料的划痕响应, 比如: 法向载荷[13]、 界面温度[14]、 表面粗糙度[15]、 试样倾斜[16-17]等. 此外, 滑动速度也是影响材料划痕响应的一个重要因素. Geng等[18]对PC进行纳米划痕实验, 发现滑动速度增大时, 压入深度和残余深度先线性减小, 然后几乎保持恒定; 弹性恢复率呈对数形式增加, 并可以通过Arruda-Boyce模型进行解释. Bandyopadhyay等[19]通过微米划痕测试研究了钠钙硅玻璃的变形行为, 发现压头和试样接触区域的最大拉应力和最大切应力均随滑动速度的增加而增大; 划痕宽度、 压入深度和磨损率均随滑动速度的增大而减小. Zhou等[20]在0.05~15 mm·s-1的速度范围内对紫铜进行划痕测试, 发现在较小的法向载荷下, 滑动速度对摩擦系数几乎无影响; 而当法向载荷较大时, 摩擦系数随滑动速度先减小随后趋于稳定.
微米划痕测试可模拟微切削和机械抛光过程, 其中, 滑动速度对最终的表面成型有着重要影响. PC、 熔融石英、 紫铜和镁合金AZ31四种材料在制造业中有着广泛应用。此外, 上述四种材料分别属于聚合物、 玻璃、 金属单质、 金属合金四种材料体系, 而这四种材料又是各自所属材料体系中非常典型的材料. 因此选择这四种材料作为研究对象, 每一种材料体系中均有一个代表性的测试结果, 可以对这四种材料体系的微米划痕测试中速度产生的影响形成全面的认识. 本研究使用球形压头对PC、 熔融石英、 紫铜和镁合金AZ31进行微米划痕测试, 分析了滑动速度对试样的压入深度、 残余深度、 弹性恢复率、 沟槽宽度和划痕摩擦系数的影响, 并计算划痕硬度以评估试样的抗划擦性.
1 微米划痕实验
在恒定的法向载荷下, 用Anton Paar MST2型微米划痕仪对PC、 熔融石英、 紫铜和镁合金AZ31进行划痕测试, 如图1(a)所示. 伴有堆积和凹陷形成时划痕沟槽横截面的示意图分别如图1(b)和(c)所示. 在室温和大气环境及干摩擦状态下进行实验, 测试过程中压头仅有法向位移, 样品进行水平移动. 微米划痕的测试过程分为三步: 首先, 压头在5 mN的法向载荷(该载荷非常小, 在样品表面产生的变形可忽略不计[9])下进行前扫描, 获得样品的初始表面形貌, 拟合出其最小二乘中线, 由此计算出PC、 熔融石英、 紫铜和镁合金AZ31的表面粗糙度Ra分别为: 0.010、 0.007、 0.025和0.038 μm; 其次, 在恒定的法向载荷Fn和滑动速度v下, 压头在样品表面上划刻出一条沟槽, 获得样品的侧向力Ft和声发射, 同时压头的垂直位移减去初始表面轮廓即为真实的压入深度dp, 划痕摩擦系数μ可通过μ=Ft/Fn计算得到[21]; 最后, 在5 mN的法向载荷下进行后扫描, 此过程中压头的垂直位移减去初始表面轮廓即为真实的残余深度dr. 相邻两次划痕测试间隔150 μm, 确保这两次测试之间不会相互影响. 对于PC、 紫铜和镁合金AZ31, 滑动速度范围为1~60 mm·min-1; 对于熔融石英, 为确保其划痕变量随滑动速度出现明显的变化趋势, 速度范围设置为0.1~60 mm·min-1. 当滑动速度v≤ 2 mm·min-1时, 划痕长度为1 mm, 采样频率随滑动速度而增加, 确保每次测试获得300个采样点; 当滑动速度v> 2 mm·min-1时, 每次划痕测试历时3 s完成, 划痕长度随着滑动速度而增加(例如, 当滑动速度为60 mm·min-1时, 划痕长度为3 mm), 采样频率为100 Hz, 同样确保每次测试获得300个采样点. 金刚石压头的半顶角ω=60°, 球形针尖的半径R≈100 μm, 压头的球锥转变深度dt=R(1-sinω)≈13.4 μm. 与试样相比, 刚性压头在划痕测试中的变形可忽略不计.

图1 微米划痕测试的示意图及堆积或凹陷形成时的沟槽横截面Fig.1 Schematic diagram of microscratch test and cross section of groove with the formation of pile-up or sink-in
2 微米划痕实验结果及分析
图2展示了Fn=0.75 N和v=17 mm·min-1时紫铜的3个划痕测试结果。这些划痕变量均处于波动状态, 是由样品不均匀的微观结构和塑性变形[22]、 粘滑行为[23]以及表面粗糙度等引起的. 此外, 紫铜和镁合金AZ31是多晶体, 其晶界和晶向会导致划痕变量发生波动; 对于PC, 其黏性阻力也可能导致划痕变量产生波动[24]. 残余深度和压入深度有几乎相同的变化趋势, 是因为在同一次划痕测试中沟槽各个位置的弹性恢复能力几乎相同. 在划刻的初始阶段和结束阶段测得的划痕变量不稳定, 相同的实验结果已被报导过[9, 22], 因此这两部分数据不参与计算; 在l/4~3l/4范围内的划痕变量处于稳定状态, 取该范围内测量数据的平均值作为各变量的最终取值, 以减小数据波动带来的误差. 此外, 在划痕测试中, 试样表面倾斜不可避免, 但倾斜角度非常小(约为0.16°), 对测试结果产生的影响可忽略不计.
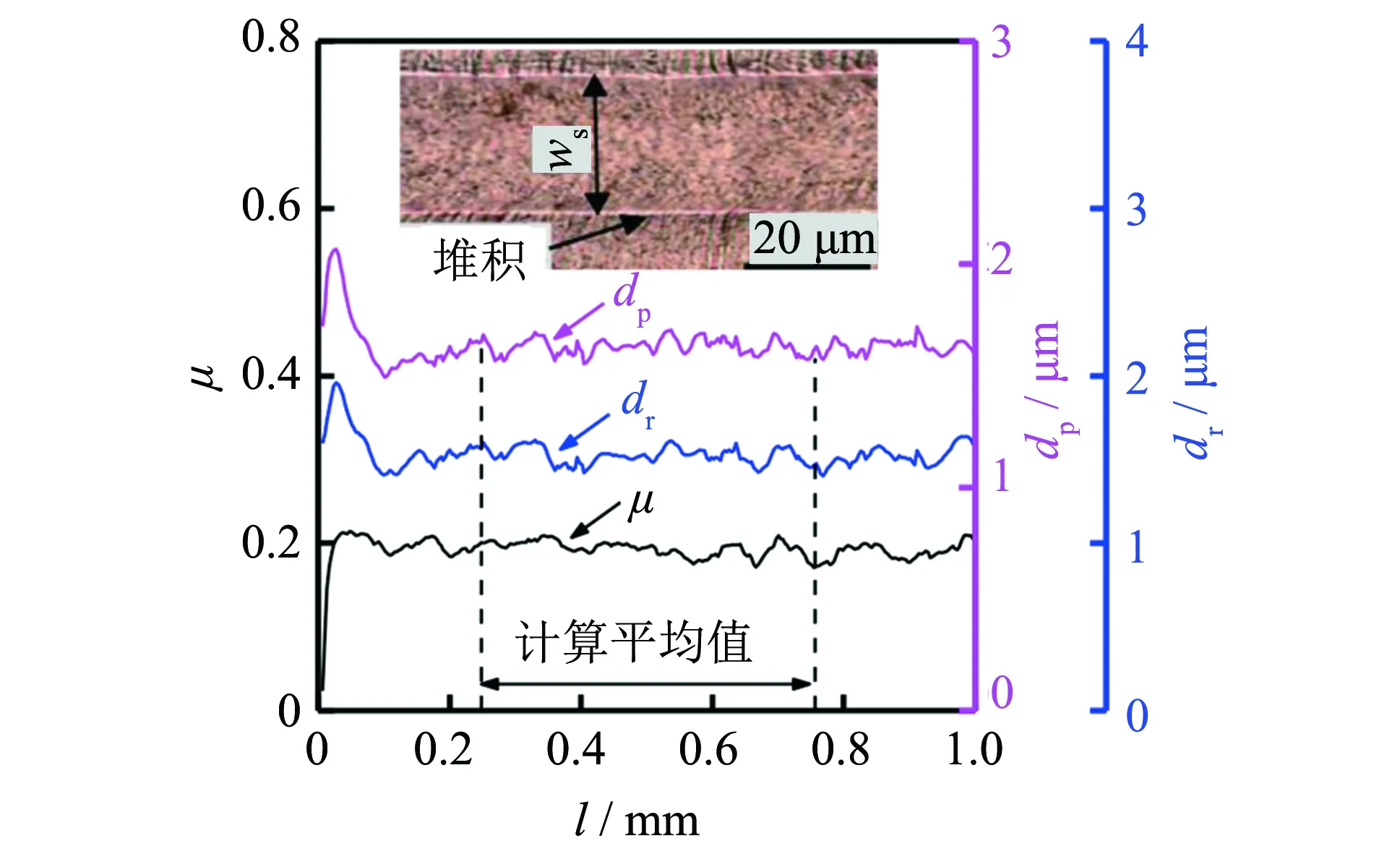
图2 紫铜的微米划痕测试结果及光学图像(Fn=0.75 N, v=17 mm·min-1) Fig.2 Results of microscratch test and optical image of copper(Fn=0.75 N, v=17 mm·min-1)
紫铜的微米划痕测试结果如图2所示, 其中插图为紫铜的划痕沟槽的光学图像. 划痕测试期间, 由于材料的塑性流动, 在其沟槽边缘形成堆积, 堆积的出现导致沟槽边缘不是完美的直线, Gao等[9]报导过相同的实验结果. PC和镁合金AZ31的划痕沟槽与紫铜的有相同的特征. 对不同的材料, 在不同法向载荷下, 滑动速度对材料微米划痕响应的影响可能存在差异[20], 但文中所用四种材料属于不同的材料体系, 各材料的测试结果间没有可比性. 对熔融石英进行划痕测试时, 取较小的法向载荷Fn=0.02 N, 是因为在更大的法向载荷下熔融石英易产生裂纹, 此时其划痕响应的变化趋势的机理变得更加复杂, 而本文着重研究无裂纹时试样的划痕响应; 若所取的法向载荷进一步减小, 实验仪器的精度不够. 划痕测试后熔融石英表面上的划痕沟槽在微米尺度下几乎无法被观察到. 在较大法向载荷下, Wei等[25]使用球形压头对熔融石英进行微米划痕实验, 发现其沟槽边缘上仍会发生凹陷, 因此, 根据微纳米划痕实验的测试结果, 可推测本实验中熔融石英的沟槽边缘会发生凹陷. 在文中所施加的法向载荷下, 所有样品在划痕测试后均未产生裂纹.
2.1 滑动速度对深度和弹性恢复率的影响
压入深度dp和残余深度dr与滑动速度v之间的关系分别如图3和图4所示, 可用幂函数进行拟合.

图3 压入深度与滑动速度之间的关系Fig.3 Variation of penetration depth with sliding velocity

图4 残余深度与滑动速度的关系Fig.4 Variation of residual depth with sliding velocity
在四种试样中, 紫铜的压入深度最大, 可达7.7 μm, 该深度远小于压头的球锥转变深度dt≈13.4 μm, 因此, 划痕测试中仅有压头顶端的圆球与样品接触. 压入深度和残余深度均随滑动速度的增大而非线性减小, 类似的实验结论已被报导过[26-27]. 随着滑动速度的增大, 样品发生硬化现象从而导致压入深度减小, 表明样品抵抗法向压入的能力不断增强. 在同一载荷下, 若用dp1(dr1)表示最大压入(残余)深度,dp2(dr2)表示最小压入(残余)深度, 那么PC、 熔融石英、 紫铜和镁合金AZ31压入深度的最大减小率(dp1-dp2)/dp1分别为10.4%、 39.7%、 20.2%、 10.6%. 残余深度始终小于压入深度, 是因为压头划刻之后划痕沟槽发生了弹性恢复. 上述四种材料残余深度的最大减小率(dr1-dr2)/dr1分别为81.7%、 70.6%、 29.9%、 19.3%, 和各材料对应的压入深度的减小率相比, 滑动速度对残余深度的影响更大.
压入深度代表总的变形量, 弹性恢复深度de=dp-dr代表弹性变形量, 因此, 弹性恢复率可定义为de/dp, 代表弹性变形在总的变形中所占的比例. 弹性恢复率与滑动速度之间的关系如图5所示, 幂函数的拟合结果与实验数据吻合. 随着滑动速度的增加, 弹性恢复率先迅速增大, 然后趋于平缓, 类似的实验结果已被报导过[18, 28]. PC是一种典型的聚合物, 会表现出黏弹性变形[29]. 因此, 在划刻过程中, 会展现出黏弹性恢复, 也就是其弹性响应有延迟, 划刻之后需要足够的时间以进行彻底的弹性恢复, 从而获得真实的残余深度[30]. 然而, 本实验中的残余深度是划刻之后立即测量的, 测试过程中并未考虑时间对残余深度的影响, 所测残余深度并非真实的残余深度, 但是PC的弹性恢复率在较大的滑动速度下几乎接近100%, 见图5(a), 意味着在足够大的滑动速度下, 由PC的黏弹性行为导致的延迟的弹性恢复很小, 其黏弹性对变形产生的影响大幅减弱, 可忽略不计, 弹性变形占主导[31]. 综上所述, 在PC的划痕测试中, 当滑动速度较小时, 黏弹性变形占主导; 当滑动速度较大时, 弹性变形占主导, 相同的结论已被报导过[24, 31]. 对于熔融石英,de/dp>50%, 见图5(b), 表明试样的弹性变形占主导, 对于硬脆材料, 这是合理的. 如图5(c)和(d)所示, 对于紫铜和镁合金AZ31这两种软金属,de/dp<50%, 表明试样的塑性变形占主导. 随着滑动速度的增加, 接触区域位错形成并不断积聚, 位错密度不断增大, 这会导致样品抵抗塑性变形的能力增强, 因此紫铜和镁合金AZ31的弹性恢复率不断增大. 弹性恢复率也可用于评估样品的抗划擦性[32], 其值随滑动速度而增大, 表明样品的抗划擦能力增强.

图5 弹性恢复率与滑动速度的关系Fig.5 Variation of elastic recovery rate with sliding velocity
2.2 滑动速度对划痕沟槽宽度的影响
忽略沟槽边缘的堆积与凹陷后压头与试样间的几何接触模型如图6所示. 接触区域在水平方向上的投影是一个弓形, 见图6(b), 水平方向上的接触投影面积Sh为:

图6 忽略堆积和凹陷的几何接触模型Fig.6 Geometrical contact model in which pile-up and sink-in are ignored
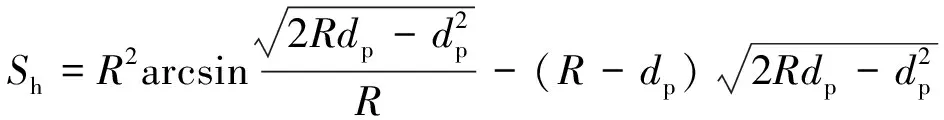
(1)
接触区域在垂直方向上的投影是一个半圆, 见图6(c), 垂直方向上的接触投影面积Sv为:

(2)
根据公式(1)和(2)计算的Sh和Sv存在一定的误差, 因为图6的模型中忽略堆积会导致计算的Sh和Sv偏小, 忽略凹陷会导致计算的Sh和Sv偏大.
在PC、 紫铜和镁合金AZ31的每一条划痕沟槽的光学图像中取5次测量值的平均值作为该条沟槽划痕宽度ws(见图2)的最终取值, 以减小堆积带来的测量误差. 在图6所示的几何接触模型中, 根据压入深度可计算几何接触宽度wc:

(3)
从划痕沟槽的光学图像中测量的划痕宽度ws、 根据图6所示的模型计算的几何接触宽度wc以及滑动速度v之间的关系如图7所示, 可用幂函数进行拟合. 图7(b)中没有划痕宽度ws, 是因为本实验中熔融石英表面的划痕沟槽几乎无法被观察到,ws无法被测量.ws和wc均随滑动速度的增大而非线性减小, Li等[33]报导过类似的实验结果.ws和wc主要受到压入深度的影响, 压入深度随滑动速度而减小, 从而导致二者减小. PC、 紫铜和镁合金AZ31的划痕宽度均大于几何接触宽度, 是因为沟槽边缘上存在堆积, 划痕宽度在堆积的最高点处进行测量, 而计算几何接触宽度时忽略了堆积, 所以划痕宽度所在的位置高于几何接触宽度所在的位置, 见图1(b). 随着滑动速度的增大, 划痕宽度和几何接触宽度之间的差值逐渐减小, 这是由于堆积高度随滑动速度而减小[34], 导致划痕宽度不断接近几何接触宽度. 如图7(a)所示, 在0.05 N的法向载荷下, PC的划痕宽度和几何接触宽度几乎重合, 是因为在较小的载荷下, 沟槽边缘形成的堆积不明显, 堆积对测量划痕宽度产生的影响非常小.

图7 划痕宽度和几何接触宽度与滑动速度的关系Fig.7 Variation of scratch width and geometric contact width with sliding velocity
2.3 滑动速度对划痕硬度的影响
划痕硬度被定义为单位面积上所承受的法向载荷, 根据图6所示的忽略堆积和凹陷后的几何接触模型, 由几何接触宽度wc可计算划痕硬度Hc[33]:

(4)
此外, 根据从划痕沟槽中测量的残余划痕宽度ws可计算划痕硬度Hs[35]:
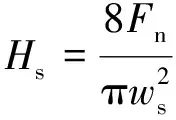
(5)
划痕硬度Hc或Hs与滑动速度v之间的关系如图8所示, 可用幂函数进行拟合. 随着滑动速度的增加, 划痕硬度先迅速增大, 然后趋于平缓, 与Zhu等[36]的实验结论相吻合. 在相同的法向载荷下, 由于PC、 紫铜和镁合金AZ31的wc

图8 划痕硬度与滑动速度的关系Fig.8 Variation of scratch hardness with sliding velocity
随着滑动速度的增大, PC的分子链段之间易于缠结并且缠结密度随之增加, 样品抵抗压头法向压入的能力增强, 从而导致其划痕硬度增加[24, 42]. 紫铜和镁合金AZ31塑性变形的机理是位错运动, 位错对二者的划痕硬度有重要影响. 位错密度随滑动速度而迅速增大, 导致位错缠结的形成, 这些位错优先在压头下边成核, 并阻碍连续运动位错的形成, 从而导致位错积聚[27]; 此外在晶界处位错也会受到阻碍, 也能导致位错的积聚, 进而出现应变率硬化现象, 导致二者的划痕硬度增加. 在另一方面, 根据公式(4)和(5), 在恒定的法向载荷下, 划痕硬度取决于沟槽的宽度, 宽度随滑动速度而减小(见图7), 导致划痕硬度增大. 划痕硬度可用来表征材料的抗划擦能力, 其值增大表明材料抵抗塑性变形和犁沟损伤的能力增强, 即抗划擦能力增强.
2.4 滑动速度对划痕摩擦系数的影响
当划痕测试中熔融石英和金属不产生裂纹时, 二者的侧向力Ft由黏着组分Fa和犁沟组分Fp组成[9, 25]. 相应地, 划痕摩擦系数μ由黏着摩擦系数μa和犁沟摩擦系数μp组成. 然而PC是一种典型的聚合物, 其黏弹性行为对摩擦响应有显著影响, 因此对于PC, 其划痕摩擦系数除了包含μa和μp外, 还包括黏弹性摩擦系数μv[24, 43]. 假设试样的侧向和法向硬度相等, 基于图6所示的几何接触模型, 可计算犁沟摩擦系数μp[9]:

(6)
如图9所示, 随着滑动速度的增加, PC的划痕摩擦系数μ先增加后减小, 与Zhang等[24]在较大法向载荷下报导的实验结果相吻合. 犁沟摩擦系数μp随着滑动速度而减小, 是因为压入深度减小导致犁沟效应减弱. 由于图6所示的几何接触模型中忽略了凹陷和堆积, 对垂直和水平方向的接触投影面积有一定影响, 进而影响μp. PC的黏着摩擦系数μa[43]可根据下式计算:

图9 PC的摩擦系数与滑动速度的关系Fig.9 Variation of friction coefficient of PC with sliding velocity

(7)
式中:τ表示界面剪切应力;p是接触区域的局部压力, 也即样品的划痕硬度.τ和p之间的关系[43]可用下式表示:
τ=τ0+αp
(8)
式中:τ0和α是对τ和p间的关系进行线性拟合时的拟合参数.黏着摩擦系数μa[43]可表示为:

(9)
随着滑动速度增大, 划痕硬度增加, 导致μa减小, 在聚合物的划痕测试中报导过类似的实验结果[44]. 除PC外, 大量聚合物的τ0和α值被给出[45], 因此, 需要进一步的研究以确定PC的τ0和α值, 从而计算其μa.
图9(c)表明当滑动速度在1~12 mm·min-1的范围内时, PC的μa+μv随滑动速度而增大, 由于μa随滑动速度而减小, 因此μa+μv的增加归因于μv的增大. 随着滑动速度的增加, 在应力活化和温升的作用下, 压头和PC的接触区域的分子链段开始运动并且在该区域变得杂乱无章[46-47]. 在这种情况下, 分子链段间的缠结和剪切作用加剧, 内部能量耗散增加, 造成PC的黏性阻力随着滑动速度而增大, 从而导致μv增加[24]. 但在较高的滑动速度下, 由于压头和样品间接触时间减少, 接触区域的分子链段无法跟上压头的运动, 从而导致黏性阻力减弱,μv减小[24]. 因此, 当滑动速度大于12 mm·min-1时, 在μa、μp和μv均减小的情况下, PC的划痕摩擦系数μ减小.
熔融石英和金属的黏着摩擦系数μa和黏着切应力pa[9]可由下式计算:

(10)
如图10所示, 熔融石英的划痕摩擦系数μ、 黏着摩擦系数μa和黏着切应力pa均随滑动速度的增加而先增大后减小, 最后趋于稳定. 因为压入深度减小导致犁沟摩擦系数μp始终减小, 所以可认为黏着摩擦系数的变化决定了划痕摩擦系数的变化趋势. 犁沟摩擦系数的值较小, 是因为施加的法向载荷较小, 导致压入深度较小, 划痕沟槽几乎无法被观察到, 犁沟效应不显著. 犁沟摩擦系数远小于黏着摩擦系数, 表明划痕测试中黏着摩擦占主导. 在较小的滑动速度下, 压头后边的拉应力随着滑动速度而增大, 从而导致划痕摩擦系数μ增加[48]. 当滑动速度大于20 mm·min-1时, 压头和样品间的摩擦状态符合动摩擦定律,μ的变化趋势满足Amonton定律[49], 所以其值几乎保持不变, 约为0.104.

图10 熔融石英的摩擦系数和黏着切应力与滑动速度的关系Fig.10 Variation of friction coefficient and adhesion shear stress of fused silica with sliding velocity
如图11所示, 紫铜的划痕摩擦系数μ、 黏着摩擦系数μa和黏着切应力pa均随滑动速度的增加而先增大后减小. 根据公式(8), 在恒定的法向载荷Fn下, 即使垂直接触投影面积Sv随着压入深度的减小而减小, 在较小的滑动速度下, 接触区域样品的应变硬化可能导致pa增大, 进而导致μa增大; 在较高的滑动速度下, 接触区域的局部热软化可能导致pa减小[10], 在Sv也减小的情况下, 导致μa减小. 由于压入深度减小导致犁沟摩擦系数μp始终减小, 因此划痕摩擦系数μ的变化趋势主要归因于黏着摩擦系数μa的变化. 在较小的法向载荷0.75 N下,μ随滑动速度没有显著的变化, 其值可视为一个常数, 约为0.199. 此外, 在相同的法向载荷下,μa>μp, 表明在划痕测试中紫铜的黏着摩擦占主导, 所以可通过划刻紫铜的方法来清洁压头.

图11 紫铜的摩擦系数和黏着切应力与滑动速度的关系Fig.11 Variation of friction coefficient and adhesion shear stress of copper with sliding velocity
如图12所示, 对于镁合金AZ31, 随着滑动速度的增大, 划痕摩擦系数μ、 黏着摩擦系数μa和黏着切应力pa先减小后增大. 压入深度减小导致犁沟摩擦系数μp始终减小, 因此划痕摩擦系数μ的变化趋势主要取决于黏着摩擦系数μa的变化.

图12 镁合金AZ31的摩擦系数和黏着切应力与滑动速度的关系Fig.12 Variation of friction coefficient and adhesion shear stress of magnesium alloy AZ31 with sliding velocity
根据公式(8), 在恒定的法向载荷Fn下, 由于压入深度减小, 垂直接触投影面积Sv始终减小时,μa的变化趋势主要取决于pa. 但是还需要进一步的实验以研究pa随滑动速度的变化趋势的机理进而解释滑动速度对μ的影响. 镁合金AZ31的划痕摩擦系数随滑动速度的变化趋势与其它材料的并不一样, 表明不同材料的划痕摩擦系数对滑动速度的敏感性不同, 滑动速度对各材料的划痕摩擦系数的影响比较复杂.
3 结语
使用球形压头研究其滑动速度对PC、 熔融石英、 紫铜和镁合金AZ31的微米划痕响应的影响, 主要结论如下:
1) 随着滑动速度的增加, 压入深度、 残余深度和划痕沟槽的宽度均非线性减小. PC、 熔融石英、 紫铜和镁合金AZ31压入深度的最大减小率分别为10.4%、 39.7%、 20.2%、 10.6%, 残余深度的最大减小率分别为81.7%、 70.6%、 29.9%、 19.3%. 与压入深度的减小率相比, 滑动速度对残余深度的影响更大. 对于PC、 紫铜和镁合金AZ31, 由于堆积的形成, 从划痕沟槽的光学图像中测量的划痕宽度大于由几何接触模型计算的几何接触宽度.
2) 随着滑动速度的增大, 弹性恢复率和划痕硬度先迅速增大, 随后趋于平缓; 材料的抗划擦能力随二者的增大而增强. 所测材料的最大划痕硬度均小于其纳米压痕硬度. 划痕测试中, PC的主要变形机制为黏弹性和弹性变形; 熔融石英的主要变形机制为弹性变形; 紫铜和镁合金AZ31的主要变形机制为塑性变形.
3) 随着滑动速度的增大, PC和紫铜的划痕摩擦系数均先增大后减小, PC的摩擦响应与其黏弹性行为密切相关. 熔融石英的划痕摩擦系数先增加后减小, 最后趋于一个常数, 约为0.104. 镁合金AZ31的划痕摩擦系数先减小后增大. 不同材料的划痕摩擦系数随滑动速度的变化趋势不同, 表明滑动速度对各材料的划痕摩擦系数的影响比较复杂. 四种材料的犁沟摩擦系数均非线性减小. 熔融石英、 紫铜和镁合金AZ31的划痕摩擦系数的变化趋势主要取决于黏着摩擦系数的变化.

