基于Abaqus/Python 的梳理纤维网三维建模

陈小明 ，李晨阳 ，谢军波 ，张一帆 ，李 皎 ，陈 利

（1.天津工业大学 纺织科学与工程学院，天津 300387；2.天津工业大学 先进纺织复合材料教育部重点实验室，天津300387；3.天津工业大学机械工程学院，天津 300387）

梳理纤维网[1-2]的数字化建模是进行三维针刺[3-4]成型数值模拟的关键基础，国内外关于数字化生成非重叠随机纤维网已有较多研究，包括Random Sequential Adsorption（RSA）方法[5-9]、改进 RSA[10]、沉积方法[11-13]、Monte Carlo 方法[14-16]、force biased 方法[17-18]、图像重构[19]等。然而这些方法主要用于短纤维和小长径比（≤50）纤维网建模，关于具有大长径比特征的梳理纤维网三维重构的研究报道很少。

本文提出基于Abaqus/Python 的梳理纤维网三维建模方法，包括纤维模型构建、纤维分层生长和纤维整体物理沉积3 方面内容。

1 建模思路

梳理纤维网如图1 所示。

图1 梳理纤维网Fig.1 Carded fiber web

由图1 可知，纤维网在经过梳理之后，网内纤维的形态特征主要呈现出大弯曲纤维和准直线纤维2种状态，且纤维近似面内取向。因此，本文提出针对上述2 种模型叠加梳理纤维网的建模思路，并基于Abaqus/Python 软件平台进行梳理纤维网建模。

基于Abaqus/Python 平台的建模过程分为4 步：

（1）在初始平面内，基于准直线纤维、大弯曲纤维杆单元链模型，自由生长生成纤维；

（2）纤维通过移动、旋转定位至空间非重叠平面上，构建空间纤维网；

（3）对纤维的有限元网格进行自动划分，并且完成对纤维材料属性的赋予；

（4）所有纤维在重力作用下，实现一次性沉积成型，构建梳理纤维网三维模型。

2 纤维模型构建

本研究中的梳理纤维网建模主要包含大弯曲纤维和准直线纤维这2 种纤维类型。本文通过将纤维全部作为面内的纤维来简化纤维模型。

2.1 准直线纤维模型

用首尾相连的杆将准直线纤维进行连接，形成杆链结构，根据自由生长算法在初始平面内生成纤维，模型如图2 所示。

图2 准直线纤维模型Fig.2 Quasi-linear fiber model

准直线纤维的自由生长算法如下：

（1）定义初始生长点P0（0，0）。

（2）定义纤维总长度L、生长方向角度增量θn、纤维杆单元长度Ln。其中，L 取值范围根据梳理纤维网统计获得；生长方向角度增量θn通过纤维的弯曲程度来决定；纤维杆单元长度Ln可以根据建模精度来确定。

（3）计算出单根纤维中含有多少根杆单元以及所含杆单元的端点坐标Pn（Xn，Yn）。

（4）基于各杆单元坐标Pn（Xn，Yn），通过调用Abaqus的直线命令（s.Line（…））生成准直线纤维。

（5）准直线纤维的总长SUM_QL 不断累加，SUM_QL=SUM_QL+L。

2.2 大弯曲纤维模型

大弯曲纤维模型如图3 所示。

图3 大弯曲纤维模型Fig.3 Large bending fiber model

通过控制点A、B、C 定义大弯曲纤维的样条曲线模型。第K 条大弯曲纤维可以用参数组Uk（XA，YA，XB，YB，XC，YC）来定义，其中点 A、点 B 和点 C 的坐标分别定义为 A（XA，YA）、B（XB，YB）和 C（XC，YC）。

大弯曲纤维的自由生长算法如下：

（1）定义初始生长点 A（0，0）。

（2）定义纤维总长度L、生长方向角度增量θn、纤维杆单元长度L1和L2。L 取值范围根据梳理纤维网统计获得；且L1和L2的长度之和约等于总长度L；增量角度θ1、θ2的取值范围由纤维弯曲的程度来决定。

（3）计算控制点 B（XB，YB）、C（XC，YC）的坐标。

（4）根据控制点 A（XA，YA）、B（XB，YB）、C（XC，YC），调用Abaqus 样条曲线绘制命令（s.Spline（…））生成大弯曲纤维。

（5）大弯曲纤维的长度SUM_SC 不断累加，SUM_SC=SUM_SC+L。

当出现建模区域内纤维的总长SUM 大于SUM_QL 与SUM_SC 的总长时，程序就会继续生成新的纤维，反之则终止纤维模型搭建。

3 空间纤维网构建

3.1 构建算法

纤维空间位置模型的构建如图4 所示，将初始平面上生成的纤维转移到了空间的特定位置。

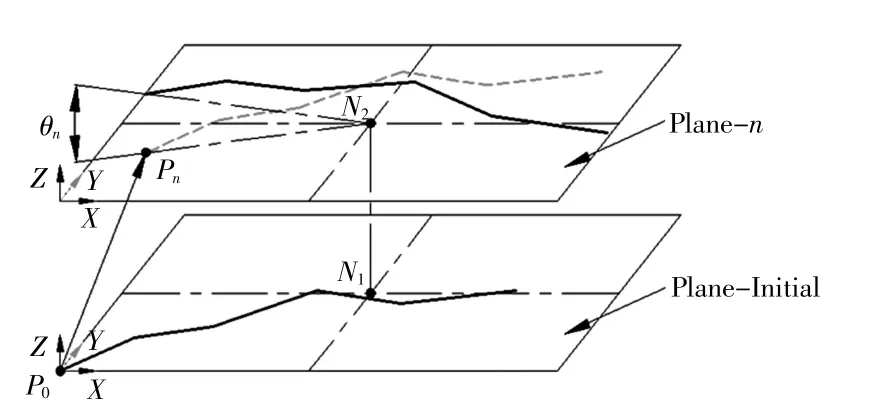
图4 纤维空间位置构建模型Fig.4 Construction model of fiber spatial position

由图4 可知，在厚度方向（Z 方向）上定义了一系列的彼此相互平行的平面，相邻平面的间距设为纤维直径，如此避免了纤维之间产生交叉重叠。纤维在初始平面内（Plane-Initial）生成，并移动至特定平面（Plane-n），进一步随机旋转一定的角度，完成分层自由生长，为后续沉积奠定基础。纤维空间位置的构建算法如下：

（1）建立初始平面和空间系列平面，其中平面间距值为纤维直径（d）大小；

（2）基于2.1 的纤维自由生长算法，在初始平面中生成纤维i；

（3）定义纤维i 在X、Y 和Z 方向上的随机位移量ΔXi、ΔYi和 ΔZi，其中 ΔZi=i × d（i≥0），ΔXi和 ΔYi需要根据纤维长度最大值 Lmax来决定，0≤ΔXi≤2 × Lmax，0≤ΔYi≤2 × Lmax；

（4）调用 Abaqus 的纤维移动命令（a.translate（…）），纤维从 P0点移动至 Pi点；

（5）沿轴线N1N2随机产生纤维i 的旋转角度Δθi；

（6）执行 Abaqus 的旋转命令（a.rotate（…））实现纤维旋转 Δθi；

（7）执行 i=i+1 循环，循环（3）到（6），直到产生n 根纤维。

3.2 算法验证

基于Abaqus 和Python 语言，对准直线纤维、大弯曲纤维的自由生长算法，以及纤维分层自由生长算法进行验证（包括单一和混杂纤维），具体的输入参数如表1 所示。梳理纤维网面密度为18.3 g/m2，厚度值为0.35 mm，纤维取向和长度取值根据图1 所示的实际梳理纤维网经实验测量得到，纤维的取向分布及长度分布如图5 和图6 所示。

图6 纤维长度分布图Fig.6 Distribution of fibers length

表1 生成纤维网的输入参数Tab.1 Input parameters of generated fiber web

图5 纤维方向分布图Fig.5 Distribution of fibers orientation

基于输入参数计算生成纤维网模型，单种纤维分层自由生长和多种混杂纤维分层自由生长的纤维网模型分别如图7、图8 所示。

图7 单一纤维分层生长的纤维网模型Fig.7 Single fiber web model for layered growth

图8 多种混杂纤维分层自由生长的纤维网模型Fig.8 Various hybrid fibers web model for layered free growth

由图7、图8 可知，本文提出的准直线纤维、大弯曲纤维的自由生长算法以及纤维分层自由生长算法可行，该算法可以实现单一和混杂纤维的分层生长。

4 纤维网一次性沉积成型

由于纤维网所含纤维数量众多，人工操作软件并且进行逐根建模存在很大难度，本研究采用Python 语言自动赋予材料属性和网格自动划分的计算脚本程序，通过Abaqus 软件平台运行该程序。其中，纤维自动网格划分需要设置梁单元的类型和大小，赋予材料属性过程中需要定义参数包括弹性模量、密度、梁横截面半径等。

纤维在沉积之前进行自动化网格划分和材料属性赋予，如图9 所示，所有纤维都被划分成不同数目的梁单元，按照计算的精度要求合理选取梁单元的长短，梁单元被划分的越小，计算的精度就越高，但同时计算消耗也会相应增加。纤维网格的自动划分和材料属性的自动赋予为一次性整体物理沉积奠定了基础。

图9 纤维在沉积之前进行自动化网格划分Fig.9 Automated meshing of fibers prior to deposition

以3.1 节生成的纤维网模型进行一次性物理沉积，模型中的纤维网尺寸为240 mm×240 mm×77.4 mm，如图10 所示。所有纤维整体沉积的有限元模型，压板和沉积底板的外形尺寸都为240 mm ×240 mm，加压板可以有效控制沉积纤维网的厚度。压板采用C3D8R单元，单元数462；沉积底板单元为四节点曲面壳单元S4R，单元数100；纤维选取两节点空间线性梁单元B31，梁单元数量为14 545。

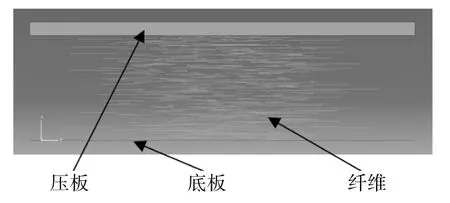
图10 纤维沉积有限元模型Fig.10 Finite element model of fiber deposition

沉积有限元模型中的接触较为复杂，包括压板、纤维和底板间的接触，采用通用法向硬接触，切向摩擦因数值采用0.3，沉积数值模拟的参数设置如表2所示。沉积底板固定不动，压板采用位移边界条件，设置下降位移为77.05 mm，沉积后形成梳理纤维网。

表2 沉积数值模拟的参数设置Tab.2 Parameters for deposition numerical simulation

纤维一次性沉积过程如图11 所示，在重力作用下，纤维和压板向下运动，经过初始沉积过程和压板压实过程，最终得到沉积完成的梳理纤维网和代表体积单元（RVE）。

图11 纤维一次性沉积过程Fig.11 Fiber disposable deposition process

纤维整体一次性沉积后的纤维网厚度为0.35 mm，体积分数为2.37%，与图1 中的梳理纤维网参数一致；通过DHU-11 纤维取向仪对纤维的取向进行测试，沉积的纤维取向结果和分布对比如图12 和图13 所示。

由图12 和图13 可知，沉积的梳理纤维网中纤维的取向主要分布在75°~105°区间，整体趋势表现为正态分布，与图1 所示的实际梳理纤维网统计结果一致。

图12 基于DHU-11 的沉积纤维取向测试结果Fig.12 Test result of deposition fiber orientation by DHU-11 fiber orientation analyzer

图13 纤维取向分布对比Fig.13 Comparison of fiber orientation distribution

5 结 论

（1）本文提出了基于Abaqus/Python 的梳理纤维网三维建模方法，即纤维分层生长和纤维一次性整体沉积方法，实现了梳理纤维网建模，可构建大长径比梳理纤维网数字化模型。该方法不仅适用于单种纤维，也可以实现多种杂化纤维梳理纤维网的三维建模。

（2）有限元模型中采用压板，可通过控制压板的位移边界条件，实现梳理纤维网厚度的有效控制。在本文实验条件下，纤维整体一次性沉积后的纤维网厚度为0.35 mm，体积分数为2.37%，纤维的取向主要分布在75°~105°区间，整体趋势表现为正态分布，与实际梳理纤维网统计结果一致，说明建模结果准确可行。

（3）沉积模拟生成的梳理纤维网可用于裁剪代表体积单元，后续将在三维针刺成型数值模拟及其复合材料性能有限元分析中开展进一步的研究。