PMMA 涂层玻纤织物固化过程中溶剂的扩散机制

郑振荣 ，毕月姣 ，王佳为

（1.天津工业大学 纺织科学与工程学院，天津 300387；2.天津工业大学 先进纺织复合材料教育部重点实验室，天津300387）

涂层织物是指通过在织物基材上涂覆聚合物或其他材料，形成的织物与聚合物的复合织物。常用的高聚物溶液种类很多，如有机硅树脂、丙烯酸树脂和聚氨酯等，其中丙烯酸树脂的薄膜透明、不易泛黄，具有良好的化学稳定性、耐候性和阻燃性，对玻璃纤维具有较好的粘合力，且价格低廉，因此在建筑、装饰、交通及军事领域得到了广泛应用[1-4]。在涂层织物固化过程中，干燥是关键的工艺步骤，溶剂扩散是控制干燥速率的关键因素，不仅决定了薄膜中残留溶剂的含量，还影响了薄膜的性能[5]。

目前国内外学者在建立涂层材料溶剂扩散过程的数值模型方面做了许多有益的尝试。如Arya[6]将聚甲基丙烯酸甲酯-四氢呋喃系统与聚苯乙烯-对二甲苯系统配制的涂层液涂覆在不可渗透的钢板上，基于自由体积理论建立了聚合物薄膜干燥模型，预测了不同溶剂体系的浓度分布。夏正斌等[7]将丙烯酸聚氨酯涂料涂覆在马口铁板上，建立了溶剂扩散系数的预测模型，并得出溶剂扩散系数是成膜时间和溶剂浓度的强函数。白贵平[8]将感光乳剂涂覆在相机胶片上，研究干燥过程中，环境空气的温度、湿度以及胶片的移动速度对干燥速率的影响。何苏闽[9]将丙烯酸酯胶黏剂涂覆在玻璃板上，模拟热风条件下，不同干燥温度对胶粘剂干燥过程的影响。然而，这些涂层材料的基材大多是不可渗透的板材，仅研究了溶剂在薄膜-空气界面的扩散。纺织品是一种多孔纤维材料，溶剂在织物上的扩散机理不同于在非渗透基材上的扩散机理。溶剂扩散发生在薄膜-空气界面和基材-空气界面。在涂层织物的固化过程中，溶剂扩散的机理还没有得到很好的研究。

本文研究聚甲基丙烯酸甲酯（PMMA）/丙酮涂层玻璃纤维织物在固化过程中的溶剂扩散机理。利用有限元软件，通过多孔介质传热接口和偏微分方程接口实现了传热-传质-体积收缩的模拟计算，并通过共焦拉曼光谱验证了模型的准确性。利用涂层纺织材料固化过程中溶剂扩散的数值模型，可以获得干燥过程中涂层膜内部不同位置的溶剂浓度、干燥平衡时间和体系中的残留溶剂浓度，探讨涂层厚度和烘干温度对固化过程中溶剂扩散的影响，为涂层纺织材料的制备、性能研究和干燥条件的优化提供理论指导。

1 涂层织物固化过程中溶剂扩散的数学模型

织物是具有交织结构的多孔纤维材料，将PMMA和丙酮溶液配制的涂层液涂覆于玻璃纤维织物表面，涂层液会向织物内部渗透，在固化过程中溶剂从涂膜内部向涂膜-空气界面（Z=L）与基材-空气界面（Z=H）移动，并在表面蒸发。图1 为涂层织物固化过程中溶剂扩散的示意图。

图1 涂层织物固化过程中溶剂扩散的示意图Fig.1 Schematic diagram of solvent diffusion in curing process of coated fabric

涂膜干燥固化过程是传热、传质与体积收缩相互耦合、相互影响的复杂的过程[10]。一方面热量从环境向涂膜内部传递，通过改变涂膜内部温度从而影响传质过程，另一方面由于气液界面的溶剂蒸汽压大于环境中溶剂蒸汽压，使涂膜内部的溶剂不断向大气中扩散，随着溶剂的蒸发，涂层厚度不断减小，当溶剂蒸汽压与空气中溶剂蒸汽压相等时，扩散达到平衡状态。因此，固化过程需要同时考虑涂膜内部的热量传递、质量传递和体积收缩过程。为模拟涂层玻纤织物固化过程中的溶剂扩散机制，建立了如下假设：

（1）忽略了涂层液的渗透过程，认为涂层液在织物内渗透完毕后开始的薄膜固化。

（2）不考虑纱线对涂层液的毛细作用，涂层液仅存在于纱线与纱线之间的孔隙中。

（3）涂层织物固化过程中环境的温度、风速恒定。

（4）涂层液和织物的热物性参数为定值。

1.1 涂层织物的传热理论

由于织物为多孔材料，涂层液会渗透到织物的孔隙中，织物内的传热应采用多孔介质的传热方程，在多孔介质中涂层液和纱线的热物理属性被组合为有效特性，即有效体积热容和有效导热率。在干燥过程中，织物内的能量变化主要是由溶剂扩散引起的，其能量守恒方程[11-12]如公式（1）：

式中：ρ为密度；cp为恒压热容eff；（ρcp）eff为有效体积热容；keff为有效导热系数；θp为织物的孔隙率；T 为温度；c 为溶剂的瞬时浓度；x 和 y 为位移；Di为涂层液体系中溶剂的互扩散系数。式中（ρcp）eff和keff的计算公式如下：

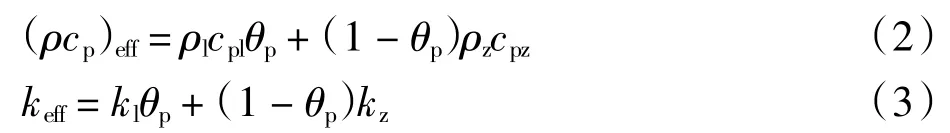
式中：ρl和cpl分别表示涂层液的密度和比热容；ρz和cpz分别表示织物的密度和比热容；kl和kz分别表示涂层液和织物的导热系数。

织物上方的涂层液不是多孔材料，因此采用流体传热方式，其能量守恒方程[11-12]为：

等式左边表示涂层液体系单位时间内增加的能量，等式右边第1 项及第2 项分别表示涂层液体系内导热传递的热量和溶剂扩散所携带的热量。

1.2 固化过程中的传质理论

溶剂分子的扩散过程是随时间变化的非稳态扩散，符合菲克扩散的第二定律[13]，传质控制方程如公式（5）：

式中：c 为丙酮扩散时的瞬时浓度；x 和y 分别为水平方向和垂直方向上的扩散；t 为时间；Di为涂层液体系中溶剂的互扩散系数，表征溶剂分子扩散能力的物理量，它能准确反映溶剂小分子在聚合物中的扩散行为[14]。计算过程为：

式中：D1为自扩散系数；φs为溶剂的体积分数；χ为溶剂聚合物体系的相互作用参数；D0是指前因子；R =8.314 J/（mol·K），为气体常数；T 为热力学温度；ws和wp分别为溶剂和聚合物的质量分数；分别为溶剂和聚合物的临界空穴自由比容；ξ为溶剂和聚合物迁移单位摩尔体积的比值为溶剂和聚合物的自由体积；γ为重叠因子，取值范围是0.5~1，表明不同的迁移单位可跳跃到同一个空穴空间；E 为扩散活化能。Reis 等[15]利用公式（8）来求解扩散所需活化能。

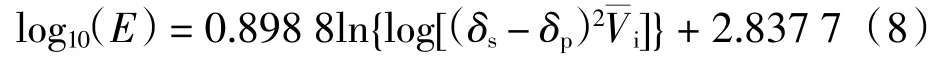
式中：δs和δp分别为溶剂和聚合物的溶解度参数；为溶剂的摩尔体积。

1.3 涂层收缩与时间的依赖关系

在涂层织物干燥过程中，溶剂不断向空气中扩散，导致涂膜厚度不断减小。根据溶剂质量平衡方程将涂层厚度的收缩率与溶剂的蒸发率联系在一起，建立了涂层厚度随时间变化的方程[16]，如公式（9）：

式中：kg是传质系数，通过Chilton-Colburn 类比法得到[17]；VS为溶剂的比容，它和密度互为倒数为周围环境中溶剂的蒸汽压，其值近似为0，因为溶剂的扩散不会使环境中溶剂浓度明显升高[18]为涂膜体系中的溶剂分压，通过Flory-Huggins 理论进行求解[16]，如公式（10）：

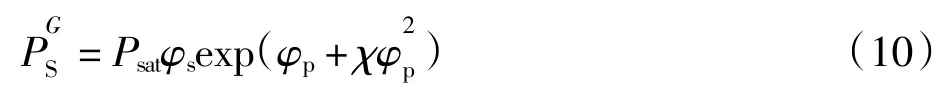
式中：φs和φp分别为溶剂和聚合物的体积分数；Psat为溶剂的饱和蒸汽压，通过Antoine 方程得到，如公式（11）：

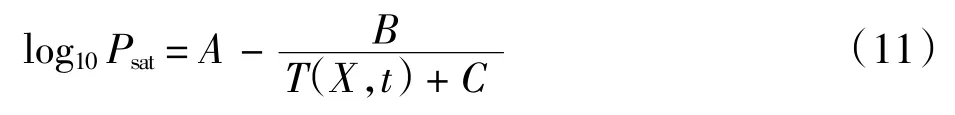
式中：A =6.394 858；B=1 292.466；C=238.240 9。A、B、C 均为 Antoine 常数[19]。

2 溶剂扩散模型的求解条件

2.1 初始条件及模型参数的设置

在环境风速为0.095 m/s 的条件下，针对初始温度为298.15 K、溶剂质量分数为80%和初始涂层厚度为960 μm 的涂层织物体系，进行干燥固化过程的数值模拟，计算过程中所需的自由体积参数如表1 所示。

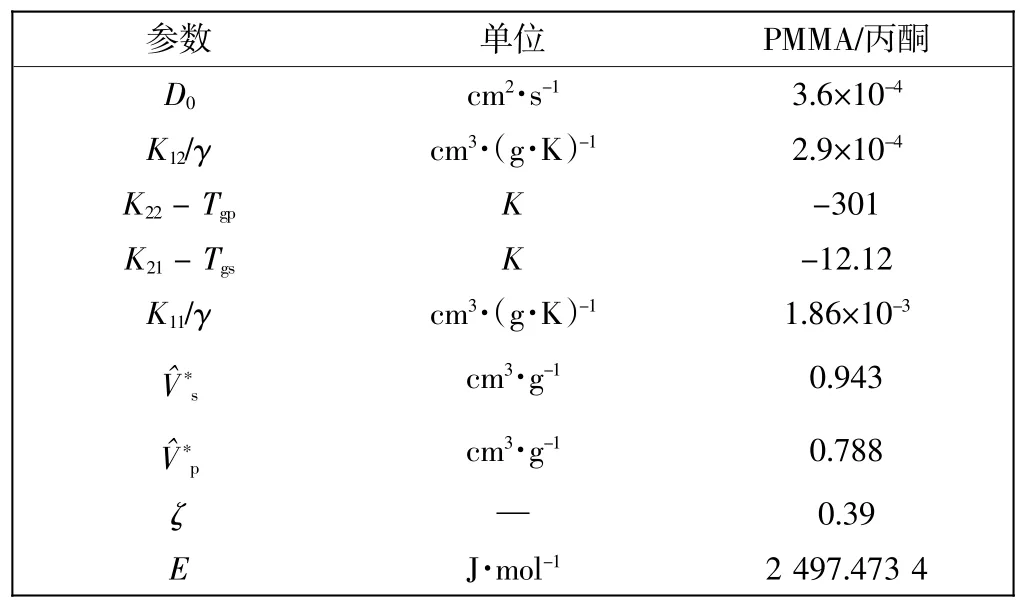
表1 溶剂-聚合物体系的自由体积参数Tab.1 Free volume parameters of solvent-polymer system

2.2 传热过程边界条件的设置

涂层织物在烘箱中干燥时，由于织物孔隙率的存在，涂层液会渗透到织物孔隙中，因此织物与空气界面和涂层液与空气界面都会和周围的热空气进行热量传递。

在Z=L 处（涂层液与空气界面），边界方程为：

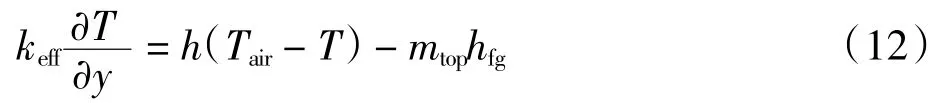
在Z=H 处（织物与空气界面），边界方程为：

式中：h 为表面自然对流的换热系数；Tair为空气温度；T 为涂层织物温度；hfg为蒸发潜热；θp为织物的孔隙率；mtop和mbottom分别为顶部和底部的蒸发率，计算方程为：

2.3 传质过程边界条件的设置

涂层织物干燥过程中，溶剂的扩散通量可由传质系数及扩散推动力表示。

在Z=L 处（涂层液与空气界面），边界处的通量方程为：

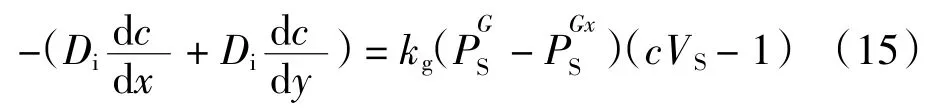
在Z=H 处（织物与空气界面），边界处的通量方程为：

式中：Di为聚合物体系中溶剂的互扩散系数；c 为聚合物体系中溶剂的瞬时浓度；VS为溶剂的比容；θp为织物孔隙率。

3 结果与讨论

3.1 涂层织物溶剂扩散模型的计算结果

利用上述建立的干燥过程中溶剂的扩散模型，可以预测涂膜内部任意位置处溶剂浓度的分布情况和涂层液体系中溶剂互扩散系数随时间的变化曲线，计算结果如图2、图3 所示。

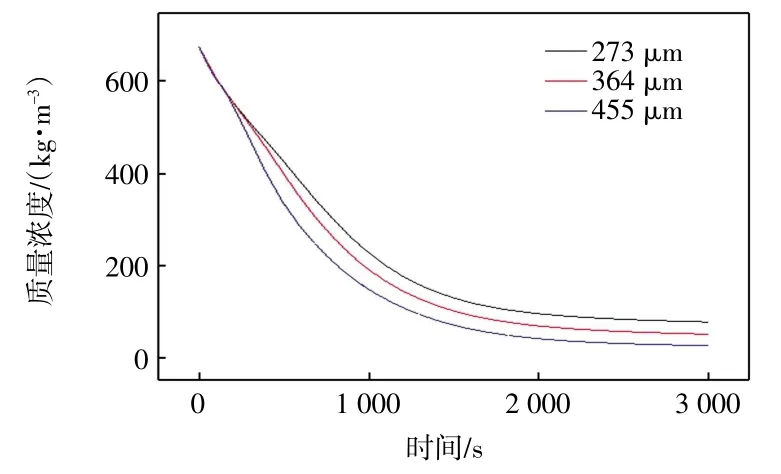
图2 距织物表面273、364 和455 μm 处溶剂浓度分布Fig.2 Distribution of solvent concentration at 273，364 and 455 μm away from fabric surface

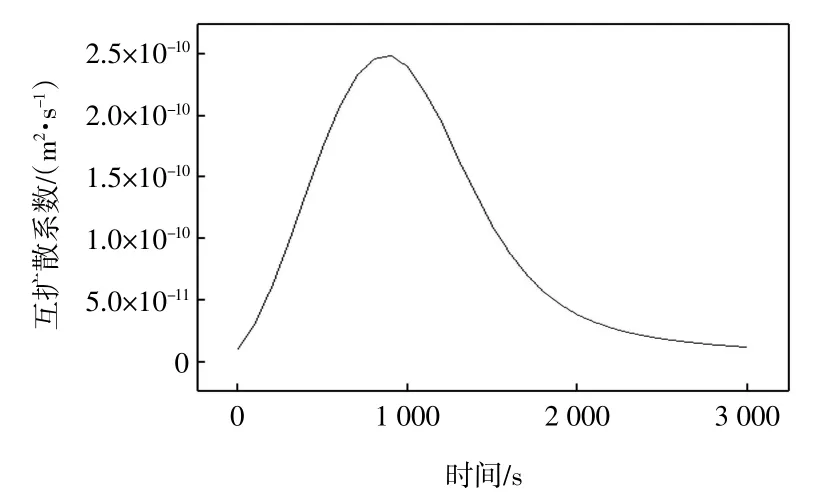
图3 互扩散系数随时间的变化曲线Fig.3 Time dependence curve of interdiffusion coefficient

由图2 可知，涂膜内部不同位置处的溶剂浓度均是随时间的延长不断减小，且在2 000 s 左右，溶剂浓度趋于恒定，说明该条件下涂层液的固化过程基本完成，此时涂膜内部平均残留溶剂浓度为51.528 5 kg/m3。此外，在相同的干燥时间下，距离织物表面455 μm 处的溶剂浓度比距离织物表面273 μm 处的溶剂浓度下降的幅度大。这主要是因为溶剂扩散的推动力是二相体系中溶剂的蒸汽压与大气中溶剂的分压之差和体系中的浓度梯度，溶剂蒸发发生在液体-空气界面，溶剂分子从液体-基材界面向液体-空气界面迁移，距空气侧越近浓度梯度越大，扩散越快。

由图3 可知，在溶剂聚合物的体系中互扩散系数随着时间的延长表现出先增后减的趋势，在1 000 s 左右达到最大值，这是因为扩散初期，体系中溶剂浓度较高，浓度梯度较大，溶剂蒸汽压与环境蒸汽压差值较大，溶剂扩散较快；而在扩散后期，体系中溶剂较少，溶液粘度较大，扩散推动力主要由内部溶剂浓度梯度决定，扩散阻力较大。

3.2 结果验证

验证实验利用激光共聚焦拉曼光谱仪，获得了单一丙酮溶液、PMMA 固体和不同溶剂质量分数的涂层液的拉曼光谱图。涂层溶液中丙酮和PMMA 的特征峰分别为 786.6 μm 和 811.4 μm。根据 PMMA、丙酮的峰强比与二者质量比的关系，绘制浓度的校准曲线[20]，如图4 所示。W(i)为涂层液中溶剂或聚合物的质量分数，I(i)为涂层液中溶剂或聚合物的峰强。

图4 PMMA/丙酮相对峰强比与质量比的关系Fig.4 Relationship between relative peak intensity ratio and mass ratio of PMMA/acetone

建立的浓度校准方程为：

其中，线性相关系数R2=0.990 7，说明拟合程度较高。利用浓度校准曲线，通过拉曼光谱仪测试了涂膜内部距织物表面273、364 和455 μm 处不同时间下的溶剂浓度分布情况，并与模拟浓度进行对比，结果如图5 所示。

图5 溶剂浓度的模拟值与实验值的对比图Fig.5 Comparison of simulated and experimental values of solvent concentration

由图5 可知，在2 000 s 前，溶剂浓度的模拟值和实验值均随时间的延长快速下降；而2 000 s 后涂层液的浓度趋于稳定，说明该条件下大约需要2 000 s 来完成涂层液的固化。另外，溶剂浓度的实验值与模拟值的吻合程度较高，在干燥前期（0～1 000 s），涂层液距离织物表面273、364 和455 μm 处模拟值与实验值的平均相对误差分别为10.39%、11.3%和14.9%。在干燥后期溶剂浓度的模拟值略高于实验值，这可能是因为利用模型计算时把溶剂-聚合物体系的自由体积参数当成了定值，忽略了浓度对自由体积参数的影响。事实上，Hong[21]提出的自由体积参数会随着溶剂浓度的减小而减小，从而利用自由体积理论预测的扩散系数偏小，导致模型预测的扩散过程稍慢，干燥时间稍长。

3.3 涂层厚度对溶剂扩散的影响

在温度 80 ℃、风速 0.751 4 m/s（DGP-9057B-2 型鼓风干燥箱的风速）、溶剂质量分数为80%的条件下对平纹涂层织物进行干燥固化模拟，研究初始厚度为0.1～1.2 mm 的涂层液对溶剂扩散的影响，结果如图6所示。

图6 不同涂层厚度下溶剂浓度的变化Fig.6 Change of solvent concentration under different coating thickness

由图6 可知，涂层越厚，浓度时间曲线的斜率越小，溶剂扩散越慢，随着涂层厚度从0.1 mm 增加到1.2 mm，干燥平衡时间逐渐从600 s 增加到1 700 s，涂层厚度与干燥时间的关系如图7，二者的拟合方程为：

图7 干燥平衡时间与涂层厚度的关系Fig.7 Relationship between drying equilibrium time and coating thickness

其中拟合因子R2=0.991 38，拟合程度较高，利用此方程可以预测任意涂层厚度下的干燥时间，为工业化生产提供理论指导。

涂层厚度与时间的关系如图8 所示。

图8 涂层厚度与时间的关系Fig.8 Relationship between coating thickness and time

由图8 可见，涂层厚度在干燥过程不断减小，干燥达到平衡时涂层厚度远低于初始厚度。干燥厚度与初始厚度的关系如图9 所示。

随着初始涂层液厚度的增加，在扩散达平衡时干燥厚度也表现出上升的趋势，二者的关系方程为：tb=-0.014 39+0.352 79x+0.088 15x2，其中拟合因子R2=0.999 63，由此模型可得到想要涂层厚度的初始厚度。

3.4 烘干温度对溶剂扩散的影响

温度会影响溶剂的蒸汽压、传热系数和传质系数，从而影响溶剂扩散的快慢。在溶剂质量分数为80%、风速 0.751 4 m/s、涂层厚度为 960 μm 的条件下，根据PMMA 的玻璃化温度为111.4 ℃，设置温度梯度为 25、50、80、100 和 120 ℃，研究烘干温度对溶剂扩散的影响，计算结果如图10 所示。

由图10 可知，在相同的时间内，温度越高，溶剂浓度降低的幅度越大，溶剂扩散的越快。在扩散达平衡时，温度为 25、50、80、100 和 120 ℃的涂层液体系中残留溶剂浓度分别为 56.567 03、41.946 6、29.723 89、22.735 28 和16.622 65 kg/m3，说明温度越高，体系中的残留溶剂越少，干燥越充分。随着烘干温度从25 ℃增加到120 ℃，平衡干燥时间逐渐由1 600 s 降低到1 000 s，烘干温度与干燥时间的关系如图11 所示。二者的拟合方程如下：

其中，拟合因子R2=0.993 9，拟合度较高。由图11 可知，温度越高，扩散达平衡时所需的时间越短。当温度为 120 ℃时（T ＞ Tg），虽然薄膜的干燥时间缩短，但容易使薄膜泛黄，脆性增大。当温度介于80～100 ℃时，溶剂扩散较快，且干燥时间降低的幅度变小。因此在考虑聚合物的玻璃化温度并保证涂膜质量和干燥速率的前提下，对于PMMA-丙酮体系的烘干温度建议为80 ～ 100 ℃。

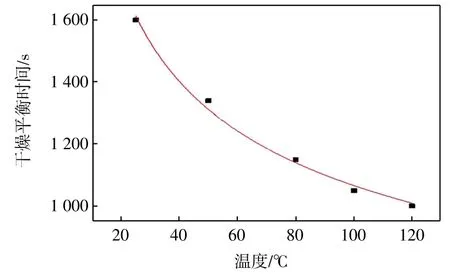
图11 干燥时间与温度的关系Fig.11 Relationship between dry time and temperature

4 结 论

通过建立涂层织物干燥过程中溶剂的扩散模型，探明了多孔介质中溶剂扩散的内在机制，揭示了涂层织物固化过程中涂层厚度对薄膜固化过程中溶剂扩散的影响规律，并通过激光共聚焦拉曼实验对模型进行验证，得出结论如下：

（1）在距织物表面 273、364 和 455 μm 处模拟值与实验值的平均相对误差分别为10.39%、11.3%和14.9%，表明溶剂扩散模型吻合程度较高，可用于预测涂层织物干燥过程中溶剂浓度的分布情况。

（2）涂层越厚，溶剂扩散越慢，且随着涂层厚度的增加干燥时间延长，涂层厚度与干燥时间的拟合方程为tb=570.711+193.831 9x+639.345 2x2。

（3）初始涂层厚度越厚，在扩散达平衡时，干燥厚度也越厚，初始涂层厚度与干燥涂层厚度的关系为tb=-0.014 39+0.352 79x+0.088 15x2。

（4）温度越高，溶剂扩散的越快，体系中残留溶剂越少，干燥越充分。烘干温度与干燥时间的拟合方程为tb=4 236.72T-0.2998。