基于不确定及扰动估计算法的永磁电机控制方法

张国政，张明明，李新旻，谷 鑫

（天津工业大学 电气工程与自动化学院，天津 300387）

内置式永磁同步电机（interior permanent magnet synchronous motor，IPMSM）具有结构简单、可靠性高、功率密度高等优点，在电动汽车及工业领域得到了广泛应用。然而，当永磁同步电机在弱磁区运行时，电机本体及控制系统中逆变器存在的非线性因素等会造成电流谐波，从而导致转矩波动增大，造成电机驱动系统的控制性能下降。因此，改善永磁同步电机的弱磁性能成为研究热点之一。

常用的弱磁控制方法可以分为前馈弱磁、反馈弱磁及混合弱磁控制。具体而言，前馈弱磁控制有基于模型的公式计算法[1]、查表法[2]、梯度下降法[3-4]；反馈弱磁控制主要包括负直轴电流补偿法[5-6]、单电流调节器控制法[7-9]、相角法弱磁控制[10]等。文献[11]对比了常见的前馈弱磁控制及反馈弱磁控制，表明2 种方法均有效地扩展了永磁同步电动机的恒功率区域，而前馈法在弱磁区能产生更大的转矩，提供更宽的恒功率范围。

永磁同步电机控制系统中的谐波问题会导致转速、转矩波动增大，增加电机的振动及噪声，影响电机寿命[12]。为减小谐波，文献[13]从电机本体设计出发，提出利用槽口偏移消除特定次数的齿槽转矩谐波。文献[14]建立了速度反馈律，通过自适应地估计模型参数，达到降低谐波含量，抑制转矩脉动的目的。文献[15]用谐波注入法来消除电流谐波，减小转矩波动，但该方法需提前了解电机运行条件，不能很好地满足负载发生变化的情况。

不确定性及扰动估计（uncertainty and disturbance estimator，UDE）控制理论自提出以来已成功应用于诸多领域[16-18]。文献[16]将UDE 控制器应用于双向非逆变降压变换器的电感电流控制中，并给出了有限控制带宽约束下UDE 控制器的最佳设计准则。文献[17]将UDE 控制应用于网侧LCL 逆变器的电流控制中，提高了控制器对于周期性干扰信号的抑制作用。文献[18]在表贴式永磁同步电机的驱动与控制中涉及了基于UDE 的电流控制器，并给出了控制器参数整定方法，但仅适用于id=0 的控制方式。

为了解决永磁同步电机在弱磁区参数非线性变化、电流谐波含量大的问题，本文将延时滤波器与UDE 控制理论相结合，提出了一种新的应用于弱磁工况下的电流谐波抑制策略。本文以20 kW 内置式永磁同步电机为被控对象，通过仿真验证了所提弱磁控制算法的有效性。

1 PMSM 弱磁原理与电流谐波分析

1.1 PMSM 弱磁原理

忽略磁饱和、磁滞效应及涡流损耗，在dq 坐标系下，内置式永磁同步电机的电压方程及转矩方程如式（1）、式（2）所示：

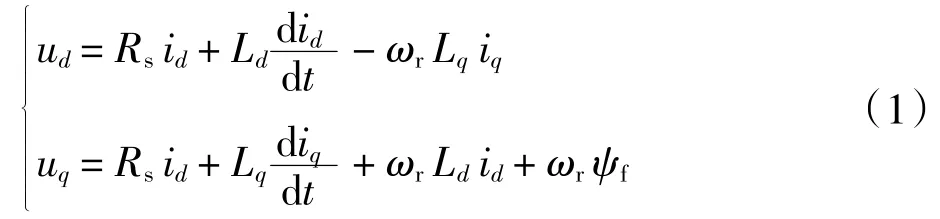
式中：Rs为定子电阻；Ld、Lq为 d、q 轴电感；ωr为转子电角速度；ud、uq为 d、q 轴电压；id、iq为 d、q 轴电流；ψf为电机永磁体磁链；p 为电机极对数；Te为电磁转矩。

当电机工作在额定转速以下时，通常采用最大转矩电流比（maximum torque per ampere，MTPA）控制，从而减小铜耗，提高电机效率。此时，d 轴电流给定值由式（3）决定：

随着转速升高，电机反电动势不断增大。但电机运行的电压幅值us及定子电流幅值is受逆变器容量的限制，即存在电压极限Usmax及电流极限Ismax，因此d、q 轴电压电流需要满足式（4）、式（5）所示的约束条件：

忽略定子电阻压降，结合电压方程及电压电流约束条件，当电机工作在弱磁区时，d 轴电流的给定值由式（6）决定：

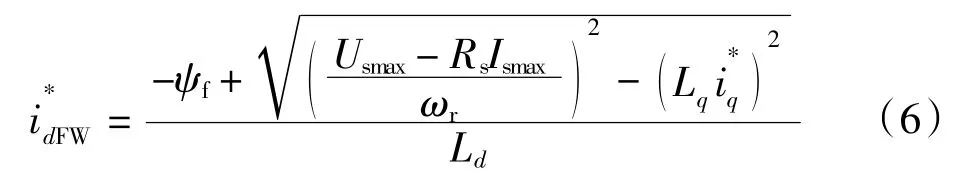
在永磁同步电机驱动控制系统中，当电机转速小于基速时，电机工作在恒转矩区，采用MTPA 控制，d 轴电流给定值由式（3）决定；当电机转速大于基速时，电机工作在恒功率区，采用弱磁控制，d 轴电流给定值由式（6）决定。永磁同步电机弱磁控制转速-电流双闭环控制框图如图1 所示。

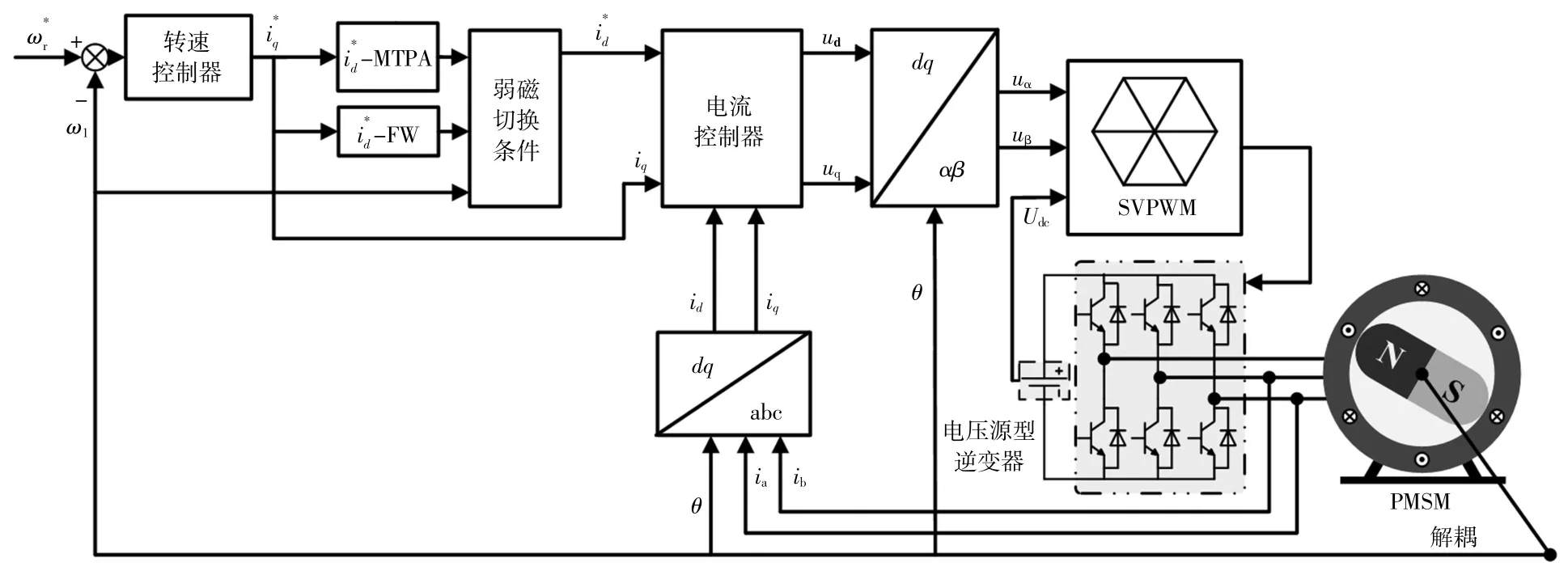
图1 永磁同步电机弱磁控制转速-电流双闭环控制框图Fig.1 Speed-current dual closed-loop control diagram of flux-weakening control for PMSM

1.2 电流谐波分析

在永磁同步电机弱磁控制中，一些非理想因素会形成电流谐波，产生转矩波动。

1.2.1 永磁体谐波因素

由于永磁体制造及工艺上的限制，其实际产生的转子磁场在气隙中并非呈理想正弦分布。永磁体磁链除了包含永磁体产生的基波磁链ψ1外，还包括基波磁链的 3 次谐波 ψ3、5 次谐波 ψ5[19]。

利用坐标变换，可得到考虑高次谐波的d、q 轴磁链表达式如下：

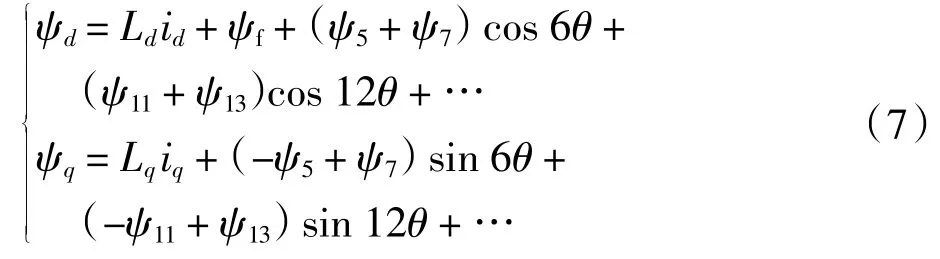
由式中可以看出，d、q 轴磁链中出现了随位置角变化的6k 次谐波磁链。考虑永磁体谐波的影响，IPMSM 弱磁区下的电压、电流约束条件如下：

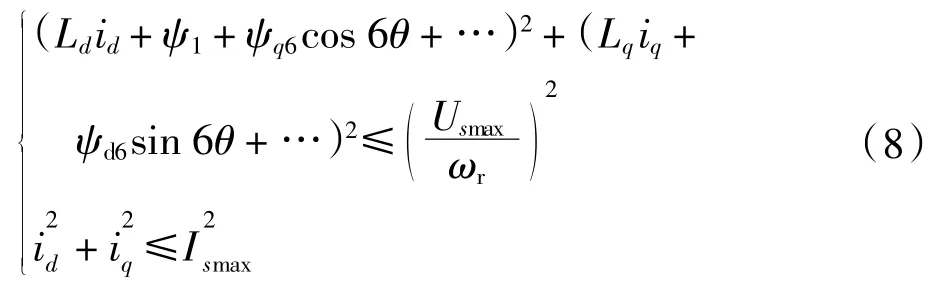
可见，在弱磁工况下d、q 轴电流中包含6 倍频谐波分量[20]。

1.2.2 逆变器非线性因素

图2 所示为永磁同步电机弱磁区电压逆变器非线性示意图。当电机工作在弱磁区时，受逆变器中死区效应、开关管压降等非线性因素的影响，使得电压六边形边界向内缩小，实际电压轨迹不再是电压六边形的内切圆[21]，如图 2（b）所示。

图2 永磁同步电机弱磁区电压逆变器非线性示意图Fig.2 Inverter nonlinearity effects on voltage applied to PMSM drives in flux-weakening region

（1）死区效应造成的电压误差在d、q 轴下的表达式为：

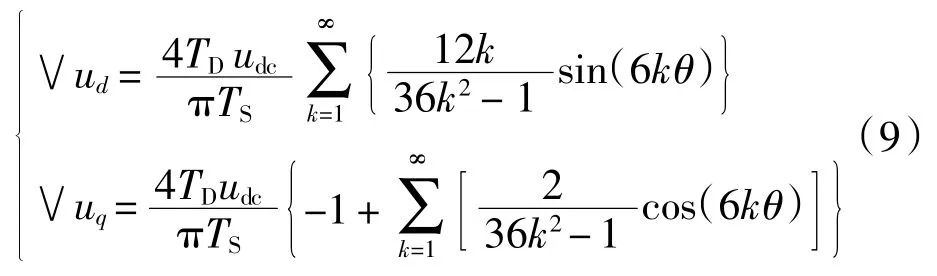
式中：TD为死区时间；TS为控制周期；udc为逆变器直流母线电压。由式（9）可得，d、q 坐标轴下的电压误差包含直流分量及因死区效应产生的6 倍频谐波分量。

（2）考虑逆变器开关管管压降的实际电压矢量与参考电压矢量间的误差电压为：

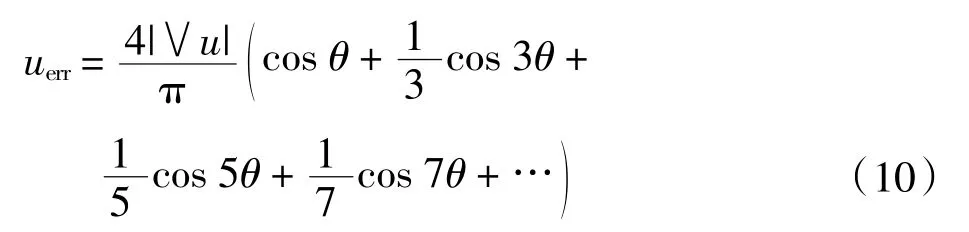
式中：Δu 为一个控制周期内的平均误差电压。

由式（10）可以看出，由开关管压降造成的误差电压存在奇次谐波，但经坐标变换到dq 轴坐标系下，仍转化为6 倍频谐波信号。

2 基于UDE 的控制器设计

UDE 控制的基本原理是通过设计一个合适的滤波器，估计未知的干扰信号，将其用于合成鲁棒控制器。基于UDE 理论设计出的控制器主要包括参考模型微分、误差跟踪、实际模型逆三部分，其结构图如图3 所示。由第1.2 节分析可知，在弱磁控制中电流环往往受磁场和逆变器非线性因素影响，而含有6 倍频谐波信号。本文在设计电流控制器时把该信号视为干扰项，通过设计合适的扰动估计器进行补偿，实现电流谐波抑制的目的。

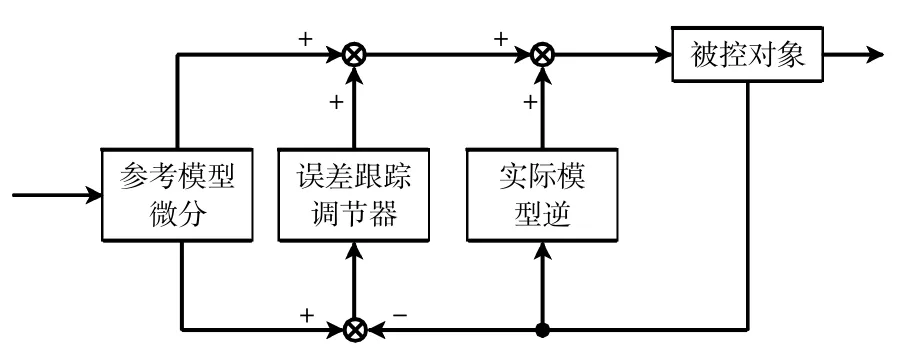
图3 基于UDE 的控制系统结构Fig.3 Schematic diagram of UDE control system

2.1 含扰动因素项的永磁电机模型

由IPMSM 的电压方程，建立包含有未知干扰项的电机模型，其矩阵形式如式（11）所示：

2.2 基于UDE 算法的参考模型及误差方程

对于弱磁控制下的IPMSM 而言，为了实现电流环d、q 轴实际电流对给定电流的良好跟踪，选择期望的参考模型定义如下：

式中：xm=[idm，iqm]T为参考状态矢量为参考给定指令。通过选择合适的系数矩阵Am、Bm使得控制器能够满足电流响应性能。

对于IPMSM 而言，由于交直轴电感不同，设计系数矩阵形式如下：

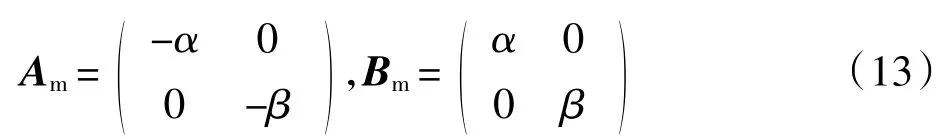
式中：α、β为相互独立的2 个正实数。

为了实现d、q 轴电流的稳定跟随，需要状态矢量x（t）收敛至其参考轨迹 xm（t），即跟踪误差逐渐收敛至0。定义跟踪误差方程如下：

由此得到输入矢量u（t）为：

其中，ud（t）=f（t）+d（t），它是由电机参数扰动及包含电流谐波在内的系统扰动两部分组成，称之为集总扰动。

将电压控制率代入到系统实际模型的状态方程中，化简整理得：

由 Am特征值-α <0，-β <0 得，误差方程是渐进稳定的，即：采用上述电压控制率的结构，能保证电机实际电流稳定跟踪参考电流。

2.3 改进UDE 的电压控制率

针对电机系统中存在的阶跃扰动信号，采用一阶低通滤波器对集总扰动进行估计，传递函数为：

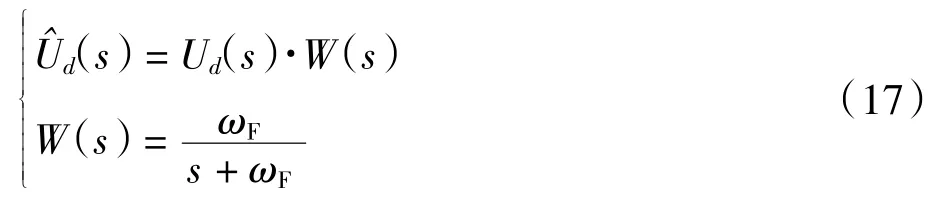
式中：W（s）为一阶低通滤波器的 s 域表达式；ωF为一阶低通滤波器的截止频率。

针对弱磁控制中，永磁同步电机控制系统电流环存在6 倍频谐波的问题，引入延时滤波器（time delay filter，TDF）对集总扰动进行估计，实现对电流谐波的抑制作用。

在式（17）的基础上结合延时滤波器，得到含有6倍频扰动信号的集总扰动估计如式（18）所示：

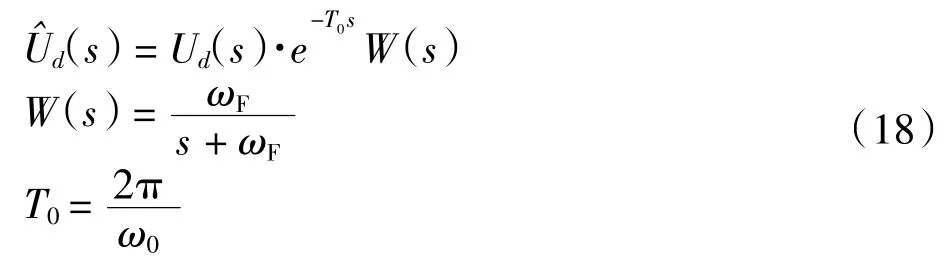
式中：ωF为一阶低通滤波器的截止频率；ω0为延时滤波器所要抑制的谐波频率。以被试电机为例，电机极对数p =4，当电机运行于弱磁区转速6 000 r/min 时，基频为400 Hz，此时6 倍频扰动信号为2.4 kHz。由式（19）得，一阶低通-延时滤波器的闭环传递函数bode图如图4 所示，由图4（b）可以看出，6 倍频谐波处具有很高增益。

图4 一阶低通-延时滤波器闭环传递函数bode 图Fig.4 Bode diagram of closed loop transfer function of first-order low-pass-delay filter

将式（18）的集总扰动估计代入到式（15）的备选电压控制率中，得：

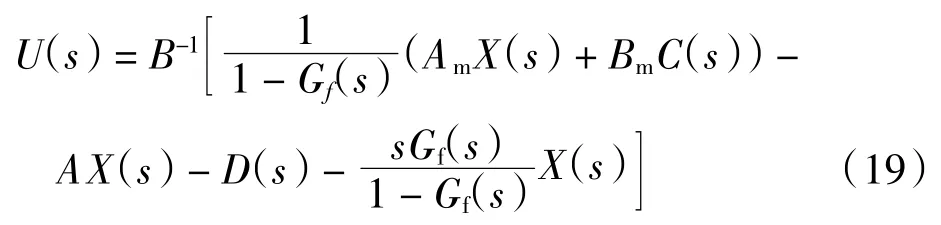
式中，Gf（s）表达式如下所示：

经化简整理，得到含延时滤波器的UDE 电压控制率如式（21）所示：

将 Gp、Gi代入到式（21）中，即可得到能够抑制倍频谐波的永磁同步电机电流环UDE 控制器。如式（21）所示，UDE 控制器参数包括参考模型参数α、β，一阶低通滤波器截止频率ωF以及延时滤波器参数T0。其中，α、β根据参考模型微分部分的跟踪效果整定，一阶低通滤波器截止频率ωF根据误差跟踪调节器部分idm、iqm的跟踪性能整定，延时滤波器参数T0由式（18）计算得到。以d 轴为例，采用延时滤波的UDE 控制器原理图如图5 所示。

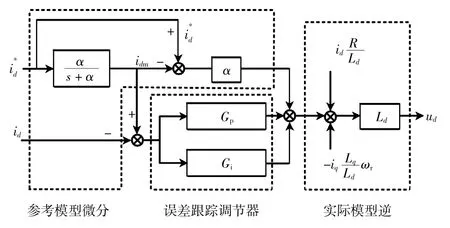
图5 采用延时滤波的UDE 控制器原理图Fig.5 Schematic diagram of UDE controller using TDF

由图5 可知，采用延时滤波的UDE 控制器主要包含参考模型微分、误差跟踪调节器、实际模型逆3 部分，分别与式（21）相应序号对应。其中，参考模型的微分前馈环节可以加快误差收敛过程；误差跟踪调节器对集总扰动进行准确估计，用于补偿实际模型与参考模型的跟踪误差；实际模型逆模块抵消了永磁同步电机的已知模型部分。与PI 控制相比，UDE 控制器含有微分项，能够获得更佳的控制性能。

3 弱磁切换策略

在弱磁控制中，电机是否进入弱磁状态的判断条件主要有转速判断和电压判断2 种，一般通过电机当前转速或者定子电压判断是否进入弱磁状态。

以固定转速作为弱磁切换条件时，首先计算得到恒转矩区及恒功率区的转折速度，然后利用电机实时转速与转折速度作对比，判断电机是否进入弱磁状态。这会造成计算方式在之间的频繁切换，从而形成较大的转矩波动

以电压作为弱磁切换条件时，通过实时监测定子电压Us是否超过逆变器直流侧的最大电压Usmax，来判断电机是否进入弱磁区域。为保证控制器的可靠性，通常利用最大电压Usmax与定子电压Us的差值△U = Usmax-Us与某一固定阈值做对比。阈值的整定过程较为繁琐，且为保证弱磁切换的可靠性，阈值会一定程度上牺牲直流母线电压的利用率，无法提供更宽的弱磁区范围。

因此，设计一种新的弱磁切换方法，逻辑如下。

情况1：当电机转速达到转折速度，且电压差满足条件时，d 轴电流的给定方式由切换至

情况2：当电机转速小于转折速度，且电压差不满足条件时，d 轴电流的给定方式由切换至

情况3：若电机转速达到转折速度，但电压差不满足条件，系统仍能以最大功率运行在MTPA 状态，此时d 轴电流给定值仍保持

情况4：若电机转速小于转折速度，但电压差满足条件，此时系统已经达到饱和，d 轴电流给定值由切换至

该弱磁切换策略的逻辑规则如表1 所示。

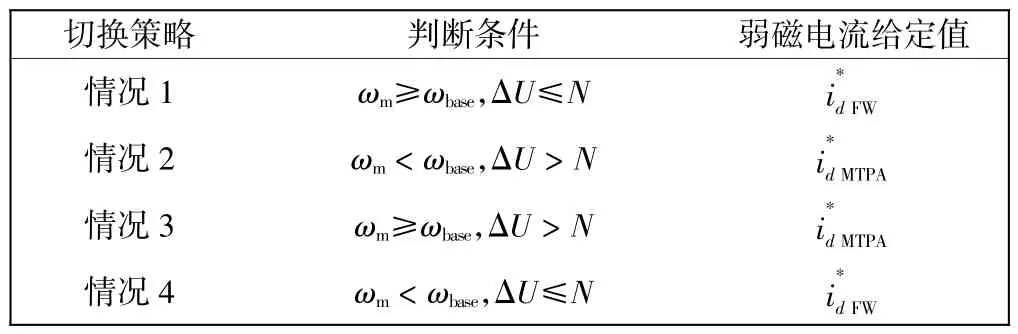
表1 所提弱磁控制切换策略Tab.1 The proposed field weakening control switching algorithm

在该切换策略下，相当于为固定转速的切换点增加了以电压差为环宽的滞环比较器，从而避免了以固定转速进行弱磁切换时带来的算法频繁切换、转矩波动大的问题。以被试电机为例构建仿真模型，转速给定方式为斜坡给定，恒转矩区与恒功率区的切换转速为4 500 r/min，滞环比较器的环宽N=10，仿真结果如图6 所示。

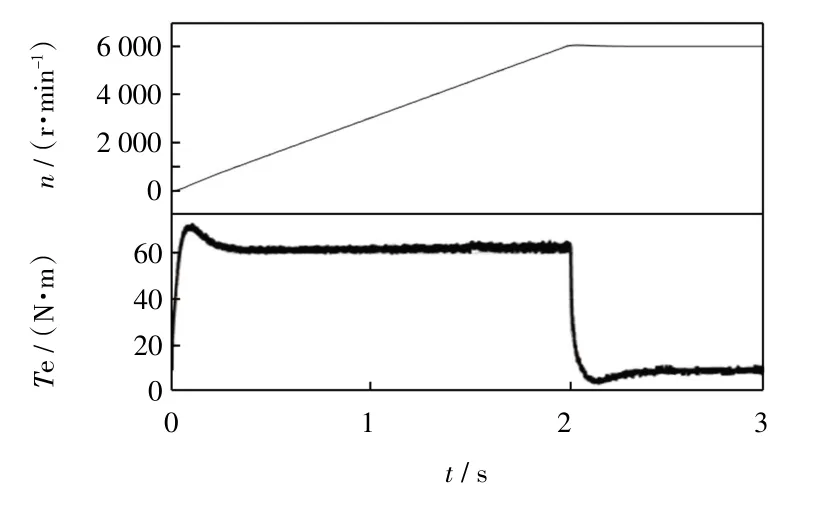
图6 所提方法仿真结果Fig.6 Simulation comparison of proposed method

图6 可以看出，在1.5 s 左右电机转速达到4 500 r/min，开始由恒转矩区进入到弱磁区。仿真结果表明，在所提出的弱磁切换策略下，电机升速平稳，转矩无明显波动，有效实现了弱磁控制下的平滑切换。

4 仿真结果与分析

为了验证所提出的基于UDE 理论设计的电流控制算法的有效性，针对一套20 kW 内置式永磁同步电机进行了仿真分析。仿真系统参数如表2 所示。仿真系统中，开关频率设定为10 kHz，直流母线电压为320 V。

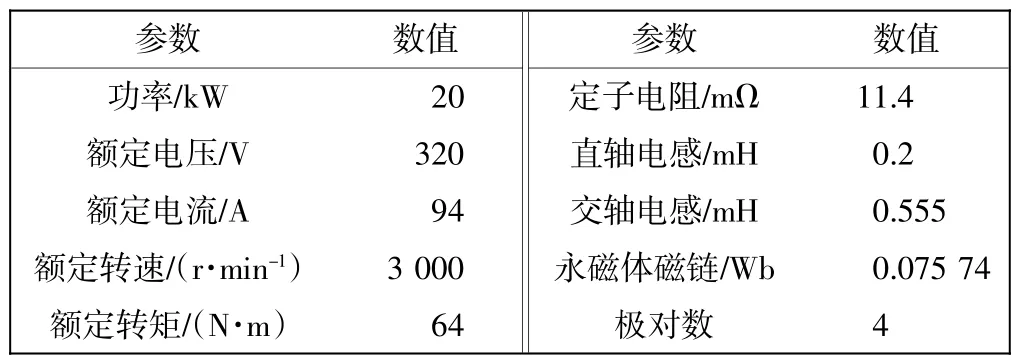
表2 仿真电机参数Tab.2 Parameters of tested IPMSM

仿真结果如图7 所示。仿真中电机转速给定方式选择斜坡起动，斜率为1 s 升速3 000 r/min，目标转速6 000 r/min，对应加速过程中的负载转矩为62 N·m。

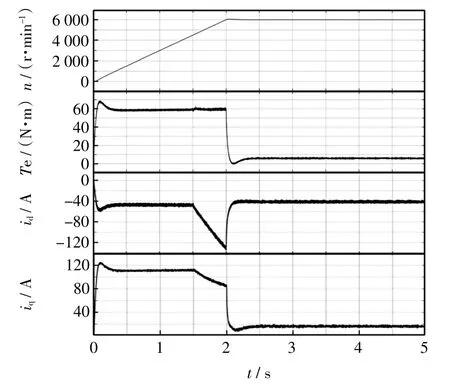
图7 所提控制策略可行性仿真Fig.7 Feasibility simulation of the proposed control strategy

从图7 可以看出，在采用本文所提出的UDE 弱磁控制策略时，电机能够平稳运行，电流实际值能够稳定、准确跟踪给定值，转矩波动小。同时，在1.5 s 左右电机转速达到4 500 r/min 时，电机由恒转矩区进入到弱磁区时，过渡平滑，不存在转速波动及明显的转矩波动。

图8 为不同控制策略下永磁同步电机弱磁运行的仿真结果，（a）、（b）别给出了 PI 控制与本文所 UDE控制的仿真结果。PI 控制下的控制器参数为：Kpd=2πfNLd=0.251，Kpq=2πfNLq=0.697，Kid=Kiq=2πfNRs=14.326[22]。UDE 控制下的控制器参数为：α =8 500，β =4 500，ωF=0.000 03，T0=0.002 6。转速 n，dq 轴电流 id、iq，转矩Te及相电流ia的仿真波形如图8 所示。

仿真中目标转速6 000 r/min，转速斜坡给定斜率为10 s 升速至6 000 r/min，电机空载起动，5 s 时负载转矩阶跃为 30 N·m。对比图 8（a）、图 8（b）可以看出，传统PI 控制下电机在1.5 s 进入弱磁区时存在明显的转矩波动，在弱磁区运行时电流波动及转矩波动较大，负载突变时dq 轴电流有明显超调，且与本文提出的UDE 弱磁控制相比，相同负载转矩下电流谐波含量高。PI 控制下，dq 轴电流峰-峰值波动分别为29.7 A和10.5 A，转矩波动的峰-峰值为7.3 N·m，负载转矩为 0 N·m 及 30 N·m 时对应的相电流 THD 分别为28.01%和20.70%；而本文提出的UDE 弱磁控制下，d、q 轴电流峰-峰值波动分别为9.2 A 和7.6 A，转矩波动的峰-峰值为3.2 N·m，负载转矩为0 N·m 及30 N·m时对应的相电流THD 分别为17.73%和9.28%。对比图8（d）中左右两图的FFT 谐波频谱可以看出，负载转矩为 0 N·m 及 30 N·m 时对应的相电流 5、7 次谐波均有明显减小，根据坐标变换理论分析可知，dq 轴系下的定子电流中6 倍频谐波得到了有效抑制。综上，本文所提含延时滤波器的UDE 弱磁控制算法可以有效减小电流波动、转矩波动，抑制电流谐波含量。

图8 不同策略下弱磁控制仿真波形Fig.8 Simulation results for flux weakening control under different strategies

5 结 论

电流谐波含量高、转矩波动大是永磁同步电机弱磁控制中存在的重要问题。针对这一问题，本文分析了电机永磁体及逆变器非线性因素造成的电流谐波，在此基础上采用UDE 控制理论，设计了含有延时滤波器的UDE 电流控制器，实现了对电流谐波的抑制。此外，充分考虑了不同工况下电机转速及定子电压两种因素的影响，为传统PMSM 弱磁切换中固定转速的切换点增加了以电压差为环宽的滞环比较器，实现了电机从恒转矩区向弱磁区的平滑切换。采用一套20 kW 内置式永磁同步电机驱动平台进行仿真，仿真结果表明：

（1）与传统PI 控制相比，采用本文所提出的控制策略时能够使永磁同步电机的d、q 轴电流波动分别降低69%与28%；

（2）与传统PI 控制相比，采用本文所提出的控制策略时能够使永磁同步电机的转矩波动降低56%；

（3）与传统PI 控制相比，采用本文所提出的控制策略时空载下的电流谐波含量降低了37%，带载情况下的电流谐波含量降低了55%；

（4）在使用本文所提出的弱磁切换方法时，能够有效实现永磁同步电机在恒转矩区与弱磁区之间的平滑切换。

综上，本文所提含延时滤波器的UDE 弱磁区谐波抑制策略能够有效削弱弱磁工况下的电流波动及转矩波动，减小电流谐波含量，保证弱磁控制下电机由恒转矩区向弱磁区过渡时的平滑切换，提高电机系统的运行性能。