基于Bresenham算法圆弧的设计与算法分析

唐启见 湖南软件职业学院

一、圆的构建

圆形是在GUI设计过程中不可规避的重要图形，可以通过确定“一点一线”来描述一个圆形，“一点”为圆心，“一线”为圆的半径，圆心确定了圆的位置，半径确定了圆的大小。圆形及圆弧的生成算法主要有数值微分法、Bresenham画圆算法和中点画线法等。

由于圆形是一个对称的结构，不但左右对称，而且中心对称，所以利用Bresenham画圆算法只需要绘制出圆的一段圆弧，然后通过对称复制的方法即可实现整个圆的绘制。首先确定目标圆的圆心，然后以圆心为坐标原点建立对称坐标系，如先绘制第一象限的1/8段圆弧(如图1所示)。设最先确定的逼近像素点Pi-1的坐标为(xi-1,yi-1)，那么在圆弧附近有两个或者多个逼近像素点，如图1中的Si(xi-1+1,yi-1)和Ti(xi-1+1,yi-1-1)点，在这两个点的选择时需要计算这两个点离理论圆弧的距离，选择离理论圆弧比较近的那个点作为圆弧构建的下一个像素点，以此类推，可以形成一段1/8段圆弧。下面来讨论一下Si点和Ti点到理论圆弧的距离，设Si点和Ti点到理论圆弧的距离分别为D(Si)、D(Ti)，计算公式如下：

图1 Bresenham算法构建1/8段圆弧

因为Si点和Ti点的坐标分别为(xi-1+1,yi-1)、(xi-1+1,yi-1-1)，那么Si点和Ti点分别离坐标原点即圆心的距离的平方分别为：(xi-1+1)2+yi-12、(xi-1+1)2+(yi-1-1)2，将它们与圆的半径的平方做差就可以得出Si点和Ti点离理论圆弧的距离大小了。假设Si点在圆弧的外部，Ti点在圆弧的内部。

D(Si)=[(xi-1+1)2+yi-12]-R2

D(Ti)=R2-[(xi-1+1)2+(yi-1-1)2]

令di=D(Si)-D(Ti)，如果di＞0，说明Ti点比Si点更靠近理论圆弧，即选择Ti点更合适；反之选择Si点。

di=D(Si)-D(Ti)=[(xi-1+1)2+yi-12]-2R2+[(xi-1+1)2+(yi-1-1)2] (1)

将i+1代入(1)式中，得：

di+1=[(xi+1)2+yi2]-2R2+[(xi+1)2+(yi-1)2]

将di+1-di，得：

di+1-di=2[(xi+1)2-(xi-1+1)2]+(yi2-yi-12)+(yi-1)2-(yi-1-1)2

如果di≥0，则选择Ti点，即：

xi=xi-1+1，yi=yi-1-1，di+1=di+4(xi-1-yi-1)+10

若di＜0，则选择Si点，即：

xi=xi-1+1，yi=yi-1，di+1=di+4xi-1+6

以此类推，可通过计算di和di+1来对Si和Ti进行取舍。将i=1、x0=0、y0=R代入式(1)中：

d1=3-2R

通过上述讨论可通过Bresenham画圆算法得到第一象限的1/8圆弧，再通过对称复制的方法即可创建整个圆形。

二、椭圆的构建

椭圆与圆的形状的相似性，决定了它们的算法具有一定的相似性。椭圆也是一个对称结构的图形，由于椭圆的对称性相对于圆形的对称性来说有一定的局限性，所以需要把椭圆的在一个象限的1/4段圆弧构建出来，然后再用对称复制的方法形成整个椭圆。首先将坐标原点设为椭圆的中心点，x轴方向的半径设为a，y轴方向的半径设为b，椭圆上的点如下关系：

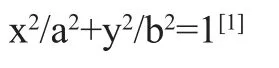
隐式方程式为：

选取第一象限的1/4段椭圆弧来进行讨论，如图2所示，N为椭圆弧上的某个点，N左边的点在区域-1，N右边的点在区域2，设N点的斜率为-1，那么区域1的点的斜率大于-1，区域2的点的斜率小于-1。

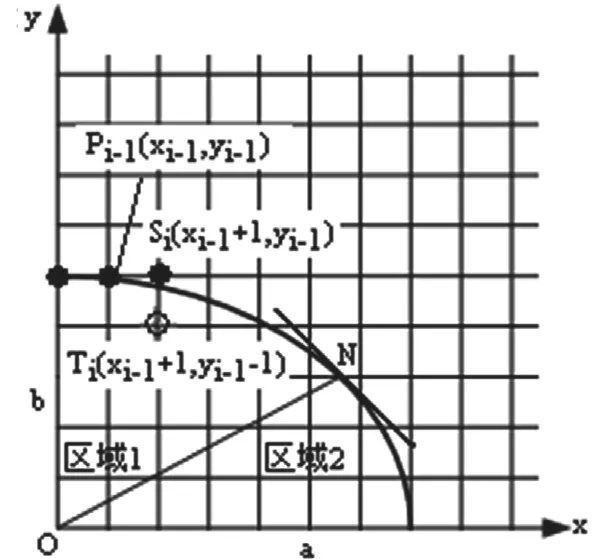
图2 Bresenham算法构建椭圆弧(一)

通过上述分析，以N点为界分为区域1和区域2两个区域，在区域1中，x增长速度比y减小的速度要快，所以选取x轴为基轴进行讨论，反之在区域2中，x增长速度比y减小的速度要慢，所以选取y轴为基轴进行讨论。无论是在区域1作图时随着x的不断加1，y是否作减1？还是在区域2作图时随着y的不断减1，x是否作加1？都需要通过计算来决定。若在区域1作图时，每确定一点后都需要判断是否到达N点。如果到达N点，就需要转换到区域2进行作图。由式(2)得：

对式(3)进行求导：

dy/dx=-(b2·x)/(a2y)

如果斜率大于-1(区域1)，则有：

b2x＜a2y

根据Bresenham算法的基本思想进行讨论，首先建立对称坐标系，把坐标原点定为椭圆中心点。设Pi-1点为已确定的逼近像素点，坐标为(xi-1,yi-1)，Pi-1点有两个靠近点Si点和Ti点，它们的坐标分别为：(xi-1+1,yi-1)、(xi-1+1,yi-1-1)。下面来分析讨论这两个点哪一个更靠近理论椭圆弧，然后选择更靠近的那个点作为椭圆弧的逼近像素点。设Si点和Ti点离椭圆弧的距离分别为D(Si)和D(Ti)，则有：

令di=D(Si)-D(Ti)，如果di≥0，则选择Ti点作为椭圆弧的逼近像素点；反之则选择Si点。

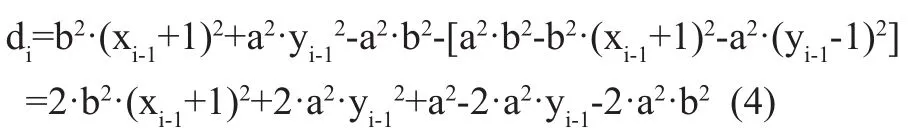
用i+1替代式(4)中的i，得：

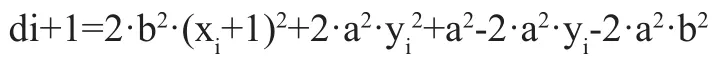
将di+1-di，即可得到：

若di≥0，则选择Ti点，此时有：

若di＜0，则选择Si点，此时有：

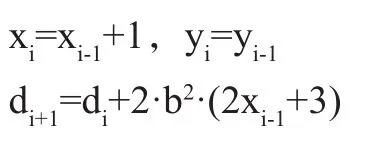
同理，将di的初始值为d1，代入式(4)得：

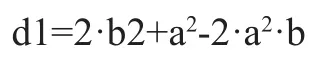
下面来讨论在区域2作图时的情况。如图3所示，设Pi-1点为已确定的逼近像素点，坐标为(xi-1,yi-1)，Pi-1点有两个靠近点Si点和Ti点，坐标分别为：(xi-1+1,yi-1)、(xi-1+1,yi-1-1)。同理，设Si点和Ti点离椭圆弧的距离分别为D(Si)和D(Ti)，则有：

图3 Bresenham算法构建椭圆弧(二)

D(Si)=b2·(xi-1+1)2+a2·(yi-1-1)2-a2·b2

D(Ti)=a2·b2-b2·xi-12-a2·(yi-1-1)2

根据式(2)同理可知，选择D(Si)和D(Ti)中更接近0的点即可。

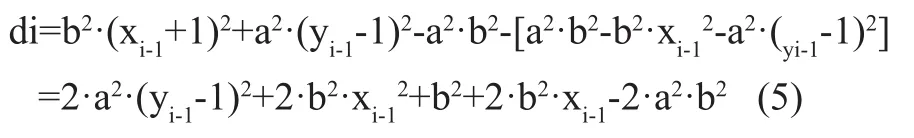
用i+1代替式(5)中的i，得：

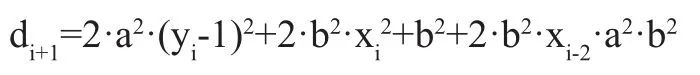
将di+1-di，可以得到：

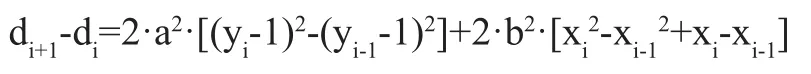
若di≥0，选择Ti点作为椭圆弧的逼近像素点：

若di＜0，选择Si点作为椭圆弧的逼近像素点：

三、结语

很多设计人员在LCD的GUI设计时面临着算法的选择，笔者也不例外，目前广泛被大家接受的算法主要有数值微分法(DDA)、中点画线法、Bresenham算法等，它们在不同图形设计时各具特色，这就需要设计人员根据自己的专长与需要进行选择。笔者在进行大量的实验的基础上认为Bresenham算法是一种具有高效性强、准确度高等特点的算法。上述分析有不到之处敬请指教。