具有年龄结构的手足口病模型的动力学分析

刘俊利, 刘白茹，吕 潘

(西安工程大学 理学院， 陕西 西安 710048)

0 引 言

手足口病是一种常见的儿童疾病，多发于5岁以下的儿童[1]，但任何人都可能感染该疾病。其中以柯萨奇病毒A16型(Cox A16)和肠道病毒71型(EV 71)最为常见[2-3]。该疾病通常情况下不严重，但是传染性极强，在学校和日托中心传播迅速。随着气候的变化，环球旅行的增加，病毒不断演化；由于一些国家缺乏卫生资源和有效的监测系统，预计未来手足口病爆发的频率也会增加。

手足口病是引起儿童死亡的主要原因之一，是一个严峻的公共卫生问题，还会造成社会和经济方面不可量化的问题。对于手足口病目前没有有效的疫苗和治疗措施，控制策略是采用适当的预防措施，其中包括隔离机制和个人保护防止接触感染者。因此，应用数学模型研究手足口病的传播十分重要。近年来，已有一些模型用于研究手足口病的传播。文献[4-6]建立了常微分方程模型，研究了平衡点的稳定性，分析了疾病的最优控制策略，这些模型被用于分析国内手足口病的传播。在许多国家手足口病呈现季节性的爆发[7-9]。文献[10-12]建立了周期传染病模型，从理论上分析了模型的动力学行为。然而，手足口病的严重程度是与年龄相关的，已有的数学模型忽略了手足口病的年龄依赖性。比如在中国台湾地区，每年重症病例变化显著，发病率随年龄增长而降低，1岁儿童发病率达到峰值[13]。考虑到手足口病与年龄有关的特点，本文研究了一类具有年龄结构的手足口病模型的动力学行为。

1 模型的建立

假设t表示时间，a表示人口的年龄，t时刻总人口的年龄分布记为N(t,a)，总人口分为易感染者、潜伏者、染病者、隔离者和恢复者等5个仓室，其年龄分布分别记为S(t,a)，E(t,a)，I(t,a)，Q(t,a)，R(t,a)。

设a+为人口的最大年龄，则感染力函数λ(t,a)为

(1)

具有年龄结构的手足口病模型由以下偏微分方程给出：

(2)

初值和边值条件如下：

总人口N(t,a)满足以下方程:

系统(2)中:β(a,σ)为染病年龄为σ的染病者接触并感染年龄为a的易感者的传染率；b(a)、μ(a)分别表示人口的出生率和死亡率；ω(a)为从潜伏者到染病者的转化率；δ(a)为染病者的隔离率；γ1(a)、γ2(a)分别表示染病者和隔离者的恢复率；α(a)为手足口病的因病死亡率。

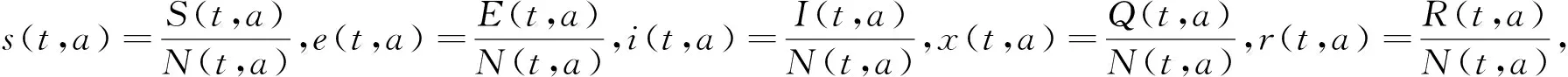
(3)

式中：

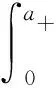
(4)

系统(3)的初值和边值条件分别为

s(t,0)=1

e(t,0)=i(t,0)=0

x(t,0)=r(t,0)=0

因为在系统(3)的前3个方程中x(t,a)和r(t,a)没有出现，因此可以研究如下系统

(5)

系统(5)的初值和边值条件分别为

s(t,0)=1,e(t,0)=i(t,0)=0

s(0,a)=s0(a),e(0,a)=e0(a),i(0,a)=i0(a)

系统(5)的状态空间为

Ω={(s,e,i)∈X+:0≤s+e+i≤1}

式中X+为X=L1(0,a+)×L1(0,a+)×L1(0,a+)的正锥。

假设A为线性算子，F:X→X为非线性算子，定义如下:

(Aφ)(a)=(A1,A2,A3)

式中：

A的定义域D(A)为

D(A)={φ∈X:φi∈AC[0,a+],

φ(0)=(1,0,0)T}

这里AC表示区间[0,a+]上的绝对连续函数的集合。

令u(t)=(s(t,·),e(t,·),i(t,·))T,则系统(5)可以表示成巴拿赫空间X上的半线性柯西问题

(6)

这里u0(a)=(s0(a),e0(a),i0(a))T。

根据文献[14]和文献[15]，得到如下结果:

引理1算子A产生C0半群exp(tA)。对于半群exp(tA)定义的半流状态空间Ω为正不变的。

引理2算子F在X上是Frechet连续可微的。

定理1∀u0∈X+，存在最大区间 [0,t0)。在区间[0,t0)上方程(6)存在唯一的弱解u(t,u0)∈X+，且

2 无病平衡点的稳定性

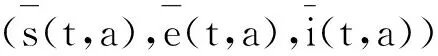
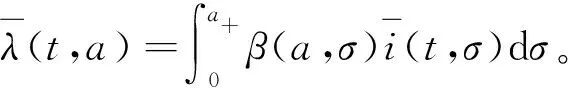
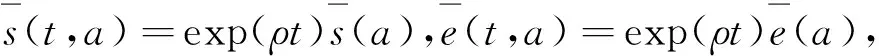
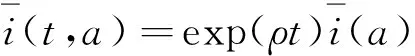
代入到式(7)中得

(8)

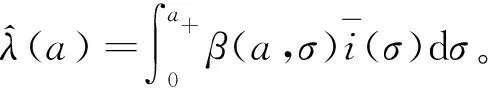
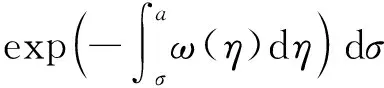
(9)

(10)

其中θ(a)=δ(a)+γ1(a)+α(a)。 把式(9)代入到式(10),得

(11)

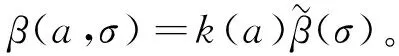
则得到如下特征方程:

(12)

根据文献[18]，定义系统(5)的基本再生数为R0=H(0)，即

(13)

关于无病平衡点P0(1,0,0)的局部稳定性，有如下结论:

定理2在假设1的条件下，当R0<1时P0(1,0,0)局部渐近稳定;当R0>1时P0(1,0,0)不稳定。

证明易知H(ρ)是连续、单调递减的函数，且

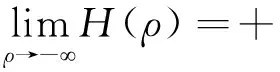
因此特征方程(12)有唯一的实根ρ*。若R0=H(0)>1，则ρ*>0，因此P0不稳定。

若R0=H(0)<1，则ρ*<0。令ρ=u+iv为方程(12)的任意根。因为Re(eρ)≤exp(Reρ),由方程(12)得

1=|H(u+iv)|≤H(u)

则Reρ=u≤ρ*<0，因此P0(1,0,0)局部渐近稳定。

事实上，手足口病引起的死亡率比较小。例如，根据山东省2009年4月到2011年10月的数据显示，因病死亡率为1.6×10-4。因此，给出另一个假设。

假设2假设手足口病的因病死亡率为零，即α=0。

在假设1和假设2的条件下，关于无病平衡点P0(1,0,0)，可以得到进一步的结论:

定理3如果假设1和假设2成立，则当R0<1时无病平衡点P0(1,0,0)全局渐近稳定。

L(t,a)≤k(a)V(t)

(14)

对系统(5)沿特征线积分,得

(15)

(16)

(17)

把式(16)代入式(17),得

(18)

由式(14)和式(18),得

(19)

令

对式(19)两边取上极限，由Fatou引理得

(20)

定义常数C为

(21)

式(20)可以表示为

W(a)≤k(a)C

则由式(21)得

CR0

因此,当R0<1时C=0，则

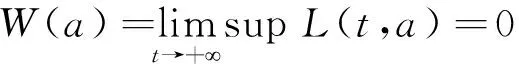
因此,由式(16)和式(18)得

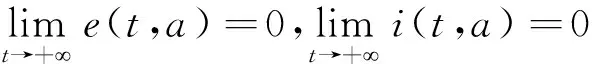
3 地方病平衡态的存在性与稳定性

定理4如果假设1和2成立,则当R0>1时，系统(5)存在唯一的地方病平衡态P*(s*(a),e*(a),i*(a));当R0≤1时，系统(5)不存在地方病平衡态。

证明令P*(s*(a),e*(a),i*(a))为地方病平衡态，则有

(22)

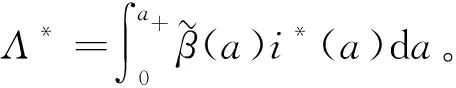
(23)

把式(23)代入到式(24)中,得

(26)

把式(26)代入到式(25)中,得

把i*(a)代入到Λ*的表达式中,得

即

(27)

把式(27)的右端记为G(Λ*)，则G(Λ*)是一个连续递减的函数且G(0)=R0。对于Λ*>0，当Λ*→∞时，

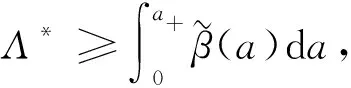
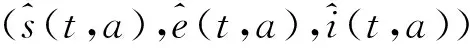
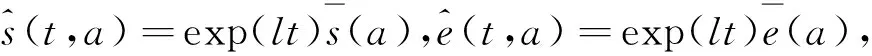
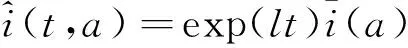
则得到如下线性系统：

(28)

初始条件为

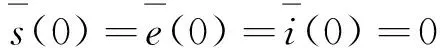
其中

(29)

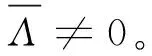
(30)

初始条件为s(0)=e(0)=i(0)=0。

由式(29)知，系统(30)的解满足以下方程

(31)

由式(30)知

把式(32)带入到式(33)中,得

(35)

把式(35)代入到式(34)得

则有

(36)

定理5如果假设1和假设2成立，则有以下结论:

1) 当l→+∞时，Θ(l)→0;

2)Θ(0)<1。

证明由式(36)知结论1)成立。令l=0，得

(37)

方程(27)意味着式(37)中的第一个积分等于1，因此Θ(0)<1。定理5得证。

因为

而且

则有

进一步可以得到

因此

假设∀0≤x≤η≤a≤a+，下面的不等式成立:

ω(y)dy≥0

(38)

定理6如果假设1，假设2和不等式(38)成立，则当R0>1时，系统(5)有唯一的地方病平衡态P*(s*(a),e*(a),i*(a))，且P*是局部渐近稳定的。

证明如果不等式(38)成立，则Θ(l)≥0且Θ(l)关于l是单调减少的。结合定理5知，Θ(l)=1有唯一的负实根。类似于对式(12)的讨论，可知Θ(l)=1所有的复根的实部都小于或等于这个唯一的实根。因此，P*是局部渐近稳定的。

4 结 语

手足口病是一种传染性极强的疾病，儿童和成年人均可以感染。手足口病的传播与宿主年龄有很大的关系。因此，为了使模型更加具有实际意义，本文在模型中考虑了宿主的年龄结构，分析得到了模型的基本再生数，讨论了无病平衡点的全局稳定性和地方病平衡态的局部稳定性。具有年龄结构的传染病模型的地方病平衡态的稳定性分析是一个困难的问题。在本文中仅仅给出了地方病平衡态局部稳定的充分条件，其全局稳定性的证明需要进一步研究。本文所得到的结果对手足口病的控制和预防具有一定的指导意义。