基于RF的Elastic Net-Logistic个人信用违约风险评估

陈 倩,贺兴时,杨新社

(1.西安工程大学 理学院,陕西 西安 710048；2.密德萨斯大学 科学与技术学院，英国 伦敦 NM4 4BT)

0 引 言

随着互联网金融的迅猛发展以及个人消费观念的快速转变,国内商业银行零售信贷业务，特别是个人信贷业务得到了发展，而个人信用风险是信贷业务面临的主要风险。如何尽可能地降低信贷损失,已成为金融机构的研究热点。我国的信用评估系统经过不断的发展已经相对成熟,但是仍然存在一定的拓展空间。如何选取合适的评价指标,进一步改善适合我国国情的个人信用评估系统,仍具有重大的现实意义。

现有的个人信用风险评估模型,大致可以分为统计分析方法、机器学习方法和统计分析与机器学习结合的组合模型方法[1-5]。包括多元线性回归[6]、判别分析[7]、Logistic回归[8]以及支持向量机、神经网络、决策树[9-12]等。其中,Logistic回归模型因为具有较强的变量解释能力,较高的预测准确率以及计算简单而被广泛用在风险评估领域[13]。然而,在实际个人信用风险模型中,影响风险的因素及需要解释的变量很多,传统的Logistic模型不能很好地解决多重共线性问题,导致计算了过多冗余变量而增加了模型复杂度[14],影响了模型的解释性和预测准确性[15]。针对这一缺陷,1996年,TIBSHIRANI提出了著名的Lasso方法,对模型的系数进行压缩,使得模型中绝对值较小的系数压缩至零[16]；2001年,FAN提出了惩罚似然函数方法,将Lasso惩罚(即L1惩罚)应用于广义线性模型,使其能够同时进行变量选择和系数估计[17]；2006年,KIM等提出对Logistic回归采用Group Lasso算法[18]。2015年,胡小宁等通过Lasso-Logistic回归模型研究了某银行的个人信贷数据,并与Logistic回归模型、基于逐步回归的Logistic模型进行比较分析。结果显示,在模型解释性和预测准确率方面前者都是最优的[19]。2016年,张婷婷等建立Adaptive Lasso-Logistic回归模型,并将其应用到个人信用风险评估问题,其结果比Lasso-Logistic模型和传统Logistic回归模型更具说服力[20]。同年,张碧月提出RF-APSOLSSVM二阶段个人信用评估模型,实证分析表明RF-Apsolssvm的预测精度比RF模型和Apsolssvm模型的精度高[21]。2017年,余华银等运用决策树和Logistic回归对网贷平台进行实证分析,结果表明2个模型都具有较好的分类能力,其中决策树表现最优[22]。2020年,邓丽纯等运用Cox模型预测上市公司财务危机,结果表明Cox比例风险模型不但能够解决空值信息,还能预估数据在指定时刻的生存率状况[23]。

目前,在个人信用评估领域中构建的模型是以提高模型精度为主要目的,并逐渐从单一模型转向组合模型; 而将统计分析与机器学习相结合的组合模型兼顾预测精度、稳健性和解释性,在个人信用风险评估领域越发受学者的关注。本文通过模拟实验，建立了基于随机森林[24](random forest,RF)的弹性网[25](Elastic Net)- Logistic个人信用违约风险评估模型及基于RF的Lasso-Logistic模型,并进行比较分析。

1 风险评估的模型

1.1 弹性网模型

文献[25]提出了Elastic Net方法，其估计为

βenet=arg min{‖y-Xβ‖2+

λ2‖β‖2+λ1‖β‖1}

(1)

式中：λ1和λ2是非负参数；y=(y1,y2,…,yN)T为N维因变量；β=(β1,β2,…，βp)T为Logistic回归系数；X为N×p阶矩阵。该方法是L1惩罚和L2惩罚的结合,惩罚的L1部分生成一个稀疏模型,惩罚的L2部分能够连续收缩,在一定程度上消除了变量之间的多重共线性。当变量之间强相关时,弹性网方法能够有效处理,将必需的强相关变量组全部选入模型,而不会只选择其中一个变量。

βenet=arg min{‖y-Xβ‖2+

λ[α‖β‖2+(1-α)‖β‖1]}

(2)

式中：λ为非负参数；α∈[0,1]是一个可变参数。当α=1时,弹性网方法变为岭回归; 当α=0时,弹性网方法变为Lasso方法。当0<α<1时,弹性网方法既可以简化模型,增加模型的预测精度，还尽可能保留重要的解释变量,不影响模型的解释力。

1.2 基于RF的Elastic Net-Logistic模型

通过分析,弹性网只有当特征变量之间存在高相关性时,预测精度才会显著提高。RF算法对于不平衡的数据集可以平衡误差,对具有部分特征遗失的数据集可以填补缺失值,并且可以有效避免过度拟合,适用的样本类型更广泛。所以，本文首先采用RF算法进行变量筛选,给出解释变量重要性的度量,剔除不重要的变量；其次，利用整理好的变量拟合Elastic Net-Logistic回归模型及Lasso-Logistic回归模型；最后,建立有关个人信用违约风险评估的预测模型。

假设有n个独立同分布的客户信用样本观测值(xi,yi),xi为第i个客户的观测值,yi为响应变量,yi∈{0,1},0代表“坏”客户,1代表“好”客户。

假设πi=P(yi=0|xi)是将客户i评判为“坏”的概率,对πi做Logit变换,记为Logit(πi),即

(3)

式中:β0为截距；xi=(xi1,xi2,…,xip)T为p维协变量。

对式(3)取最大似然函数,得

(4)

则回归参数的估计就是将式(4)最大化,即

maxL(β)

(5)

于是得到Logistic回归模型下的Elastic Net方法的定义,即

(1-yi)ln(1-πi))]+

(6)

(1-yi)ln(1-πi))]+

(7)

式(7)分为2个部分:第1部分

表示模型的拟合程度;

第2部分

表示对进入模型的变量的惩罚力度,最终选出的变量集合要使这2部分的值达到最小。当α=0时,式(7)变为Lasso-Logistic回归模型。

2 风险评估模型应用实例

2.1 数据描述

使用来自加州大学欧文分校(UCI)机器学习数据集仓库公开的南德信贷数据(2020年)。该数据集共有1 000个观测记录和21个变量。其中前20个变量是对贷款申请人的个人特征描述,最后1个变量(yi)是该银行对客户信用等级的评判:0为“坏”客户,1为“好”客户。个人特征属性包含了有关客户的20项指标,分别是现有支票状况(xi1)、贷款期限(xi2)、历史信用记录(xi3)、贷款用途(xi4)、信贷额度(xi5)、储蓄账户/债券状况(xi6)、工作年限(xi7)、分期付款占可支配收入百分比(xi8)、性别/婚姻(xi9)、担保情况(xi10)、居住年限(xi11)、个人资产(xi12)、年龄(xi13)、其他分期付款计划(xi14)、住房情况(xi15)、此银行已有贷款项目数(xi16)、工作性质(xi17)、供养人数(xi18)、是否有电话(xi19)、是否外籍雇工(xi20)。在这1 000条个人信贷记录里,被定义为“好”客户的有700人,另外300人被定义为“坏”客户。

2.2 数据预处理

结合现有信用指标选取资料[26],对数据指标进行初步筛选。其中贷款用途(xi4)属性取值多达10个,但是其样本分布极其不均匀,并且某些属性对应样本数不足1%,违反了信用评估指标体系构建的层次性原则和可操作原则,因此删除。性别/婚姻(xi9)原本应是2个评价指标,在该数据集中将二者合为1个指标,违反了信用评估指标体系构建的科学性原则,因此删除。

删除这2个比较明显有问题的指标后,再对剩余的18个指标进一步筛选,其中共有8个属性变量和10个数值型变量。将8个属性变量进行哑编码。以是否有电话(xi19)为例:“否”标记为0,“是”标记为1。若属性变量的种类超过1个,以住房情况(xi15)为例:“免费住房(xi15_0)”标记为(1,0,0),“租房(xi15_1)”标记为(0,1,0),“自有住房(xi15_2)”标记为(0,0,1)。变换之后的变量由原本的8维扩充到24维。10个数值型变量中,有3个变量(xi2,xi5,xi13)为一般意义下的连续取值,为消除数据量纲影响,将这3个连续型数值变量进行“z-score”标准化。剩下的7个变量实际取值为离散值,且取值具有大小的意义,因此可看成有序变量,按照变量影响由小到大的顺序编码为1、2、3、4、5。处理后解释变量共34个,即p=34,因变量1个。

确定训练集与测试集分割比例为7∶3,即对整个数据集随机抽取70%作为训练集,30%作为测试集。

2.3 模型比较及结果分析

将处理好的数据集应用RF算法对解释变量进行重要性度量(见表1),筛选重要变量。对于RF算法的参数,通过计算基于OOB数据的模型误判率均值,选取最小误判率mtry=6。另一个重要参数节点数ntree通过运行结果选取，ntree=310。本文提出的模型运算均通过R语言编辑。

表 1 随机森林对各个变量的重要性度量Tab.1 The importance measure of random forests to individual variables

表1为RF算法对各个变量的重要性度量表,包含2种度量方式:第1种度量方式是精度平均减少值; 第2种方式是节点不纯度平均减少值。在输出的结果中,对应变量的重要值越大,说明该变量对于模型进行分类越重要。根据显著性删除xi18、xi19、xi20、xi12_1、xi12_2、xi17_0、xi17_2等7个变量,还剩27个解释变量。

用RF算法筛选出来的27个解释变量构建基于RF的Lasso-Logistic模型和基于RF的Elastic Net-Logistic模型,并用初始的34个解释变量构建全变量Elastic Net-Logistic模型。3个模型分别用于个人信用违约风险评估。以预处理过程中随机选取的70%的观测值作为训练样本,剩下的30%作为预测样本,以BIC作为准则进行变量选择和比较。将预测结果与原有数据的客户标签变量,即顾客“好”与“坏”的分类结果逐一比较,结果见表2和表3。

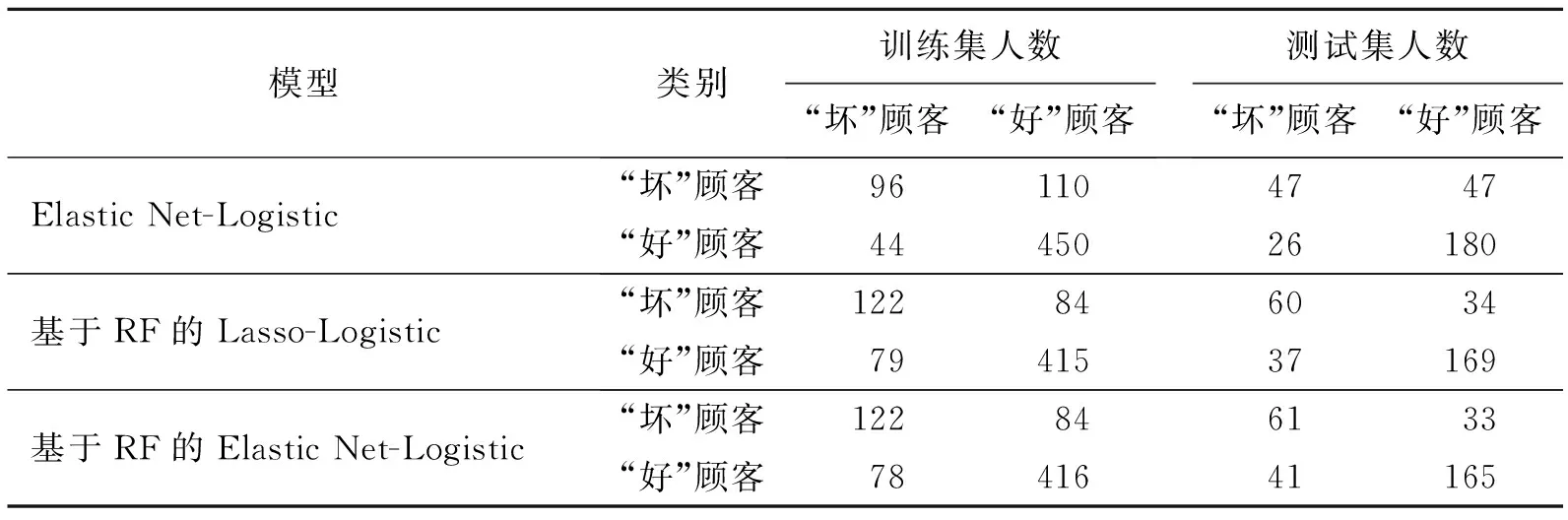
表 2 3个模型对样本顾客的分类预测结果Tab.2 Classification prediction results of customer samples by three models

表 3 3个模型对样本比例的分类预测结果

建立个人信用违约风险模型的主要目的是为了正确判定违约客户和不违约客户。若将违约客户判定为不违约客户,对放贷机构而言损失更大,潜在风险也更大。因此,本文着重关注模型的违约召回率,即违约客户被正确预测的概率,其次关注模型的精度(整体客户被正确预测的概率)与不违约召回率(不违约客户被正确预测的概率)。

从表2和表3可以看出:首先,基于RF的Elastic Net-Logistic模型与Elastic Net-Logistic模型相比,前者违约召回率与精度更高,不违约召回率相对偏低,但都保持在80%以上; 其次,基于RF的Elastic Net-Logistic模型和基于RF的Lasso-Logistic模型相比,虽然2个模型在训练集中的违约召回率一样,但前者精度更高。在测试集中,基于RF的Elastic Net-Logistic模型的违约召回率和精度均高于基于RF的Lasso-Logistic模型。整体来看,基于RF的Elastic Net-Logistic模型和基于RF的Lasso-Logistic模型从训练集到测试集违约召回率与精度都在提高,而传统的Elastic Net-Logistic模型从训练集到测试集精度在下降,即加入RF算法后的模型性能更好。比较而言,基于RF的Elastic Net-Logistic方法建立的个人信用违约风险评估模型更具有优势。

2.4 实例应用

为降低实验结果偶然性,进一步验证本文模型的有效性,选取加州大学欧文分校(UCI)机器学习数据集仓库提供的澳大利亚信贷数据进行实例验证。该数据集共有690条观测记录,15个属性变量。与南德信贷数据相似,前14个变量是对贷款申请人的个人特征描述,其中有6个属性值为连续值,8个属性值为离散值。最后1个类变量是该银行对客户信用等级的评判:第一类为“坏”客户,共383个; 第二类为“好”客户,共307个。采用相同的数据预处理方法及训练集、测试集分割比例进行实验,各模型在测试集上对样本的预测结果如表4所示。

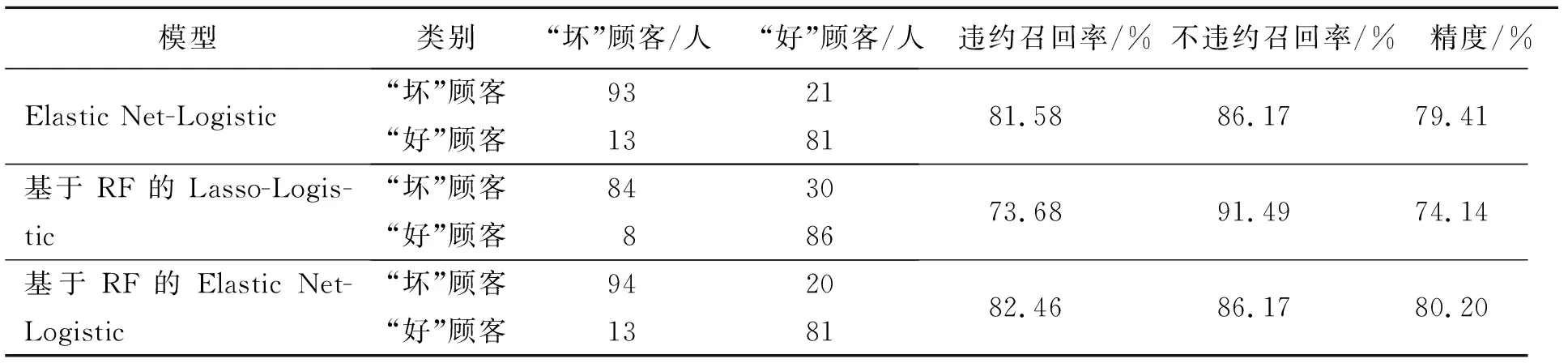
表 4 模型对样本的分类效果Tab.4 Comparison of models classification effect

从表4可以看出：基于RF的Elastic Net-Logistic模型在违约召回率上比传统的Elastic Net-Logistic模型和基于RF的Lasso-Logistic模型分别提高了0.88%和8.78%; 在分类精度上分别提高了0.79%和6.06%; 不违约召回率均保持在86%以上。可见,基于RF的Elastic Net-Logistic模型更适用于个人信用违约风险评估问题。

3 结 语

本文引入基于RF的Elastic Net-Logistic方法建立个人信用违约风险评估模型,对南德信贷数据与澳大利亚信贷数据进行实证分析,并与传统的Elastic Net-Logistic方法和基于RF的Lasso-Logistic方法进行对比分析。结果表明:3个模型均有一定的稳定性,但是从分类与预测准确性看,基于RF的Elastic Net-Logistic方法较其他2种方法有明显的优势。该方法有更高的违约召回率,即违约客户被正确预测的概率更高,能减少放贷机构的坏账率,更加符合个人信用违约风险评估的要求。可见,基于RF的Elastic Net-Logistic的个人信用违约风险评估模型，能够为银行及其他金融机构在评判客户信用违约风险中起到一定的指导作用。

本文提出的模型可以处理不平衡数据集，并且适用于特征变量存在高度相关性的情况。在实际问题中,可以将贷款申请人的个人特征作为输入变量，利用该模型预测客户风险状况,及时预防和避免违约状况的发生。但是,本文只考虑了把客户分为“好”“坏”等2种类别,而在实际情况中,可能需要将客户分为更多的类别；同时,由于相关信息的保密性,数据来源受到限制。因而，本文采用的信贷数据集的数据量并不大,不能全面反映目前复杂的个人信贷消费场景，有待根据具体情况进一步完善。