计及日特性和季特性的风矢量仿真模型及应用

李 晗 邹建华 张远航 杨保华

(三峡大学 电气与新能源学院，湖北 宜昌 443002)

风能是一种清洁的可再生能源，发电成本低且储量巨大，因此风电规模在我国及全球范围内发展迅速.2015年，我国新增风电装机容量30.5 GW[1]，总容量和发电量分别达到145.1 GW和1.863×105GW·h[2].截至2021年2月，我国风电装机总容量达到284.56 GW，其中2021年1～2月新增装机容量达到3.57 GW[3].风速的随机性和间歇性使得风力发电具有波动性和不可控性，随着风电渗透率的升高，风电并网可能对电网的可靠性产生影响.研究含风能电力系统充裕度评估方法，评估风能对电力系统的可靠性效益，可以为电力系统运行与规划提供帮助.

准确的风速模型是模拟风电场出力的重要条件，常用风速模型可分为概率分布模型和时间序列模型两类.概率分布模型能够较好地刻画风速的分布特性[4-6]，但难以描述风速随时间动态变化的特性；时间序列模型大多可分为两类：一种基于回归分析模型[7-9]，一种基于马尔科夫链模型[10-11].风速具有复杂特征，既有一定的周期性，又同时随季节更替而变化.为研究风速的日周期性，文献[11]按时序将历史风速数据分为24组数据集，分别建立24个马尔科夫链模型，并且提出季节系数以描述风速的季节特性.除日周期特性外，风矢量也有一定的月周期特性，文献[12]使用傅里叶变换将三角函数与国内多个地区历史风速数据进行拟合，结果表明该地区风速具有明显的月周期特性.当前多数模型专注于研究风速随机性，较少刻画风向随机性，而风向是刻画风电场尾流效应的重要变量.尾流效应对风电机组出力有显著影响，导致风电机组发电量损失可达10%～15%[13].因此单一的风速模型难以计及尾流效应影响，进而导致对风电机组出力的乐观预测.另一方面，风速和风向具有一定的季特性，文献[14-15]分别统计国内和国外多个地区的历史风速数据，结果显示风速均值在不同季节存在较大差异.目前大多数风速模型并未考虑季特性，可能导致充裕度评估误差.

为考虑尾流效应和风矢量的季特性，本文将风速和风向定义为风矢量，提出计及日特性和季特性的风矢量仿真模型.该模型的建模过程主要分为两步：第一步，将实测数据分为24组数据集，分别建立马尔科夫链模型得到计及日特性的风矢量模型，其中为划分二维风矢量的马尔科夫状态空间，提出一种基于正交分解准则的聚类算法；第二步，引入最优季度系数，逐季度修正第一步得到的风矢量样本，使其具有季节特性.另一方面，本文将提出的风矢量仿真模型与Jensen尾流模型和时序蒙特卡罗模拟法结合，提出计及日特性和季特性的含风能发电系统充裕度评估方法，分析风机布局和峰值负荷对系统充裕度的影响.

1 风矢量定义及其日特性和季特性

本文将风速和风向定义为二维笛卡尔坐标系中的方向性矢量：风矢量w=(v，θ)，如图1所示.其中v为风速，表示风矢量长度；θ表示风向，为风矢量与x轴的夹角.定义正东方向为0°，并与x轴正方向重合，则当风矢量沿逆时针方向偏离x轴时，风向从0°增大至360°.此外，vx和vy分别为风矢量在x轴和y轴的分量.

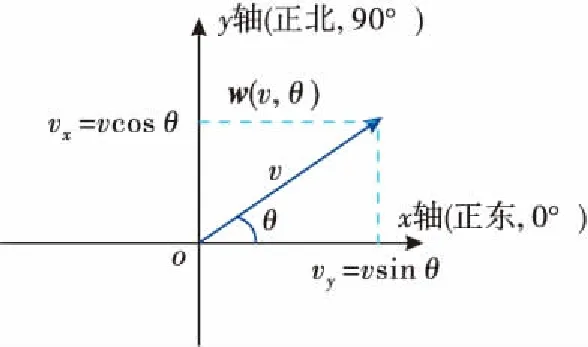
图1 风矢量示意图

为说明风矢量的日特性和季特性，通过访问开放气象数据库North Dakota Agricultural Weather Network(NDAWN)[16]，得到美国North Dakota州Berthold观测站2006年至2010年间的实测每小时风矢量数据.图2所示为24 h风速和风向均值与标准差.可以看到，在下午时段风速均值较大，同时风速和风向的波动性略高于平均水平.这表明由风速和风向组成的风矢量具有明显的日特性，应以24 h为周期，研究风矢量的日特性.

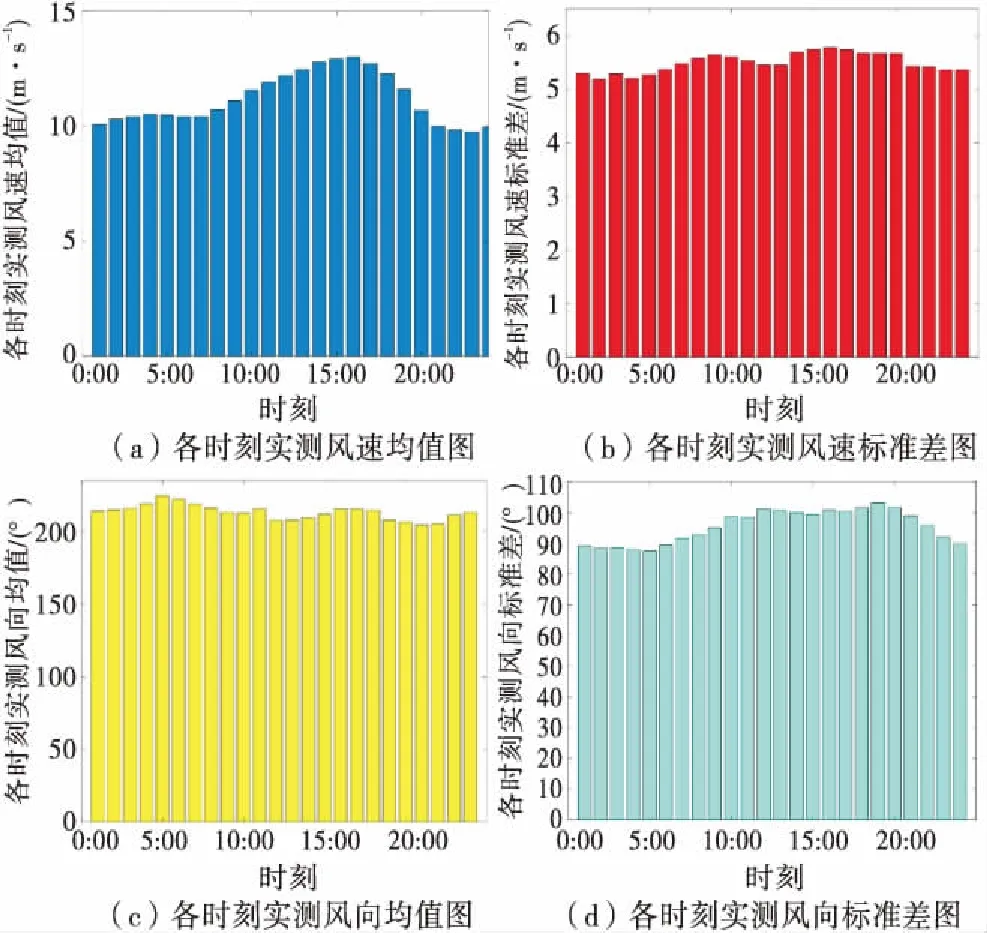
图2 各时刻实测风矢量柱状图

图3为2006年至2010年间各季节实测风矢量均值和标准差.可以看到，在相同年份，四季风速风向均值和标准差不尽相同；在不同年份，同一季节的风速风向均值和标准差也存在差异.总的来说，风速的均值和标准差在春季和冬季较高，在夏季和秋季较低；风向的均值在秋季和冬季较高，标准差在春季最高.所以，由风速和风向组成的风矢量的季特性，体现在各季的风速风向均值和标准差随着季度和年份的更替而波动变化.

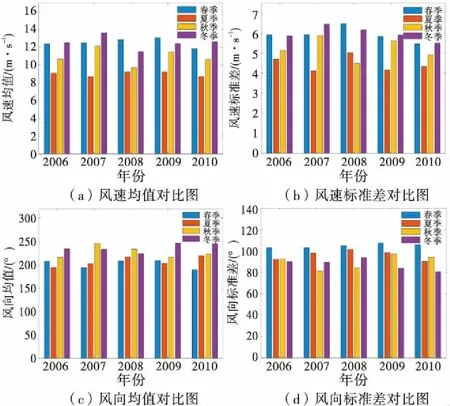
图3 各季节实测风矢量对比图

2 计及日特性和季特性的风矢量仿真模型

2.1 计及日特性的风矢量马尔科夫链模型

将每天同一时刻的历史风矢量数据划分至同组集合，则可得到24组风矢量数据集.以该24组风矢量数据集，建立24个马尔科夫链模型，进而抽样产生计及日特性的风矢量仿真样本，以下为详细建模过程.建立马尔科夫模型，首先要将风矢量划分为多个马尔科夫状态空间.由于风矢量中的风向为圆周变量，对风矢量状态划分造成困难，故本文采用正交分解方法将风矢量转换为图1二维笛卡尔坐标系中的x、y轴线性分量vx和vy，而后通过聚类算法进行风矢量状态的比较和划分.

以第1小时为例，该小时的风速马尔科夫链的建模步骤如下：

步骤1：将第一时刻所有风矢量数据转换为x，y分量形式：vx=vcosθ，vy=vsinθ；

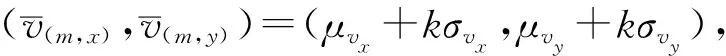
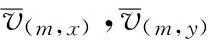
(1)

步骤4：应用每组风矢量聚类中的风矢量x轴和y轴分量的均值更新该组风矢量聚类中心，进而得到5组更新后的风矢量聚类中心；

步骤5：重复步骤3和4，不断更新风矢量聚类中心，直到当前聚类中心与前一聚类中心的欧式距离低于δ(δ=0.001)为止，得到第1小时中5组风矢量聚类中心和各聚类中的风矢量数据.

其他时刻的风矢量数据聚类算法和第1时刻相同，至此完成对一天24个时刻的风矢量聚类划分.

根据上述步骤的划分结果，可将每时刻风矢量均划分为5组聚类空间.对每时刻的风矢量建立马尔科夫链模型，以每组聚类空间作为马尔科夫状态空间，建立每个时刻的风矢量所属聚类空间的转移率矩阵，见式(2)：

(2)

式中，转移率矩阵G的每个元素表示一种转移关系，行数和列数分别表示转移前后的状态.例如，λ[1，1]和λ[1，5]分别表示风矢量状态S1向自身转移的转移率和向状态S5转移的转移率.

根据马尔科夫链方法，转移概率的表达式如下：

(3)

式中：fi，j为风矢量从第i个状态转移到第j个状态的转移次数；K为总状态数.

根据前面的每时刻风矢量聚类状态划分结果，需对每个风矢量聚类状态建立联合概率分布模型，以抽样每个马尔科夫状态空间的风矢量具体数值.本文应用copula方法建立风速与风向的联合概率分布，以此表示风矢量概率分布.根据copula方法，风矢量的概率密度函数可表示为[17]：

f(v，θ)=c(F1(v)，F2(θ))f1(v)f2(θ)

(4)

式中：c(v，θ)为copula概率密度函数；f1(v)和f2(θ)分别为风速和风向边缘概率密度函数；F1(v)和F2(θ)分别为风速和风向边缘累积概率密度函数.copula函数种类较多，具体copula函数类型的选择过程在4.1节中叙述.

本文选择风速模型中应用最为广泛的Weibull模型为风速变量的边缘概率分布模型.Weibull分布的概率密度分布和累积概率分布参见文献[18].

采用Von Mises模型为风向的边缘概率分布模型，Von Mises模型可描述随机变量的多峰分布特征，其分布模型参见文献[19].

风速和风向边缘分布中的参数均通过最大似然估计法求出.至此，建立风矢量马尔科夫链模型和每个马尔科夫状态内的风速风向联合分布模型.通过先抽样马尔科夫状态空间序列，再抽样风速风向的累积分布值，最后逆抽样得到风速风向的具体数值，流程如图4所示.

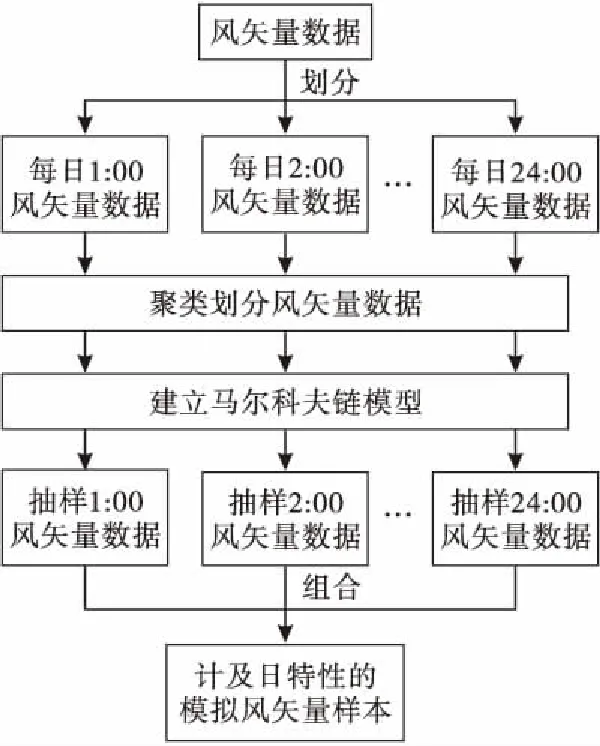
图4 计及日特性的风矢量模型建立和抽样流程图

2.2 计及季特性的最优季度系数

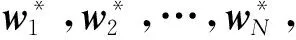
w+=(ωvv*，ωθθ*)

(5)

式中：ωv为风速修正系数；ωθ为风向修正系数；w+为修正后的风矢量；v*和θ*为计及日特性的风速样本和风向样本.

以风速修正为例，根据样本均值和标准差计算公式，可知修正前后风速均值和标准差满足以下条件：

(6)

(7)

根据式(6)和(7)，修正后风速数据的第t年第j季度的均值和标准差与实测风速均值和标准差的偏差可表示为以下偏差函数：

(8)

式中：ωv，μ和ωv，σ为风速的均值和标准差在偏差函数中的权重系数，可根据工程人员的实际需要进行设定和调整.该式表明，修正风速的各季度的风速均值和标准差与实测风速均值和标准差间的偏差可表示为关于修正系数ωv的非线性函数.

对式(8)中偏差函数fv(ωv)求取关于修正系数ωv的偏导函数hv(ωv)，其表达式如下：

(9)

根据经典优化算法可知，当选取最优修正系数ωv使式(9)中偏导数为零，可使得式(8)偏差函数达到最小值.即令式(9)为零，可得到最优修正系数的表达式如下：

(10)

类似地，可推导得到第t年第j季度风向修正系数为：

(11)

式中：ωθ，μ和ωθ，σ分别为风向的均值和标准差在风向修正过程中的权重系数.

图5为引入风矢量季特性的流程图，根据式(10)和(11)，由每季度计及日特性的模拟风速样本和实测风速样本的均值和标准差，可计算得到每季度的最优季度系数，并使用该系数使修正后的风矢量具备季特性.

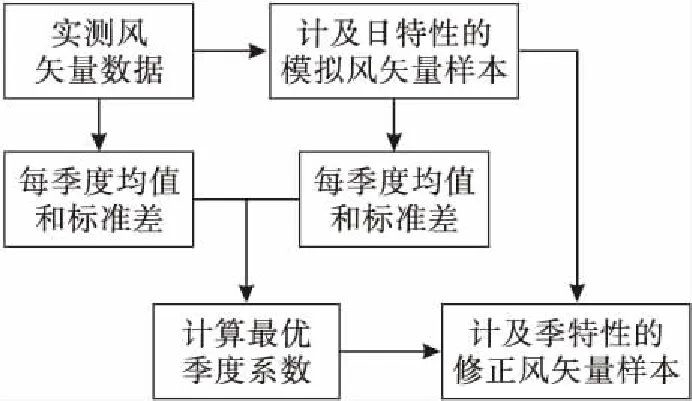
图5 风矢量季特性引入流程图

2.3 计及日特性和季特性的风矢量仿真算法

根据2.1节和2.2节内容，可给出计及日特性和季特性的风矢量仿真算法，以一个季度的抽样过程为例，其详细步骤如下.

步骤1：按照时刻划分，分别抽样24个马尔科夫状态空间序列；

步骤2：根据copula模型，抽样每个马尔科夫状态空间的风速和风向累积概率分布值，使用逆抽样法得到计及日特性的风速和风向样本；

步骤3：计算最优季度系数，得到计及日特性和季特性的仿真样本.

以上是一个季度的风矢量抽样过程，改变年份和季度，可得到更多的修正风矢量仿真样本.由于统计样本有限，当仿真年限超过实测样本长度时，将实测样本重置为第一年，进行循环抽样.

3 计及日特性和季特性含风能电力系统充裕度评估方法

3.1 发电机组两状态运行模型

为验证计及风矢量日特性和季特性的风矢量仿真模型，拟将风电场并入IEEE-RTS79节点系统，使用时序蒙特卡罗法计算系统的充裕度指标.其中发电机停运模型为两状态马尔科夫模型，通过“运行-停运-运行”的循环过程来模拟发电机的运行状态[20].

图6为发电机状态转移图，其中λ和μ分别为机组的失效率和修复率，根据λ和μ可循环抽样每台机组的运行时间TF和修复时间TR，来模拟发电机的运行状态.

图6 发电机状态转移图

(12)

(13)

式中：U和U′为(0，1)之间的均匀分布随机数.

3.2 计及日特性和季特性的含风能发电系统充裕度评估流程

本文将风矢量仿真模型与时序蒙特卡罗模拟法结合，提出计及日特性和季特性含风能电力系统充裕度评估方法，使用缺电不足期望ELOE和缺电时间期望ELOL描述系统充裕度水平，详细步骤如下.

步骤1：根据2.3节的方法得到计及日特性和季特性的修正风矢量仿真样本；

步骤2：根据公式(12)和(13)抽样得到每台机组的运行状态曲线.常规机组处于运行状态时，其输出功率为额定功率，风电机组的功率计算按照Jensen尾流模型[21]进行计算，当风机流入风速为vw时，其输出功率为：

(14)

式中：vci、vr和vco分别为风机切入风速、额定风速和切出风速，查询机组运行参数可知.a、b和c为恒定值，可由vci、vr和vco计算得到[21].

步骤3：将所有机组的输出功率相加，得到含风电系统的发电功率曲线；

步骤4：逐小时比较发电功率曲线和负荷曲线，得到每小时缺电量ENS曲线和缺电持续时间TLD曲线；

步骤5：根据ENS和TLD计算系统充裕度指标ELOE和ELOL.

(15)

(16)

为确保仿真结果的准确性，以ELOE的方差系数作为收敛条件，当其方差系数小于0.05或仿真年限达到8 000年时结束仿真.

按照以上步骤可计算得到系统的充裕度指标，应用于具体算例中.

4 算例分析

4.1 计及日特性和季特性的风矢量仿真模型验证

本文从NDAWN网站收集到美国North Dakota州Berthold观测站2006年至2010年间的风矢量数据[16].应用本文收集到的Berthold观测站的实测风矢量数据验证本文模型，结合2.1节和2.2节的模型参数，采用最大似然估计法，分别计算Gaussian copula函数、Gumbel copula函数、Frank copula函数和Clayton copula函数的未知参数，抽样得到计及日特性的模拟风矢量仿真样本和计及日特性和季特性的修正风矢量仿真样本.将仿真风矢量样本与实测风矢量样本的均值进行比较，见表1.

根据表1中的的对比结果，发现应用Gumbel copula函数后，可使得仿真风矢样本的均值最接近实测风矢量样本的均值，故选取Gumbel copula函数为风速和风向的联合概率分布模型.

表1 不同copula函数类型的仿真风矢量样本与实测风矢量样本的均值对照表

由于数据分类较多，以时刻1：00的风矢量模型为例，该数据集的风矢量分为5个聚类空间，聚类空间之间的转移概率见表2，每个聚类空间内风矢量的分布参数见表3.

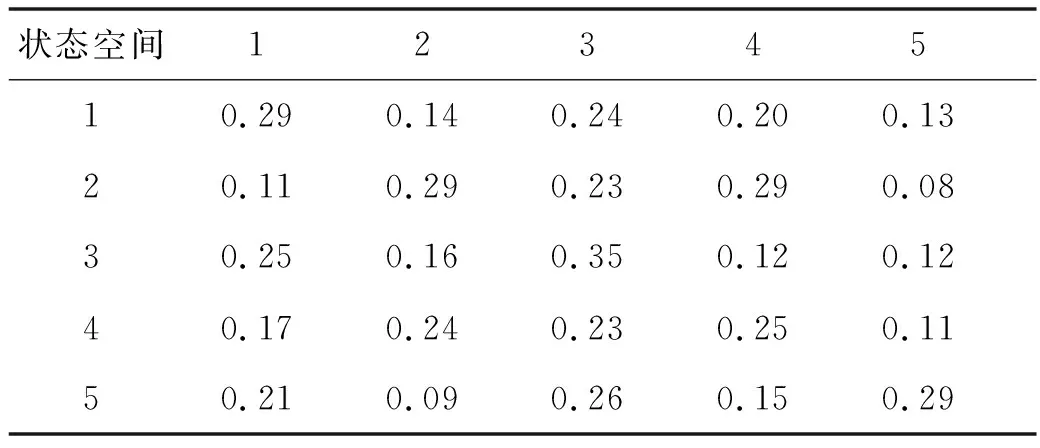
表2 马尔科夫转移概率表

表3 模型参数表

本文以ARMA(自回归滑动平均模型)[22]和一阶马尔科夫链模型[23]作为对照以验证模型的日特性，由于数据分类较多，选取其中6个时刻的数据对比见表4和表5.

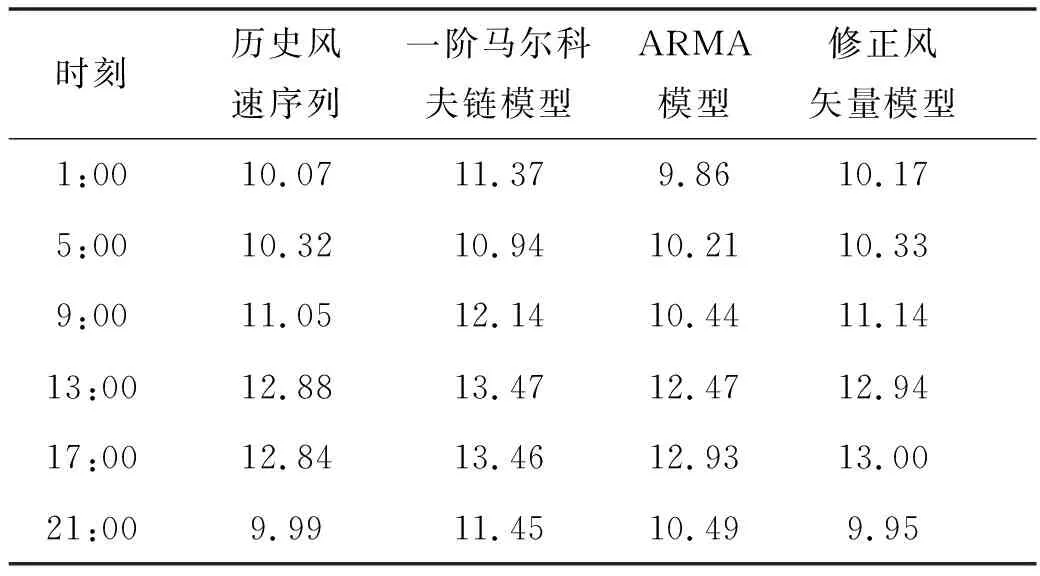
表4 不同风速时间序列的平均值比较(单位：m·s-1)

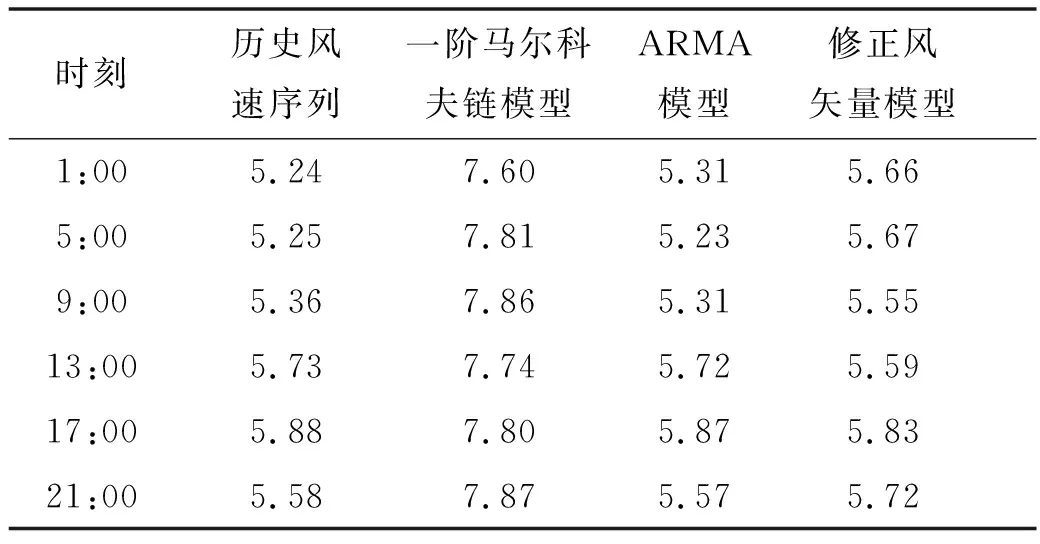
表5 不同风速时间序列的标准差比较(单位：m·s-1)

通过表4和表5可以看出，本文提出的计及日特性和季特性的风矢量修正模型在各时刻风速均值方面与历史风速序列最为接近，在各时刻标准差方面较为接近，体现了风矢量的日特性.

以一年4个季度的模拟风矢量和仿真风矢量为样本，前者仅计及风矢量的日特性，后者计及风矢量的日特性和季特性.将这两组风矢量与实测数据进行对比，当公式(10)和公式(11)的权重系数均取值为0.5时，修正前后的风速数据对比如图7所示.图7中蓝色数据为实测风矢量，棕色数据为只计及日特性的模拟风矢量，黄色数据为计及日特性和季特性的修正风矢量.通过表1可以看出，仅计及日特性的模拟风矢量数据的全年均值与历史风矢量数据很接近.但观察图7可发现，模拟风矢量的每季度数据与实测数据存在一定差异，并不具备季节特征.当风速风向各自的均值和标准差权重系数均取0.5时，修正系数对每季度风速和风向均值的修正效果较为明显，对风向标准差的修正效果较小.结果表明，最优季度修正系数的引入，使风矢量模型具备一定的季特性.

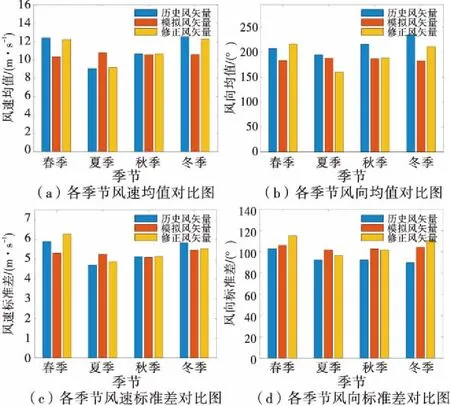
图7 不同风矢量各季度对比图

4.2 日特性和季特性对系统充裕度的影响

为评估季特性对系统充裕度的影响，本文假设North Dakota州Berthold观测站的某座风电场由100台相同型号风电机组组成，且该风电场接入IEEE-RTS79发电系统，该系统由32台常规机组组成，总装机容量3 405 MW，峰值负荷为2 850 MW，系统具体参数参见文献[24].风电场内100台风电机组按照10行10列的方式均匀布置，且相邻风电机组间的间距取值12r，其中r为风电机组叶轮半径40 m.风力发电机的额定功率为2 MW，其切入、额定和切出风速分别为3、12和25 m/s，风机的故障率和修复率分别为0.02和0.002 2.

风电场接入前，原始IEEE-RTS系统的ELOL和ELOE分别为9.37 h/a和1 197.4 MW·h/a.应用本文3.3节充裕度评估流程，评估以上含风能IEEE-RTS发电系统充裕度.为进行对比，本文也使用一阶马尔科夫链模型和ARMA模型作为风速仿真模型，评估该风能IEEE-RTS发电系统充裕度.三者对比结果见表6.

表6 不同风矢量模型对应的系统充裕度指标

可以看到：风电场接入后，系统的ELOL和ELOE指标均降低，表明风电接入对系统充裕度具有有益贡献；如忽略风矢量季特性和尾流效应，将导致充裕度结果评估过于乐观.在模型中加入风矢量的季特性，将对结果产生一定影响.

4.3 尾流效应对系统充裕度的影响

为评估尾流效应对系统充裕度的影响，本文选取4种风电场布局情形，每种情形下的风电场仍按照10行10列的方式均匀布置，但相邻风电机组间距分别取值5r，10r，12r和15r.应用本文充裕度评估方法，评估不同布局情形下的系统充裕度结果见表7.

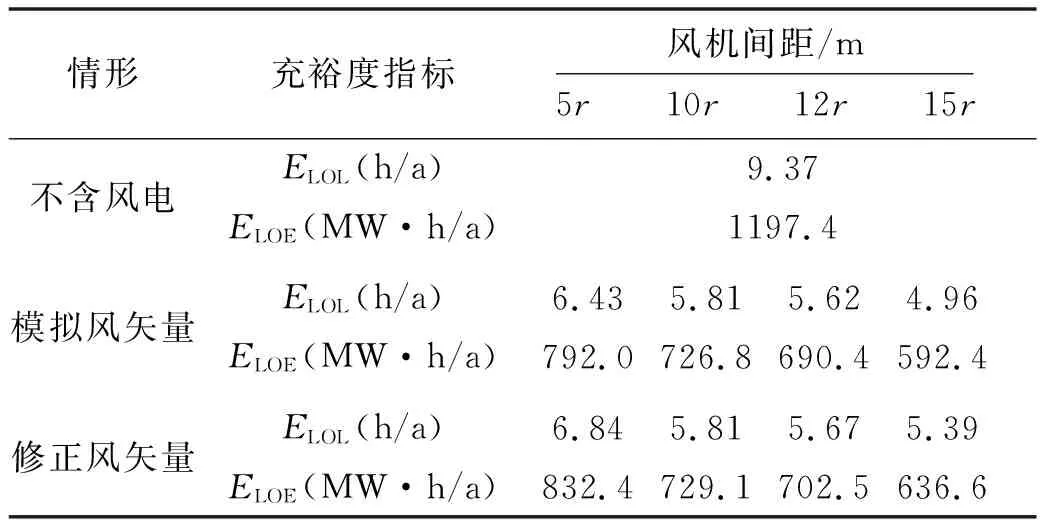
表7 不同风机间距下的系统充裕度指标

可以看到：风机间的尾流效应对系统充裕度有负面影响，且风机间距越小，尾流效应越强，对系统的充裕度影响越大.在不同风机间距条件下，应用修正风矢量进行系统充裕度评估得到的指标均低于模拟风矢量.结果表明在不同尾流条件下，忽略风矢量的季特性均可能导致过于乐观的充裕度评估结果.

4.4 峰值负荷对系统充裕度的影响

以2 850 MW作为系统峰值负荷的基准情形，改变峰值负荷分别取2 750、2 950和3 050 MW，不同峰值负荷参数下的系统充裕度指标见表8.

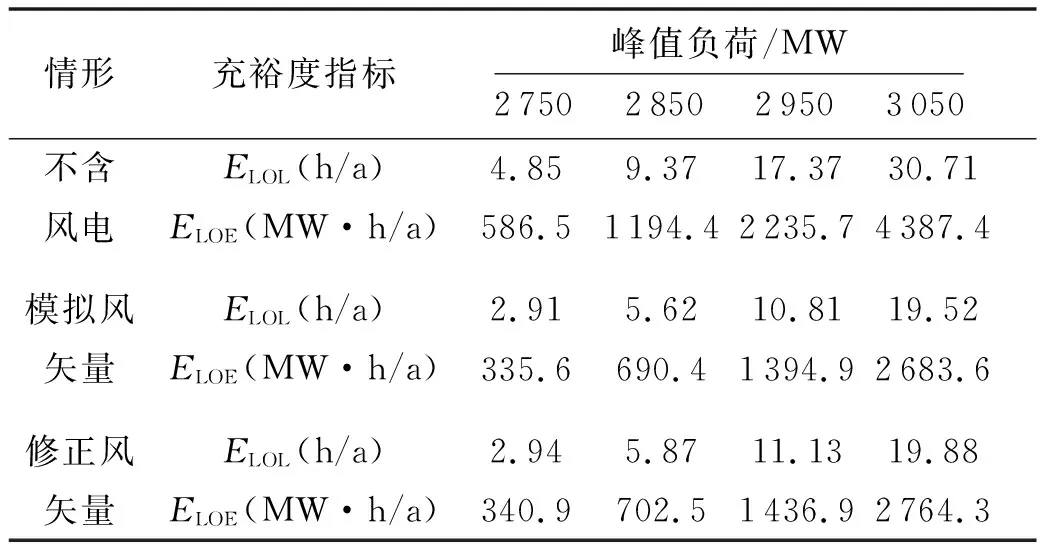
表8 不同峰值负荷下的系统充裕度指标

从表8可以看出：风电场的接入显著提高了电力系统的充裕度；系统峰值负荷是影响系统充裕度的重要因素，峰值负荷增大导致系统充裕度降低.在系统不同峰值负荷的条件下，兼顾日特性和季特性的修正风矢量模型与只计及日特性的模拟风矢量模型相比，其系统充裕度指标较低.结果表明在不同峰值负荷的条件下，忽略风矢量的季特性均可能使充裕度评估结果过于乐观.

5 结 论

本文提出了一种计及日特性和季特性的风矢量仿真模型，该模型基于正交分解法对风矢量进行聚类分析以划分马尔科夫状态空间，建立了计及日特性的风矢量马尔科夫链模型，并提出两组修正系数来描述风矢量的季节特征，对只计及日特性的仿真风矢量样本加以修正.本文的风矢量模型在考虑风速风向相关性的基础上，计及日周期特征与季节特征.

计及日特性的风矢量马尔科夫链模型，在统计特征上较为接近历史风矢量数据.提出一种同时修正仿真样本均值和标准差的季节系数，使风矢量仿真样本在保持统计特征的前提下呈现季节特征，从而提高了风矢量仿真模型的准确性.使用时序蒙特卡罗法对风矢量仿真模型加以应用，进一步证明了该模型的实用性和普适性.如果忽略风矢量的季节特征，使用未经修正的风矢量样本应用于含风电系统的时序蒙特卡罗法，会使充裕度评估结果过于乐观.本文验证了季特性对系统充裕度评估的结果，但仍存在不足之处，地形条件和风机高度也可能对风速分布产生影响，需要进一步验证以排除相关因素的干扰.