基于改进型斜率阈值法的滑坡降雨阈值分析

黄 耕 黄晓虎 易 武 周 迎

(1.湖北长江三峡滑坡国家野外科学观测研究站，湖北 宜昌 443002；2.三峡库区地质灾害教育部重点实验室(三峡大学)，湖北 宜昌 443002；3.防灾减灾湖北省重点实验室(三峡大学)，湖北 宜昌 443002)

滑坡在降雨作用下地下水位抬升会导致滑体的自重增加，并形成动水压力，滑体土体基质吸力丧失，以及滑带土体强度降低，滑坡逐渐变形，并最终失稳破坏[1-3].张友谊等[4]研究指出，降雨与滑坡灾害在时间与空间上有一定的一致性和滞后性，并存在一定的定量关系.Glade等[5]采用统计方法研究得出有无降雨诱发情况下滑坡发生的降雨量阈值.张珍等[6]通过统计分析降雨诱发滑坡的监测资料，总结出滑坡与降雨之间的规律.滑坡发生与降雨历时、降雨量、降雨强度有关[7].唐红梅等[8]采用Logistic回归方法，考虑当日最大小时降雨这一降雨因子进行综合分析，推导出重庆地区降雨型滑坡的预报模型.黄晓虎等[9]将滑坡进入蠕动变形阶段之后，预警关键判据定为前期降雨、当次降雨、位移速率，预警过程分为当次降雨和前期降雨+当次降雨两种模式.Chae等[10]通过降雨触发指数模型预警滑坡降雨强度，通过RTI模型预警滑坡变形响应时间.Kim等[11]将降雨历时和降雨强度阈值用于预测突发性滑坡的发生、边坡稳定性、降雨阈值、土水特征曲线等.陈志强等[12]在滑坡临滑阶段应用降雨量斜率阈值进行判断.上述对降雨量及其阈值研究取得大量成果，但对于降雨阈值研究，存在未考虑前期有效降雨量的问题.

本文以三峡库区钥匙湾滑坡为例，通过改进后的斜率阈值法找出滑坡类破坏点，类破坏点在不同观测时段n下，计算类破坏点累积有效降雨量[13-17]斜率阈值，并根据后期钥匙湾滑坡监测数据进行验证.

1 滑坡概况

1.1 滑坡基本特征

钥匙湾滑坡位于兴山县香溪河左岸，为珍珠潭滑坡的次级滑坡，其中珍珠潭滑坡左侧边界为自然冲沟，右侧边界为加油站东北侧山脊，前缘直抵香溪河，滑坡后缘可见出露岩土分界线，滑坡前后缘纵长410 m，均宽130 m，平均厚度约15 m，滑坡面积约3.9×104m2，总体积约59×104m3.2009年珍珠潭滑坡已经采用“挡土墙+格构护坡”治理.治理之后，于2019年12月6日现场巡查发现珍珠潭滑坡衍生出新的变形，钥匙湾滑坡位于珍珠潭滑坡内部右侧，坡体表层土体可见明显变形现象，剪出口位于民房外侧，坡体后缘高程约304 m，右侧边界为原珍珠潭滑坡右侧，左侧边界为山脊，滑坡前后缘纵长240 m，均宽80 m，滑坡面积2.86×104m2，平均厚度约7.5 m，体积21.45×104m3，工程地质平面如图1所示，工程地质剖面如图2所示.

图1 钥匙湾滑坡工程地质平面图

图2 钥匙湾滑坡1-1工程地质剖面图

钥匙湾滑坡滑体按岩土体性质可分为：上部为碎块石土，灰-黄褐色，可塑，土石比为3∶7～4∶6；中部为紫红色泥质粉砂岩、粉质黏土夹碎块石，中密～密实；下部含有少量次圆状半风化粉砂岩质碎块，粒径5～10 cm，粉质黏土为硬塑～可塑状，土石比为6∶4～5∶5.

滑带平均厚度15 cm，平均倾角35°，主要为粉质黏土夹碎石，中密，紫褐色，可塑状.碎石成分为紫红色粉砂岩，力学性质差，抗风化能力较弱，在干湿交替作用下，极易风化成土状.滑床基岩岩性为侏罗系下统香溪组(J1x)长石石英砂岩、紫红色泥质粉砂岩，产状250°∠41°.

1.2 滑坡历史变形特征

前期变形以原珍珠潭滑坡为主体，最早可追溯到1999年，滑坡中部出现地面下陷，下错0.3～0.5 m.至2005年，滑坡中上部滑体发生局部滑塌，滑坡壁出现，靠近左侧边界古墓变形破坏，坡体中部道路错台.

鉴于此，于2009年采取“挡土墙+格构+浆砌石护坡”的治理措施，滑坡变形休止.2017年10月，挡土墙后侧区域发现地表裂缝T1～T6，裂缝持续发育，且呈现与滑塌方向相向特征.2018年9月，格构和浆砌石护坡上发现裂缝T7～T9，变形扩大到南侧治理工程，同时，格构梁开始出现变形.10月，挡土墙后侧裂缝继续扩展，斜坡稳定性逐渐降低.11月，上方土体滑动，堆积在挡土墙顶部，滑塌后缘壁形成(如图3所示).

图3 滑坡变形特征

2018年12月，房屋周围出现一条近南北向拉张裂缝T10，长约3 m，宽约2～8 cm，墙体、房屋与地基连接处出现多处裂缝T11～T12.2019年，受持续降雨作用，裂缝T7～T9继续扩展，挡土墙出现同向裂缝，挡土墙阻滑力逐渐降低，至2020年6月27日，当地遭受40 mm的大雨，挡土墙变形加剧，墙体两条主裂缝LF1长度约3 m，宽度约10～20 cm，LF2长约3.5 m，宽度约10～15 cm，挡土墙南段剪切断裂，向外剪出约5～15 cm，挡土墙后侧的格构护坡局部拉裂破坏，治理工程裂缝全部贯通，调查发现钥匙湾滑坡大小裂缝共计13条.

钥匙湾滑坡采用GNSS监测网络对滑坡位移进行实时监测，包括基准点YS0、监测点YS1、YS2、YS3.滑坡累积位移与降雨量关系如图4所示.

图4 钥匙湾滑坡累积位移-降雨量关系曲线

综合分析认为：钥匙湾滑坡在降雨作用下，连续降雨时间长且降雨强度大时，滑坡变形速率急剧增大，后趋于平缓；当降雨时间不连续且降雨强度小或无降雨时，滑坡几乎无变形.因此，钥匙湾滑坡的变形受降雨影响较大，属于三峡库区典型的降雨型滑坡.

2 改进型斜率阈值法

钥匙湾滑坡属于三峡库区内典型的降雨型滑坡，降雨诱发滑坡大致可分为两个阶段[14]：

1)滑坡发生前一定时间内的降雨过程，此阶段降雨入渗，会使滑坡土体饱和，滑坡重量增加，同时孔隙水压力随之增加，抗剪切强度降低，使滑坡趋于滑动的临界状态.

2)当次固定时间内的降雨直接导致滑坡发生并最终失稳破坏.

因此，研究滑坡两个阶段的降雨量是研究滑坡降雨斜率阈值的关键.

斜率阈值法[12]是指根据累积变形曲线分析滑坡变形特性，引入“类破坏点”、“降雨量斜率”、“斜率阈值”等针对滑坡的定量预报.但研究方法中滑坡变形前期降雨是累积降雨量，未考虑降雨过程中的雨水流失、蒸发等原因，所求降雨量斜率阈值偏大.因此，应考虑前期降雨对滑坡有影响的那部分降雨量，本文引入有效降雨量、降雨衰减系数，对斜率阈值求取进行改进，所得出结果更精确.对钥匙湾滑坡前140期监测数据分别求取滑坡累积位移的类破坏点、累积有效降雨量、平均累积有效降雨量斜率阈值，并对后40期监测数据进行验证分析.该方法总结为以下3个步骤[18]：

1)分析滑坡的累积位移与降雨量、时间三者之间关系，应用降雨斜率单变点确定滑坡的类破坏点；

2)由滑坡每个类破坏点的前期累积有效降雨量与观测时段的关系，分析得出累积有效降雨量斜率，最后加权平均得出累积有效降雨量斜率阈值；

3)在选定的观测时段下，做出监测时间与滑坡降雨量斜率曲线，添加一条累积有效降雨量斜率阈值直线，处于直线下方的观测点，降雨量斜率小于累积有效降雨量斜率阈值，则滑坡处于稳定状态，反之，则滑坡很有可能急剧变形，导致失稳破坏.

2.1 求类破坏点

数学问题中曲线的拐点是指改变曲线向上或向下方向的点，直观地说，拐点是使切线穿越曲线的点(即曲线的凹凸分界点).当降雨达到一定强度时，降雨型滑坡变形急剧增大，累计位移曲线在此期间有一个明显的拐点，将其称为类破坏点[18].

斜率单变点求取类破坏点步骤如下:

1)寻找探索点序列ti.对监测时间划分等距时间区段，取等距时间区段的中点为一个探索点，以此类推所有时间区段的探索点构成一组序列ti.

(1)

(2)

对ΔY(ti)序列，再计算其二阶差分ΔY2(ti)，即:

ΔY2(ti)=ΔY(ti)-ΔY(ti-1)

(3)

4)随着序列ti从小到大计算，寻找序列中出现的最大值ΔY2(ti)，其所在的区间为[ti-1，ti]，即斜率单变点所在的区间.再计算前后相邻的两个区间的ΔY2(ti-1)、ΔY2(ti+1)，将两个区间的ΔY2(ti-1)、ΔY2(ti+1)线性内插，求得类破坏点t*.计算公式如下：

t*=ti-1+

(ti-ti-1)

(4)

2.2 有效降雨量斜率阈值

有效降雨量是指诱发滑坡发生的那部分降雨.滑坡前期的一个降雨过程中有多次降雨，距离当次降雨时间越长的降雨其有效降雨对滑坡影响越小，只有部分降雨量对滑坡有作用，1980年Crozier在引入滑坡地质灾害降雨阈值的研究中[14]有效降雨量用下式来表示：

Da=D0+λD1+λ2D2++λ3D3+…+λnDn

(5)

式中：Da为有效降雨量；D0为当天降雨量；D1为次日降雨量，依此类推，n为滑坡发生前的天数；λ为降雨衰减系数.

降雨衰减系数可采用如下公式计算[19]:

(6)

通过公式(4)求取滑坡的类破坏点t*后，再将类破坏点t*前某一观测时段n的有效降雨量累加得到累积有效降雨量ΔD，作出各个类破坏点的累积有效降雨ΔD与观测时段n的关系图，求出每个点的线性回归系数Dk(k=1，2，3，…，x；x为斜率单变点的个数)，将Dk称为第k个类破坏点的有效降雨量斜率.一个类破坏点的值或几个Dk类破坏点的Dk值的加权平均值为累积有效降雨量斜率阈值[17]，简称斜率阈值D，即:

(7)

3 实例验证

3.1 求取类破坏点

钥匙湾滑坡监测数据源于湖北省三峡库区钥匙湾滑坡应急监测点，累计位移曲线如图4所示.受降雨作用滑坡变形集中于5～10月，本文研究数据为监测点YS2的累积位移和当地降雨量，选取共180期监测数据(2020年5月2日～2020年10月29日)进行分析.

3.2 有效降雨量斜率阈值

计算得出滑坡类破坏点后，选取观测时段n=1，3，6，…，15，并计算观测时段内的前期累积有效降雨量ΔD(如图5所示).

图5 类破坏点不同n值下累积有效降雨量

分析如下：当观测时段n>6时，3个类破坏点的前期累积有效降雨量增长速率平缓；但观测时段n≤6时，3个类破坏点累积有效降雨量增长速率急剧增大.

选取观测时间段n=1，2，…，7并计算观测时段内的前期累积有效降雨量ΔD(如图6所示).在各类破坏点前n天，累积有效降雨量同观测天数呈线性相关.

图6 类破坏点前7 d累积有效降雨量

由图5、图6知不同的观测时段影响到累积有效降雨量ΔD变化，在观测时段n≤6时，累积有效降雨量与观测时段呈正相关，可通过公式(8)分析平均累积有效降雨量斜率:

(8)

式中：Dk为平均累积有效降雨量斜率；ΔD为平均累积有效降雨量；n为观测时段.

同时，时间间隔d的选取影响累积有效降雨量、平均累积有效降雨量斜率，见表1、表2.

表1 累积有效降雨量随观测时段、时间间隔变化表

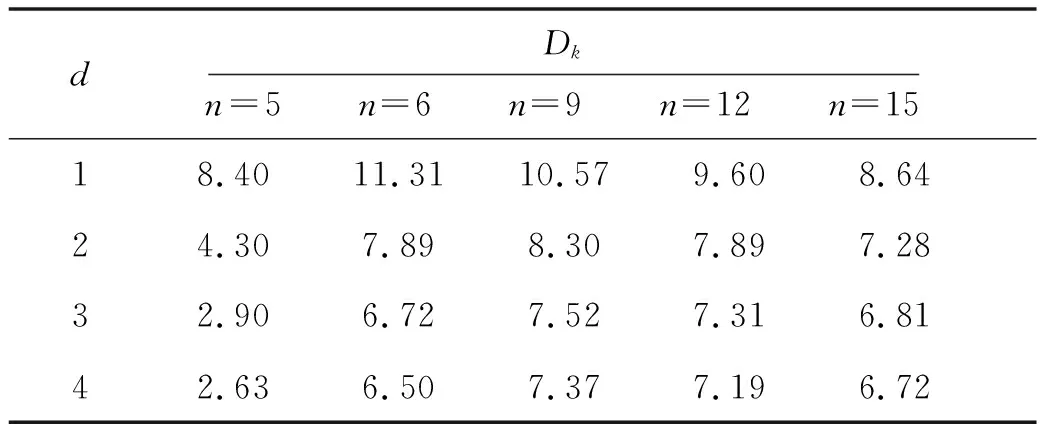
表2 平均累积有效降雨量斜率随观测时段、时间间隔变化表

由表2可知，在相同观测时段下，Dk随着时间间隔的增大而减少；在相同时间间隔下，随着观测区段的增大，Dk随着观测时段先增大后减小.观测时段内累积位移进入类破坏点所需的累积有效降雨量越大，降雨量斜率越大，平均累积有效降雨量斜率越大.因此，找出滑坡3个类破坏点的平均累积有效降雨量斜率，加权平均得出的降雨量斜率越大.不同观测时段下降雨量斜率随监测时间变化如图7所示.

图7 不同观测时段有效降雨量斜率(d=1)

3.3 后期监测数据验证分析

由上述分析得知观测时段与时间间隔是影响Dk的主要因素.

1)当观测时段n≤6时，此时降雨量比较集中，有效降雨量各个类破坏点观测时段n点数太少，随机性太强，未能反映观测时段n对整体有效降雨量的影响；

2)n>6时计算得到的累积有效降雨量斜率增速趋于平缓，未能体现有效降雨量与观测时段n相关关系.

因此，观测时段n选取累积有效降雨量斜率单变点，时间间隔d最小时，滑坡的平均累计有效降雨量斜率最大，计算3个类破坏点的前期累积有效降雨量，求出累积有效降雨量斜率，通过加权平均得累积有效降雨量斜率阈值，即钥匙湾滑坡的降雨斜率阈值D=10.83.取降雨斜率阈值D与累积有效降雨量斜率、时间三者的关系曲线(如图8所示).

图8 有效降雨量斜率阈值预报图

前文抽取前140 d降雨监测数据进行原理分析，对剩下的40 d的样本监测数据进行预测预报.如图8所示，在监测数据前140 d中，t1=57(与实际相差2 d)，t2=63(与实际相差0 d)，t3=81(与实际相差2 d)，验证效果较好.在监测数据剩余40 d的数中，当监测天数为153 d时，有效降雨量斜率为10.9，大于降雨斜率阈值D.表明当天降雨量斜率达到滑坡预测的降雨斜率阈值，即滑坡处于变形状态，累积位移发生变化，结合监测数据得知与实际相差1 d，当天累积位移较前6 d增加了5.3 mm，预测效果良好.

4 结 论

本文以钥匙湾滑坡为例，利用改进型斜率阈值法求取有效降雨量斜率阈值，经过验证分析预测结果较为理想，主要得到以下结论：

1)不同类破坏点在观测时段n≤6时，累计有效降雨量与观测时段n呈正相关关系.

2)随观测时段n增大，平均累积有效降雨量斜率先增大后减小.

3)根据改进型斜率阈值法计算求出钥匙湾滑坡有效降雨量斜率阈值D为10.83，表明当钥匙湾滑坡的降雨量斜率超过10.83，滑坡可能进一步变形破坏.

4)监测数据后40 d数中，当监测天数t=153时，有效降雨量斜率为10.9，大于降雨斜率阈值D，累积位移发生变化，结合监测数据得知与实际相差1 d，当天累积位移较前6 d增加了5.3 mm，预测效果良好.