混凝土静态破碎剂膨胀性能及其破碎孔径优化
钟 振 杨熙华 顾杨圣 娄 荣 夏才初 包春燕
(1.绍兴文理学院 土木工程学院,浙江 绍兴 312000;2.绍兴文理学院 岩石力学与地质灾害实验中心,浙江 绍兴 312000;3.绍兴市交通投资集团有限公司,浙江 绍兴 312000;4.华汇工程设计集团股份有限公司,浙江 绍兴 312000;5.同济大学 地下建筑与工程系,上海 200092)
静态破碎技术是利用破碎剂遇水膨胀和硬化的特性,将破碎剂与水按一定比例拌和形成浆液,灌入含注浆孔的构件,通过浆液膨胀产生的膨胀压使构件开裂破碎的一种技术.该技术是对爆破技术的重要补充和发展,且相较于爆破拆除,静态破碎是一个无声、缓慢的渐进过程,可有效减少破碎过程中的振动、粉尘及噪声等污染,加上静态破碎剂运输、保管方便,目前静态破碎技术已被广泛应用于岩石破碎、工程拆除和矿山开采中[1].
静态破碎效果与破碎剂的膨胀性能密切相关,其中膨胀压是表征破碎剂膨胀性能最重要的指标,其大小与水剂比、破碎孔的孔径等因素相关.水剂比越小,所产生的膨胀压力越大,但水剂比减小会影响浆液的流动性,为兼顾膨胀压力和施工的可灌性,水剂比一般介于1/4~1/3之间.此外,为防止喷孔现象,破碎孔的尺寸通常不大于50 cm.温尊礼等[2]提出了一种可用于大孔径的静态破碎技术,通过自制的扩孔钻头,并制备机械堵孔器解决了大孔径静态破碎的喷孔问题,其最大炮孔尺寸达到100 mm,大大拓宽了静态破碎技术的使用范围.姜楠等[3]则进一步使用数据拟合方法,修正得到了大孔径静态破碎时岩石内应力分布的计算方程,通过该方程推导得到的布孔参数准确,可用于实际工程中.
针对混凝土或岩石的静态破碎过程(裂隙萌生、扩展和贯通)及破碎机理,国内外学者采用理论分析、数值模拟和试验研究等方法开展了大量的分析和测试,取得了丰硕的成果.唐烈先等[4]采用物模试验和数值试验相结合的方法研究了单孔方形混凝土的静态破碎过程,观察到了裂缝纹从萌生、扩展到最终贯通的全过程.杨仁数等[5]用高速相机捕捉了静态破碎剂作用下含两翼切槽孔试件裂纹的萌生、扩展到最后的失稳过程,通过分析发现裂纹扩展速度和加速度的变化呈先增后降的趋势.姜智盛等[6]通过混凝土块的静态破碎试验研究了孔径与约束比对破碎效果的影响,发现当约束比小时,开裂时间主要受孔径影响;约束比大,则约束比对开裂时间影响比孔径更大.娄荣等[7]等则最早将扩展有限元方法应用于模拟钢筋混凝土梁的静态破碎过程,研究发现梁的裂缝扩展以Ⅰ型裂缝为主,破碎过程可分为弹性变形、裂缝稳定扩展和裂缝失稳扩展3个阶段,并通过应变能释放率计算得到了临界破碎压.
为优化静态破碎孔孔径,充分发挥破碎剂的膨胀性能,降低破碎成本.本研究从静态破碎剂的膨胀性能出发,通过外管法测定静态破碎剂在不同孔径下的最大膨胀压.在此基础上,应用ABAQUS软件建立含预设静态破碎孔的混凝土模型,并通过扩展有限元方法(extended finite element method,XFEM)模拟分析含不同孔径破碎孔混凝土的裂隙萌生、扩展及贯通过程.同时,引入能量释放率法则,从能量角度分析裂纹扩展过程及规律,计算破碎定尺寸混凝土试块所需的最小孔径,为工程实践提供参考.
1 静态破碎剂膨胀性能试验
为了掌握破碎剂的膨胀性能,选用广西贺州生产的飞鹰牌静态破碎剂,并对破碎剂的膨胀性能进行测试:包括膨胀率试验和膨胀压试验.首先通过开展不同水剂比、拌和温度下的体积膨胀率试验,获得最大膨胀率对应的水剂比和拌和温度;随后在相应的水剂比和温度条件下,通过外管法测定不同孔径条件下静态破碎剂可产生的最大膨胀压.
1.1 膨胀率试验
膨胀率试验的装置为一个立方铁盒,尺寸200 mm×200 mm×200 mm,如图1所示.综合考虑施工的可灌性和膨胀压力,试验中水剂比介于0.28~0.35,拌和水温度介于25℃~45℃,具体试验条件见表1.在试验过程中,取适量的静态破碎剂,按设定的水剂比与水拌和,制成浆液倒入方形铁盒,迅速整平后用钢直尺量取破碎剂在4个边角点的初始高度,取其平均值为h0.膨胀过程中的温度变化用数字测温仪测量,待膨胀结束温度下降后,再次量取4个边角点的高度,取其平均值为h,通过计算可获得静态破碎剂的膨胀率α=(h-h0)/h0.

图1 静态破碎剂膨胀率测试
不同水剂比、拌和水温下的膨胀率计算结果见表1.从表1可知,膨胀率明显受到水剂比的影响,且膨胀率随着水剂比的降低而升高,当水剂比为0.35时,膨胀率为3.16,而当水剂比降低至0.28时,膨胀率增加至3.48,体积膨胀增幅超过10%,但膨胀率受拌和水温的影响则较小.不同水剂比、温度条件下反应温度随时间的变化曲线如图2所示.
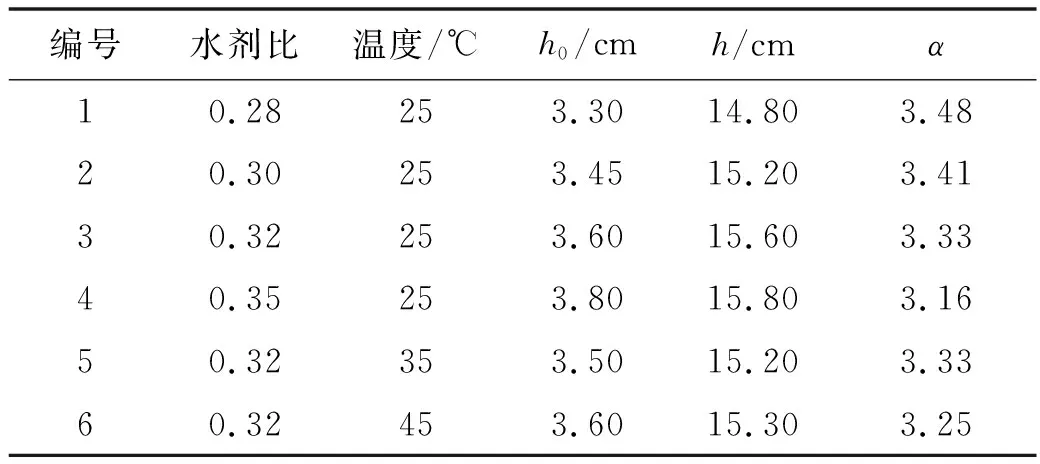
表1 静态破碎剂膨胀率试验条件及结果
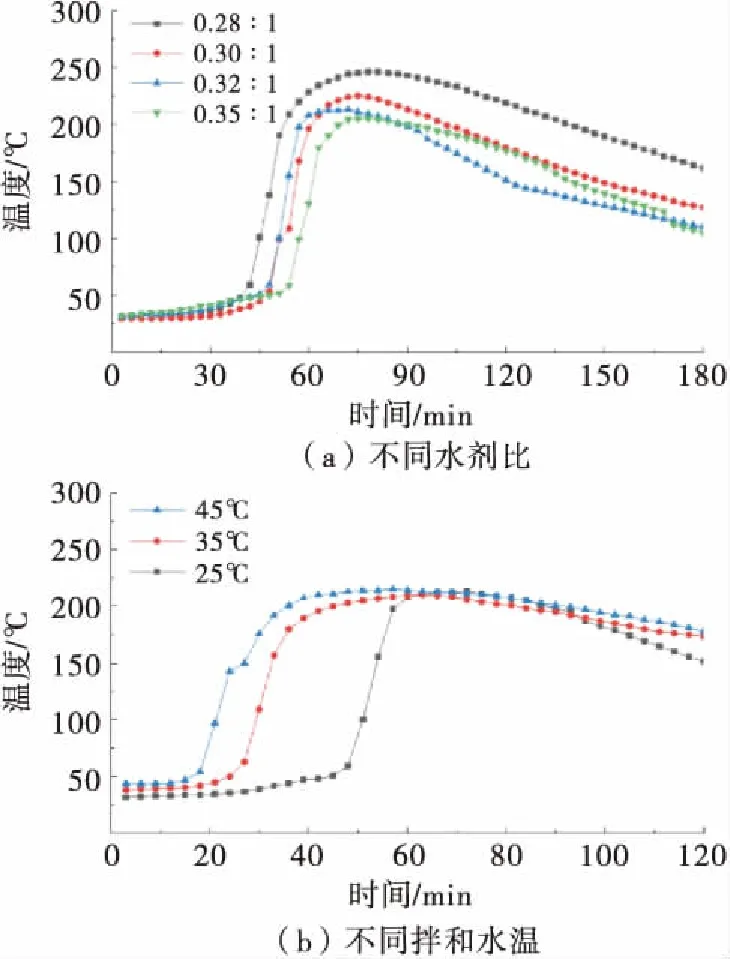
图2 静态破碎剂温度-时程曲线
从图2可知,静态破碎反应呈现出缓-急-缓的趋势,初始反应时间约介于20~50 min之间,且随水灰比的降低、拌和水温的升高而缩短;随着反应进程,释放出大量的热,温度迅速上升,短时间内超过100℃,随后,温度达到顶峰并逐渐下降.综上,为获取最优膨胀压,本文选择在水剂比0.28和拌和水温25℃的条件下开展静态破碎剂膨胀压测试试验.
1.2 膨胀压试验
膨胀压采用《JC 506—2008无声破碎剂》建议的外钢管间接测定法测定[8].图3、图4为试验用钢管及应变片布置,试验选用5种内径为24、28、32、36、39 mm的薄壁钢管,管长和壁厚恒定,分别为1 000 mm和3 mm,在管长三等分点沿环向分别贴应变片(BX120—20AA,浙江黄岩测试仪器厂),应变数据采用动态应变仪(TST3828E,江苏泰斯特电子设备制造有限公司)采集,再通过公式(1)换算得到静态破碎剂的径向膨胀压:

图3 不同直径钢管 图4 应变片粘贴位置示意图
p=Es(K2-1)[εθ/(2-v)]
(1)
式中:p为静态破碎剂的膨胀压;Es为钢管弹性模量,取2.06×1011Pa;K为钢管外径与内径的比值;εθ为钢管的环向应变;v为钢管的泊松比,取0.3.
由于不同位置的3个应变片所测的应变随时间变化趋势比较一致,为方便表示,以下只展示位于中间2号应变片的测量和计算结果,但在求解最大膨胀压时,仍取3个应变片值求平均.测得(计算)的2号应变片应变、膨胀压随时间演变曲线分别如图5和图6所示.

图5 应变-时间曲线(2号应变片)

图6 膨胀压力-时间曲线(2号应变片)
从应变曲线图5可知,随着管径的增加,破碎剂开始膨胀时间有所提前.由图6可知,随着钢管内径的增加,管内所能容纳的破碎剂浆液相应地增多,所产生的膨胀压亦增加,内径24 mm钢管产生的最大膨胀压仅为12.2 MPa,内径39 mm钢管产生的最大膨胀压则达25.34 MPa.
1号、2号和3号应变片求得的峰值膨胀压见表2,不同孔径下的最大膨胀压取3个应变片膨胀压的平均值.在钢管直径为24~39 mm范围内,最大膨胀压Pa随孔径的增大呈线性增加趋势,这与河野俊夫的试验研究成果一致[9].
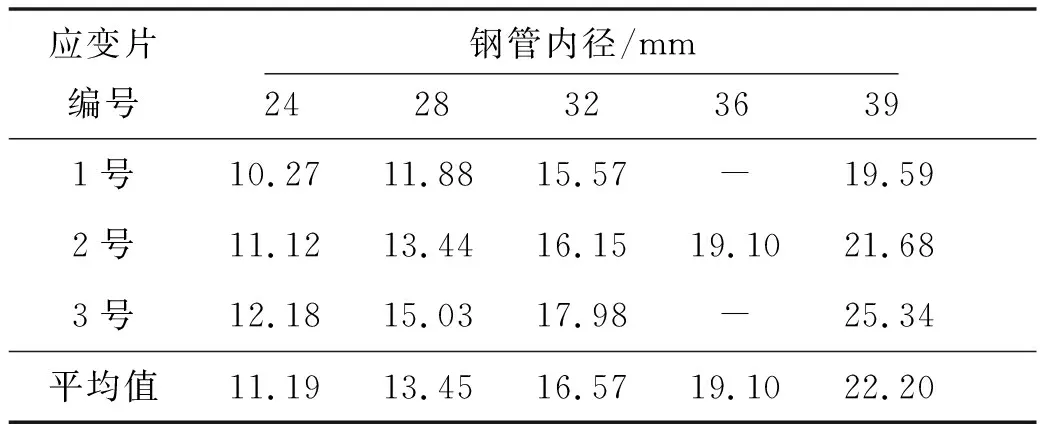
表2 不同孔径下最大膨胀压 (单位:MPa)
2 混凝土静态破碎数值模拟研究
2.1 扩展有限元法基本理论
扩展有限元法的核心思想是用可以描述间断特性的富集函数来表征计算区域内的不连续,在计算过程中,不连续场的描述与有限元网格无关,在处理断裂问题方面有较好的优越性.扩展有限元法的位移函数在常规有限元的基础之上增加了反映单元内部裂缝面的加强函数[10-11]:
(2)
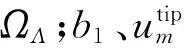
(3)
(4)
式中:X为高斯点;X*为高斯点X在裂缝面上的垂直投影;n为裂缝上X*处的单位外法向矢量,为反映裂缝面位移的不连续,规定H(x)在裂纹上方时取1,在裂纹下方时取-1;r和θ为裂尖处极坐标.
2.2 基于能量释放率的扩展分析
能量释放率是从能量耗散角度提出的判断裂纹扩展的宏观指标,混凝土损伤的本质是能量的耗散和释放的过程.模型的损伤可分为无裂缝阶段与裂缝扩展阶段两个过程,利用最大主应力研究无裂缝阶段,判断材料的起裂位置,其表达式为:
(5)

(6)
式中:Gequivc为临界断裂能释放率,当裂缝尖端能量释放率大于该值时,则裂缝尖端开裂,裂缝扩展;n′为各向应力在其对应位移上做的功;GⅠC、GⅡC分别为Ⅰ型裂缝(张开型)和Ⅱ型裂缝(滑移型)断裂韧度;GⅠ、GⅡ、GⅢ分别为Ⅰ型裂缝,Ⅱ型裂缝和Ⅲ型裂缝(撕裂型)的能量释放率,采用虚拟裂缝闭合技术计算,方程如下[13]:
(7)
(8)
(9)

2.3 三维混凝土模型
如图7所示,使用ABAQUS数值软件建立边长为150 mm的立方混凝土试块模型,模型中间预设不同直径(24、26、28、30 mm)的破碎孔,以研究不同孔径下的破碎效果,静态破碎剂可产生的最大膨胀压根据孔径大小通过图6中膨胀压-孔径关系曲线线性内插得到.模型抗压和抗拉强度分别取20.1和2.01 MPa;泊松比取0.2,弹性模量取29.5 GPa,混凝土的临界应变能释放率取120 N/m[14].计算网格采用C3D8R单元(图7(a)),位移上约束模型正面和背面的法相位移(图7(b)),在破碎孔内施加膨胀压(图7(c)),并根据孔径的大小逐级增加至相应的最大膨胀压力.

图7 三维混凝土试块模型
2.4 模拟结果及分析
基于扩展有限元法对混凝土静态破碎过程进行模拟,裂纹扩展判别使用能量释放率判断准则.图8为含不同破碎孔孔径的混凝土在相应最大膨胀压作用下的最终破碎状态.

图8 破碎状态及裂缝分布图
从图8可知,除孔径24 mm的模型在达到最大膨胀压力时裂缝未贯穿混凝土,其余孔径下裂缝均已贯通.静态破碎产生的贯通主裂缝数量介于2~4条,且主裂缝主要沿着最小抵抗线方向扩展和贯通,这与桂良玉[13]的理论分析一致.同时,主裂缝的数量随孔径的增加有减小的趋势,孔径24 mm的模型产生了4条主裂缝(图8(a)),而孔径30 mm的模型只产生两条主裂缝(图8(d)),这可能是先贯穿的裂缝释放了孔内的膨胀压,使其膨胀力不能完全发挥,从此角度亦可说明,破碎孔孔径并非越大越好.通过进一步分析发现,贯穿相同尺寸混凝土试块所需的膨胀压力随孔径的增加略有降低(见表3),孔径为26 mm的模型在膨胀压力达到11.28 MPa时裂缝贯通,而当孔径为30 mm时,膨胀压力达到10.7 MPa裂缝便贯通;但混凝土模型的起裂压力几乎不受孔径大小的影响,其主要受混凝土本身的抗拉强度控制.
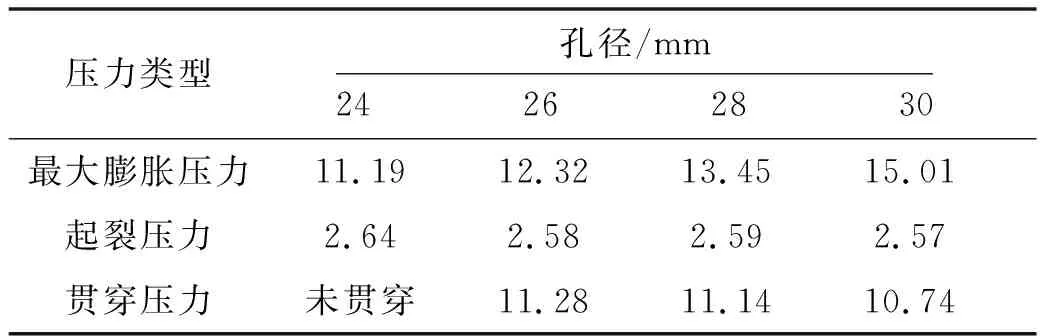
表3 模型的起裂、贯穿压力 (单位:MPa)
如果以裂缝贯通作为试样破碎的标准,那么破碎边长为150 mm的立方体混凝土试块所需的最小的破碎孔孔径为26 mm,此即为最优孔径.图9为含26 mm破碎孔的混凝土试块在静态破碎作用下的应力变化以及裂纹萌生、扩展和贯通过程,从主裂缝数量和开裂方向来看,数值模拟和试验结果较为吻合.如图9(b)所示,当膨胀压力p达到2.58 MPa,裂缝开始萌生;随着膨胀压力的增加,裂缝进一步扩展,扩展方向沿着最小抵抗线方向,直到p=11.28 MPa时,裂缝贯通(图9(c)).

注:(a)~(d)为数值模拟结果;(e)~(h)为试验结果.
图10为能量释放率随膨胀压力的变化曲线,根据曲线可将裂纹扩展分为3个阶段:第1阶段为未裂阶段(p<2.58 MPa),此阶段膨胀压力小于混凝土的抗拉强度,无裂纹产生;第2阶段为裂缝萌生、扩展阶段(2.58 MPa≤p<11.28 MPa),当p=2.58 MPa,能量释放率发生突变,表明裂缝起裂,且随着膨胀压力的增加,能量释放率逐渐增大,裂缝不断扩展;第3阶段为裂缝贯通阶段(p≥11.28 MPa),p=11.28 MPa时,能量释放率突增,说明裂纹贯通,随着膨胀压的继续增大,混凝土试样逐渐破碎.
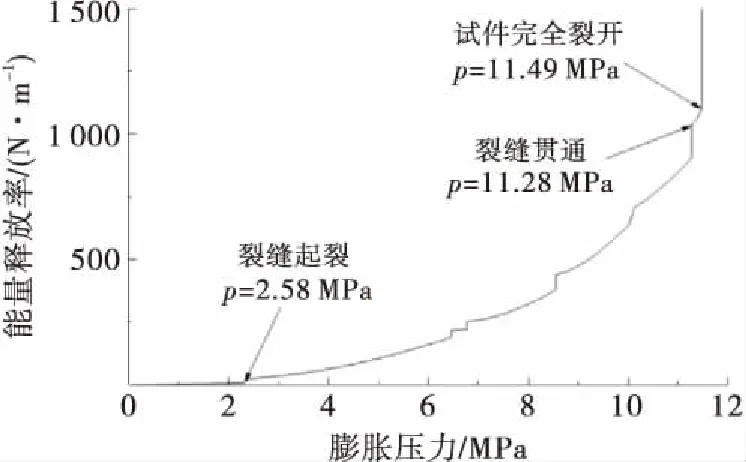
图10 能量释放率-膨胀压力曲线(26 mm)
3 结 论
本文从静态破碎剂的膨胀性能出发,通过膨胀压力测试试验获得不同破碎孔径下静态破碎剂可以产生的最大膨胀压;在此基础上,基于扩展有限元方法模拟混凝土试块静态破碎过程,采用能量释放率作为裂纹扩展的判据,探索混凝土试块静态破碎的最优孔径.具体研究成果如下:
1)最大膨胀压力随钢管内径的增加而增大,两者近似呈线性关系.
2)基于扩展有限元模拟了含不同孔径混凝土试块在静态破碎中裂纹萌生、扩展和破碎的全过程.模拟结果显示:静态破碎产生2~4条主裂纹,且主裂纹沿着最小抵抗线的方向扩展并贯穿;当破碎孔径≥26 mm,静态破碎剂产生的膨胀压足以破碎边长为150 mm的立方试块,此为最优孔径.
3)采用能量释放率理论进一步分析最优孔径下混凝土裂纹的扩展过程,发现裂纹扩展分为3个阶段:第1阶段为无裂纹阶段(p<2.58 MPa);第2阶段为裂纹萌生、扩展阶段(2.58 MPa≤p<11.28 MPa),当p=2.58 MPa能量释放率发生突变,表明裂纹萌生,且随着膨胀压力的增加,能量释放率逐渐增大,裂缝不断扩展;第3阶段为裂纹贯通阶段(p≥11.28 MPa),当p=11.28 MPa时,能量释放率突增,裂纹贯通,随着膨胀压的继续增大,混凝土试样逐渐破碎.

