深厚覆盖层塑性混凝土心墙坝应力变形特性研究

陆嘉伟 张继勋，2 任旭华，3

(1.河海大学 水利水电学院，南京 210098；2.河海大学 水利学科专业实验教学中心，南京 210098；3.水安全与水科学协同创新中心，南京 210098)

在大坝施工及运行过程中，由于混凝土心墙与相邻过渡料力学性能的巨大差异，导致心墙与坝体变形不协调，会使心墙承受很高的拉应力和压应力，从而导致墙体出现裂缝，降低坝体防渗效果，威胁大坝的安全稳定运行[1-3].基于此，有关专家通过掺加膨润土、黏土等材料来代替混凝土中大部分的水泥，发明了塑性混凝土[4-5]，此种混凝土是一种柔性材料，具有低强度、低弹性模量和大应变等特点，可以很好地与软性基础相适应，同时又具有很好的防渗性能，塑性混凝土的出现引起了国内外工程界的高度关注.

对于塑性混凝土防渗墙的应力变形特性，许多学者展开了数值模拟研究.沈珠江等[6]对三峡二期高土石围堰的塑性混凝土低双墙方案进行了数值计算，分析了在设计条件下墙体的应力变形是否在安全范围内；李烽等[7]以某深水高土石围堰为例，研究分析考虑湿化作用的不同运行水位下塑性混凝土防渗墙的应力变形特性；李宗坤等[8]以某防渗加固的均质土坝为例，研究了加固后墙体的应力变形特性，并分析了弹性模量系数K对其应力变形的影响.

很多学者对塑性混凝土心墙的应力变形作了大量的数值计算，但目前大多以二维计算为主.本文以云南省某塑性混凝土心墙砂砾石坝为例，对其进行三维非线性有限元计算，分析心墙及坝体在竣工期及蓄水期的应力变形特性，并研究了不同覆盖层厚度对其应力变形的影响，以期对该坝的设计施工提供参考.

1 工程概况

云南省某塑性混凝土心墙砂砾石坝，工程等别为Ⅳ等，坝顶高程3 408.20 m，最大坝高31 m，坝顶长363 m，坝顶宽6 m，大坝上游为二级，坡比均为1∶2.4，下游坝坡二级，坡比从上至下分别为1∶2.2和1∶1.5，在高程3 384.79 m处设计2 m宽马道，此高程以下为排水棱体，在大坝下游砂砾石填筑区与基础接触处铺设2 m厚堆石水平排水层，连接混凝土心墙下游过渡料与排水棱体.塑性混凝土心墙中心线位于坝轴线处，采用等厚度(80 cm)设计，坝体典型横剖面图和纵剖面图如图1～2所示.

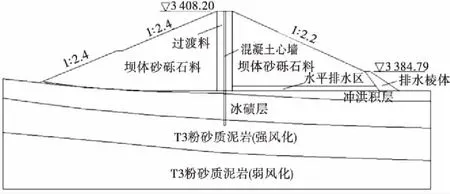
图1 大坝典型横剖面图

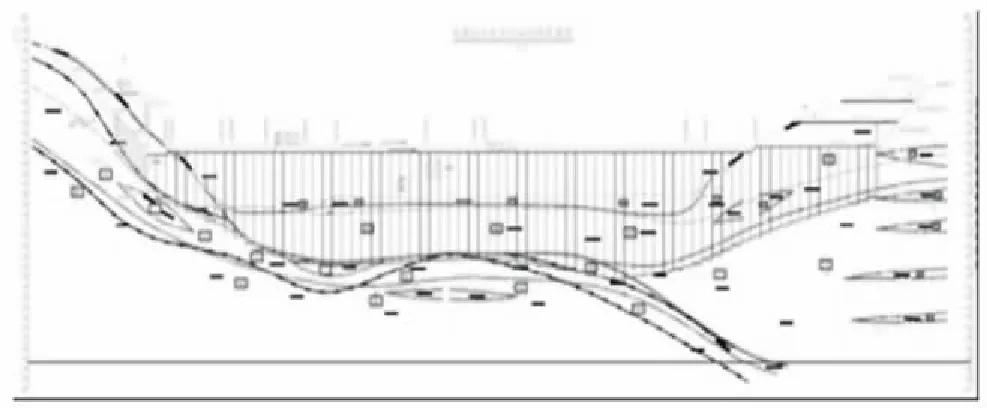
图2 大坝典型纵剖面图

该坝左岸覆盖层厚度达到30 m左右，而右岸覆盖层厚度只有10 m左右，坝基不均匀变形可能性大.尽管坝不高，坝坡较缓，但塑性混凝土心墙在施工及运行过程中易产生裂缝，因此需要计算分析心墙的薄弱部位，从而采取相应措施确保安全.

2 计算原理与方法

本文采用大型有限元软件ABAQUS进行数值计算，主要涉及两方面的非线性计算：一是本构模型采用了非线性邓肯-张E-B模型；二是心墙与过渡料之间的接触模拟.

2.1 坝体材料本构模型

邓肯-张E-B模型能够较好地反映塑性混凝土材料的非线性，计算结果可以真实地反映坝体的应力变形规律，是被工程界所接受的最为经典的本构模型.因此，本文采用邓肯-张E-B模型[9]来模拟填筑料的本构关系，计算公式如下：

弹性模量Et：

(1)

体积模量Bt：

(2)

式中：K为弹性模量系数；n为弹性模量指数；pa为大气压力；Rf为破坏比；c、φ为强度指标；Kb为切线体积模量系数；m为切线体积模量指数.

2.2 接触本构模型

ABAQUS中模拟接触问题时需要定义接触面的法向模型和摩擦模型[10].因此本文接触面的法向行为采取硬接触，摩擦模型采用罚刚度算法.其在ABAQUS中运用Coulomb定律计算这种摩擦力，公式如下：

τcrit=μp

(3)

式中：τcrit为接触摩擦力；μ为摩擦系数；p为两接触面间的法向应力.

3 工程实例有限元模型

3.1 计算模型与边界条件

根据塑性混凝土心墙砂砾石坝的横纵剖面图，建立三维有限元计算模型.为消除边界影响，上、下游和向左、右岸各自延伸30 m，基础向深部延伸80 m，将各地层全部包括.计算中模型坐标采用笛卡尔坐标系，x方向为坝轴线方向，y方向为水流方向，z方向竖直向上.模型主要采用八节点六面体等参单元，并在塑性混凝土心墙与过渡层之间设置接触面，模型单元数共92 111个，节点98 340个，计算网格模型如图3所示.

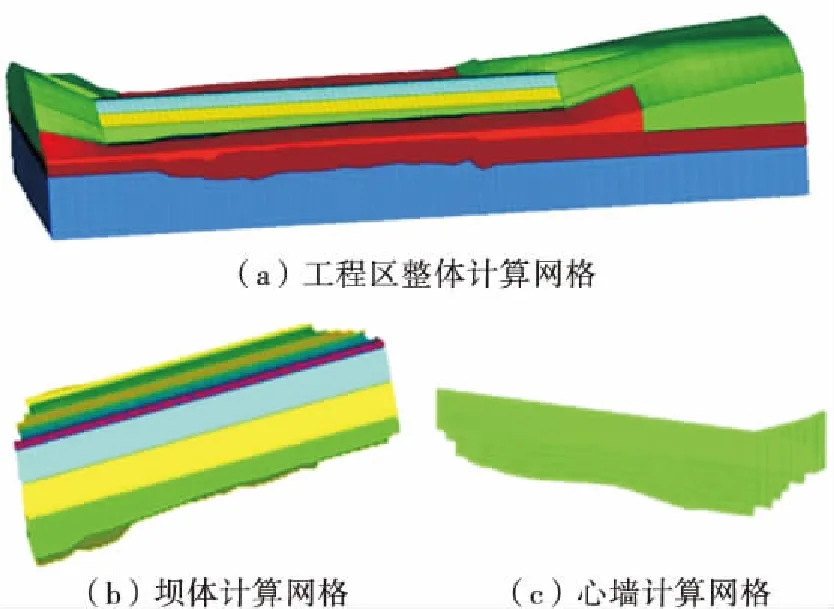
图3 有限元计算网格

计算过程中，边界条件设为：模型底部固定z方向位移，左右侧固定y方向位移，前后侧固定x方向位移.

3.2 计算参数

计算区域各材料分区的参数见表1.塑性混凝土心墙与过渡层接触处设置接触对，切向摩擦系数参考类似工程经验，取为0.2.

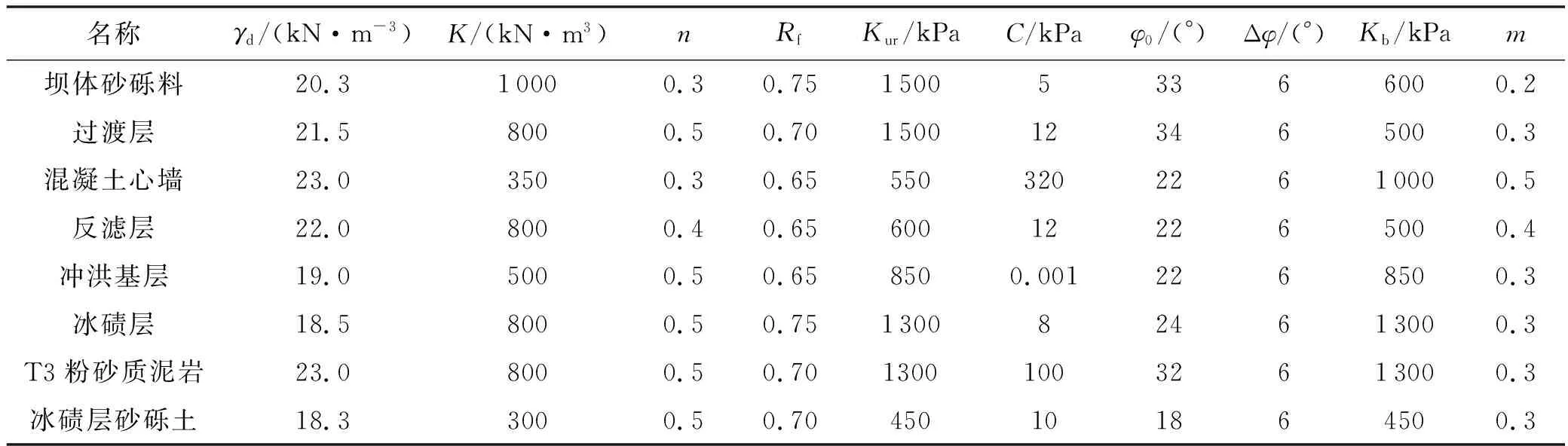
表1 邓肯-张E-B模型材料参数

3.3 计算工况及方案

本次计算主要分析了两个工况下心墙及坝体的应力变形特性.工况1为竣工期，施工填筑共4个加载步，第一个加载步为塑性混凝土心墙的施工，后3个加载步为坝体砂砾石料的填筑施工，按照10 m一个填筑加载步进行加载计算；工况2为运行期，蓄水阶段共1个加载步，该阶段对正常蓄水位以下结点施加静水压力.

考虑到坝址处左右岸的覆盖层厚度差异较大，大坝运行过程中，坝体和塑性混凝土心墙的应力变形可能会展现出明显的差异性.为此，本文特选取河床、左岸岸坡及右岸岸坡3个覆盖层厚度差异较大的断面进行对比分析，以研究覆盖层厚度对坝体和心墙应力变形的影响.

4 计算结果分析

4.1 坝体应力变形分析

上述3个典型断面在各工况下坝体应力变形的最大值见表2.限于篇幅限制，本文只列出河床断面的应力变形云图，如图4～5所示，图中应力规定压为负，拉为正，单位为kPa；位移规定垂直向上为正，水平向下为正，单位为m.

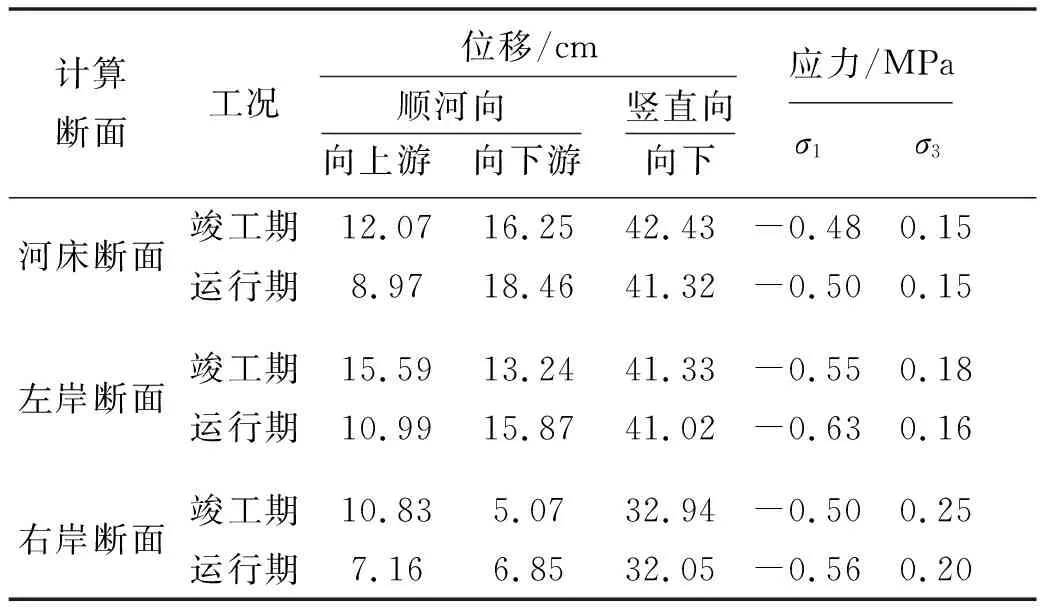
表2 坝体应力及变形最大值结果表

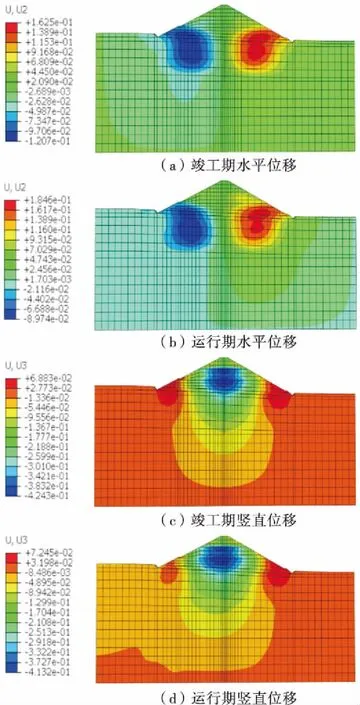
图4 河床断面坝体位移云图(单位：m)

4.1.1 坝体变形分析

从表2和图4可以看出，竣工期河床断面坝体最大沉降量为42.43 cm，约占坝高的1.37%，位于约1/2坝高处；坝体上游填筑区向上游的最大水平位移12.07 cm，下游填筑区向下游的最大水平位移为16.25 cm，均位于坝体底部附近，下游填筑区的水平位移较大主要是由于下游坝坡较陡的缘故.蓄水后，坝体最大沉降量为41.32 cm，比竣工期减少约2.61%，除上下游坡脚处隆起位移略有增加外，大坝整体沉降量减少，产生最大沉降的水平位置明显偏向上游，位于1/2坝高处，符合基本规律；蓄水后的坝体水平位移较竣工期出现了明显的向下游倾斜的趋势，坝体上游坡面向上游最大水平位移为8.97 cm，下游坡面向下游最大水平位移为18.46 cm，位于坝体底部附近.

对比3个断面在各工况下的坝体位移，可以发现右岸断面的坝体水平位移和沉降量要远小于左岸断面和河床断面，坝体沉降量较河床断面减少约22.37%，向上游和向下游的水平位移分别减少约10.27%和68.80%，向上游和向下游的水平位移减少幅度差异较大，主要是由于该断面覆盖层主要分布于坝体上游填筑区，而下游填筑区几乎没有覆盖层分布.由以上结果可见，坝区的覆盖层厚度对于坝体的变形影响较为明显，随着覆盖层厚度的增加，坝体的变形逐渐增大.

坝体变形计算结果表明，由于本工程坝址处的覆盖层较厚且分布不均匀，坝体产生了明显的不均匀变形，且坝体的沉降量较大，超过坝高的1%，这符合以往深覆盖层筑坝的变形实测结果，建议在设计和施工过程中可以考虑对坝基软弱覆盖层进行固结灌浆[11]，以减少坝体的不均匀沉降.

4.1.2 坝体应力分析

从表2和图5可以看出，竣工期河床断面坝体大主应力最大值为-0.48 MPa，位于坝轴线坝基部位，最小值接近于0，位于坝体表面处；坝体小主应力最大值为-0.21 MPa，位于坝轴线两侧接近坝基部位，最小值为0.15 MPa，位于上下游坝体表面附近.蓄水后，由于水压力的作用，坝体大主应力较竣工期有所增加，小主应力最大值略有减少，符合土石坝工程的一般规律.

图5 河床断面坝体应力云图(单位：kPa)

对比3个断面的坝体应力，可以发现各断面的坝体应力值变化较小，且坝内应力分布近似沿高程增加而减少，说明坝体的应力变化主要由自重决定，受覆盖层厚度影响较小.

坝体应力计算结果表明，坝体的拱效应明显，压应力呈现中间大两边小的规律，坝体内土体基本处于受压状态，但在上下游表面处出现了局部拉应力区，但拉应力值较小，应注意做好上下游坝坡处的安全防护工作.

4.2 塑性混凝土心墙应力变形分析

4.2.1 心墙变形分析

图6为各工况下塑性混凝土心墙最大纵剖面的位移云图，图7为各断面心墙上游面顺河向水平位移以及沉降量的沿高程分布图.

图6 心墙位移云图(单位：m)

图7 心墙上游面位移沿高程分布图

从图6可知，竣工期心墙的最大沉降量为71.73 cm，位于左岸坝段坝顶处，最小沉降量位于墙底部位，心墙总体沉降趋势随高程增加而增加；心墙的顺河向水平位移以向下游为主，其最大值为4.41 cm，对应挠跨比为0.08%，位于左岸坝段1/2坝高处.蓄水后，心墙的整体沉降量减少，最大值为69.70 cm，同样位于左岸坝段坝顶处；蓄水后的心墙顺河向水平位移出现了整体向下游倾斜的趋势，最大值为9.68 cm，对应挠跨比为0.18%，位于左岸坝段1/2坝高处.

从图7可知，右岸坝段的心墙顺河向水平位移和沉降量要远小于左岸坝段，竣工期右岸断面心墙沉降量最大值为52.61 cm，较左岸坝段要减少约26.66%；蓄水期右岸断面顺河向水平位移最大值为5.70 cm，较左岸坝段减少约41.12%.由以上结果可知，坝区覆盖层厚度对于塑性混凝土心墙的影响明显，覆盖层越厚，心墙的变形越大.

心墙变形计算结果表明，心墙的挠跨比较小，发生挠曲破坏的可能性不大；但由于坝基防渗墙施工直接与较为软弱的地基接触，心墙内产生了明显的不均匀变形，且左岸坝段的心墙沉降量较大，大坝运行过程中墙体易产生裂缝，但心墙下游设有反滤层过渡层，具有堵塞泥沙，淤填在心墙可能出现的裂缝中，实现自愈防渗的效果，确保了大坝的安全运行.

4.2.2 心墙应力分析

图8为各工况下塑性混凝土心墙最大纵剖面的应力云图，图9为运行期各断面考虑0.2 MPa抗拉强度的心墙上游面大小主应力与静水压力沿高程分布图.

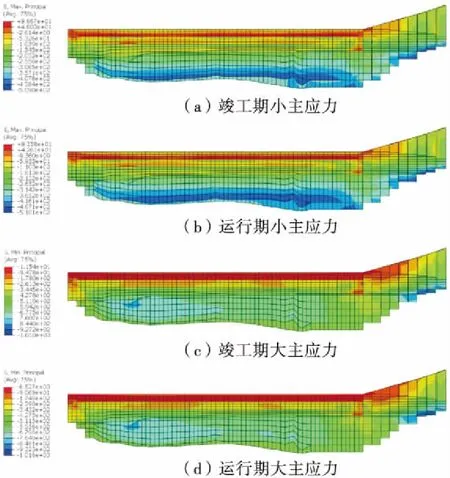
图8 心墙应力云图(单位：kPa)

从图8可知，竣工期心墙小主应力最大值为-0.51 MPa，出现在心墙底部附近，最小值为0.1 MPa，出现在心墙顶部附近；大主应力最大值为-1.01 MPa，出现在右岸坝段心墙底部附近，主要是由于右侧山体突然加高，最小值为-0.01 MPa，出现在坝顶附近.蓄水后，心墙的大主应力有所增加，小主应力有所减小.

从图9可知，各断面心墙的应力变化不大，墙内应力分布都近似沿高程增加而减少，自重效应明显，说明心墙的应力变化主要由自重决定，受覆盖层厚度影响较小.

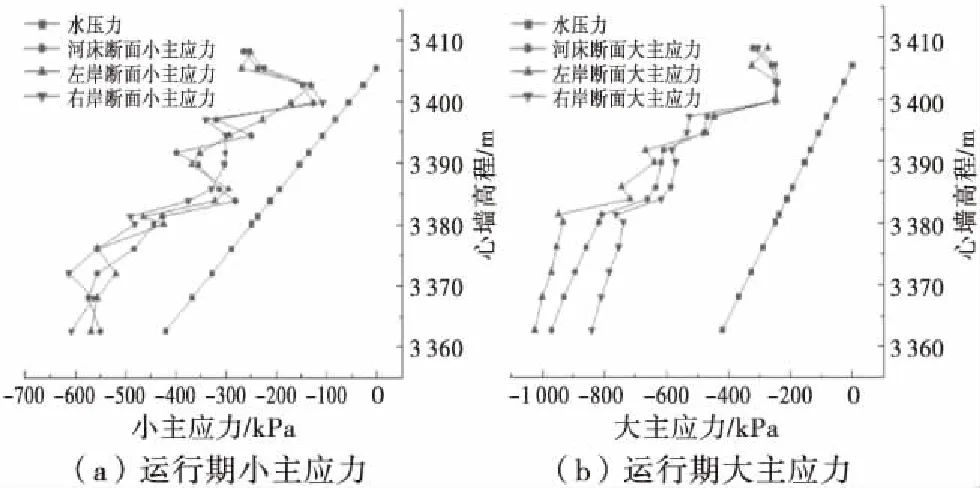
图9 考虑0.2 MPa抗拉强度的心墙上游面应力与静水压力沿高程分布图

心墙的应力计算结果表明，心墙内基本处于受压状态，所受最大压应力值远小与塑性混凝土的抗压强度2.0 MPa，但是心墙顶部附近出现了小范围的拉应力区，但拉应力较小，未超过0.1 MPa.此外，本文采用总应力法对心墙发生水力劈裂的可能性进行了判别，从图9中可知，考虑0.2 MPa抗拉强度的大小主应力均大于相应高程上的静水压力，说明心墙内发生水力劈裂的可能性较小.

5 结 论

本文以云南省某土石坝为例，研究了塑性混凝土心墙坝的应力变形特性，主要得出以下结论：

1)该坝在竣工期和运行期的坝体沉降量较大，最大沉降量达到为42.43 cm，约占坝高的1.37%，同时心墙的沉降量也较大，最大沉降量达到了71.73 cm，与坝体产生了明显的变形不均匀性，这是由坝址处的深厚覆盖层导致的，建议设计施工过程中可以考虑对坝基覆盖层进行固结灌浆，以减少坝体和心墙的沉降和不均匀变形.

2)在竣工期和运行期，坝体和心墙基本处于受压状态，局部存在拉应力区，但拉应力很小，小于土体和塑性混凝土的抗拉强度.为安全起见，应加强对上下游坝坡的安全防护工作，以防发生拉剪破坏.

3)通过对比左岸、右岸以及河床3个断面的坝体和心墙的应力变形，可以发现坝址覆盖层厚度对于坝体和心墙的变形影响较为明显，覆盖层越厚，变形越大；但是坝体和心墙内的应力其主要由自重决定，受覆盖层厚度影响较小.

4)塑性混凝土心墙在竣工期和运行期受力变形状态良好，发生拉剪破坏、挠曲破坏和水力劈裂的可能性较小，大坝防渗系统具有足够的安全性.因此，在该坝址处采用塑性混凝土心墙坝是切实可行的.