《圆锥曲线与方程》教学探究

沈瑜

[摘 要]《圆锥曲线与方程》是解析几何的核心内容，也是高考数学的命题重点.其教学策略有：问题引领，激发兴趣;抓住重点，明确目标;优化算法，提升能力.

[关键词]圆锥曲线;方程;教学

[中图分类号]    G633.6        [文献标识码]    A        [文章编号]    1674-6058（2021）14-0011-02

《圆锥曲线与方程》是解析几何的核心内容，也是高考数学的命题重点.与《直线和圆的方程》相比，它的计算量与难度直线上升.那么，教师如何从教材和学生的实际出发，抓住重点，开展有效的教学活动？本文结合具体的教学实际谈几点认识，供同仁参考.

一、问题引领，激发兴趣

在《圆锥曲线方程》的起始课上，教师可以让学生思考下面三个有趣的问题.

问题1： 据报道，1997年1月，地处南京紫金山天文台发布了一个关于天体运动的消息，从那年2月起，一颗名为海尔·波普的彗星将慢慢靠近地球，而过了4月后，它又将渐渐远离地球.专家预测三千年后，这颗彗星还会与地球擦肩而过.那年的2月至3月期间，许多人有幸目睹了这个三千年一遇的天文奇观.同学们，你知道天文学家是如何预测的吗？

问题2：给你图钉、笔和拉链，请你将拉链拉开一部分，在拉开的两边上各选取一点，分别固定在[F1]、[F2]上，[F1]到[F2]的长为[2a（a>0）].把笔尖放在[M]处，随着拉链逐渐拉开或闭拢，笔尖就画出一条曲线，画出来的这条曲线叫什么？

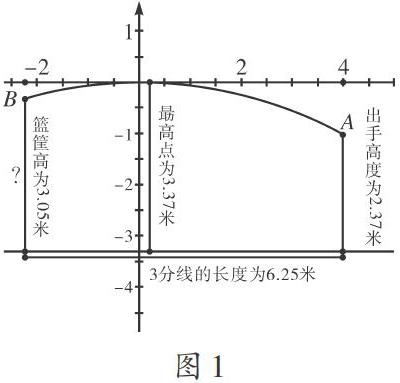
问题3：乔丹，国际篮球巨星.38岁时复出，神勇不减当年.当全场比赛只剩最后一秒的那个瞬间，华盛顿奇才仍落后于纽约尼克斯于2分，关键时刻，巨星在三分线外出手了！（此时乔丹与篮框中心在地面的投影相距6.25米）已知篮球的飞行轨迹是抛物线，乔丹出手高度为2.37米，篮框的高度为3.05米，篮球在飞行了4米（水平距离）后达到最高3.37米（如图1），乔丹此次能否力挽狂澜呢？

上面三个问题，或许学生现在无法回答，但教师可以告诉学生：等学完了本章内容后，相信同学们一定会回答出来.其实，这里我要告诉大家的是上述三个问题分别对应三种曲线：椭圆、双曲线和抛物线，它们统称为圆锥曲线.随着现代科学技术的发展，圆锥曲线的知识和解析几何的思想方法越来越得到社会的重视.今天，在学习平面解析几何初步的基础上学习本章内容，我们将学习椭圆、双曲线和抛物线的方程和几何性质，再次感受幾何问题代数化的神奇与美妙，感受方程思想和数形结合思想在解析几何中的魅力.

二、抓住重点，明确目标

作为教师，必须抓住教学重点，实现教学目标.那么本章教学中教师应抓住哪些重点呢？

1. 要教会学生把握圆锥曲线定义

圆锥曲线有个统一定义，我们如何理解统一定义中体现的椭圆、双曲线和抛物线的共同特征？书本知识是前人的经验总结，只有自己真正理解了才能内化为自己的知识，才能在解题时做到应用自如.圆锥曲线是平面解析几何的重要内容，透彻地理解圆锥曲线定义对本章的学习非常重要.

点评：求曲线的方程首先要研究曲线上动点的几何特征，抓住特征、揭示内涵，特别注意椭圆轨迹定义的应用.

2.要教会学生用数形结合思想分析问题

我国著名数学家华罗庚有首脍炙人口的七言诗：数缺形时少直观，形少数时难入微，数形结合百般好，割裂分家万事休.” 这首诗告诉了我们“数”与“形”各自的特点和不足，从而强调了数形结合的重要性. 因此在解析几何的学习过程中，我们始终都要注意运用数形结合的思想和方法去分析问题、解决问题.

点评：解法一注重代数运算，解题过程十分烦琐，而解法二注重抛物线的定义和图形的几何性质，解题过程简洁明了.

3. 要让学生通过联想与类比发现问题

在学完了圆锥曲线后，教师可以引导学生站在一定的高度整体地看圆锥曲线，看看它们的共同点，探探它们的不同点，运用类比与推理的手段，发现它们相似却不完全一样的有关性质.

所以（1）、（2）两式就是椭圆、双曲线与圆类似的结论.

点评：通过探究，让学生知道，这一结论是有“心”二次曲线的“共同特征”.而抛物线没有中心，所以它没有这种类似的结论.

在圆、椭圆、双曲线、抛物线之间相互类比，是理解圆锥曲线的重要方法.例如，从命题“以抛物线的焦点弦为直径的圆必与抛物线的准线相切”出发，我们可以类比出下面“惊人相似”的两个命题：1.以椭圆焦半径为直径的圆一定与以长轴为直径的圆相内切;2.以双曲线焦半径为直径的圆一定与以实轴为直径的圆相切.

三、优化算法，提升能力

学习《圆锥曲线与方程》的终极目标是提高学生的逻辑推理能力和数学运算素养.我们时常会发现，有的学生面对实际问题虽然能说出解决问题的办法，却算不出结果来.其根本原因就在于选择方法不当或计算不过关.因此，在教学中，我们不仅要培养运算能力，还要重视渗透算法的意识，如设而不求的应用、点差法的应用、如何处理定点定值问题、如何处理最值与取值范围问题等，以提升学生的分析问题与解决问题的能力和数学运算的素养.

（责任编辑 黄桂坚）