“立德树人”视角下高中数学新授课教学模式探究

韦国亮

[摘 要]探究“立德树人”视角下高中数学新授课教学模式，以培养学生一丝不苟、不懈探索、不人云亦云的优秀品质，提高学生的数学学科核心素养.

[关键词]高中数学;立德树人;新授课;教学模式

[中图分类号]    G633.6        [文献标识码]    A        [文章编号]    1674-6058（2021）14-0001-02

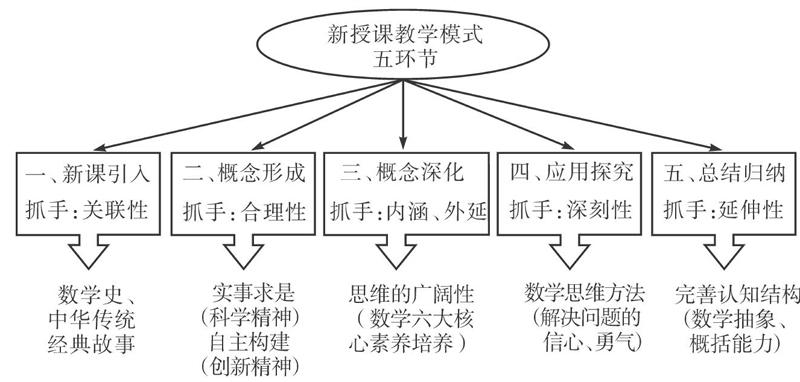
为了全面贯彻党的教育方针，广西南宁市第三中学在数学学科教学模式研究上已取得不错的成果.在首届基础教育国家级教学成果奖评比中，黄河清校长的《高中数学“问题导学”教学法》获得二等奖.黄校长研究的七种课堂教学模式已构建并在学校全面实践.如何在已有的数学教学模式中落实“立德树人”目标，实现学科育人、教学育人？这是目前高中数学教学急需解决的问题.黄河清教学团队对此做了许多探索.笔者作为黄河清教学团队的一员，现以一节教学公开课《方程的根与函数的零点》为例，探究在“问题导学”基础上以“立德树人”为视角的高中数学新授课教学模式.新授课教学模式总结如下.

一、“新课引入”环节，注重融入数学史、中华经典故事内容

“新课引入” 是新授课教学模式的基础环节，“关联性”是这环节的关键之处.黄校长在“问题导学”教学法中指出，成功的教学设计是以“问题”为抓手.科学地设计“问题”，调动学生的学习积极性，引导学生积极思考，培养学生的学习兴趣.设计的问题要注重数学史、中华传统经典故事内容的融合.中华民族有着五千年光辉灿烂的文明史，是一个有数学成就的民族，从《墨经》几何学到《九章算术》等，都是优秀中华数学文化的明珠.数学的发展也体现了全人类探索世界、认识世界的历程和智慧.以数学史、中华传统经典故事内容为切入点，使学生对科学家、对中华优秀传统文化从了解到崇敬，养成忠于科学、忠于事实、忠于中华民族传统的思维习惯，提高学生数学学科核心素养，从而实现“立德树人”的教学目标.

例如，在《方程的根与函数的零点》这节课中，在“新课引入”环节，笔者进行了如下设计.

问题1：请同学们想想有关方程的中国数学历史故事有哪些？

笔者先让学生回答，学生回答后，笔者先引入任正非所说的话：“中国要和美国竞赛，唯有重视数学.”以此激发学生热爱数学、热爱祖国的情感;接着介绍我国古代数学家约公元50～100年编成的《九章算术》，就给出了求一次方程、二次方程根的具体方法，强调这比西方要早三百多年，引发学生的民族自豪感;最后再介绍秦九韶给出了求任意次代数方程的正根的解法，贾宪给出了三次及三次以上的方程的解法，使学生对中华优秀传统文化从了解到崇敬，从而实现“立德树人”的教学目标.

本环节引入中国数学史，深入挖掘教材中丰富的史料及其育人价值，让学生了解数学知识的时代背景和历史条件，及与人类发展的关系.特别是前人在探索过程中所经历的艰辛，所表现出的坚持、拼搏精神，这些德育内容使高中数学课堂达到教学与德育相融的育人效果，达到“立德树人”的目的.

二、“概念形成”环节，注重学生科学精神的培育和创新能力的培养

“概念形成”是一节课的重点，这一环节的关键是概念形成的“合理性”，必须着重强化学生实事求是的精神和探索的精神.数学学科育人强调培养学生拥有求真务实、理智严谨、开拓创新的理性思维.通过数学学科的学习，发展学生坚持公正、忠于科学、一丝不苟、不懈探索、不人云亦云的优秀品质.

如何突出“概念形成”这个重点，达到学科育人的教学目的？笔者在《方程的根与函数的零点》这节课中设计了如下的教学过程.

效能分析：先让学生解几个不同类型的一元二次方程，理解方程根的概念，接着让学生画这几个方程对应函数的图像.图像分为与x轴有1、2个交点和没有交点三种情况，随后教师公布答案.教师通过提问学生，引导学生掌握方程与函数思想、分类讨论思想和数形结合思想，提高学生的数学解题能力.

问题2：函数[f（x）]的图像与x轴的交点和函数对应方程的根有什么关系？

效能分析：给出课堂重点内容之一，即函数的零点概念形成.以问题引导学生在解题中形成概念，这个环节主要问题的设计要注重发挥数学育人的功能，培养学生看问题时注重本质、去粗取精、去伪存真和触类旁通，提高学生抽象概括的能力，引领学生追求真理、实事求是和不断创新，这是数学教师义不容辞的责任.

三、“概念深化”环节，注重多角度、多层次剖析问题，拓展思维

“概念深化”是一节课的灵魂，它能进一步拓宽学生的思维，提高学生的数学学科素养.教师要指导学生学会挖掘概念的内涵和外延，做到透彻理解概念的内涵，熟练掌握概念的应用.

效能分析：通过数形结合思想，让学生掌握“零点”“根”和“交点”三者之间的关系，提高学生解决函数零点问题（高考常见压轴题）的能力.同时也让学生学会深入“思辨”，培养学生在数学学习中不断探索和辨析的精神.

四、“应用探究”环节，注重数学思想方法的理解和融会贯通

本环节的关键是体现思维的深刻性，以“问题链”的方式培养学生的数学思维，增强学生的勇气和信心.笔者以两个问题组成“问题链”进行应用探究.

效能分析：通过问题的设计，既让学生学习了函数的零点定义，又得出了第二个重点内容——零点存在性定理.做到严谨设计，环环相扣，循序渐进，强化思维过程，促进思维品质提升.“应用、探索”是一节课的关键，这一环节要引导学生注重数学思想方法的学习，学会“用数学眼光观察世界，用数学思维思考世界，用数学语言表达世界”.同时，概念的应用可以让学生懂得理论来源于实践，让学生敢于提出问题和解决问题，善于总结和反思，拥有不断追求、探索和解决数学难题的精神.

五、“归纳小结”环节，注重知识结构网络构建，培养学生抽象概括的能力

本环节要注重完善知识结构，在这过程中提高学生的抽象概括能力.

问题6：本节课在数学概念、数学思想和数学方法三个方面你有哪些收获和体会？

这一环节的关键是“构建知识网络”.在本环节中笔者采取师生互动形式，引导学生进行总结归纳，构建本节课的知识网络，效果良好.科学的“总结归纳”非常必要，它可以让這节课的教学效果达到最大化，可以提高学生的逻辑思维能力，培养学生提出问题、发现问题和解决问题的能力.

以“立德树人”为视角构建高中数学新授课的教学模式，要注重结合“问题导学”教学法的思想，以“问题链”方式突破教学难点.同时紧紧围绕“数学学科育人”，紧扣落实数学学科育人目标，在数学教学中以“立德树人”为目标，以“思维、史料、审美、文化、实践”五个维度为抓手，形成“五育”育人模式，对数学教学各环节实施“全覆盖”，全面推进“立德树人”目标深度融入数学课堂，使数学教学从形式到内容彰显 “立德树人”教学目标的引领.

（责任编辑 黄桂坚）