渗透数学思想 培养学生能力

董杰玲

[摘 要]在“找规律”的教学中，创造性地使用教材，初步渗透模型思想、分类思想、函数思想，培养学生自主探究、构建知识网络及推理的能力。

[关键词]找规律;数学思想;能力

[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068（2021）14-0056-02

《义务教育数学课程标准（2011年版）》中，义务教育数学课程的“总目标”表述可概括为：获得“四基”，增强能力，培养科学态度。下面就以人教版教材一年级下册“找规律”的教学为例，论述如何在教学中渗透数学思想，培养学生的能力。

一、初步渗透模型思想，培养学生自主探究的能力。

【教学片段1】

出示（教材第85页例1）：

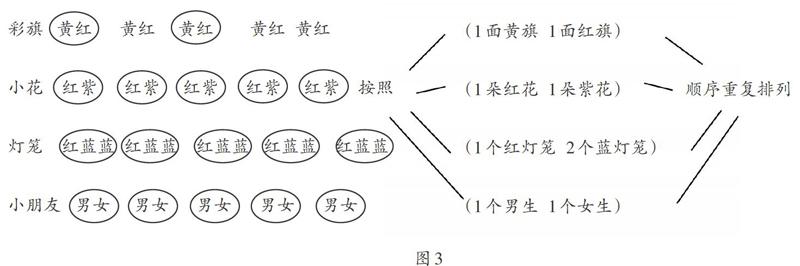
师：观察彩旗、小花、灯笼、小朋友的排列，你发现了什么规律？

本课是“找规律”单元的第一课时 ，例1呈现了彩旗、小花、灯笼、小朋友的排列规律。“规律”有三要素，分別是“元素”“顺序”“组”，在学习本课前，学生已经拥有了探索规律的知识，如数数，1个1个、2个2个、5个5个、10个10个地数;在整理20以内加法表中探索了计算的规律;在认识图形中感受了简单的排列规律;在日常生活中对规律也有许多感性认识，如公园里花盆的排放顺序、马路上的斑马线等。

基于学生已有的知识及经验，此环节的教学分两个层次进行。

第一层次：教师引导

①找规律，圈出重复部分。首先指引学生观察彩旗，重点引导学生思考“谁重复排列了？”“有没有一个好的办法能让人一看就知道是谁重复排列了？”，让学生说出“把重复部分圈起来”，进而得到找规律的方法——圈出重复部分，让学生明白这些规律的“核心”是重复的，并要圈起来。

②描述规律，建立“模型”。彩旗的排列规律是：1面黄旗、1面红旗， 1面黄旗、1面红旗， 1面黄旗、1面红旗……就说彩旗的规律是按照“1面黄旗、1面红旗” 的顺序重复排列的。至此，初步建立描述规律的“模型”—— 按照（     ）顺序重复排列。

板书“模型”（如图2）：

找彩旗的规律是本课的第一个例子，教学时间较长，主要是引导学生明确规律的三要素。“1面黄旗、1面红旗”即是规律中的“元素”，圈起来即是确定了规律的“组”，按照从黄色到红色的顺序排列，这就确定了规律的“顺序”。

第二层次：自主探究

在学生学会利用“圈出重复部分”找到彩旗的规律，用“模型”口头描述规律后，让学生利用所学知识，分小组探索小花、灯笼、小朋友排列的规律，再分组汇报结果。教师最后完善板书“模型”（如图3）：

学生是学习的“主体”，2个层次的教学从教师的“引”到学生的“自主”学习，为学生架起了规律的模型，指明了研究模式，让学生能更直观地进行探究。可见，渗透模型思想，能充分培养学生分析、推理、口头表述、自主探究的能力。

二、初步渗透分类思想，培养学生建构知识网络的能力。

【教学片段2】

出示：

师：小朋友的排列规律除了按照性别来划分，还有没有别的标准？

生：按照“1条裤子、1条裙子”的顺序重复排列。

练习1：在学具盒里找学具，按照自己喜欢的规律摆一摆。

练习2：教材第86页猜规律：

对于例1，学生主要是按照颜色、性别、数量的标准找到彩旗、小花、灯笼、小朋友的排列规律。通过“除了这些标准，还有没有别的？”启发学生可按照“衣服”的标准（1条裤子、1条裙子）来找规律。

对于练习1，学生发现可以按照形状的标准找规律：

图6-1就是按照“1个圆形、1个三角形”的顺序重复排列，图6-2就是按照“1个珠子、2个正方体”的顺序重复排列。也有学生说除了形状以外，也可以按照颜色的标准来找规律，如图6-1就是按照“1个黄色、2个红色”的顺序重复排列……学生发挥自己的创造力，找到了各种各样的标准来创造规律。

对于练习2，学生发现，不仅仅可按照性别“1男、2女”和衣服“1条短裤、2条裙子”的标准，还可以按照动作“上、中、下”和头发长短“1人短发、2人长发”的标准找到规律。有的学生看到上、中、下的动作，马上指出体育课上的口令“一二一 ，一二一 ，一二一……”，这是按照声音、数字标准发现规律。

这样，利用学生熟悉的生活或校园环境的素材，让学生能从颜色、性别、形状、动作、声音、数字等角度和标准找到“规律”。学生从能根据“单一”标准找到规律，到能“从不同角度，按照不同标准”找到规律，从“点状”连成“线状”，形成自己“网状”的“规律”知识结构，完善自己的认知系统。至此，渗透分类思想，培养了学生建构知识网络的能力。

三、初步渗透函数思想，培养学生的推理能力

【教学片段3】

应用规律练习：

1.教材第89页第1题。

划去不符合规律的图形或文字，圈出正确的。

2.教材第85页“做一做”：按照自己喜欢的规律涂色。

根据规律，能找出被遮挡的图形吗？

3.根据规律，接着应该怎样摆？

多种形式的课堂活动，能帮助学生理解规律、应用规律。如上面的练习，让学生把观察和推理相结合，从前一项推出后一项，深化规律的运用，促进学生不断加深对规律的认识和理解。学生从“看到”到“想到”，从“有限”到“无限”，不断丰富对规律的认识，培养了推理能力。

《义务教育数学课程标准（2011年版）》指出“数学教学必须注意从学生的生活情境以及他们感兴趣的事物出发，为他们提供参与的机会，使他们体会到数学就在身边，从而对数学产生亲切感。”本课教学从学生熟悉的人和物出发，让学生感悟规律，理解规律;学生会从颜色、性别、形状、动作、声音、数字等角度找规律，发现规律的“核心”;学生会按照“模型”口头表述规律，会应用规律解决问题。教材上、生活中、校园内都存在“规律”，学生体验到“规律”无处不在，非常亲切，感悟数学就在身边，而数学模型思想、分类思想、函数思想等都蕴含在学生数学知识的形成、发展和应用的过程中。

数学思想是数学教学活动的精髓，有效的课堂就要关注数学思想的渗透和学生能力的培养，从而提高学生的核心素养。

（责编 童 夏）