“阅读与理解”如何做到位?
卢映芬

[摘 要]“阅读与理解”作为小学数学“问题解决”教学的第一个步骤,它承载着培养学生发现问题能力和提出问题能力的重要任务。结合具体课例论述 “阅读与理解”的作用——为学生后续顺利分析问题和解决问题打下坚实的基础。
[关键词]解决问题;阅读与理解;能力培养
[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068(2021)14-0019-03
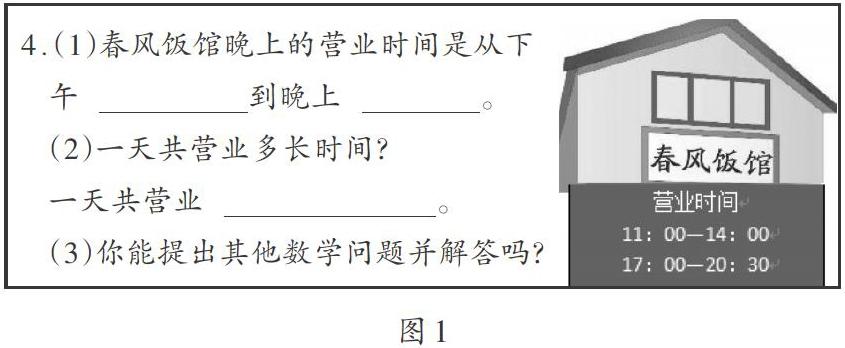
对于三年级下册“计算简单的经过时间”,教材紧密联系生活实际,以解决问题的形式创设了一个“知道出发时刻和到达时刻,求到奶奶家要坐多长时间火车”的实际问题。某教师教学时首先出示解决问题的一般步骤,鼓励学生分析和解答问题;接着呈现学生提出的三种方法,并给予肯定;最后通过比较和分析对三种方法进行优化。该教师教学思路清晰,教学方法恰当,整个新知探究环节很流畅。但对于问题“春风饭店一天共营业多长时间?”,较多学生不能正确解答,他们把11:00看作开始时刻,把20:30看作结束时刻,算出一天营业时间是9小时30分。究其原因,是“阅读与理解”这一环节的作用未发挥到位。下面结合该教师的教学进行逐一分析。
【教学片段】
师:从题目中知道了什么信息?要求什么?
生1:知道春风饭馆的营业时间是中午11:00 —14:00,下午17:00 —20:30。
生2:解问题(1)要将下午的营业时间从24时计时法转化成普通计时法。
生3:问题(2)是求一天共营业多长时间。
生4:题目还让我们提出其他的数学问题并解答。
师:会解决吗?
生(齐):会。
很明显,这一环节除了让学生明确信息和问题外,还必须让他们明确春风饭馆的营业时间分为中午和下午两段时间,一天的营业时间需要分两段计算。虽然学生回答时有提到“春风饭馆的营业时间是中午11:00 —14:00,下午17:00 —20:30”,但这纯粹是按字面宣读而已,学生未必真正理解。对此,教师应该在第一位学生说出春风饭馆的营业时间时插入问题“关于营业时间,还有什么补充吗?”或者直接问“营业时间是从11:00一直到20:30吗?”,让学生在师生问答的过程中认识到春风饭馆是有休息时间的,所以计算“一天共营业多长时间”需要分段计算。实践证明,适时插入问题确实能使学生更好地理解营业时间,避免出现以上错误。
那么,在“问题解决”教学中,解题步骤“阅读与理解”到底承载了哪些任务,如何把“阅读与理解”的作用发挥到位呢?
一、“阅读与理解”实现了生活问题向数学问题的转化
一二年级的“问题解决”将数学知识与生活实际紧密联系,常以情境图的形式呈现题目。这些都需要教师引导学生根据实际情况通过阅读文字或数数等方法发现生活情境中的数学问题,正确获取题目的数学信息并提出问题,将信息和问题完整表述,实现生活问题向数学问题的转化。
【教学片段1】
课件出示:
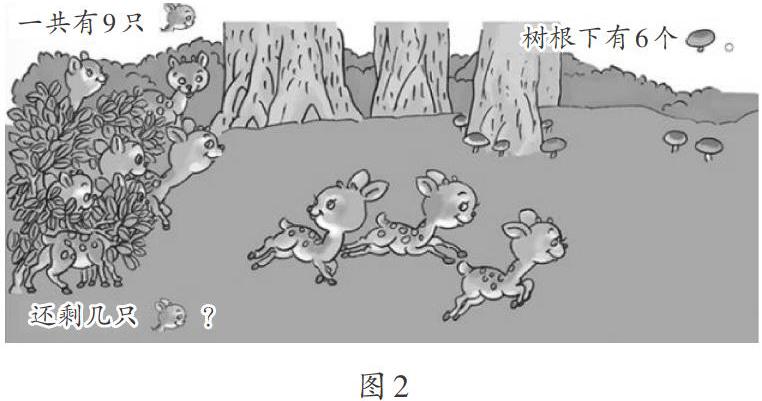
师:关于小鹿,你知道了什么?
生1:一共有9只小鹿,有的站着,有的走了。
师:几只站着,几只走了?请把信息和问题说完整。
生2:一共有9只小鹿,有3只走了,问还剩几只。
师:不错,信息、数量和问题都说完整了。谁能将信息和问题完整地说一次。(学生争先恐后举手)
生3:一共有9只小鹿,走了3只,还剩几只?
师:说得真好!请跟同桌互相说一说。(同桌互说)
教师以一问一答的形式引导学生将已知信息和问题完整表述,让学生充分感悟“问题解决”的两个信息和一个问题的基本结构。
【教学片段2】
课件出示:
师:关于天鹅,你知道了什么?能提出什么问题?
生1:一共有8只天鹅,走了3只,还剩几只?
生2:没有8只天鹅,只有7只。
师:到底是7只还是8只?
生3:题目已经写了“一共有8只天鹅”, 有一只天鹅被水草遮住了,他没看到而已。
师:你观察得真仔细!(指着被遮住的那一只天鹅)这一只天鹅确实是被遮住了,所以“一共有8只天鹅”,没错!如果水草再多一些、密一些,把这一只完全遮住了,那我们要相信自己数出来的只数还是题目中文字表述的8只呢?同桌交流想法。
生4:我觉得还是看题目中写的数。
师:也就是说以文字写出来的数量为准。为什么?
生4:因为有的天鹅可能会被遮住,看不到。
师:你们同意他的说法吗?
生(齐):同意。
师:对,在看图找信息的过程中,可能会出现题目表述的数量和看到的数量不一樣的情况,这时候要以题目文字表述的数量为准。
有了看小鹿图后完整表述题目的引导,学生马上就能学以致用,直接找到天鹅图的两个信息和一个问题,并完整表述。但是新问题出现了——通过数数得到的数量和文字表述的数量不同,怎么办?对此,教师没有急着给出答案,而是让学生通过充分的交流找到解决问题的办法。
【教学片段3】
课件出示:
师:你还能提出什么数学问题?
生1:树根下有6个蘑菇,旁边还有2个,一共有多少个?
师:同意吗?(大部分学生同意)
师(指着树下的蘑菇):明明树下只有5个,怎么说6个呢?
生2:刚才已经说了,如果图上画的数和文字写的不同时,要以文字写的数为准。图上有的蘑菇可能被遮住了。
从解决蘑菇的问题可以看出学生不但能完整表述题目的信息和问题,还深刻认识到当图文表示的数量不一致时,以文字表述为准。这就顺利地将生活中的实际问题转化成数学问题。
二、“阅读与理解”担负着对题目的初步理解的任务
随着年级的递增和知识的深入,中高年级的“问题解决”题目逐渐变得复杂,这时候“阅读与理解”不但要实现生活问题向数学问题的转化,还担负着帮助学生初步理解题目的任务。正如春风饭馆营业时间这道题,在“阅读与理解”这一环节若只是明确题目的信息和问题是远远不够的,还需要学生认真观察营业时间,从中发现营业时间是分两段的。这是在“分析与解答”环节顺利找到这两段营业时间的开始时刻和结束时刻并进行相关计算的关键。其实,从二年级开始,教材就赋予“阅读与理解”初步理解题目的任务。如二年级下册的“用有余数除法解决问题”,在“知道了什么?”这一环节不但要求学生说出已知信息和要求的问题,还需要学生理解关键词语“最多”和“至少”的含义。
【教学片段】
课件出示:
师: 从题中知道了什么?
生1:知道了两个信息——22个学生去划船和每条船最多坐4人。问题是“他们至少要租多少条船?”。
师:也就是知道了划船的人数是22人。“最多坐4人”是什么意思?
生2:最多坐4人就是不能超过4人。
师:那坐1人可以吗?坐2人、3人呢?
生2:可以。
师:还有哪些词需要注意的?
生3: “至少”这个词。
师:“至少要租多少条船?”该怎么理解?
生3:就是说要租的船不能太多,船的只数要最少。
师:1人坐一条船怎么样?2人呢?3人呢?
生4:不行,这样要租的船就多了。
在学生初步理解题目后,教师还可以列举生活中的例子加深学生对词语“最多”和“至少”的理解,同时培养学生审题的习惯与理解问题的能力,为学生在“怎样解答?”环节中用画图法分析问题并解决问题做鋪垫。
三、“阅读与理解”担负着对空间关系(数量关系)初步分析的任务
如五年级下册第70页例3(公倍数、最小公倍数在生活中的实际应用):
在“阅读与理解”这个环节,教师需要引导学生完成以下三个任务:一是引导学生读题,通过对关键数据和词语的理解明确题意;二是让学生通过画图初步理解题意,感受铺出的正方形的不确定性;三是让学生综合信息,厘清思路,抓住问题解决的关键:满足要求的正方形受墙砖长和宽的限制,可以应用公倍数和最小公倍数的知识解决问题。这三个任务不但将铺砖这样的生活问题转化成数学问题,同时也为“分析与解答”环节确定“要求铺成的正方形的边长可能是多少分米就是求3和2的公倍数是多少”的解题策略做好了铺垫,为利用画图策略来检验解答是否正确打下了坚实的基础。
【教学片段】
师(课件出示图6):题目讲了什么?
生1:用长方形的墙砖铺一个正方形。
师:有什么需要特别注意的吗?
生1:用的墙砖必须是整块的。
师:能找出相应信息的数据和问题吗?
生2:能。用长3分米、宽2分米的墙砖铺成一个正方形。问题是铺成的正方形的边长可能是多少分米?最小是多少分米?
师:请先在头脑里想象一下铺砖的画面,再用画图的方法把它表示出来。你有什么新的发现?
生3:铺成的正方形不止一个,可能有很多个。
生4:最小的正方形我已经找到了。最小的正方形边长是6分米。
师:你们同意吗?(学生表示同意)边长除了是6分米,还有可能是几分米?(学生纷纷猜测)
师:老师给每组同学都准备了一套学具,请动手摆一摆,验证猜测是否正确。
古希腊著名的哲学家柏拉图说:“良好的开端,等于成功的一半。”“阅读与理解”是“问题解决”教学中的第一个步骤,也是解决问题的开始。教师必须明确这个环节的任务,并根据学生的年龄特点,结合要解决的实际问题和不同学段的要求对学生进行引导,充分发挥“阅读与理解”这一环节的作用,培养学生良好的审题习惯。
(责编 金 铃)

