沿着学生的思路才能以学定教
孙雪梅


[摘 要]关于“小数乘以整数”的计算法则,多数教师教学时都是直言相告——直接按照整数乘法计算出整数积,再来清点小数位数,学生只是言听计从。教师应解释清楚为何一定要先按整数乘法法则算出整数积,从而体现这种转化的必要性和培养学生主动思考的能力。
[关键词]小数;整数;位数;乘积
[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068(2021)14-0058-02
苏教版教材五年级上册“小数乘以整数”的相关例题包含列竖式、演算、确定小数位数,同时给出两种预设:一是将3个0.8连加;二是把0.8元换算成8角,把因数从小数转换为整数。通过前测发现,学生在探究0.8×3的运算方法时,一律是先算出8×3=24,再将整数积24加上小数点改写成2.4,但让他们说理由时,他们都说不出个子丑寅卯来。即使换算货币单位,化元币为角币,一旦抛离情境,学生还是不知所谓。
一、突出重点才能突破难点
对于积的小数位数和乘数小数位数的关系,学生往往弄不清其中的关联,误以为只要将小数点对齐即可。有的教师建议从积的变化规律来解释,但此时学生尚未学习小数点移动带来分倍率的变化,更何况,如果用因数与积的变化规律来解释积中小数点位置的确定,更不能说清为何要化为整数。
将小数乘法暂时当作整数求积,是教师的“死命令”,如何将其变为学生的“刚需”?对此,笔者重新确定教学重点“一是让学生理解将因数暂时当作整数求积的原因;二是引导学生发现积和因数的小数位数之间的关系。”,并将这两个重点安插在小数乘整数的口算,因为竖式会干扰学生的思考。
为了突出第一个教学重点,笔者从计数单位的角度来揭示算理。这样,学生在口算小数乘整数时,就能自动变换成乘0.1、0.01、0.001等形式来计算,若要如此,必先抽离出整数,先算出有多少个0.1、0.01、0.001。此时,整数乘以整数就是顺理成章的事。然后,通过一组小数乘整数的口算题,先探究后验证,引导学生发现小数位数的前后联系,让学生吃透本质。至于竖式的计算,有了之前发现的规律,竖式就简单得多,先看成整数乘整数是再自然不过的事。这时积的小数位数的确定对学生来说也不再是难题。
二、教学实录
师:今天我们学习的内容是整数乘小数。(出示图1)黑色长条用小数如何表示?
生1:0.1。把矩形视为单位“1”,将其等分为10份,取其中1份染黑就是1/10,也就是0.1。
师(出示图2):取其中4份染黑呢?
生2:是0.4,把矩形视为单位“1”,将其等分成10份,4份就是它的4/10,化为小数也就是0.4。
师:0.4里含有多少个0.1?
生3:4个。
师:4个0.1是多少,列式怎么表示?
生4:0.1×4=0.4。
师(出示图3):黑色部分用哪个小数来表示?说出你的思路。
生5:0.04。把矩形视为单位“1”,将其等分成100份,取其中4份染黑就是它的[4100],写成小数就是0.04。
师:那0.04里含有多少个0.01?列乘法算式如何表示?
生5:4个0.01。0.01×4=0.04。
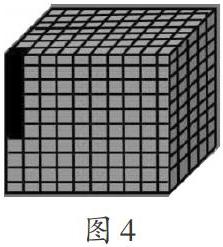
师 (出示图4) :着色的小方块用哪个小数表示?理由是什么?
生6:0.006。把立方体视为单位“1”,将其等分成1000小块,1小块就是它的[11000],写成小数就是0.001,着色的是6个小块,也就是6个0.001,所以是0.006。
师:6个0.001是多少,如何列式表示?
生7:0.001×6=0.006。
师:以上计算中的小数都有什么特征?
生8:都是0.1、0.01、0.001与整数相乘。
师:只要乘以0.1,积就是几位小数?乘以0.01、0.001呢?
生9:只要是整数乘以0.1,结果就有若干个0.1,积只有一位小数……
师:计算0.2×3,0.02×3,0.002×3。如果换成其他小数,又该怎么办呢? 0.2×3的积是多少?
生10:0.2×3=0.1×2×3=2×3×0.1=6×0.1=0.6。
师:先转化为刚刚学过的乘以0.1的算式,结果里共有多少个0.1?积是几位小数?我们用图5来验证。
师:又该怎么算0.02×3的积?
生11:0.02×3=0.01×2×3=2×3×0.01=6×0.01=0.06。
师:真不简单!为何这次是0.01而不是0.1呢?
生12:因為乘数不一样,0.2是一位小数,0.02是两位小数。
师:此时共有多少个0.01?是几位小数?我们用图6来验证。
师:0.002×3的积又该怎么算?
生13:0.002×3=0.001×2×3=2×3×0.001=0.006。
师:小数又转化成小数单位0.001了,此时为何不再是0.1、0.01?
生14:因为0.002是三位小数。
师:你们能够根据不同的小数选择不同的小数单位。我们一起看图7,这时一共有多少个0.001?
师:计算这些题目时,大家都不约而同地将小数转化成了一个整数乘以0.1、0.01、0.001的形式,都是先算——
生15:2×3。
生16:都是先把小数乘整数转化成整数乘整数。
师:整数因数都是3,为什么积的小数位数却各不相同?因为小数因数0.6、0.06、0.006的小数数位也各不相同。
生17:转化而成的小数单位也不尽相同,分别是0.1、0.01、0.001。
师:是什么决定转化的小数单位是0.1,或者0.01,或者0.001?
生18:小数因数的小数位数。
师:看来积的小数位数与因数的小数位数有着千丝万缕的关系,是什么关系呢?
生19:小数因数有几位小数,积就有几位小数。
师:这个规律是不是具有普遍性?真相如何,还需验证。有没有反例?
生20:我认为没有。一位小数乘整数,结果含有若干个0.1,积必然是一位小数,两位小数、三位小数也是如此。
师:如果换成较大的小数,你们会算吗?例如6.35×12。显然,只有尝试列竖式计算了。
师(出示两种不同的做法):你们赞同哪一种?理由是什么?计算过程中出现小数点,合适吗?
生21:不合适,计算过程中不要出现小数点。因为先要将因数当作整数做乘法,最后由小数因数中的小数位数来确定积的小数位数。
三、课后反思
课后调研显示,教学效果令人满意。沿着学生的思路以学定教,学生不但学会小数乘整数的计算法则,并且领悟其精髓。主要体现在以下两方面:
一是从计数单位入手,解析算法、渗透算理。小数乘法的计算必先转化为整数乘法,如何将这其中的深意和原理变成学生的必然思维?笔者认为,采用“换零钱”的办法将用小数表示的元币化为用整数表示的角币实为不妥。因为学生会对这个情境产生依赖,一旦脱离这个情境,学生的认知就会打回原形。而从计数单位入手,就可以摆脱情境的局限性,计算时一律转化成×0.1、×0.01、×0.001……一旦转化成乘以小数单位的形式,先算整数乘整数就是必然发生的事情。同时,整数乘以整数后的积,正好是0.1、0.01、0.001……的个数。
二是突破常规教学,让学生自主尝试,将类比推理和演绎推理完美结合起来。尽管小学阶段不要求学生会证明,但是不代表学生不能论证结论,这就需要教师有魄力和胆略。许多教师只让学生机械记住“因数中是几位小数,积就是几位小数”,没有追根溯源。筆者在学生计算了三道较小的小数乘整数题目后,让学生从形式上观察和归纳因数的小数位数与积的小数位数的关系,然后通过类比来推理出算法,再通过演绎推理出这种规律的普遍性,让学生通过交流、争论,总结出“一位小数乘整数的结果含有若干个0.1,积自然是一位小数;两位小数乘整数的结果含有若干个0.01,积自然是两位小数;三位小数乘整数的结果含有若干个0.001,积自然是三位小数”,至此,学生领悟算理。
(责编 童 夏)

