“知识输入”+“理念创新”=“数学发展”
丁红琴
[摘 要]小学数学教育以“基本技能”训练为主,学生的数学基本功扎实,但创造能力和动手能力严重不足。在小学数学教学中,教师应统筹兼顾学生的实际和新形势的要求,倡导“大道至简”和“取舍有道”,促使学生在坚实的根基上获得数学学习能力和核心素养的发展。
[关键词]板块;全局;取舍;拿来;自创;境界;智慧
[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068(2021)14-0050-02
“在花岗岩地基上建造茅草屋”和“在松软泥土上盖写字楼”的教育观念是失衡的,在小学数学课堂教学中,教师应统筹兼顾学生的实际和新形势的要求,循序渐进地设计教学,促使学生在坚实的根基上获得数学学习能力和核心素养的发展。本文以苏教版教材三年级下册“面积和面积单位”一课为例进行探讨。
一、大道至简:于“板块”中管窥全局
数学教学要彰显学科本色,教学设计要以简洁的线索、形式分明的板块呈现数学本质。各版块的数学知识有着千丝万缕的联系,教师要精研教材,对知识核心和网络洞若观火,铸造数学知识的“板块结构”,并沿着板块脉络来施教,使得课堂简洁有力、从容大气。
“面积和面积单位”这节课,知识点繁多,素材丰实,操作活动缤纷多彩。鉴于此,笔者精心设计了三个教学板块:一是“何为面积”;二是“如何比较面积”;三是“比较面积大小的度量标准”。各个教学板块的重心和思维级别有差异,其中,第一板块主要依赖活动,通过“观察”“触摸”“涂鸦”“画图”,使学生慢慢领悟面积的含义。第二板块主要依仗思考推导结论,笔者删减了教材中提出的比较若干个不同图形的面积的操作过程,借助让3组形态各异的图形“一决大小”,充分调动学生的脑力,探索出比较面积大小的有效途径:观察—重叠—数方格,从而使学生深入领会统一比较标准的重要性。第三板块则纯粹是体验联想的舞台,通过观察实物感知三种面积单位的“分量”,建立敏锐量感。
如此一来,以上三个板块之间的内在逻辑关联一览无余,能帮助学生进行理性思考,对知识的前后融通也是大有裨益的。暴露知识起源,推进脉络,披露隐情,展露了课堂教学的延续性和完整性,促进了学问和技巧、内涵与方法、操作与经验的均衡发展,这样的板块设计崇尚一个原则——大道至简。
二、取舍有道:拿来后仍需自创一格
取,需要勇毅;舍,更需果决。舍得舍得,有舍才有得。自课改以来,对于“被动灌输”和“主动求索”两种学习模式一直未有定论,基本共识是:两者各有千秋,优劣均沾。一线教师应清醒地意识到“模仿、记忆”的固本功能和“主动、探求”的开拓功能,辩证看待,确认它们为互联共存关系。课堂教学中,教师根据知识门类、学生起点、阶段目标等客观情况,将两种学习方式熔为一炉,果断舍弃不合宜、低效的细枝末节,可让学生的学习直达目标。
小学数学概念教学,重在感知内涵,萃取本质。理解和掌握起来,是以学生明确其有大小之别、认为可比大小、做到会比大小为考查验收标准,而不是用学生记住面积定义来衡量。因此,教师应采用“被动灌输”学习和“研究型”学习的混合动力模式,在学生初步感知面积概念的基础上,激发学生自主探究、深入挖掘的欲望,以期探查出精准、明晰、完善的概念。在“何为面积”板块中,笔者创设了4个梯级开展教学。
第一梯级是教师举例,学生分析、判断。
师:老师的手掌与你的手掌,哪个面积大?
[意图:让学生通过是“观察”和“触摸”,体会物体的面,初步感知面積是什么。]
第二个梯级是由学生举例并分析判断。
师:我身边许多物体都有面,如火柴盒、地板砖……这些物体的面都是有大小之别的,具有可比性。谁能描述一下什么是面积?
[意图:让学生自己举例叙述、比较,提炼面积的概念。]
第三个梯级是让学生在判断大小后,认清其倍数关系。
师:一张大油画的面积是一张邮票面积的几倍?
[意图:让学生认清面积大小具有可比性,做出“定性”分析(孰大孰小)和“定量”研判(大多少?或几倍?)两种裁定。]
第四梯级是学生“涂鸦”和“画图”。
师:你能设法画出两个面积不等的闭合图形吗?
[意图:使学生真切体会到闭合图形的面积的大小。]
在以上四个教学梯度中,学生边汲取现成的知识、边创造未知的知识,对“面积”的认识摆脱经验主义和肤浅浮华的束缚,逐步上升到学科专业与理性认识的档次。
三、至高境界:方法技能中提取高级智慧
数学思想方法是从长期的历练和磨砺中提取的科学精华,是将低级、具体的知识加工转型为抽象、高级的观念,是数学教学的最高境界。教师应不遗余力地追求这种至高境界,重视思想方法的渗透。因为学生一旦掌握数学思想方法,就能触及数学的灵魂,并能指导一切学习行为,让学生具备一定的思辨能力。
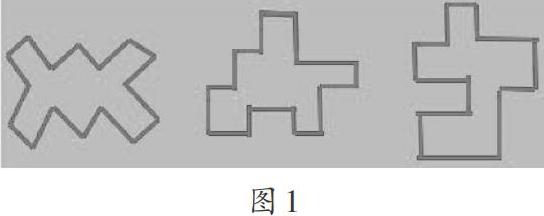
在“如何比较面积”板块中,笔者出示图形(如图1)。
引导学生思考:上述三个图形,哪个图形的面积最大?用观察或重叠的方法进行比较方便吗?为什么?怎么改进好呢?能否找到一种方法,一次性比较出三个图形的面积大小?引导学生利用小方格将这三个图形的面积度量出来,用占据小方格的数量,也就是三个自然数的大小来忠实反映面积大小。这样做,既培养了学生的创新思维,也使学生体悟到:“小方格魅力无穷!它能帮我们把图形问题转化成数数问题,以数字代替形状,数形结合,简化问题。”把几个图形的面积大小统一转译为数字大小,体现了“数形结合”和“化归”的数学思想方法。
学生掌握一定的数学知识和方法之后,需要教师因地制宜,整理反思方法、提炼思想,用精炼的语言指向数学本质,引发学生深思,促进学生融会贯通、大彻大悟,这样的语言称之为“偈语”。本节课的“偈语”有4处:1.观察、触摸、画图、涂鸦,揭开面积的神秘面纱,我们从物体走向图形;2.用观察、重叠、数小方格的方法比较面积大小,我们从粗浅走向了精深。用“数”的大小代替“形”的大小,我们从繁复走向简约;3.比较,需要制定统一度量衡,方显公平公正。比较长度有长度单位,比较面积也需要有面积单位。最后,全课总结:我们从物体的表面到几何图形,结识了面积,为计量面积又规定了面积单位。我们完成了从物体,到图形,再到几何量(图形可量化的形体特征)的奇幻之旅。
总之,数学“基本技能”教学要继承和发扬,需要一线教师不断整合资源,设计“板块”结构,让学生在操作中,掌握数学知识和技能,感悟数学思想方法,形成数学学科素养。
[本文系盐城市教育科学“十三五”规划立项课题“基于小学数学实践活动的生本课堂探索和研究”(编号:2017-L-04)的阶段性研究成果。]
(责编 黄春香)

