关于三次多项式数列的连续多项式分解

杨永刚

（南充市高坪中学，四川 南充 637100）

如果数列通项an是关于自然数n的多项式，则称数列an是多项式数列.多项式数列连续分解的概念由文[1]首先提出，并指出了这种分解的重要意义，而文[1]提出这一概念是基于文[2]中一习道及其解答[3].由于一般情况的复杂性，文[1]只对二次多项式数列和两类特殊的四次多项式数列作了具体研究，并得出了相应结果，而对于三次多项式数列的连续分解仅提到，并未作具体研究.本文采用文[1]的方法，对三次多项式数列的连续分解进行研究，并对三类特殊的三次多项式数列给出具体的连续分解性，最后再指出其在求倒数和与一类特殊求商问题中的应用.

定义1[1]对于数列an，若存在数列bn，使an=bnbn+1…bn+k-1（k≥2），则称bnbn+1…bn+k-1是数列an的一个k阶连续分解.

定义2对于多项式数列an，若存在多项式数列bn，使an=bnbn+1…bn+k-1（k≥2），则称bnbn+1…bn+k-1是多项式数列an的一个k阶连续多项式分解，此时也称多项式数列an可做k阶连续多项式分解.

显然，多项式数列an的一个k阶连续多项式分解也是数列an的一个k阶连续分解.

定理1若三次多项式数列an能作k阶连续多项式分解：an=bnbn+1…bn+k-1（k≥2），则k=3，且bn是一次多项式.

证明：设an=an3+bn2+cn+d（a≠0），则bn不是常数.因为如果bn=h为常数，则bn=bn+1=…=bn+k-1=h，从而an=bnbn+1…bn+k-1=hk为常数，这与an是三次多项式数列相矛盾.设bn=f(n)是关于n的m(≥1)次多项式：

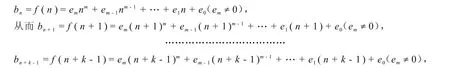
即bn+1,…,bn+k-1也都是关于n的m次多项式，an=bnbn+1…bn+k-1的右边是关于关于n的km次多项式，而左边是关于n的3次多项式，故3=km，由k≥2，且3是素数，故k=3，m=1，即bn是一次多项式.

定理2三次多项式数列an=(an+b)3+c（a≠0）不能作三阶连续多项式分解.

证明：假设an能作三阶连续多项式分解，则由定理1可设

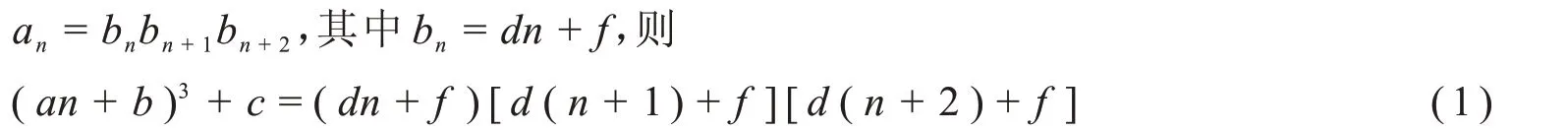
将（1）两边展开并整理为关于n的降幂形式得

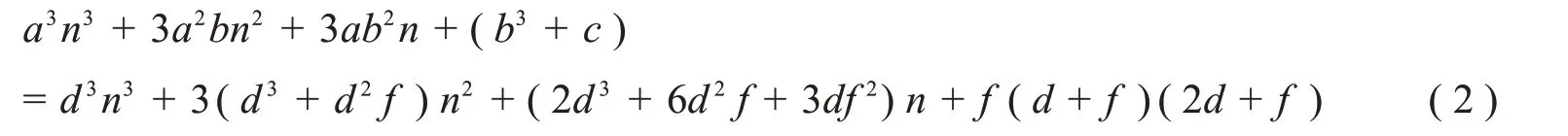
比较（2）式两边的对应系数得

由（3）得d=a，代入（4）解得f=b-a；将d,f代入（5）并化简变形得a=0，这与a≠0相矛盾，故an不能作三阶连续多项式分解.

定理3形如an=an3+bn+c（a≠0）的三次多项式数列能作三阶连续多项式分解的充要条件是：a+b=0且c=0.

证明：（必要性）设an=bnbn+1bn+2，其中bn=dn+e，则

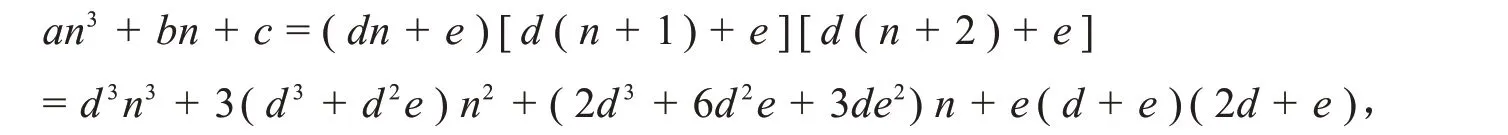
比较系数得：

（充分性）由a+b=0且c=0，则

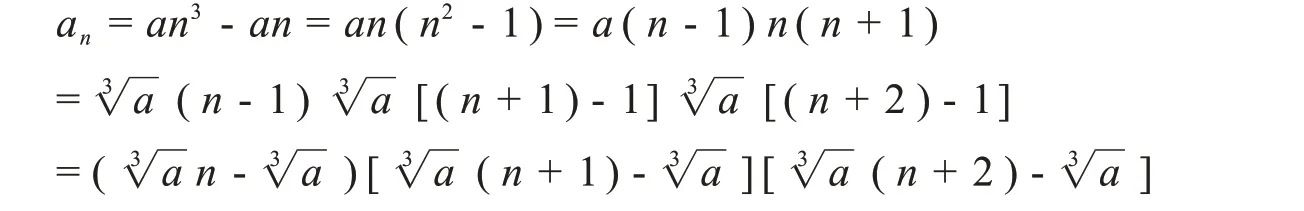
定理4形如an=an3+bn2+c（a≠0）的三次多项式数列能作三阶连续多项式分解的充要条件是：b2=3a2且

证明：（必要性）设an=bnbn+1bn+2，其中bn=dn+e，则

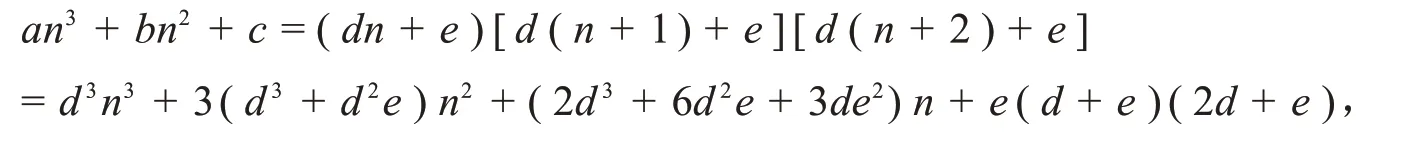
比较系数得：

（充分性）由a、b、c满足则容易验证（11）～（14）都成立，故有下式成立：

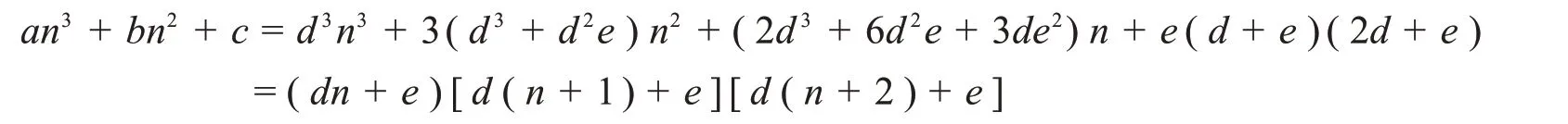
由定理4的充分性的证明立即得下面的定理5.

定理5若三次多项式数列an=an3+bn2+c（a≠0）满足：b2=3a2且，则an=bnbn+1bn+2，其中

最后，如果三次多项式数列an(≠0,∀n∈N*)能作三阶连续多项式分解an=bnbn+1bn+2，其中bn=dn+e是公差为d的等差数列，显然d≠0，bn≠0(∀n∈N*)，从而可以求如下倒数和与商：