轴套工艺尺寸链的数字化算法分析

李进东

（四川职业技术学院 机械工程系，四川 遂宁 629000）

计算机数字化设计不仅在机械产品设计中广泛运用，同时在机械加工中，计算机辅助工艺设计（CAPP）中[1]，也在不断发展和完善。而计算机辅助工艺设计（CAPP）技术，不仅需要对机械产品工艺流程方案的设计，而且还需要对工序尺寸及工序尺寸公差的计算和确定。而工序尺寸及工序尺寸公差的计算和确定是一个相对复杂，费时及容易出错的环节。釆用传统的计算方法，尺寸链建立烦杂，计算参数较多，计算量较大等，因此工作效率较低。如果利用LU计算方法及计算机辅助工艺设计（CAPP）的理论，用计算机求解，不仅可以提高效率，而且更容易实现工艺的自动化设计。

1 工艺尺寸链的数字化算法

计算机辅助工艺尺寸链的分析与解算一直是CAPP中一个倍受瞩目的课题。鉴于此，本文对计算机辅助工序尺寸的解算算法进行了的探讨，首先，基于尺寸链原理,分析了工艺尺寸的解算过程,其次，引入矩阵方程,采用Microsoft Visual C++6.0语言编写计算机程序,解决了与机械加工过程有关的尺寸及公差计算机解算问题,进一步提高了尺寸链的解算速度和质量。

2 零件的加工工艺

某零件如图1所示，零件的加工工艺规程的编制取决于加工工艺能力和加工成本[2]。根据某工厂机床设备及加工工艺能力确定该零件加工工艺，如表1所示。

图1 零件图

表1 轴套机械加工工艺流程

3 工艺尺寸联系图的设计

按照上述加工工艺可得到的工序尺寸有A1、A2、A3、A4、A5、A6、A7、R。工序加工余量为Z4、Z5、Z6、Z7。工艺尺寸联系图，如表2所示，图中标注出各工序尺寸、加工余量、定位及测量基准。

表2 工艺尺寸联系、工序尺寸、加工余量、定位及测量基准表

4 建立尺寸链关系

按照机械加工工艺规程的制定原则，工序尺寸及工序尺寸公差采取单向入体标注，及平均尺寸及公差上下偏差对称分布[3]。建立尺寸链关系如图2所示。

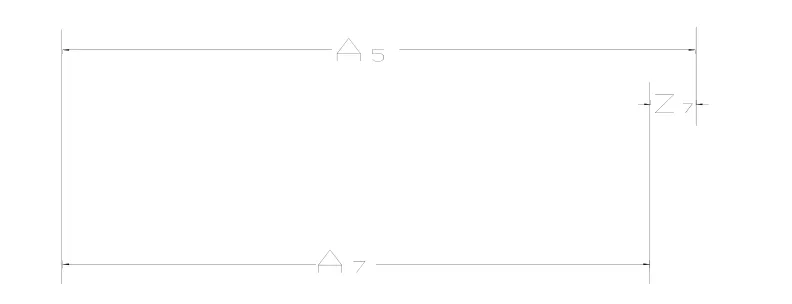
图2 尺寸链关系尺寸链

5 LU计算机算法

根据LU计算机算法，对被加工零件工艺尺寸链的数字化算法进行分析探讨。依据矩阵理论，假如有方程组[4]：

根据矩阵运算，把数矩阵A进行分解，其一，下三角矩阵L，其二，上三角矩阵U的乘积。可得:

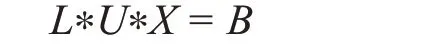
式中：

令UX=Y:

那么将方程（1）分解为两个方程组：

由方程式（2）求解Y，由方程（3）式求解X。

由矩阵乘法原理，可求解出L、U。

由系数矩阵LU=A，可知：

按照矩阵运算，左边乘积的第一列为：

故：

同理左边乘积的第一行为：

故有：

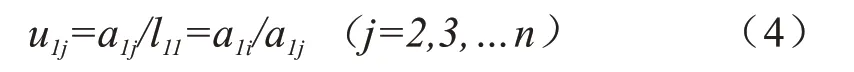
如果以L的第i行乘以U的第j列（i≥j）得：

故：

同理以L的第i列乘以U的第j行（i＜j）得：

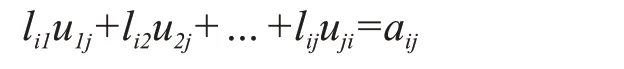
故：

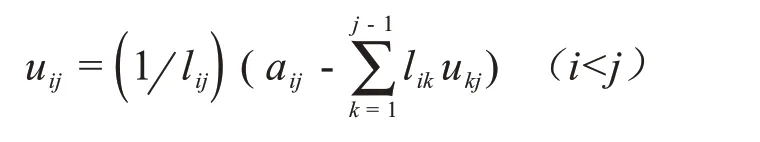
这样可以求得了L及U矩阵。

6 尺寸链的矩阵及线性方程组建立

根据工序尺寸联系图和LU算法理论来建立尺寸的联系矩阵J及尺寸链矩阵K。再列出含工序尺寸、加工余量的尺寸链的线性方程组[5]。在计算机中以矩阵的形式储存工序尺寸的信息，编制程序求解。

建立工序尺寸的联系矩阵J，由表3得出该矩阵得参数。

表3 工序尺寸联系矩阵参数

工序尺寸的联系矩阵J如式（6）。

建立工序尺寸链矩阵K,要求K矩阵的列数与工序尺寸的个数相同，K的行数等于联系矩阵J的行数，这样得到一个矩阵。

工序尺寸链矩阵K的参数为：各工序尺寸链为一行，其参数确定是增环取1，减环取-1，不包括的尺寸项取0。K阵如式（7）。

建立工序尺寸的线性方程组列出矩阵方程如下式（8）。式中分别表示A1、…、A7列，第四行开始 以Z4、Z5、Z6、Z7、R表示。A6=27.07mm、A7=6mm、Z4=1.63mm、Z5=0.48mm、Z6=0.75mm、Z7=0.26mm、R=31.69mm为已知参数。

7 LU分解法编程

用Microsoft Visual C++6.0语言编写[6]求解上述矩阵方程。令X1=A1、X2=A2、X3=A3、X4=A4、X5=A5；B1=Z4、B2=Z5、B3=Z6-A6、B4=Z7+A7、B5=R。则得矩阵方程（9）：

输入已知数值，结果打印如下：

8 结语

数字化设计与制造是智能制造的重要组成部分，其中计算机辅助设计及数控制造技术比较成熟，得到了广泛应用。而机械加工工艺的计算机辅助设计（CAPP），面临工艺过程中的工艺尺寸链求解，零件材料，热处理工艺等诸多不确定性，还在不断发展中。本文对轴套类零件工艺尺寸链应用矩阵理论算法在计算机上进行求解，这种方法实用、高效、不易出错，利于推广及应用，为轴套类零件工艺计算机辅助设计中的工序尺寸链的求解提供了数字计算方法。