基于FP-Growth算法的高校学生公共课成绩与专业课成绩相关性研究

余弦，周谊芬

（南通大学a.杏林学院，b.医学院，江苏 南通 226000）

高校人才培养方案中所计划开设的课程，一般可分为公共课（包含公共选修课和公共必修课）和专业课（包含专业基础课和专业课）两种[1]。一般而言，公共课和专业课之间有一定的相关性，公共课所学习的内容在一定程度上是专业课内容的基础，熟悉公共课知识对掌握专业课内容具有促进作用[2]，但是否每一门公共课的成绩都会对相关专业课的成绩产生影响，以及会产生多大的影响，仍有待研究和验证。

随着信息技术的快速发展，数据挖掘及相关技术在高校的教学、科研等领域得到不断拓展应用。数据挖掘技术在寻找海量数据的内在关联规则方面具有效率高、适用灵活等优点。在教学过程中累积的学生成绩已经形成一个体量庞大的数据库，通过数据挖掘的相关算法来寻找大量学生成绩数据之间潜在的关联规律，进而提高高校课程设置合理性和学生学习效率，已经成为高等教育管理领域的研究热点之一[3]。应用FPGrowth算法对某高校部分计算机专业学生的公共课成绩和专业课成绩进行相关性分析，针对二者的关联程度展开实证研究，为高校教学计划的课程设置和教学改革提供有力的科学依据。

1 FP-Growth算法原理和实现

FP-Growth(Frequent Pattern Tree,频繁模式树)算法是一种在经典Apriori算法基础上演变而来的挖掘频繁项集方法[4]。它针对Apriori算法运行效率较低，实现过程中需要多次扫描整个事务集，进而产生大量候选集的缺点做了明显的改进。FP-Growth算法比Apriori算法效率更高，它将数据集存储于一个按特定顺序构成的树结构（FP树），通过构建FP树来压缩事务数据库中的信息，从而更加有效地产生频繁项集[5]。在整个算法执行过程中，只需遍历事务集两次，通过递归调用FP树结构，删除不符合最小支持度（关联度低）的项目，直至最终形成单一的树结构，就能够完成频繁模式的发现。其发现频繁项集的基本过程如下。

将事务数据库中的单个事务记为Tk，而T={T1,T2,...,Tk}是所有事务的集合。事务中所包含的各个项目记为Ik，所有项目的集合I={I1,I2,...,Ik}。FP-Growth算法首先扫描一遍事务集T，计算事务集T中各项目Ik出现的次数n，并设定最小支持度s（项目出现的最少次数），若项目集I中某个项目Ik的出现次数n小于最小支持度s，则删除该项目，然后将原始事务集T中的各项事务Tk按项目集Ik中的项目频次进行降序排列。之后第二次扫描事务集T，创建项头表以及FP树。项头表的第一列是按照降序排列的频繁项，第二列是指向该频繁项在FP树中节点位置的指针[6]。FP树其实是一棵用来存储项目出现次数的前缀树，每个项目均以路径的方式存储在树结构中，与其它树形结构不同，各项目在FP树中并非只出现一次。只有当项目和频次均不一致时，树结构才会分枝。项目每出现一次，若在FP树中有同路径的节点，则记数增加一次，若无同路径的节点，则相应的新增该项目节点。最终各项目按支持度降序排列，支持度越高的频繁项离根节点越近[7]，从而使得更多的频繁项可以共享前缀。

FP树构建完成之后，依照树结构中从下往上的顺序，对于每个项目找到其条件模式基（CPB，conditional patten base），递归调用树结构，删除小于最小支持度的项。如果最终呈现单一路径的树结构，则直接列举所有组合；非单一路径的则继续调用树结构，直到形成单一路径，即可挖掘出项目的频繁项集。

2 FP-Growth算法在分析学生公共课成绩与专业课成绩相关性中的应用

2.1 学生成绩预处理及离散化

根据FP-Growth算法原理及其实现步骤，本文以某高校计算机专业2018级学生的成绩为数据来源，研究学生公共课成绩和专业课成绩之间的相关性。根据该专业教学计划的具体内容及培养重点，选择高等数学A(一)、大学英语(一)、计算机导论三门课程成绩作为公共课成绩代表，另外选择高级语言程序设计(C++)(一)、数据库原理及应用、数据结构三门课程成绩作为专业课成绩代表，在不考虑学生补考或重修等异常考试的情况下，共得到有效学生成绩数据418条，作为全部的数据来源。限于本文篇幅，随机选取其中的15名学生数据作为研究实例，其公共课和专业课原始成绩如表1所示。为保护学生个人信息，以学号后六位代表对应学生。

表1 学生公共课和专业课原始成绩

学生的成绩数据部分为百分制，部分为五级计分制，为方便FP-Growth算法处理，将学生成绩数据做进一步的离散化处理。若某门课程成绩为五级计分制的优秀或良好，或者其成绩为百分制且分数大于等于80，则认为其成绩优良，将其标注为Ik，反之则不标注。依此规则，将高等数学A(一)、大学英语(一)、计算机导论三门公共课成绩为优良分别记作I1、I2、I3，高级语言程序设计(C++)(一)、数据库原理及应用、数据结构三门专业课成绩为优良分别记作I4、I5、I6。本文主要讨论公共课成绩优良与专业课成绩优良之间的关系，故非优良的成绩忽略不计。原始成绩离散规则如表2所示。离散化后的学生公共课成绩和专业课成绩如表3所示。

表2 原始成绩离散规则

表3 离散化后的学生公共课成绩和专业课成绩

2.2 学生公共课成绩与专业课成绩相关性分析

根据FP-Growth算法思想，通过以下步骤来完成学生公共课成绩与专业课成绩相关性分析。

1)将表3中离散化后的学生公共课成绩和专业课成绩作为事务集T，各项事务中所包含的项目的集合I={I1，I2，I3，I4，I5，I6}。首先完整地扫描一遍事务集T，计算所有学生成绩数据中各成绩项目Ik出现的次数n，得到的结果如表4所示。

表4 各成绩项目Ik出现的次数

2)设定最小支持度s=5。项目集I中成绩项目I2的出现次数n为4，小于最小支持度s，故删除此项目。按出现频次将项目集I重新排序为{I1，I6，I5，I4，I3}，依照此项目顺序将成绩事务集T中的各项事务Tk进行降序排列。删除不符合最小支持度项目并进行降序排列前后的事务集T如表5所示。

表5 删除不符合最小支持度项目并进行降序排列前后的事务集

3)扫描表5中经过删除不符合最小支持度项目并进行降序排列之后的事务集T，创建项头表以及FP树。FP树的根节点记为null，不表示任何项。先根据第一条事务T1={I1,I6,I5}创建FP树的第一条分支，之后将事务T2到T13中的项目逐条插入FP树中。若新加入的项目路径若与现有FP树节点相同，则原有节点数量增加一次；若新加入的项目路径与FP树节点不同，则FP树分枝，增加新的项目节点。以此构建的项头表和FP树如图1所示。

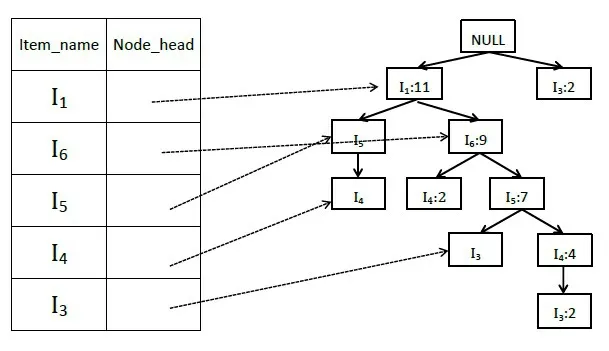
图1 项头表和FP树

4)FP树构建完成之后，查找每个项目对应的条件模式基。以项目I5和I6为例，I5的条件模式基为{I1}、{I1:7，I6:7}，I6的条件模式基为{I1:9}。将I5和I6的条件模式基作为新的事务数据库，以条件模式基的项目为节点，构建I5和I6的条件FP树如图2所示。

由图2可知，I5和I6的条件FP树均为单路径，且每一节点均满足最小支持度，所以直接列举条件FP树中的所有节点组合，与对应项目取并集，即可得对应项目的频繁项集。I5的条件FP树节点组合为{I1:8}、{I6:7}、{I1:8，I6:7}，与I5取并集得到满足最小支持度的频繁项集为{（I1:8，I5:8），（I6:7，I5:7），（I1:7，I6:7，I5:7）}；同理，I6的条件FP树节点组合为{I1:9}，与I6取并集得到满足最小支持度的频繁项集为{（I1:9，I6:9）}。

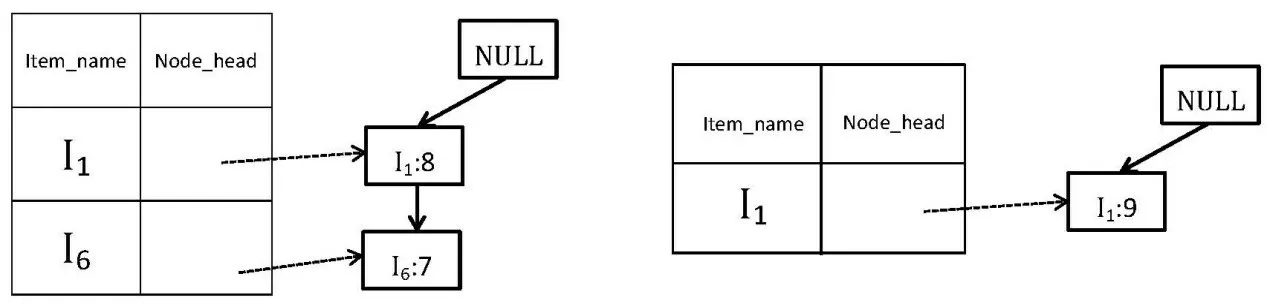
图2 I5和I6的条件FP树

据此分析，I1和I5以及I1和I6之间存在较强的关联性。由此可以得出，如果学生的公共课高等数学A(一)的成绩为优良，则其数据库原理及应用、数据结构两门专业课成绩为优良的概率较大。而大学英语(一)和计算机导论两门公共课成绩未发现与数据库原理及应用、数据结构两门专业课成绩存在明显的关联性。

3 结语

本文指出了高校学生公共课成绩与专业课成绩之间关联的不确定性，通过分析数据挖掘的FP-Growth算法，以某高校计算机专业学生为例，选择高等数学A(一)、大学英语(一)、计算机导论三门公共课成绩和高级语言程序设计(C++)(一)、数据库原理及应用、数据结构三门专业课成绩为数据挖掘对象，将六门课程成绩概化之后引入FP-Growth算法进行分析处理，通过构建FP树等步骤，高效挖掘学生公共课成绩与专业课成绩之间的潜在关系，得出了两者之间的关联规则。这些关联规则可以为高校教学单位课程设置提供有力的理论依据，进而制定更加科学合理的培养计划，促进高校教学模式及人才培养过程的改革。学生也能以此为参考，结合自身成绩特点，灵活调整学习重点，更有针对性地吸收知识，有效提高学习效率。