螺栓拧紧扭矩对其扭矩系数的影响

杨晓辉，伍 川，庞景轩，张 博，江文强

（1.国网河南省电力公司电力科学研究院，河南郑州450052；2.华北电力大学（保定）机械工程系，河北保定071003）

输电线路作为电网最重要的组成部分，对电网的安全运行起着至关重要的作用。在输电线路中，输电铁塔是其中最基础的部分。为了方便施工和安装，输电铁塔的节点构造多采用螺纹连接［1］，螺纹连接由于其具有结构简单、装拆方便、工作可靠等诸多优点，使得螺栓连接成为最普遍的连接方式之一［2］。绝大多数螺栓连接在安装时都必须先拧紧，使其在承受工作载荷之前，预先受到力的作用，防止螺栓松动，增强连接的紧密性。

目前工程中常用的控制螺栓预紧力的方法可以分为扭矩法、扭矩-转角法、预伸长法3种。其中，扭矩法以其操作简单、方便直观的特性，应用最为广泛［3］。针对预紧力矩的确定，目前国内所使用的方法繁多，归纳主要有以下几种：①直接根据标准中给定的扭矩系数K，加以计算或试验获得相关预紧力矩；②根据螺栓的摩擦系数μ，直接选用标准中规定的预紧力矩；③根据螺栓规格直接选用相应的预紧力矩；④根据螺栓制造商试验获得所需施加预紧扭矩［4］。由于扭矩法中拧紧系数常根据加载经验以及加载条件进行选取，其不确定性会影响预紧力的加载结果，因此，有必要对扭矩系数的变化规律进行研究。

而通过控制扭矩来施加螺栓预紧力时，扭矩系数是一个十分重要的参数。王朋等［5］对输电塔中常用的M16镀锌螺栓进行了预紧力试验研究，测试分析了螺栓强度等级、有无垫圈和有无润滑对螺栓连接副扭矩系数的影响。Croccolo等［6］设计出一种得到螺栓摩擦系数的试验方法，并由摩擦系数和夹持件拉伸状态得到扭矩系数。郭历伦等［7］开展多螺栓连接结构预紧力实验研究，获得了其在纯拧紧力矩作用下的预紧力及其响应规律。张和平等［8］通过多功能螺栓紧固分析系统对紧固件进行转矩预紧力实验，得出摩擦系数随拧紧速度增大而减小。这些研究均是从各方面探究了影响扭矩系数的因素，给出了摩擦系数对扭矩系数的影响规律，为扭矩系数的研究提供了重要的参考［9-13］。

本文通过对螺栓连接理论进行分析，推导给出了扭矩系数的理论表达式。以输电铁塔中常用的M16螺栓进行扭矩法的预紧力加载实验，并对螺栓施加预紧力过程进行仿真分析，研究扭矩系数随拧紧扭矩的变化规律。

1 扭矩系数理论

在图1（a）所示的矩形螺纹中，当在轴向力Fb作用下的螺母受到一切向力Uf的作用，使其向Fb的反方向转动时。再根据同图1（b）所示的螺纹面上螺母单元各力平衡的关系，可得［14-15］

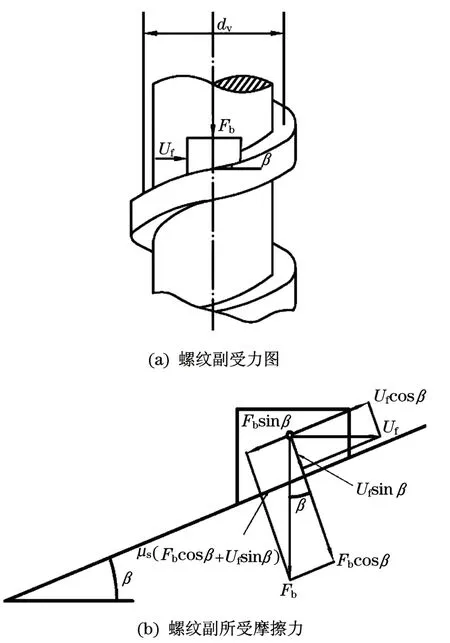
图1 矩形螺纹的轴向力F b与切向U f的关系Fig.1 Relationship between axial force and tangential force of rectangular thread

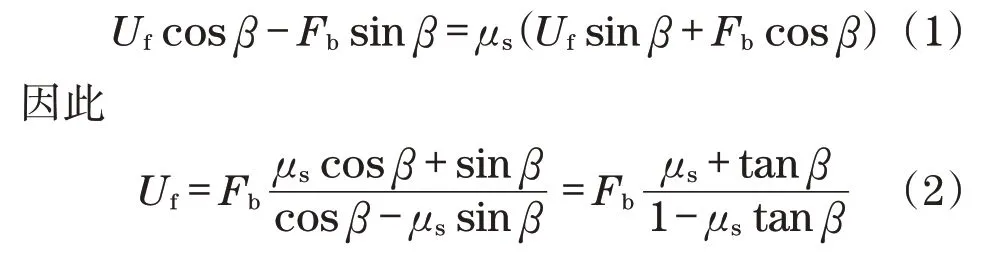
式中：μs为螺纹面的摩擦系数；β为螺纹升角。

如果螺纹面的摩擦角是ρ，则由μs=tanρ，式（2）变化为

如螺纹的有效直径为dp，则紧固螺纹副时的扭矩Tf为

在螺纹联接体中，施加在螺母上的拧紧扭矩Tf等于式（4）右边的力矩与克服螺母支承面摩擦的力矩之和，其表达式为

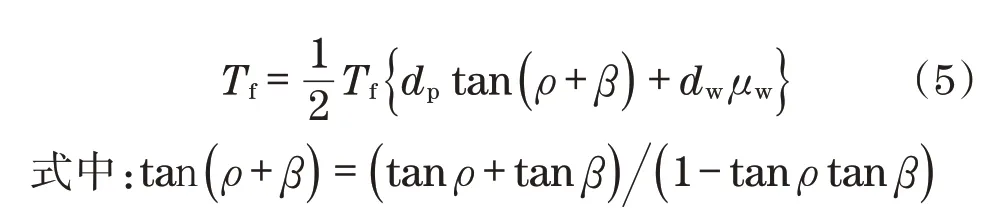
由于β一般为2~30，因此tanβ趋近于0，故略去微小量tanβ，并取

式中：Ff为螺栓中产生的预紧力；dp为外螺纹的有效直径（计算时采用标准尺寸d2）；β为螺纹升角，此处P为单头螺纹的螺距；μs为螺纹副的摩擦系数；μw为支承面摩擦系数；dw为螺母支承面摩擦力矩的等效直径。

当压力均匀分布时，支承面为以螺母对边距离B为直径的圆面积，如螺栓孔直径为D，则此直径可用下式计算：

由式（9）我们可以看出，对于同一类型螺栓螺纹升角β、螺纹副摩擦系数μs、支撑面摩擦系数μw都为常数，故式（8）可以简化为

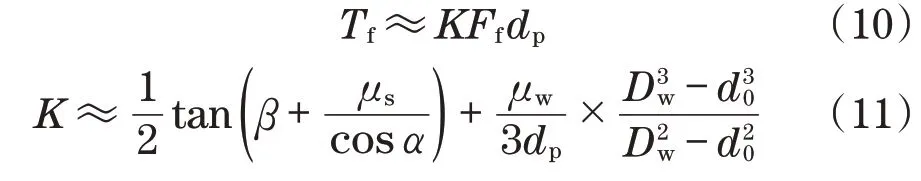
式中：K为工程中常用的扭矩系数。

由式（9）我们可以知道螺纹副摩擦系数与支撑面摩擦系数对K的影响很大。

2 拧紧扭矩实验

通过螺栓拧紧扭矩实验，可以得到螺栓预紧时施加扭矩和螺栓预紧力的关系，进而通过式（10）求得扭矩系数。本研究进行螺栓拧紧扭矩实验时采用的实验装置如图2所示。实验装置整体为一“上”字型固定装置，包括底座、支架以及横板，3部分焊接在一起形成一个整体。实验螺栓在对称的位置上各贴有一片应变片，从而实现对螺栓预紧力的测量。该实验装置底座可通过螺栓进行固定，横板上有一螺栓孔，螺栓孔两侧开有扩槽，实验时螺栓两侧应变片沉入扩槽中，避免应变片被挤压破坏而影响实验结果。横板底面有一方形沉槽以及向两侧延伸的引线槽，实验时将螺栓头沉入方形沉槽中，防止螺栓产生转动，应变片引线黏附于引线槽中，使得测量结果更准确，避免扰动。实验时通过动态应变仪实现螺栓预紧力的精确测量，螺栓扭矩使用数显扭矩扳手进行施加。

图2 实验装置示意图Fig.2 Experimental device schematic

要通过螺栓杆上应变片的数据得到预紧力，就需要知道螺栓的刚度。搭建如图2所示的实验装置，试验前，首先将被试螺栓的螺杆部分打一个10 mm的小孔，这个小孔是为了穿入一个M9的螺栓，将钢丝拧紧在被试螺栓表面，以保证试验加载过程中钢丝不会滑落。将螺栓穿过支架上的预留孔，再将铁丝穿过螺栓，铁丝下端与砝码箱相连。在螺栓光杆对称贴一组应变片，用于测量螺栓杆的轴向应变。

由理论分析过程可知，螺栓头与被连接件以及螺母支撑面间的摩擦系数会影响螺栓扭矩系数，而在螺栓与螺母材料相同的情况下，这两个位置的摩擦系数常认为是相同的。因此，在进行螺栓松动实验前要先对螺栓头与被连接件和螺母支撑面间的摩擦系数进行确定。

测量砝码箱空重后，用两个螺栓将支架固定在振动平台上。将被测试螺栓（打孔）置于支架开口，先使用铁丝穿过被试螺栓上的孔把砝码箱的挂线缠紧在螺栓上，再使用夹子把砝码箱的挂线夹紧，限制其摆动，在螺栓杆下加载质量已知的砝码，同时记录下对应载荷下应变片的数据。通过如下公式求得螺栓刚度：

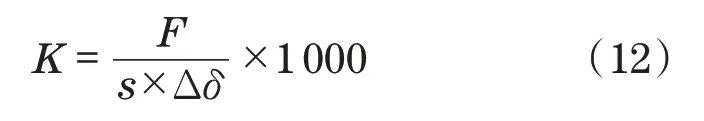
式中：K为螺栓刚度；F为螺栓轴向载荷（即预紧力）；s为螺栓横截面积；Δδ为螺栓杆轴向应变。

同时根据公式

式中：Tb为螺母与连接板之间摩擦力；Fb为接触面摩擦力矩；db为螺母与连接板之间摩擦力的等效力矩；μw为连接板面摩擦系数。

使用图3所示实验装置，在螺栓杆下加载质量已知的砝码，砝码重力即为螺栓所受预紧力。同时使用数显扭力扳手扭动螺栓，记录下最大扭矩，这个扭矩即为克服螺栓头的摩擦力的扭矩，即可得到螺栓头摩擦系数。

图3 螺栓刚度测定实验装置Fig.3 Bolt stiffness measuring experimental device

3 实例分析

该组M16螺栓测得螺纹副的摩擦系数μs=0.154 5，支承面摩擦系数μw=0.293 2。将表1参数带入式（11），求得扭矩系数K，同时，计算得到不同拧紧扭矩下对应的预紧力。给出实验与仿真中每组拧紧扭矩下所对应的扭矩系数K，将数据整理在表2中。

表1 M16螺栓参数Tab.1 For mula parameter

表2 不同拧紧扭矩下扭矩系数Tab.2 Torque coefficient under different tightening tor que

同时使用有限元仿真验证算例的正确性，使用Solid Work软件来进行三维实体模型的建立，如图4所示。根据GB/T 5782—2016和GB/T 6170—2015，建立M16六角螺栓三维模型并进行模拟装配。建立三维实体模型后导入ANSYS Workbench，建立有限元模型。螺纹接触面、连接件与螺栓头、螺母接触面的接触性质都设定为Frictional。同时在连接板上下平面和螺母下表面都施加固定约束。此次仿真目的为模拟螺栓预紧过程中，施加预紧扭矩与螺栓预紧力之间的关系。改变施加的预紧扭矩大小，得到在不同扭矩下的螺栓预紧力。在螺栓头上施加一个绕轴心的顺时针的扭矩，模拟预紧时螺栓向连接板的旋入。

图4 螺栓连接有限元模型Fig.4 Finite element model of bolted connection

如表2所示，在实际情况中，在小拧紧扭矩（小于40 N·m）的情况下，扭矩系数基本不变。在较大扭矩情况下，扭矩系数随着扭矩的增大而增大，扭矩每增加10 N·m，扭矩系数增大1.06倍。这是由于随着拧紧扭矩的增大，支撑面表面状态发生改变，摩擦系数增大，拧紧扭矩需要克服更多摩擦力的原因。

从图5中我们不难看出实验结果与仿真结果，扭矩系数K的变化规律一致，证明实验方案是合理的。

图5 不同拧紧扭矩下扭矩系数Fig.5 Torque coefficient under different tightening torque

4 结论

本文通过螺纹副受力分析，推导出扭矩系数的表达公式，并通过对螺栓施加拧紧扭矩的实验和仿真，探究扭矩系数K随着拧紧扭矩的变化而变化规律，得出以下结论：①通过螺纹副受力推导出来的扭矩系数公式在拧紧扭矩较小的时候（小于40 N·m）与实际情况较吻合。②在拧紧扭矩较大的情况下，扭矩系数会随着拧紧扭矩的增大而增大，平均拧紧扭矩每增大10 N·m，扭矩系数提高1.06倍。③实验与仿真中扭矩系数要比理论值大，这是因为经典理论没有考虑螺栓变形及表面状态变化的原因。