高速电梯轿厢整流罩气动噪声研究

陈继文，王 磊，甄 涛，苏 强，李 鑫

（1.山东建筑大学机电工程学院，山东济南250101；2.济南市特种设备检验研究院，山东济南250102）

随着电梯朝着高速方向不断地发展，噪声成为影响电梯乘客舒适度的重要指标。机械噪声和气动噪声是高速曳引电梯噪声的主要噪声源，而在轿厢顶部和底部增加整流罩是控制高速电梯风噪声的重要措施［1］。整流罩的设计涉及空气动力学、结构动力学、噪声学甚至美学等一系列学科［2］。整流罩外形设计对降低高速电梯的振动噪声起着重要作用。从设计目标上看，整流罩外形及相关尺寸的设计要尽可能减振降噪，同时还考虑到整流罩在有效寿命内能抵抗疲劳载荷和维修方便等。为了满足这些要求，需要考虑整流罩的结构、材料、成本和加工工艺性等方面问题［3］。文献［4］研究了脊状结构的整流罩，并得出了当锥角θ=150°时，其受力效果最好的结论，但未分析其他形状的整流罩；文献［5］提出载质量为1 000 kg、拱顶高为1.0 m的椭圆形整流罩方案在减小电梯轿厢阻力、消除轿厢尾部涡流、减小气动噪声及工程实用性方面有较好的效果。本文运用计算流体力学（Computational Fluid Dynamics，CFD）仿真技术分析轿厢外形与气动噪声的关系，研究了高速电梯轿厢及其上下两端分别安装锥形整流罩和拱形整流罩时，轿厢周围流场与气动噪声特性以及整流罩对轿厢气动噪声的影响，并对轿厢高速运行产生的流场进行了仿真验证，为高速电梯整流罩的设计提供了有益参考。

1 高速运行电梯轿厢的切应力分析

轿厢对电梯的额定速度有重要影响，需要优化轿厢结构以减小其高速运行时产生的切应力，降低由此造成的轿厢振动与噪声。轿厢及整流罩三维模型图如图1所示。

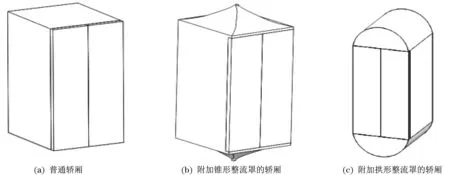
图1 轿厢及整流罩三维模型图Fig.1 Three-dimensional model diagram of elevator car and fairing

研究轿厢在井道内运行时所受的气动力，首先要确认轿厢在井道内收受到的经常以黏性阻尼作［6-7］。图2为普通轿厢受黏性阻尼的现象，则气流对轿厢的切应力表达式为

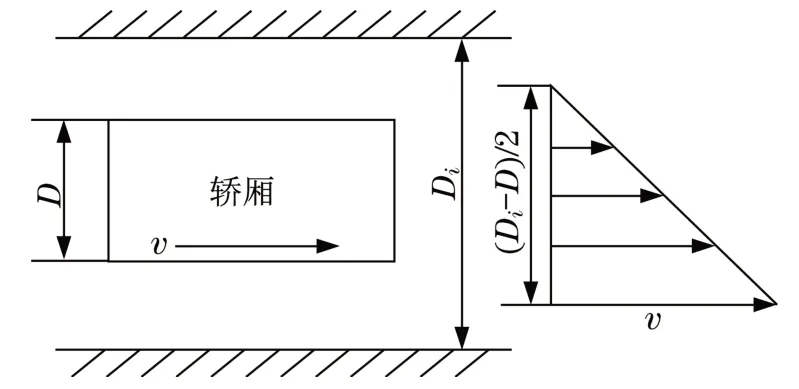
图2 普通轿厢受黏性阻尼现象图Fig.2 Viscous damping phenomenon of ordinar y elevator car

为了研究方便（见图2），把速度近似看作线性分布，即轿厢内壁流体流速为零，而轿厢外壁流体流速为v，则速度梯度为

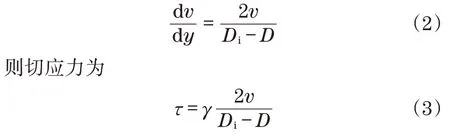
式中：γ为流体（空气）的黏度，MPa·s；v为流体（空气）的速度，m/s；D为轿厢的宽度，m；Di为井道的宽度，m。

井道中轿厢侧面上的切应力对轿厢产生的阻力FR为

式中：AP为轿厢的侧面积。

轿厢向上运动所引起的气流运动主要包括：因活塞效应导致一部分风向井道上方流动形成活塞风，另一部分风则会在轿厢底面推动下向上方运动［8］。电梯井道壁与轿厢壁均设置为绝热墙体，电梯井道两端的通风口均设置为随压力变化的自由通风口，井道内的空气按可压缩理想流体考虑，轿厢动力学模型图，如图3所示。轿厢额定运行速度为VC，入口的风速为Vin，出口的风速为Vo，活塞风速为W，向上运动的风速为U，a-a、b-b、c-c、d-d为截面位置标记。由切应力计算可知，空气流速越小，切应力值越小。由于形成的切应力是不规则分布的，造成轿厢发生水平晃动，机械碰撞会产生噪声。

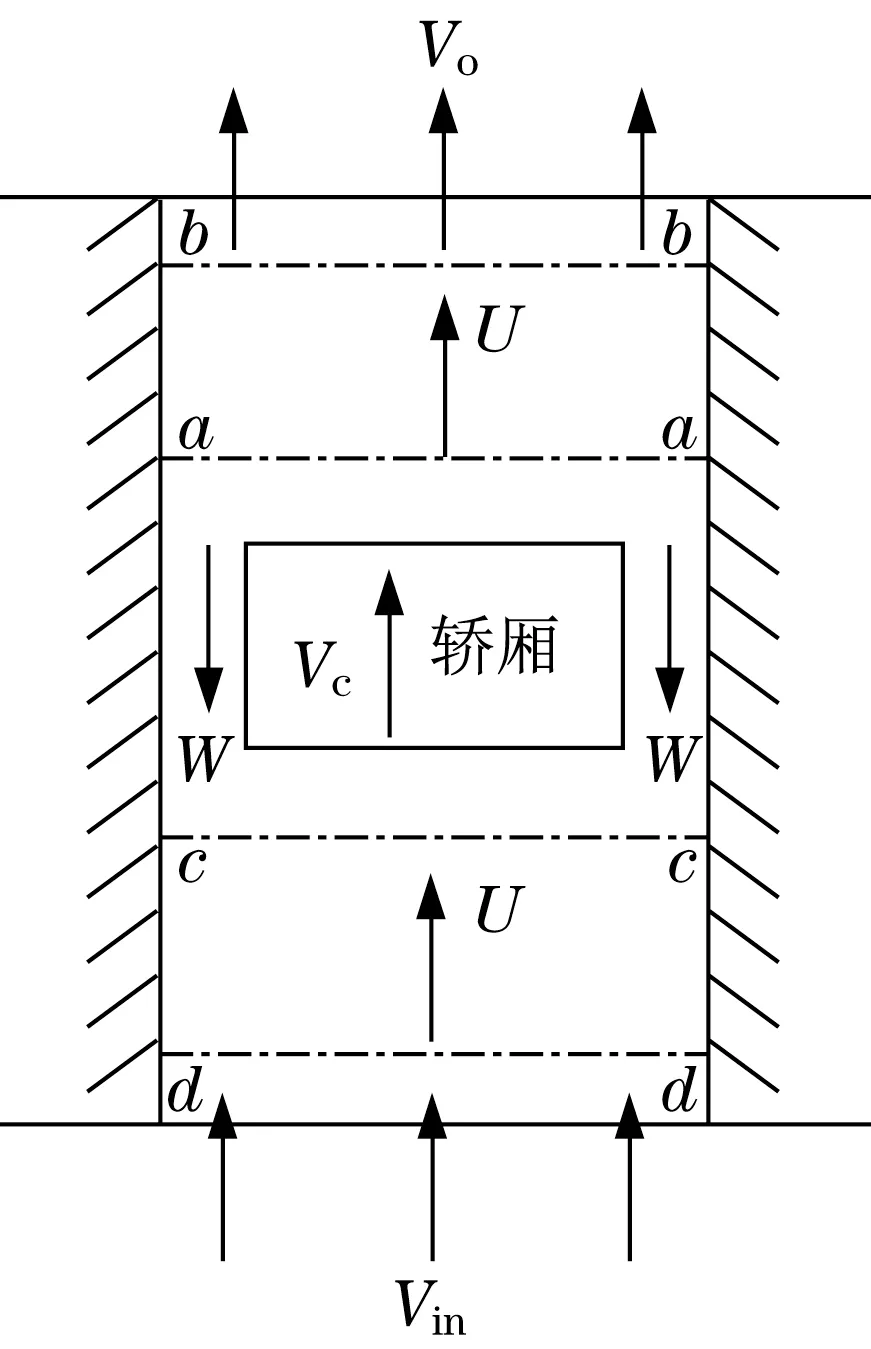
图3 轿厢动力学模型图Fig.3 Dynamic model diagram of elevator car

2 轿厢整流罩CFD仿真分析

2.1 SST k-ω两方程模型

剪切压力传输k-ω模型SSTk-ω湍流模型是一个两方程涡黏性湍流模型，既可应用于低雷诺系数的湍流模型，没有额外复杂的黏性衰减函数，又可应用在远离壁面的地方即边界层以外的区域。相比标准k-ω模型，SSTk-ω模型合并了源于ω方程中的交叉扩散，在建立湍流黏度模型时，考虑到了湍流剪应力的传输。另外，采用了不同的模型常量。这些改进使得SSTk-ω模型比标准k-ω模型在广泛的流动领域中有更高的精度和可信度。SSTk-ω流动方程如下［9-10］：

湍动能运输方程为

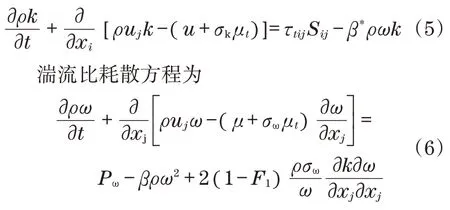
式中：ρ为流体密度；u为速度；t为时间；x为坐标轴（i，j=1，2，3，分别表示x、y、z三个空间坐标）；k为湍流动能；ω为比耗散率。

在式（5）和式（6）中，雷诺应力的涡黏性模型为

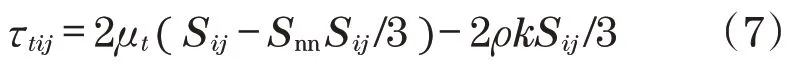
式中：μt=ρk/ω为涡黏性；Sij为平均速度应变率张量；Snn为克罗内克算子；Pω为生成项，

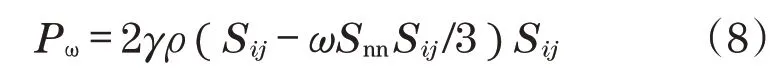
式中：F1、β、γ、σw、σk、σm均为模型参数；β*为模型常数，取0.09。

2.2 CFD仿真模型的建立

设定针对运行速度为8 m/s，额定载质量1 000 kg的单井道高速电梯进行研究计算。电梯井道截面为2 200 mm×2 100 mm的矩形，电梯轿厢截面为1 600 mm×1 400 mm的矩形，轿厢的高度为2 500 mm。分析流经轿厢壁的气流速度和压力分布需要将电梯井道内表面、轿厢和整流罩外表面封闭成一个完整的计算域。本次计算速度和压力分布只取局部区域，以尽可能避免空气流动方向对计算结果的影响。仿真分析，对几何模型作如下简化：风道系统密封性良好，除进风口和出风口没有空气泄露；空气为不可压缩流体，且密度为常数［11］。由于需要得到轿厢运行时流经轿厢壁外侧的气流速度和沿轿厢壁外侧的压力分布，所以采用前处理软件ICEM对封闭后的整个计算域进行网格划分，将刚体作柔性化处理。先进行拓扑构建，检查几何错误，同时生成特征线，创立外部域（计算域），这是流体运行的空间，Z取2 200/1 600=1.375，X取2 100/1 400=1.5，Y取2；然后进行网络参数设置，对刚体柔性化进行网格划分，最后导入到Fluent求解器中进行仿真计算。对于轿厢及其分别附加锥形整流罩、拱形整流罩，采用相同的网格划分加密方式，3种不同轿厢的网格示意图，如图4所示。

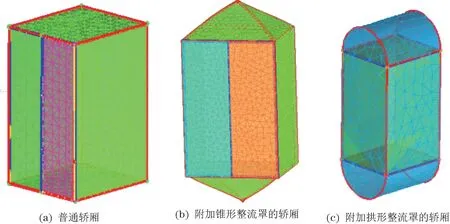
图4 轿厢及整流罩体网格示意图Fig.4 Grid diagram of elevator car and fairing body

2.3 边界条件

在计算中，边界条件的设置如表1所示。

表1 边界条件Tab.1 Boundary conditions

2.4 仿真结果对比分析

由图5所示的3种不同轿厢的气流沿轿厢壁速度分布云图可见，普通轿厢顶部上面形成的活塞风速为8 m/s，锥形整流罩轿厢顶部上面形成的活塞风速为7.5 m/s，拱形整流罩轿厢顶部上面形成的活塞风速为7 m/s。根据风噪与流体流速的五次方或六次方成正比，可知附加锥形整流罩的轿厢形成的涡流比普通轿厢小一些，且普通轿厢上方和底部形成较大涡流，对轿厢顶部造成较大的振动与噪声，附加锥形整流罩后对轿厢起到了缓冲气流和减小涡流的作用。相比于锥形整流罩，拱形整流罩在缓冲气流、降低噪声等方面表现出更好的性能。由图5所示，安装拱形整流罩后，轿厢顶端和底端产生的涡流都大大减小。

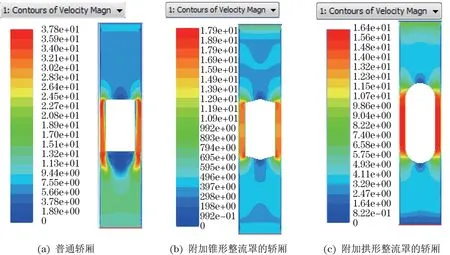
图5 3种不同轿厢的气流沿轿厢壁速度分布云图Fig.5 Cloud diagram of airflow distribution along car wall velocity in three different elevator cars compartments

气流在经过电梯时不断被加速，其静压不断的下降，在电梯的尾部，由于存在很强的漩涡，压力也很低。这种强大的压力梯度使得高速运行的电梯表面从前缘到尾缘有很大的压力差，而且高速气流还对电梯表面作用有很大的黏性曳力。因此，在电梯井道中高速运行的电梯会受到很强的气动阻力，造成很大的能源浪费。图6为3种不同轿厢的静压沿轿厢壁分布云图，可见加装锥形整流罩的轿厢外壁所受的压力比普通轿厢均匀一些。压力分布越不均匀轿厢壁受到的冲击越大，受力不均程度也就越大，尤其在普通轿厢上方直接生成巨大压力块，压力分布对轿厢稳定性影响极大，而加装锥形整流罩后确实起到了缓冲气流、均匀压力的效果，由图6（b）、图6（c）可知，相比于锥形整流罩，拱形整流罩使轿厢顶端和底端的压力分布更加均匀，产生的振动与噪声也更小。轿厢底部安装的整流罩可以减弱由于气流的流动分离产生的低压区，有效地降低气动阻力的大小。在轿厢顶部安装的整流罩能够进一步降低气动阻力，有效地减弱轿厢上壁面对空气的滞止作用，减小轿厢顶部压力。

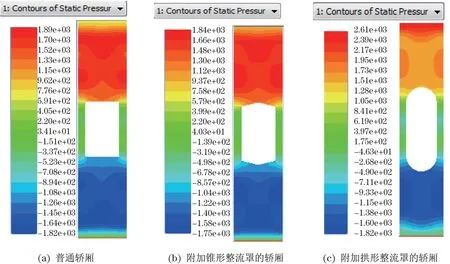
图6 3种不同轿厢的轿厢壁压力分布图Fig.6 Pressure distribution diagram of car walls of three different elevator cars

通过Fluent仿真进一步分析不同拱顶高度对拱形整流罩的影响，当拱顶高度分别为0.2、0.3、0.4、0.5、0.6和0.7 m 6个高度值时，轿厢的流体流速分布图、静压分布图与动压分布图分别如图7~图12所示。可见轿厢顶部的气流流速较低，但静压力值却很大，可达到180 Pa以上，呈蘑菇状分布，其原因是轿厢上升速度较快，顶部受到较大阻力，造成顶部压力增大。当拱顶高度分别为0.2、0.3、0.6和0.7 m时，轿厢顶部压力都超过300 Pa，甚至是拱顶高度分别为0.4、0.5 m时的两倍；当拱顶高度为0.4 m时，静压分布最为均匀，形成的涡流最小。仿真时，电梯轿厢相对于远处的空气相对速度取值为8 m/s，忽略了竖井两端通气口的影响；而实际运行时，电梯井道内的空气会有一部分从通气口流出或流入，因此，电梯轿厢相对于远处气体的速度应略小于8 m/s。流体流速越小，在轿厢上形成的静压也会越小，在轿厢实际运行时，由于流体实际速度不到8 m/s，整流罩之间的压差会更小。从流场流速上看来，当拱顶高度为0.2 m时大部分区域流速约为8.4 m/s；当拱顶高度分别为0.3、0.4 m时大部分区域流速约为9.5 m/s；当拱顶高度分别为0.5、0.6 m时大部分区域流速约为10 m/s；当拱顶高度为0.7 m时大部分区域流速约为12 m/s。电梯轿厢表面静压随曳引速度的增加成平方倍增加［12］，故拱顶高度为0.7 m时气动噪声最大。

图7 整流罩拱顶高度为0.2、0.3和0.4 m时流体流速分布图Fig.7 When the fairing vault height is 0.2，0.3 and 0.4 m air velocity distribution

图12 整流罩拱顶高度为0.5、0.6和0.7 m时动压分布图Fig.12 When the fairing vault height is 0.5，0.6 and 0.7 m Dynamic pressure distribution

从形成的涡流来看，当拱顶高度分别为0.2、0.3和0.7 m时产生的涡流很大，对轿厢的冲击很大，涡流会对轿厢运动产生较大波动，会引起轿厢的晃动，使运行不平稳，加剧运行过程中产生的振动，引发噪声。此外从流体流速图中发现，拱顶高度分别为0.2、0.3、0.4、0.5和0.6 m时涡流发生的位置在轿厢底部位置，拱顶高度为0.7 m时涡流发生的部位是在轿厢顶部位置，且涡流较多，中部区域也有涡流产生；拱顶高度分别为0.2、0.3 m时在轿厢底部位置发生的涡流较大，对振动的影响也就很大。综上可知，拱顶高度分别为0.4、0.5和0.6 m时产生的涡流较小。

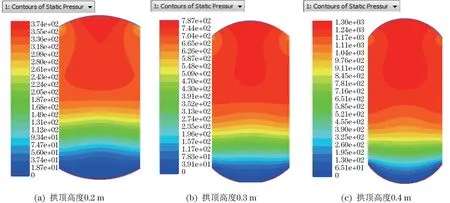
图9 整流罩拱顶高度为0.2、0.3和0.4 m时静压分布图Fig.9 When the fairing vault height is 0.2，0.3 and 0.4 m static pressure distribution

图10 整流罩拱顶高度为0.5、0.6和0.7 m时静压分布图Fig.10 When the fairing vault height is 0.5，0.6 and 0.7 m static pressure distribution

从图11和图12所示轿厢的动压分布图可见，随着拱顶高度的增大，动压逐渐增大，从40~90 Pa变化不等。当拱顶高度分别为0.2、0.6 m时轿厢底部产生的动压涡流较大；当拱顶高度为0.7 m时轿厢顶部产生的动压涡流较大，而且轿厢中部也存在很大涡流，动压图分层较多，对轿厢稳定性不利；当拱顶高度分别为0.4、0.5 m时轿厢底部产生的动压涡流较小，尤其拱顶高度为0.4 m时涡流最小。从流体流速分布图和动压压力分布图上都可以发现，电梯轿厢底部区域内存在两个涡流区，其主要原因是气流以较高的速度从轿厢与井道壁之间的缝隙快速流出，并以较高的速度向下运动，而电梯轿厢底部附近区域流体的流速很小，由此形成了非定常旋涡。此时电梯轿厢周围的空气雷诺数都比较大，使得靠近轿厢的高压不足以把附面层推到轿厢的背面。这种非定常漩涡的不断脱落和演化会使流场中的压力分布产生剧烈的波动，并导致轿厢表面受到的顺流向阻力和横向升力呈现周期或非周期的变化，出现紊乱状态。对于非周期变化的流体动力，由于电梯的结构阻尼和气动阻尼的共同作用，周变化的流体动力会被慢慢地消耗掉；但是周期性变化的流体动力却具有负阻尼的性质［13］，具体表现在轿厢结构与井道中的流体相互作用，并从中吸收能量而不是消耗能量，使原本轻微颤抖的轿厢结构的振动幅度会被进一步放大，特别是当涡流脱落的频率与系统振动频率连锁在一起时，会使电梯产生共振。因此，形成的涡流将会出现周期性的波动。从图7和图8可以看出，形成的涡流会周期性的从轿厢尾部脱落，从图6可以看出从轿厢底部形成的涡流会被带到井道底部。这些形成的涡流使轿厢底部形成了一个较大的负压区，增大了轿厢运行所受的阻力，导致轿厢发生周期性的振动，产生较大的噪声。将对轿厢乘坐的舒适性造成负面影响，还可能会缩短轿厢上的主要部件的使用寿命，甚至影响到电梯的安全性。

图8 整流罩拱顶高度为0.5、0.6和0.7 m时流体流速分布图Fig.8 When the fairing vault height is 0.5，0.6 and 0.7 m air velocity distribution

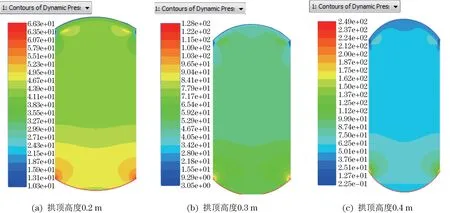
图11 整流罩拱顶高度为0.2、0.3和0.4 m时动压分布图Fig.11 When the fairing vault height is 0.2，0.3 and 0.4 m Dynamic pressure distribution

3 结语

通过对轿厢流体力学理论与仿真分析，发现轿厢存在严重的气动力学缺陷，主要表现为在轿厢的顶部和底部容易形成严重的涡流，引起轿厢的振动，产生较大的噪声，而通过在轿厢底部和顶部加装整流罩可以有效地解决轿厢阻力、消除轿厢尾部涡流、减小气动噪声等方面的问题。通过仿真分析可见，拱形整流罩相比于锥形整流罩能更有效地降低高速电梯运行的气动噪声。通过对附加拱形整流罩轿厢高速运行的仿真分析可见，当拱顶高度为0.4 m时轿厢所受的阻力较小，产生的涡流也较小，高速气流对轿厢的振动与噪声影响较小，所受力学性能比较好，是6个方案中的最佳方案，为高速电梯整流罩的设计提供了有益参考。