基于BN和T-S模糊故障树的起重机变幅机构可靠性评估
李 鹏,徐格宁
(1.山西工程职业学院机械制造工程系,山西太原030009;2.太原科技大学机械工程学院,山西太原030024)
汽车起重机是一种装在汽车底盘上的起重机,因为其移动灵活、操作方便,在需要吊装的场合都可以看到它的身影,所以,它在工程机械中的地位不言而喻。汽车起重机的液压系统是汽车起重机重要的组成部分,在使用过程中液压系统故障是比较常见的,但由于液压系统具有结构关系复杂、关联性强等特点,使得故障诊断难度相对较大。由于汽车起重机的工作特性,液压系统一旦失效造成的损失是相当大的,所以准确、科学、合理地对汽车起重机液压系统进行可靠性评估是非常有必要的。本文采用T-S模糊故障树代替传统故障树之后转换为贝叶斯网络的方法,应用模糊数来描述故障状态,对液压系统进行可靠性分析,由于T-S模糊故障树可以描述事件之间的不确定关系,因此,这种方法更贴合复杂液压系统的实际情况。
1 基于T-S模糊故障树的贝叶斯网络的构建
T-S模糊故障树是在传统的故障树基础上发展而来,其在描述事件间不确定的逻辑关系、故障的多态性以及模糊性方面有着较强的优势,但是,T-S模糊故障树计算分析时计算量巨大,且不能反向推理,因此,在工程应用中受到了一定的局限。贝叶斯网络适用于复杂的系统,能够反向推理,将T-S模糊故障树与贝叶斯网络结合将能利用它们各自的优势,克服各自的不足。构建基于T-S模糊故障树的贝叶斯网络分2步:①将T-S模糊故障树向贝叶斯网络映射;②确定贝叶斯网络的条件概率表参数。
1.1 贝叶斯网络的构建
建立好的T-S模糊故障树与贝叶斯网络是相互对应的,T-S门中的基本事件、中间事件、顶事件和T-S门分别对应贝叶斯网络中的根节点、中间节点、叶节点和有向边。
1.2 条件概率参数表的确定
由于T-S模糊故障树应用模糊数表示事件的多种状态以及故障程度,T-S门规则可以独立的表述条件概率,所以贝叶斯网络条件概率表与T-S门的规则是具有类似性的。贝叶斯网络的条件概率参数表可以通过T-S门规则进行赋值。

通过对T-S模糊故障树向贝叶斯网络转换,多态系统经过转换可以映射为贝叶斯网络,而且经过转换之后能够保证系统模型的完整性和统一性。
2 基于T-S模糊故障树的贝叶斯网络叶节点概率、后验概率和重要度算法
2.1 叶节点各故障状态的发生概率

2.2 系统事件的后验概率
在叶节点T故障状态为Tq的条件下,利用贝叶斯公式的特性可以对系统进行逆向推理,根节点x i故障状态为x aii的后验概率为

当系统出现故障之后,各底事件出现故障的概率,通过后验概率的计算可以对系统可靠性进行合理的分析,有利于进一步了解系统情况。
2.3 根节点重要度计算
重要度是系统可靠性计算的关键环节,根节点的重要度反映了其发生故障对于叶节点的影响程度,重要度的计算对于提升系统的可靠性与安全性具有积极意义。
2.3.1 概率重要度
概率重要度表示根节点在某种故障状态下单独引起叶节点为某种故障状态的发生概率。根节点x i在故障状态为x ai i时叶节点T故障状态为Tq的概率重要度计算公式为


式中:ki为根节点x i故障状态的个数。
2.3.2 关键重要度
相比于概率重要度,关键重要度计算的是根节点与叶节点在故障概率的变化率的比值,关键重要度的计算需要概率重要度的计算作为前提。根节点x i在故障状态为x ai i时叶节点T故障状态为Tq的关键重要度为
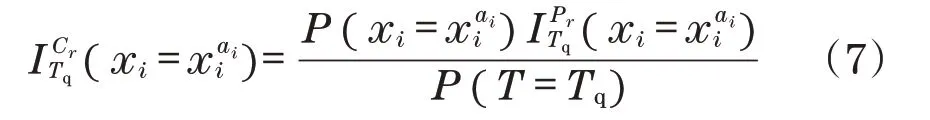
则根节点对于叶节点故障状态为Tq的关键重要度为

3 汽车起重机液压变幅系统实例分析
现对某型号的汽车起动机变幅液压系统进行分析,其液压原理如图1所示。汽车起重机的变幅机构主要作用是改变吊臂与地面之间的夹角,从而实现改变作业半径与作业高度的目的。其原理为当手动联动换向阀处于中间位置时,液压泵油压通过换向阀卸荷,变幅液压缸不工作;当换向阀处于左边位置时,液压泵将油压通过换向阀以及平衡阀进入液压缸底部,同时两液压缸并联,保证两液压缸活塞杆同步伸出,实现吊臂仰角增大;当换向阀处于右边位置时,液压泵压力进入液压缸上部,同时一部分压力将顺序阀打开使得液压缸下部的油能经过顺序阀回到油箱,实现吊臂仰角变小。
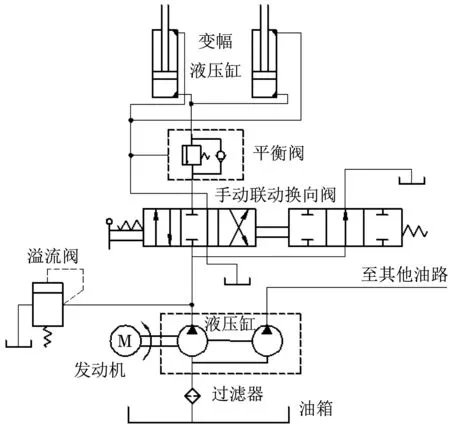
图1 汽车起重机变幅机构液压系统原理图Fig.1 Schematic diagram of hydraulic system for luffing mechanism of truck crane
以汽车起重机变幅机构常见的故障液压缸爬行为顶事件,建立T-S模糊故障树(如图2所示),其中,T(变幅机构液压缸爬行)为顶事件,x1(液压泵密封件损坏)、x2(吸油过滤嘴堵塞)、x3(液压泵磨损)、x4(液压油清洁度低)、x5(油液混有空气)、x6(油量不足)、x7(溢流阀故障)、x8(换向阀故障)、x9(平衡阀故障)、x10(导轨润滑不良)、x11(装配制造精度差)、x12(液压缸内存有气体)、x13(活塞杆弯曲)、x14(活塞杆与其他零件同轴度差)、x15(液压缸密封件失效)和x16(液压缸内磨损)为底事件;y1(油源部分故障)、y2(控制部分故障)、y3(执行部分故障)、y4(液压泵故障)、y5(液压油)、y6(导轨阻力不均)、y7(液压缸故障)、y8(活塞杆故障)、y9(缸内泄露)为中间事件。
对于事件的描述采用0表示无故障,0.5表示轻微故障,1表示出现故障,采用梯形隶属函数,取s1=s2=0.1,m1=m2=0.3[6],结合工程实际与专家经验,列出故障树中各个T-S门规则,由于篇幅所限只列出部分T-S门规则,如表1所示。
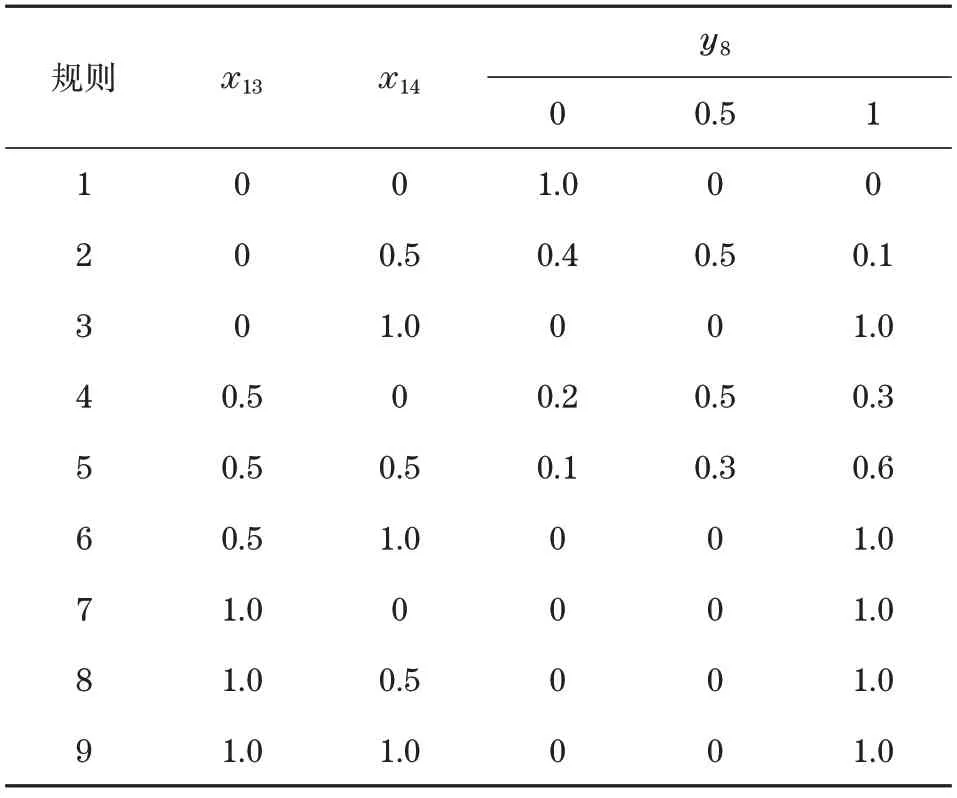
表1 T-S门规则1Tab.1 T-S gate rule 1
根据前面的介绍,将T-S模糊故障树转化为模糊BN的有向无环图,各节点的条件概率依据T-S模糊故障门的规则进行映射。
在实际的工程场景中,故障率数据的获取一般通过专家的经验结合现场数据进行判断,再将所有专家的判断进行加权平均得到故障。这种方法不能够体现出专家对于自己的判断的信心程度,本文采用“信心指数法”[7]对传统的专家调查法得到的数据进行修正,通过选取部分设计人员、一线操作人员、维护人员等有经验的专家,结合他们的工龄、职称、学历等因素,分配不同的权重:

专家构成表如表2所示。
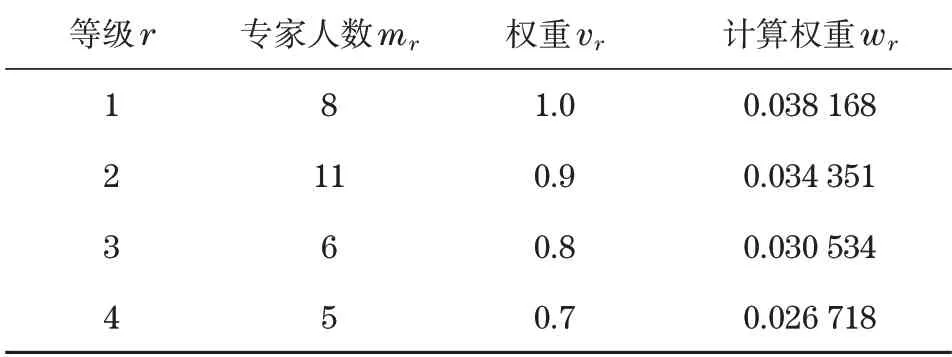
表2 专家权重分配Tab.2 Expert weight allocation
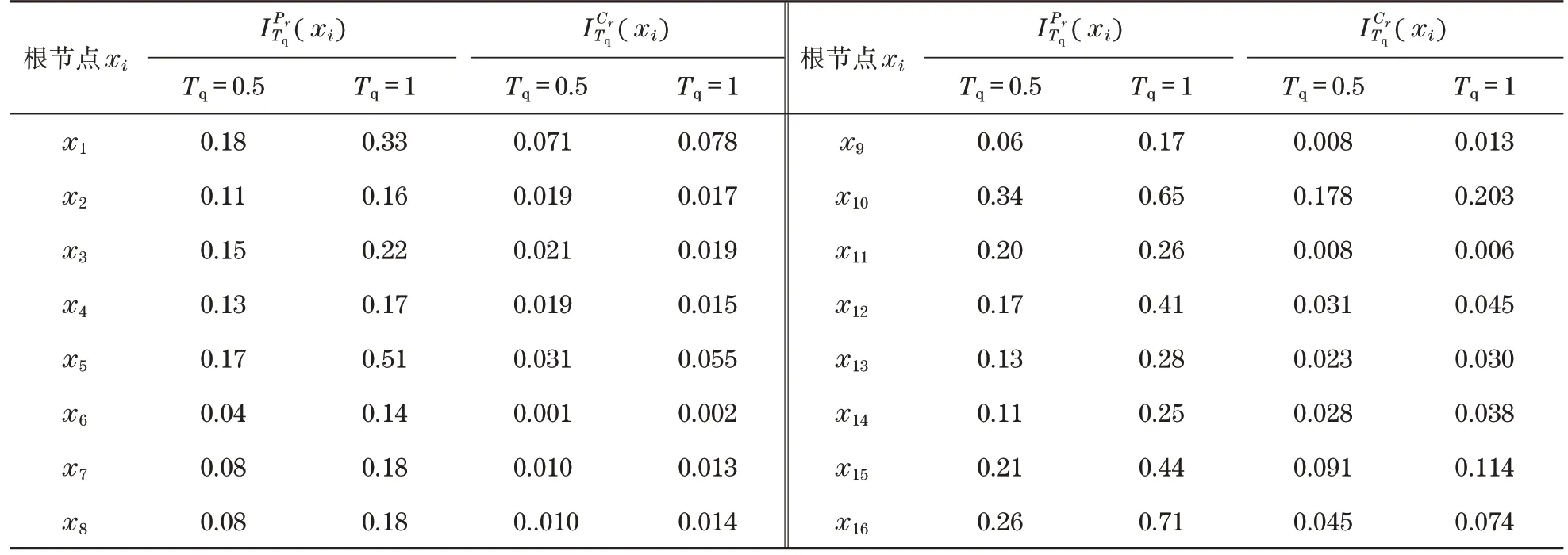
(1)假设参与调查的专家人数为m,根据表3的规则得到每一位专家的计算权重w r,根据自身判断对事件的失效概率范围给出定义并给出信心指数,在失效概率范围中填入认为的概率区间[L ij,Rij],在信心指数中填出做出判断的信心程度k ij(0 (2)令Δij=Rij-L ij,可以求出专家对于故障概率判断的范围。 (3)取m ij=Δij/2,即专家i对于基本事件j发生概率累计结果的贡献为 (4)通过加权以及利用信心指数修正可以求得第j个事件的发生概率,这个结果将是一个等腰三角形模糊数 通过历史数据以及基于专家调查可以得到部件的模糊故障率,如表3所示。现假设部件出现故障状态为0.5,即部分失效的故障率与故障状态为1,即完全故障的模糊故障率相同。 表3 汽车起重机变幅机构模糊故障率Tab.3 Fuzzy failure rate of luffing mechanism of truck crane 利用式(3)以及表1可得到中间事件的故障发生概率分别为 同理,可求得其他事件中间事件的发生概率,继而可以得到顶事件T的模糊可能性: 利用前面介绍的概率重要度与关键重要度的计算公式,将模糊故障概率的均值作为故障概率可以求出各底事件的概率重要度以及关键重要度,如表4所示。 表4 各事件的概率重要度及关键重要度Tab.4 Probabilistic and critical importance of events 通过对比各个底事件相对于顶事件故障状态为0.5和1的状态重要度,可以找出对于系统影响发生故障概率较大的环节,有必要提高其中关键重要度大的事件,如:x1(液压泵密封件损坏)、x5(油液混油空气)、x10(导轨润滑不良)、x15(液压缸密封件失效)、x16(液压缸内磨损)的可靠性,对于提升系统的可靠性有明显效果。 利用贝叶斯网络能够反向推理的特性,可以在已知顶事件的故障状态下求出底事件的后验概率,后验概率的求出有助于系统出现故障之后更快速的找出问题所在。通过计算当顶事件发生故障时,x12(液压缸内存有气体)、x14(活塞杆与缸体同轴度差)、x15(液压缸密封件失效)等后验概率较大,可以按照其概率对底事件进行排查,提高底事件的可靠性、进行可靠性优化从而达到提高系统可靠性的目的。 (1)通过将BN贝叶斯网络与T-S模糊故障树进行融合,克服了T-S模糊故障树计算繁琐、不能双向推理的不足,解决了传统BN贝叶斯网络对于复杂系统构建困难与不能描述事件的模糊逻辑关系的难题。 (2)将BN贝叶斯网络与T-S模糊故障树2种可靠性计算方法优势互补,利用模糊数描述事件的可靠性,正向推理通过计算可以得到顶事件的发生概率以及底事件的重要度,反向推理又能得到系统故障状态下底事件的后验概率,BN贝叶斯网络与T-S模糊故障树的结合获得了一种应用范围更广的可靠性评估方法。 (3)以某汽车起重机变幅机构为工程例,利用基于贝叶斯网络和T-S模糊故障树的可靠性评估方法对其进行评估,建立了评估模型,计算出系统的可靠性、底事件的重要度以及系统故障状态下的后验概率,计算结果符合实际,为系统可靠性的提升以及故障诊断提供了依据。


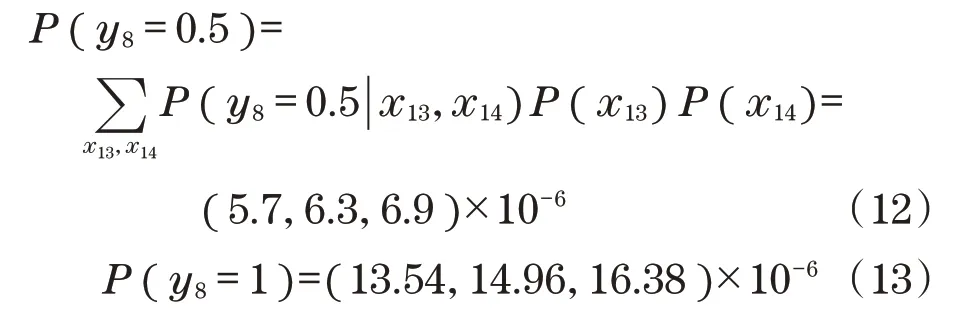

4 结论

